Применение производной в биологии, химии, статистике.

Применение производной  в  биологии,  химии,  статистике.

"Просто знать - ещё не всё, знания нужно использовать".

Гете.

В исторических данных формула производной встречается ещё в 15 веке. Великий итальянский математик Тартальи, рассматривая и развивая вопрос - на сколько зависит дальность полёта снаряда от наклона орудия - применяет её в своих трудах.  Метод дифференциального исчисления был описан  в XVII и XVIII вв. И. Ньютоном и Г.В. Лейбницем. Они пришли к открытию дифференциального исчисления при решении задач о скорости движения материальной точки в данный момент времени и проведении касательной к произвольной линии, объяснив этим ее геометрический смысл. Производная и различные изложения с её применением стали встречаться в работах Галилео Галилея, Декарта, французского математика Роберваля и англичанина Грегори, Большой вклад по изучению производной внесли такие умы, как Лопиталь, Бернулли, Лангранж и др.

Дифференциальное исчисление - это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.

1.    Применение производной в химии и биологии

Производная характеризует   в биологии – скорость размножения колонии микроорганизмов, в химии – скорость химической реакции.   

   Пусть зависимость между числом особей популяции микроорганизмов у и временем t её размножения задана уравнением: у = x(t).

Пусть ∆t - промежуток времени от некоторого начального значения t до t+∆t. Тогда у + ∆у = x(t+∆t)- новое значение численности популяции, соответствующее моменту t+∆t, а  ∆y + x(t + ∆t  )- x(t)  -  изменение числа особей организмов. Отношение является средней скоростью размножения или, как принято говорить, средней производительностью жизнедеятельности популяции. Вычисляя , получаем y΄ = P(t) = x΄ (t), или производительность жизнедеятельности популяции в момент времени  t.

З а д а ч а 1.

  Пусть популяция бактерий в момент t (с) насчитывает x(t) особей.   x(t) = 3000 + 100t.²                             Найти скорость роста популяции:
а) в произвольный момент t,   
б) в момент t = 1 c.

    Решение:

   P = x’(t) = 200t;

   P(1) = 200 (k/с).

   Ответ:  200t; 200 k/с.

З а д а ч а 2.

Пусть дана функция p=p(t),где p-количество некоторого вещества, вступившего в химическую реакцию в момент времени t. Приращению времени ∆t будет соответствовать приращение ∆p  величины  p. Отношение ∆p/∆t- есть средняя скорость химической реакции за промежуток времени ∆t. Предел этого отношения при стремлении t∆ к нулю - есть скорость химической реакции в данный момент времени .

                     v(t) = p΄(t)

Скорость химической   реакции – один из решающих  факторов, который нужно            учитывать во многих областях   научно-производственной деятельности. Например, инженерам-технологам при определении эффективности химических производств, химикам, разрабатывающим препараты для медицины и сельского хозяйства, а также врачам и агрономам, использующим эти препараты для лечения людей и для внесения их в почву. Одни реакции проходят практически мгновенно, другие идут очень медленно. В реальной жизни для решения производственных задач, в медицинской, сельскохозяйственной и химической промышленности важно знать скорости реакций химических веществ.

З а д а ч а 3.

     Пусть количество вещества, вступившего в химическую реакцию задается зависимостью:    р(t) =  + 3t –3 (моль).
Найти скорость химической реакции через 3 секунды.

      Решение:

      v (t) = p΄(t);
      v (t) = t + 3;
      v (3) = 3+3 = 6.(моль/c)

     Ответ: 6 моль/с.

З а д а ч а 4.

З а д а ч а 5.

З а д а ч а 6.

2.    Производная в географии.

          Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t),   N΄(t) = N(t).   Модель Мальтуса неплохо действовала  для описания численности населения  США с 1790 по 1860 годы.  Ныне эта модель  в большинстве стран не действует.

         Выведем формулу для вычисления численности населения на ограниченной территории в  момент времени t.

         Пусть у = у(t)- численность населения.

         Рассмотрим прирост населения за  Dt = t-t₀

         Dy = k y Dt, где  к = к_р – к_с –коэффициент прироста (к_р – коэффициент рождаемости,

         к_с – коэффициент смертности)

           = k y

         При Dt®0 получим  у΄ =

                                у΄= к у

З а д а ч а  7

3.Производная в строительстве

З а д а ч а 8

При монтаже промышленных и сельскохозяйственных зданий небольшой высоты  широко используются автомобильные краны. Для правильного  выбора крана необходимо знать многие исходные данные о сооружаемом объекте. В частности, габаритные данные объекта позволяют заранее определить требуемую длину стрелы крана. Рассмотрим эту задачу. Вывести формулу для определения длины стрелы автомобильного крана, с помощью  которого можно построить здание высоты Н и  ширины 2l c плоской крышей.

Решение: Так как автомобильный кран может перемещаться вокруг всего здания, то крюк его крана достанет до любой точки здания, если он достанет  до середины крыши (имеется в виду середина по ширине).

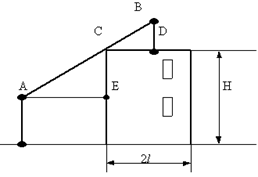
Рассмотрим кран, который находится в точке О, подает деталь на середину крыши. Пусть угол наклона стрелы при этом составляет . Тогда BC=  =; AC =  = , где h = АО – высота подвеса стрелы крана. В таком случае длина стрелы крана    l =   +     (1)

Из формулы (1) видно, что для совершения указанной работы краном, установленным в другой точке (ближе к зданию или дальше от него), потребуется кран с другой длиной стрелы, поскольку при таком перемещении меняется угол . Определим наивыгоднейшее место установки крана, т.е. такое место, с которого заданная работа может быть выполнена краном с наименьшей длиной стрелы. Для  этого достаточно определить, при каком  из промежутка (0;) функция l принимает наименьшее значение. Найдем производную функции: l΄() =  =  ().

Производная обращается в нуль лишь в одной точке ₀= arctgи функция l достигает своего наименьшего значения при ₀= arctg. Найдя из полученной формулы значение ₀ и подставив его в формулу (1), мы и получим наименьшее возможное значение стрелы. Эти формулы и используются на практике.

З а д а ч а 9: "Облицовка".

Заготовленной плиткой нужно облицевать 6000 кв. м боковых стенок и дна желоба прямоугольного поперечного сечения длиной 1000 м. Каковы должны быть размеры сечения, чтобы пропускная способность желоба была наибольшей?

З а д а ч а 10: "Максимальный слив"

Необходимо построить открытый желоб прямоугольного сечения для стока воды. Длина периметра поперечного сечения желоба должна равняться 6 м. Какой высоты должны быть стенки желоба, чтобы получился максимальный слив?

З а д а ч а 11: "Стоянка автомобилей".

Для стоянки машин выделили площадку прямоугольной формы, примыкающую одной стороной к стене здания. Площадку обнесли с трех сторон металлической сеткой длиной 200 м, и площадь ее при этом оказалась наибольшей. Каковы размеры площадки?

4.Производная в экстремальных ситуациях и в жизни.

З а д а ч а 12: 

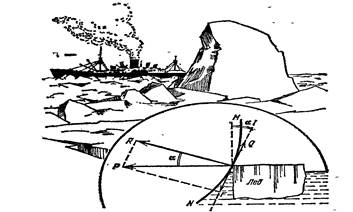
Пароход “Челюскин” в феврале 1934 года успешно прошел весь северный морской путь, но в Беринговом проливе оказался зажатым во льдах. Льды унесли “Челюскин” на север и раздавили.

Вот описание катастрофы: “Крепкий металл корпуса поддался не сразу, – сообщал по радио начальник экспедиции О.Ю. Шмидт. – Видно было, как льдина вдавливается в борт, и как над ней листы обшивки пучатся, изгибаясь наружу.

Лед продолжал медленное, но неотразимое наступление. Вспученные железные листы обшивки корпуса разорвались по шву. С треском летели заклепки. В одно мгновение левый борт парохода был оторван от носового трюма до кормового конца палубы…”

Почему произошла катастрофа?

Сила Р давления льда разлагается на две: F и R. R – перпендикулярна к борту, F – направлена по касательной. Угол между P и R – a – угол наклона борта к вертикали.

Q – сила трения льда о борт.

Q = 0,2 R (0,2 – коэффициент трения).

Если Q < F, то F увлекает напирающий лед под воду, лед не причиняет вреда, если Q > F, то трение мешает скольжению льдины, и лед может смять и продавить борт.

0,2R < R tg a , tg a > 0,2

Q < F, если a > 11⁰.

Наклон бортов корабля к вертикали под углом a > 11⁰ обеспечивает безопасное плавание во льдах.

З а д а ч а 13: 

Лестница длиной 5м приставлена к стене таким образом, что верхний  ее  конец

находится на  высоте  4м.  В  некоторый  момент  времени  лестница  начинает

падать,  при  этом  верхний  конец  приближается  к  поверхности   земли   с

постоянным ускорением      2 м/с2. С  какой  скоростью  удаляется  от  стены

нижний конец лестницы в тот момент, когда верхний конец находится на  высоте

2м?

З а д а ч а 14.

Из прямоугольного листа жести размером 25 х 40 см надо изготовит открытую коробку наибольшего объема. Для изготовления коробки надо вырезать         квадратные уголки. В зависимости от длины  вырезаемого квадрата получаются коробки, имеющие различные объемы.  Поэтому  необходимо рассчитать размеры  вырезаемых квадратов, при которых коробка имеет  наибольший объем.

Решение. Обозначим сторону вырезаемых по углам квадратов через х. Дном коробки является  прямоугольник, стороны которого равны а = 25 – 2х и в = 40 – 2х. Высота коробки равна х. Следовательно, объем коробки равен V = (25 – 2х)(40 – 2х)х, т.е. является функцией от переменной х.

у = (25 – 2х)(40 – 2х)х = 4х³ – 130х² + 1000х.

             Область определения этой функции промежуток (0; 12,5).

             Найдем экстремумы этой функции.

             у' = (4х³ – 130х² + 1000х)' = 12х² – 260х + 1000

            12х² – 260х + 1000 = 0

           Критические точки функции х₁ 16,7 – не входит в область определения функции.

             х₂ = 5

          Определим знак производной в промежутках

            (0; 5) у' > 0
            (5; 12,5) у' < 0

           Так как при переходе через точку х = 5 производная меняет знак с плюса на минус, то при

            х = 5 функция у = (25 – 2х)(40 – 2х)х = 4х³ – 130х² + 1000х имеет максимум.

           Следовательно, коробка будет иметь наибольший объем при вырезании квадратов со    

           стороной 5 см. Найдем объем полученной при этом коробки:

             V(5) = 2250см³.

З а д а ч а 15.

Высота снежка, брошенного вертикально вверх со скоростью U₀ с начальной высоты h_0, меняется по закону h =h₀+U₀*t-gt²/2, где g » 10м/c – ускорение силы тяжести. Покажите, что энергия камня Е=тv²/ 2 + mgh, где т – масса снежка, не зависит от времени.

Решение:

V (t) = h ^/ (t) = V₀ – gt                     E = m/2 (V₀ - gt)² + mg(h₀ + V₀t – gt²/2) = mV₀²/2 + mgh_0.

Решить самостоятельно.

Задача 1.  Рост бактерий в биологии выражается формулой

Z (t) = 100 +  , где t – время в часах.

Определить скорость размножения бактерий V(t)  за 0,5 часа, если  V (t) = Z ʹ (t).

Задача 2.  Пусть популяции бактерий в момент времени t сек. насчитывают Х особей.   Х(t) = 3000 + 100t²

Найти скорость роста популяции в момент времени 3 сек.

Задача 3. Зависимость урожайности некоторых культур зависит от количества внесенных удобрений на 1 га площади выражается формулой Z(x) = 5 + 0,2x -3,,, (x в кг). Вычислить, при каком минимальном количестве внесенных удобрений на 1 га площади начнется рост урожайности культур?

Задача 4.  Пусть количество вещества, вступившего в химическую реакцию в зависимости от времени задается формулой

Р ( t) =  + 3t -3 (моль). Найти скорость химической реакции V(t) через 3 секунды, если скорость – это производная от концентрации реагирующих веществ по времени.

Задача 5. Расход природных ресурсов Q(t) вычисляется по формуле Q(t) = -  , где t – одно  десятилетие. Вычислить коэффициент расхода ресурсов K(t) через 2 десятилетия, если

K(t) = Q ʹ(t) .(  ln2  ).

Задача 6.  Вычислить прирост населения  Р (t) на некоторой территории, численность населения  которой задана формулой

N = 4,2 t²- 79.4 t + 54,78 (тыс.чел.), где t – интервал времени в годах, если прирост Р (t) = N ʹ (t) , а интервал времени равен 10 лет.

Задача 7.   Рост населения описывается формулой

U(x) = 360 x +900. Рост производства молочной продукции задается формулой V(x) = 160x +900, x – время в годах. Найдите скорость роста производства молочной продукции на душу населения через 10 лет.

( Результат округлить до сотых и дать в %).

Задача 8.  Успеваемость в классе в процентах от посещаемости находится в зависимости y = x³ -3,5 x² + 9 ln x, где х – посещаемость уроков по предмету в неделях. Найти рост успеваемости R(x) по предмету в процентах через 2 недели, если R(x) = yʹ (x).

Задача 9.  Автомобиль приближается к мосту со скоростью 72 км/час. У моста висит дорожный знак «36 км/час». За 7 секунд до въезда на мост водитель нажал на тормоз. С разрешаемой ли скоростью автомобиль въехал на мост, если тормозной путь определяется формулой

S(t) = 20t – t² (м).    ( V(t) = S ʹ(t) ).

Задача 10. Опытным путем установлена функция спроса и предложения в зависимости от цены товара: G (p) =  ,

где р – цена товара в рублях. Найти эластичность по спросу и предложению  Z (p) = G ʹ (p), если равновесная цена р = 2

 ( равновесная цена – это когда спрос и предложение уравновешены). 

Вывод: При вычислении получается  ответ 0,08. Это означает, что при увеличении цены на 1 % спрос уменьшается на 8%.

Ответы на задачи.

1.    48 бактерий.

2.   Скорость 600 бак\сек.

3.    56,75 кг на1 га.

4.   Скорость химической реакции 6 моль\сек.

5.   Коэффициент расхода природных ресурсов равен – 0,4.

6.       Прирост населения 4,6 тыс.чел.

7.        9 %.

8.          Успеваемость вырастет на 2,5 %.

9.  V = 6 м\сек., а 36 км\ч = 10 с\сек.Вьехал с разрешаемой скоростью

10.                 g ʹ(2) = 0,08 При уменьшении цены на 1 % спрос уменьшается на 8%.