проект красота пропорции

МОУ ОредежскаяСОШ»

                               ПРОЕКТ

                                                                               Выполнили учащиеся 6а кл

                                                                              Руководитель Степанова Е.С.

2024г.

СОДЕРЖАНИЕ

1.Введение………………………………………………….стр.3

  а) Актуализация…………………...…………………… ..стр.3

  б) Проблема…………………………...………………… стр.3

  в) Гипотеза…………………………...………………….. стр.3

  г) Цель…………………………………………………….стр.3

. д) Задачи………………………………………………….стр.3

2. Основное содержание. «Гармония и пропорция.»........стр.4

  а) Происхождение пропорции, золотого сечения...........стр.4

  б) Золотая пропорция и архитектура.............................   стр5

  в)  Золотое сечение и скульптура......................................стр6

  г)  Золотое сечение в живой природе...............................стр.8

  г)  Музыкальная гармония  пропорции............................стр.9

  д) Золотое сечение и живопись........................................ стр10

3. Заключение.......................................................................стр.13

Список использованной литературы..................................стр.13  

Введение.

а) Актуализация.

  Отрезок можно разделить на две части бесконечным множеством способов. В частности, можно разделить так, чтобы отношение всего отрезка к его большей части равнялось отношению большей части к меньшей. Такое деление  отрезка со времен древних греков называется делением отрезка в крайнем и среднем отношении. Чем же интересно такое деление отрезка? Почему  оно  привлекало строителей древнего мира?

б) Проблема.

  Какую роль играет  божественная пропорция в нашей жизни?

Есть ли взаимосвязь между пропорцией и гармонией?

в) Гипотеза.

  Мы предполагаем, что пропорция играет важную роль в нашей жизни, что она влияет на красоту  и гармонию нас окружающего.

г) Цель.

Воспитание интереса к предмету через умение видеть прекрасное в пропорциональности окружающего мира.

д) Задачи.

Выяснить роль пропорции.

Проанализировать области, в которых встречается пропорция.

Привить навыки применения божественной пропорции на уроках рисования.

Выяснить тайну золотого сечения.

е) Ожидаемые результаты.

Будут рассмотрены применение золотого сечения в архитектуре, скульптуре, живописи.

Будет выявлено, что общего между пропорцией и музыкой.

Будет  раскрыта тайна золотого сечения

Будет проведен психологический тест.

2. Основное содержание.

ГАРМОНИЯ И ПРОПОРЦИЯ

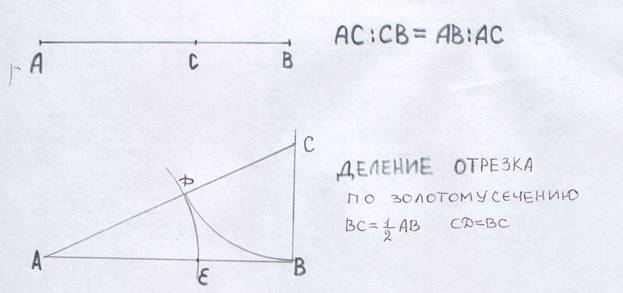а) Происхождение пропорции, золотого сечения.

 Ученые в Древней Греции не признавали дробных чисел и из-за этого у них возникали затруднения с измерением величин. Пришлось греческим ученым  придумать способ, как обходиться в науке без того, чтобы выражать длины, площади и объемы числами. Так было создано учение об отношениях величин, о равенстве таких отношений. Равенство двух отношений стали называть латинским словом «пропорция». Деление  отрезка в среднем и крайнем отношении часто использовалось в искусстве, что дало повод математику 16в., другу известного художника Леонардо да Винчи монаху Луке Пачоли назвать такое деление отрезка божественной, великолепной пропорцией. По поводу этой пропорции он употреблял много хвалебных слов, но в истории утвердилось два варианта: золотая пропорция, или золотое сечение.  Золотое сечение - это такое деление отрезка на две неравные части, при котором длина большей части  относится к меньшей, как длина всего отрезка к длине большей части.

Для практических целей  часто используют приближенные значения 0,618 и 0,38.

 Принято считать, что понятие золотого деления ввел в научный обиход Пифагор (6 в до н.э.). Свое знание он позаимствовал у египтян и вавилонян. Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта, украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались этим соотношением. В рельефе из храма фараона Сети 1 в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. При раскопках  древнегреческого храма Парфенона обнаружены циркули, которыми пользовались архитекторы и скульптуры античного мира. В эпоху Возрождения усиливается интерес к золотому делению среди ученых, художников. Монах Лука Пачоли среди достоинств золотой пропорции не

преминул назвать  ее «божественной суть» как выражение божественного триединства бог сын (малый отрезок), бог отец (большой отрезок), бог дух святого (весь отрезок). Леонардо да Винчи назвал ее «золотым сечением»

б) Золотое сечение в  архитектуре.

 В искусстве пропорциями обычно называют соотношение величин элементов художественного произведения, а также отдельных элементов и всего произведения в целом. Различают архитектурные пропорции и пропорции, используемые для изображения человеческого тела и лица.        Самые простые пропорции основаны на кратких и целочисленных отношениях, например 1:2, 3:4 и т.д.. Но уже с древности широко распространились системы пропорционирования, приводящие к иррациональным отношениям.  Самым популярным из них является  золотое сечение.

    На прямоугольники, в которых стороны соотносятся приблизительно как 1,6:1 (8:5), обратили очень давно. Золотое сечение многократно встречается в

древнем сооружении храме Парфенона в Афинах.

 Архитектура Парфенона имеет 8 колонн по коротким сторонам и 17 по длинным. Если произвести деление Парфенона по  «золотому сечению», т получим те или иные выступы фасада. Так, приняв за 1 ширину торцевого фасада здания, можно получить геометрическую прогрессию, состоящую из восьми членов: расстояние между второй и седьмой колоннами равно ф, третьей и шестой - ф, четвертой и пятой - ф. Аналогичные закономерности есть и в построении здания по высоте. Объединив их, получается прогрессия.

Отношение высоты здания к его длине равно 0,618.

.

Построение золотого прямоугольника с помощью циркуля и линейки.

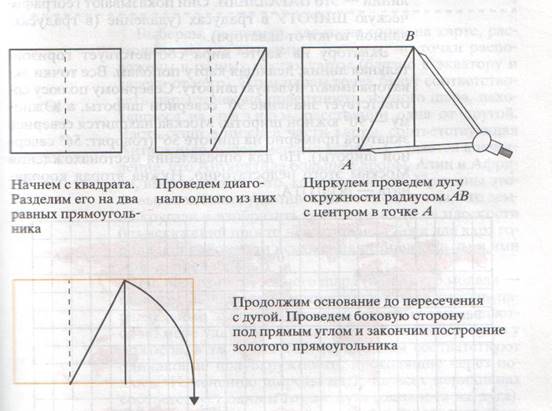в) Золотое сечение в скульптуре.

Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей. Еще в древности основу скульптуры составляла теория пропорций. В своих творениях древнегреческие мастера  исходили из пропорций, которые видели, прежде всего, в пропорциях человеческого тела

В одном из чудес света - статуи Зевса Олимпийского использовано «золотое сечение».

Скульптор и теоретик искусства Поликлет (вторая  половина 5 в. до н.э).                                                                                        в своем трактате «Канон» стремился установить законы пропорциональности человеческого тела. Теория пропорций ярко воплотилась в статуе  «Дорифор» - копьеносец, которую он изваял в строгом соответствии всех  частей. Так пупок делит высоту статуи в отношении золотого сечения.

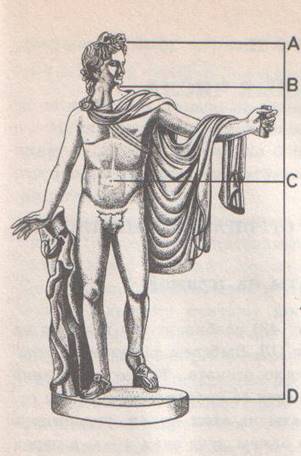
                                                                          Знаменитая скульптура Аполлона

                                                      Бельведерского разделена в таком отношении.

                                                       Точка С делит отрезок АД, точка В делит                                                                                                                                                                            отрезок АС.                                   отрезок АС.

   Во времена Возрождения для проверки «закона гармонии »                     измеряли античные статуи, полтора века назад пропорции «золотого сечения» проверяли, соотнося  длину ноги и туловища  гвардейских солдат - все совершенно точно.

 Наиболее  распространено пропорционирование на основе золотого сечения при возведении памятников. Общая высота памятника обычно относится к высоте фигуры, как высота фигуры - к размеру постамента (или наоборот, если  постамент выше, чем фигура).

    Золотое сечение можно увидеть и в пентаграмме - так называли греки звездчатый пятиугольник ( от слова «пенте» - пять) Он служил символом Пифагорейского союза - религиозной секты и научной школы во главе с Пифагором.(около 580-500 до н.э.). По их теории, в основу мирового порядка положены числа. Мир, считали они, состоит из противоположностей, а

гармония приводит противоположности к единству. Гармония же заключается в числовых отношениях. Пифагорейцы приписывали числам различные свойства.  Так, четные числа они называли женскими, нечетные (кроме 1) - мужскими. Число пять - как сумма первого женского числа (2) и первого мужского (3) - считалось символом любви. Отсюда такое внимание к пентаграмме, имеющей 5 углов.

Стороны пентаграммы, пересекаясь, образуют снова правильный пятиугольник, в котором пересечение диагоналей дает новую пентаграмму, а в пересечении ее сторон снова получается правильный пятиугольник. И так до бесконечности.  Стороны пентаграммы, пересекаясь, делят друг друга на отрезки, длины которых образуют золотую пропорцию.

в) Золотое сечение в природе.

 Золотая пропорция - символ взаимодействия  двух физических сил: тяготения и инерции. Поскольку отношение большей части целого к самому целому выражает основные моменты живого роста: стремительный взлет

легкого юного побега до зрелости и замедленный рост «по инерции» до момента цветения, когда достигшее полной силы растение готовится  дать жизнь новому побегу.

  В 1850 г. немецкий ученый А. Цейзинг открыл так называемый закон угла, согласно которому средняя величина углового отклонения  ветки растения  равна  примерно 138°. Величина среднего углового отклонения ветки соответствует меньшей из двух частей, на которые делится полный угол при золотом сечении.                                                   

На листьях герани и клена можно составить золотое отношение.

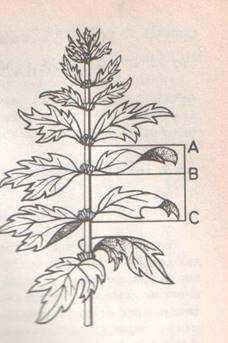                                                         Рассматривая положение листьев                                                 

                                                                         на общем стебле растений, можно                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                               заметить, что между каждыми двумя                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                           

                                                                       парами листьев (А и С) третья  

                                                  расположена в месте золотого                                                                                    сечения (точка В).

.Представление о золотом сечении в природе будет неполным, если не сказать о спирали. Рассмотрим расположение семечек в корзине подсолнуха. Они выстраиваются вдоль спиралей, которые закручиваются как слева направо, так и справа налево. В одну сторону закручено 13 спиралей, в

другую -21. В более крупных соцветиях подсолнечника число соответствующих спиралей 21 и 34 или 34 и 55. Похожее спиральное расположение наблюдается у чешуек сосновых шишек или ячеек ананаса.

  13/21=0,619..., 34/55=0,618..

По такой спирали свернуты раковины многих улиток и моллюсков, та же спираль встречается в соцветиях растений, даже пауки, сплетая паутину, закручивают нити вокруг центра по спирали. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. В ящерице с первого взгляда улавливаются приятные для глаз пропорции - длина ее хвоста так относится к длине остального тела, как 62 к 38.  

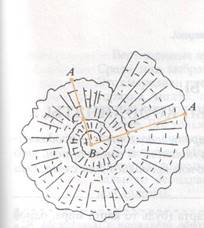На рисунке  изображена раковина:

точка  С делит  отрезок АВ приблизительно

в золотом отношении

г) Музыкальная гармония пропорции.

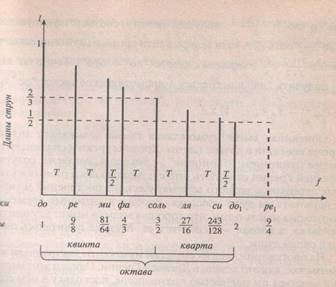
 При изучении музыкальных закономерностей Пифагор установил, что две струны дают приятное для слуха совместное звучание (консонанс), когда их длины относятся, как 1:2, 2:3 или 3:4. Если взять четыре струны, то длина первой будет в два раза больше последней (их совместное звучание - октава). Длина третьей струны будет относиться к длине первой, как 2:3 (интервал - квинта), и отношение второй к первой равно 3:4, что определяет еще один интервал - кварту. Длины четырех  струн, дающих консонансы,

должны быть 6,8, 9, 12.

В Древней Греции считалось, что

с помощью гамм разных музыкальных

оттенков и разного математического

построения можно воздействовать

на душу человека.

д) Золотое сечение в живописи.

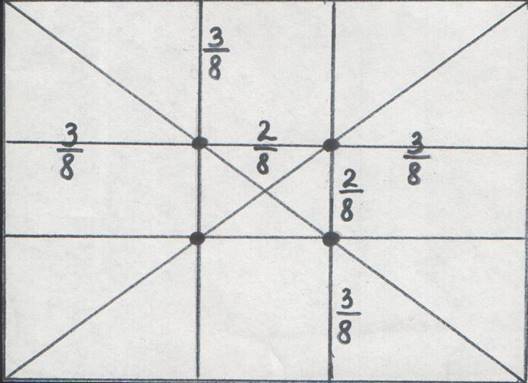
Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно притягивающие наше внимание, так называемые зрительные центры. Таких точек всего 4 и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости. Это «золотое сечение»  картины. Чтобы привлечь внимание к главному элементу

фотографии, надо совместить этот элемент с одним из зрительных центров.

10

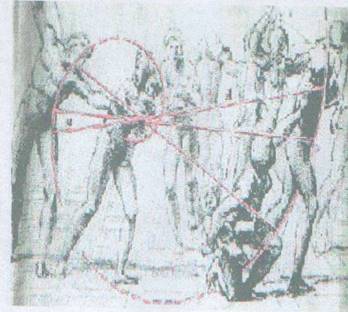
Золотая спираль в картине Рафаэля

«Избиение младенца»

   В картине сочетаются динамизм и гармония.

Этому сочетанию способствует выбор

 золотой спирали за композиционную основу

 рисунка   

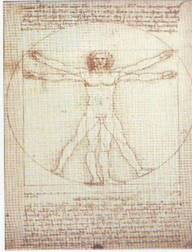
Золотое сечение в картине

Леонардо да Винчи «Джоконда»

Портрет Моны Лизы  привлекает тем,

что композиция рисунка построена

на «золотых треугольниках «

(треугольниках, являющихся кусочками

правильного звездчатого пятиугольника)

 Картина   И. И.  Шишкина «Корабельный лес»

 Сосна на первом плане делит длину  картину по золотому сечению. Справа от сосны - пригорок. Он делит по золотому сечению правую часть картины по горизонтали.

Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия, в соответствии с замыслом художника. Геометрические фигуры, в которых есть элементы, связанные друг с другом золотой пропорцией, большинству людей кажутся красивыми.

 Тайна золотого сечения

Оказывается, возбуждение струны в точке, делящей ее в отношении золотого сечения на частоте близкой к основной гармонике, не вызывает колебание струны, то есть точка золотого сечения - это точка компенсации, демпфирования. На летательных аппаратах с электромагнитными источниками энергии используются  прямоугольные ячейки  с пропорцией золотого сечения. Это позволяет сориентировать электромагнитные колебания по нужному направлению (вертикально или горизонтально).

ЗАКЛЮЧЕНИЕ.

    Подводя итоги своей работы, мы можем сказать, что цель нашего проекта достигнута. Мы проследили, какую огромную роль  играет пропорция в скульптуре, живописи, природе, музыке. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке.

    Человеческие представления о красивом формируются явно под влиянием того, какие воплощения порядка и гармонии человек видит в живой природе. А природа, как известно, любит повторения. В различных своих творениях, казалось бы, очень далеких друг от друга, она может использовать одни и те же принципы. Золотое сечение - один из основополагающих принципов природы. Кстати, золотое сечение - предпочтительное во многих случаях, но, однако, не единственное пропорциональное отношение, зрительно воспринимаемое как красивое.

   Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета. Принцип золотого сечения - высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике, природе.

Список использованной литературы.

1. А. И. Азевич. « Двадцать уроков гармонии». - М.: Школа-Пресс,1998. - 160с.: ил.

2. Депман И.Я. Виленкин Н.Я. « За страницами учебника математики». Пособие для учащихся 5-6кл. ср.шк. - М.: Просвещение, 1989. - 287 с.: ил.

3. Математика: Учеб, для 6 кл. средней  школы./Н. Я. Виленкин. - 2-е изд. - М.: Мнемозина, 2007. - 287с.: ил.

4. Шарыгин И.Ф. «Наглядная геометрия» 5-6кл.: Пособие для общеобразовательных учебных заведений. - М.: Дрофа, 1998. - 192 с.: ил.

5. Энциклопедический словарь юного художника./Сост. Н.И. Платонова. - М.: Педагогика, 1983. - 416с., ил.