ПЗ Системы счисления

Практическое занятие 4-6

Тема: «Системы счисления»

Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.

Все системы счисления делятся на позиционные и непозиционные.

Непозиционными системами являются такие системы счисления, в которых каждый символ сохраняет свое значение независимо от места его положения в числе.

Примером непозиционной системы счисления является римская система. К недостаткам таких систем относятся наличие большого количества знаков и сложность выполнения арифметических операций.

Система счисления называется позиционной,   если одна и та же цифра имеет различное значение,   определяющееся позицией цифры в последовательности цифр, изображающей число.  Это значение меняется в однозначной зависимости от позиции, занимаемой цифрой, по некоторому закону.

Примером позиционной системы счисления является десятичная система, используемая в повседневной жизни.

Количество p различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основанием системы счисления ­ "p".

В десятичной системе используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; эта система имеет основанием число десять.

Любое число N в позиционной системе счисления с основанием p может быть представлено в виде полинома от основания p:

N = a_np ⁿ+a_n-­1p ^n-­1+ ... +a₁p+a₀+a-_­1p^-1+a_­-2p^-­2+ …

здесь N ­ число, a_j ­ коэффициенты (цифры числа), p ­ основание системы счисления (p>1).

Принято представлять числа в виде последовательности цифр:

N = a_na_n-­1 ... a₁a₀ . a_­-1a_-­2 ...

В этой последовательности точка отделяет целую часть числа от дробной (коэффициенты при положительных степенях,   включая нуль,   от коэффициентов при отрицательных степенях).   Точка опускается,   если нет отрицательных степеней   (число целое).

В ЭВМ применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную.

В аппаратной основе ЭВМ лежат двухпозиционные элементы,   которые могут находиться только в двух состояниях; одно из них обозначается 0, а другое ­ 1. Поэтому основной системой счисления применяемой в ЭВМ является двоичная система.

Двоичная система счисления. Используется две цифры: 0 и 1. В двоичной системе любое число может быть представлено в виде:

N = b_nb_n-­1 ... b₁b₀ . b_-­1b­₂ ...

где b_j либо 0, либо 1.

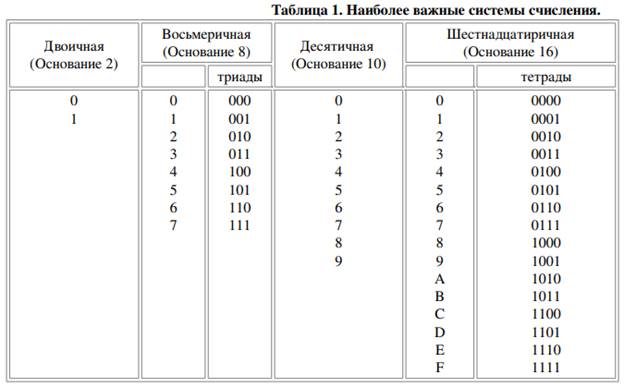
Восьмеричная система счисления. Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употребляется в ЭВМ как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (Таблица 1).

Шестнадцатеричная система счисления. Для изображения чисел употребляются 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр   ­   латинскими буквами:   10­A,   11­B,   12­C,   13­D,   14­E,   15­F.  Шестнадцатеричная система используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада) (Таблица 1).

Перевод чисел из одной системы счисления в другую.

Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы,   из которой число переводится.   Затем подсчитывается значение суммы.

Пример.

а) Перевести 10101101.101₂ "10" с.с.

При одновременном использовании нескольких различных систем счисления основание систем,   к которой относится число,     указывается в виде нижнего индекса.

10101101.101₂ = 1* 2 ⁷+ 0* 2 ⁶+ 1 *2 ⁵+ 0 *2 ⁴+ 1* 2 ₃+ 1* 2 ²+ 0* 2 ¹+ 1 *2 ⁰+ 1 *2 ^-­1+ 0* 2 ^-­2+ 1* 2 ­^-3 =  173.625₁₀

б) Перевести 703.04₈ "10" с.с.

703.04₈ = 7* 8 ²+ 0 *8 ¹+ 3* 8 ⁰+ 0 *8 ^­-1+ 4 *8 ^­-2 = 451.0625₁₀

в) Перевести B2E.4₁₆ "10" с.с.

B2E.4₁₆ =  11* 16²+ 2 *16¹+ 14* 16⁰+ 4* 16­^-1 = 2862.25₁₀

Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится,   до тех пор,   пока не получится частное меньшее этого основания.   Число в новой системе записывается в виде остатков деления,   начиная с последнего.

Пример.

а) Перевести 181₁₀ "8" с.с.

Результат: 181₁₀ = 265₈

б) Перевести 622₁₀ "16" с.с.

Результат: 622₁₀ = 26E₁₆

Перевод правильных дробей из десятичной системы счисления в недесятичную. Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.

Пример.

Перевести 0.3125₁₀ "8" с.с.

Результат: 0.3125₁₀ = 0.24₈

Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная   (иногда периодическая)  дробь.  В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.

Пример.

Перевести 0.65₁₀ "2" с.с. Точность 6 знаков.

Результат: 0.65₁₀ 0.10(1001)₂

Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.

Пример.

Перевести 23.125₁₀ "2" с.с.

1) Переведем целую часть: 2) Переведем дробную часть:

Таким образом:  23₁₀ = 10111₂;

0.125₁₀ = 0.001₂

Результат:  23.125₁₀ = 10111.001₂

Необходимо отметить,   что целые числа остаются целыми,   а правильные дроби   ­ дробями в любой системе счисления.

Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таб. 1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах.

Пример.

а) Перевести 305.4₈ "2" с.с.

б) Перевести 7B2.E₁₆ "2" с.с.

Для перехода от двоичной к восьмеричной   (шестнадцатеричной)   системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.

Пример.

а) Перевести 1101111001.1101₂ "8" с.с.

б) Перевести 11111111011.100111₂ "16" с.с.

Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад. Пример. Перевести 175.24₈ "16" с.с.

Результат: 175.24₈ = 7D.5₁₆

Двоичная арифметика. Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения.

При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда,   если он имеется.   При этом необходимо учитывать,   что   1+1   дают нуль в данном разряде и единицу переноса в следующий.

Пример. Выполнить сложение двоичных чисел: 

а) X=1101, Y=101;

Результат 1101+101=10010.

б) X=1101, Y=101, Z=111;

Результат 1101+101+111=11001.

При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда. Пример. Заданы двоичные числа X=10010 и Y=101. Вычислить X­Y.

Результат 10010 ­ 101=1101.

Умножение двоичных чисел производится по тем же правилам, что и для десятичных с помощью таблиц двоичного умножения и сложения.

Пример. 1001 101=?

Результат 1001 101=101101.

Деление двоичных чисел производится по тем же правилам, что и для десятичных. При этом используются таблицы двоичного умножения и вычитания.

 Пример. 1100.011 : 10.01=?

Результат 1100.011 : 10.01=101.1.

Самостоятельная работа.

Выполнить перевод числа в соответствии с вариантом.

Часть     II. Машинные коды.

Основы машинной арифметики с двоичными числами.

Любая информация (числа, команды, записи и т. п.) представляется в ЭВМ в виде двоичных кодов фиксированной или переменной длины. Отдельные элементы двоичного кода,   имеющие значение   0   или   1,   называют разрядами или битами.   Двоичный код состоящий из 8 разрядов носит название байта. Для записи чисел также используют 32­ разрядный формат (машинное слово), 16­разрядный формат (полуслово) и 64­разрядный формат (двойное слово).

Коды чисел.

В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел.   Использование кодов позволяет свести операцию вычитания чисел к арифметическому сложению кодов этих чисел. Применяются прямой,   обратный и дополнительный коды чисел.   Прямой код используется для представления отрицательных чисел в запоминающем устройстве ЭВМ,   а также при умножении и делении.   Обратный и дополнительный коды используются для замены операции вычитания операцией сложения,   что упрощает устройство арифметического блока ЭВМ.   К кодам выдвигаются следующие требования:

1)   Разряды числа в коде жестко связаны с определенной разрядной сеткой.  

2)   Для записи кода знака в разрядной сетке отводится фиксированный,   строго определенный разряд.

Например, если за основу представления кода взят один байт, то для представления числа будет отведено 7 разрядов, а для записи кода знака один разряд.

Прямой код.  Прямой код двоичного числа совпадает по изображению с записью самого числа.   Значение знакового разряда для положительных чисел равно   0,   а для отрицательных чисел 1.

Знаковым разрядом обычно является крайний разряд в разрядной сетке. В дальнейшем при записи кода знаковый разряд от цифровых условимся отделять запятой. Если количество разрядов кода не указано будем предполагать, что под запись кода выделен один байт.

Пример. В случае, когда для записи кода выделен один байт, для числа +1101 прямой код 0,0001101, для числа ­1101 прямой код 1,0001101.

Обратный код. Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.

Пример.

Особенности сложения чисел в обратном и дополнительном кодах.

При сложении чисел в дополнительном коде возникающая единица переноса в знаковом разряде отбрасывается.

При сложении чисел в обратном коде возникающая единица переноса в знаковом разряде прибавляется к младшему разряду суммы кодов.

Если результат арифметических действий является кодом отрицательного числа, необходимо преобразовать его в прямой код. При этом обратный код преобразуется в прямой заменой цифр во всех разрядах кроме знакового на противоположные. Дополнительный код преобразуется в прямой также,   как и обратный,   с последующим прибавлением единицы к младшему разряду.

Пример

 Сложить двоичные числа X и Y в обратном и дополнительном кодах.

а) X= 111, Y= ­11;

1) Сложим числа, пользуясь правилами двоичной арифметики:

2) Сложим числа, используя коды:

Прямой код                  Сложение в обратном коде             Сложение в дополнительном коде

Так как результат сложения является кодом положительного числа   (знак   0),   то (X+Y)_обр=(X+Y)_доп=(X+Y)_пр.

б) X= ­101,Y= ­11;

1) Сложим числа, пользуясь правилами двоичной арифметики:

2) Сложим числа, используя коды:

Прямой код                      Сложение в обратном коде              Сложение в дополнительном коде

Так как сумма является кодом отрицательного числа (знак 1), то необходимо перевести результаты в прямой код:

Например:

  Здесь   X   и   Y   ­   коды положительных чисел,   но ЭВМ воспринимает результат их сложения как код отрицательного числа   ("1"   в знаковом разряде).  Для обнаружения переполнения разрядной сетки вводятся модифицированные коды.

В модифицированном обратном и модифицированном дополнительном кодах под знак числа отводится не один, а два разряда: "00" соответствует знаку "+", "11" ­ знаку "­". Прямой код Сложение в обратном коде Сложение в дополнительном коде Прямой код Сложение в обратном коде Сложение в дополнительном коде Любая другая комбинация  ("01" или  "10"), получившаяся в знаковых разрядах служит признаком переполнения разрядной сетки. Сложение чисел в модифицированных кодах ничем не отличается от сложения в обычных обратном и дополнительном кодах.

Рассмотрим предыдущий пример, выполнив сложение в модифицированном обратном коде:

Комбинация   "01"   в знаковых разрядах означает,   что произошло переполнение и получившийся результат ­ неверный.

Рассмотрим ещё один пример.   Пример.  Даны два числа:   X=101001   и   Y=   ­11010.  Сложить их в модифицированном дополнительном коде.

1)                Переведем X и Y в модифицированный дополнительный код:

X= +101001

Y= ­011010

2)                Выполним сложение:

Переполнения нет   (в знаковых разрядах   "00"),   поэтому полученный результат   ­ верный (X+Y=1111)

Самостоятельная работа.

Выполнить арифметические действия над числами в соответствии с вариантом.

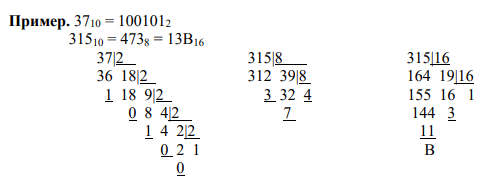
Сложение. В его основе лежит таблица сложения одноразрядных двоичных чисел:

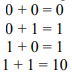
Вычитание. В его основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа(0) большего(1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой:

Умножение. В основе умножения лежит таблица умножения одноразрядных двоичных чисел и происходит по схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на цифры множителя.

Деление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.

Арифметические операции в восьмеричной и шестнадцатеричной системах счисления. Операции выполняются аналогично вычислениям в двоичной системе счисления. Необходимо только помнить, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления. Для проведения арифметических операций над числами, выраженными в различных системах счисления, необходимо предварительно перевести их в одну и ту же систему. Для перевода чисел между системами счисления и выполнения арифметических операций в различных системах счисления, можно использовать стандартную программу Калькулятор.

Практическое занятие 7

Тема: «Системы счисления: Римская система счисления»

Цель работы: научиться переводить числа из непозиционной системы счисления в позиционную и обратно.

1 Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.

2 Непозиционной называется такая система счисления, в которой значение каждого знака не зависит от его положения (места, позиции) в коде числа.

3 В позиционной системе счисления значение цифр зависит от позиции в числе.

4 К непозиционной системе счисления относится и римская, символы алфавита которой и обозначаемое ими количество представлены в таблице.

5 Запись чисел в этой системе счисления осуществляется по следующим правилам:

‒ если цифра слева меньше, чем цифра справа, то левая цифра вычитается из правой;

‒ если цифра справа меньше или равна цифре слева, то эти цифры складываются.

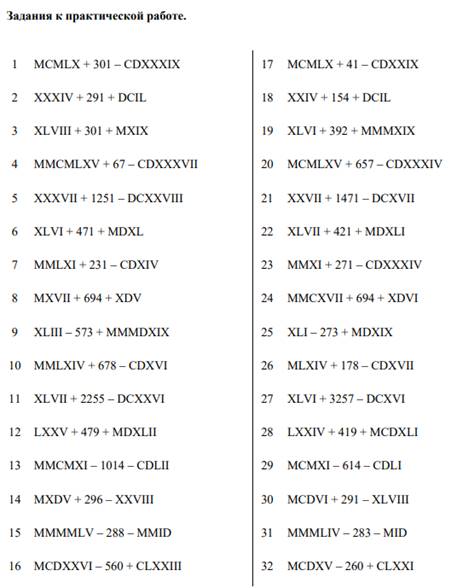
Задание

Исходные данные:

1 Выполнить действия и представить результат с помощью римских и арабских чисел: MCMXXVI + 264 – DXCII

Решение:

а) MCMXXVI = 1000 + 900 + 20 + 6 = 1926

б) DXCII = 500 + 90 + 2 = 592

в) 1926 + 264 – 592 = 1598

г) 1598 = MDXCVIII

ИНСТРУКЦИОННАЯ КАРТА

для проведения практической работы № 2

Тема занятия: Работа с непозиционными системами счисления

Цель выполнения задания: научиться переводить числа из непозиционной системы счисления в позиционную и обратно.

Необходимо знать: основные формулы и правила работы с римскими числами

Необходимо уметь: применять основные формулы и правила работы с римскими числами

Оборудование (приборы, материалы, дидактическое обеспечение): методические рекомендации к выполнению работы; задание и инструкционная карта для проведения практического занятия

Компьютерные программы: компьютерные программы не используются

Теория: для выполнения заданий по данной теме необходимо предварительно изучить теоретические материалы, а также методические рекомендации к выполнению работы

Порядок выполнения задания, методические указания: - ознакомиться с теоретическими положениями по данной теме; - изучить схему решения задач; - выполнить задания практической работы; - сформулировать вывод

Содержание отчета: отчет по практической работе должен содержать: основные определения, рассуждения по решению задач, необходимые вычисления, ответ; вывод по работе

Контрольные вопросы: 1 Что такое система счисления? 2 Что такое непозиционная система счисления? 3 Что такое позиционная система счисления? 4 Какие знаки используются в римской системе счисления? 5 Каковы правила записи римских чисел? 6 Как читать число, если меньшая цифра стоит перед большей? 7 Как читать число, если меньшая цифра стоит после большей?