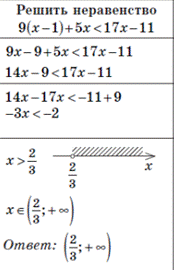Рабочий лист для подготовки к ОГЭ по теме "Неравенства" ( задание 13 и 20)

Рабочий лист по теме "Неравенства" содержит алгоритмы решения линейного, квадратичного неравенства, метод интервалов, подборку заданий ОГЭ для самостоятельного решения, требования к оформлению задания с развёрнутым ответом и образцы оформления решения неравенства второй части ОГЭ.

Линейные неравенства.

1.  Решите неравенство 

1) (-4;+ꝏ)  2) (-ꝏ; -¼) 3) (-¼;+ꝏ) 4) (-ꝏ;-4)

2.  Решите неравенство и определите, на каком рисунке изображено множество его решений.

1)	2)
3)	4)

3.  Решите неравенство и определите, на каком рисунке изображено множество его решений.

1)	2)
3)		4)

4.  Решите неравенство и определите, на каком рисунке изображено множество его решений.

1)	2)
3)	4)

5. При каких значениях a выражение 5a + 9 принимает отрицательные значения?

1)   2)   3)   4)  

6. Решите неравенство

1)  (−4; +∞) 2)  (−12; +∞) 3)  (−∞; −4) 4)  (−∞; −12)

7.  При каких значениях x значение выражения 9x + 7 меньше значения выражения 8x − 3?

1)  x > 4 2)  x < 4 3)  x > − 10 4)  x < − 10

8.  При каких значениях x значение выражения 6х-2 больше значения выражения 7х+8?

1)  x > − 10 2)  x < − 10 3)  x > − 6 4)  x < − 6

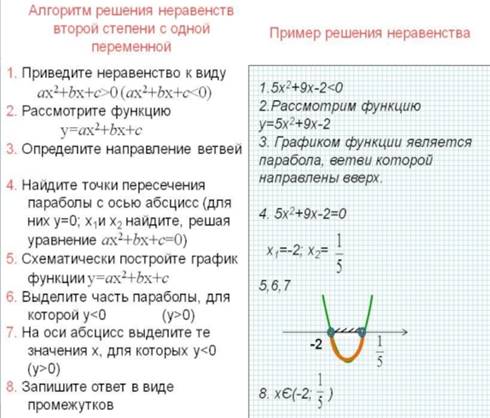
Квадратные неравенства

1.  На каком рисунке изображено множество решений неравенства $x в квадрате минус 4x плюс 3\geqslant0?$

1)		2)
3)	4)

2.  Решение какого из данных неравенств изображено на рисунке?

1)   2)   3)   4)  

3.  Решите неравенство

1)   $левая круглая скобка минус бесконечность ; минус 1 правая квадратная скобка \cup левая квадратная скобка 0; плюс бесконечность правая круглая скобка$ 2)   3)   4)   $левая круглая скобка минус бесконечность ; 0 правая квадратная скобка \cup левая квадратная скобка 1; плюс бесконечность правая круглая скобка$

4.  Решите неравенство

1)   2)   $левая круглая скобка минус бесконечность ; 0 правая круглая скобка \cup левая круглая скобка 4; плюс бесконечность правая круглая скобка$ 3)   4)   $левая круглая скобка минус бесконечность ; 0 правая квадратная скобка \cup левая квадратная скобка 4; плюс бесконечность правая круглая скобка$

5.Решите неравенство

1)   $левая круглая скобка минус бесконечность ; минус 19 правая круглая скобка \cup левая круглая скобка 19; плюс бесконечность правая круглая скобка$ 2)   $левая круглая скобка минус бесконечность ; минус 19 правая квадратная скобка \cup левая квадратная скобка 19; плюс бесконечность правая круглая скобка$ 3)   4)  

6. Укажите неравенство, которое не имеет решений.

1)  x² − 64 ≤ 0 2)  x² + 64 ≥ 0 3)  x² − 64 ≥ 0 4)  x² + 64 ≤ 0

7.  Укажите неравенство, решением которого является любое число.

1)  x² − 15 < 0 2)  x² + 15 > 0 3)  x² + 15 < 0 4)  x² − 15 > 0

8.  На каком из рисунков изображено решение неравенства 

1)	2)
3)	4)

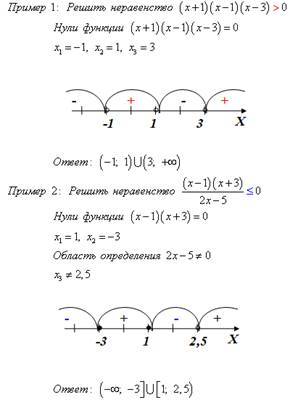Метод интервалов

9. На каком рисунке изображено множество решений неравенства  ?

1)	2)
3)	4)

10.  Решите неравенство:

1)   $левая круглая скобка минус бесконечность ; минус 23 правая круглая скобка \cup левая круглая скобка 0; плюс бесконечность правая круглая скобка$ 2)   $левая круглая скобка минус бесконечность ; минус 23 правая квадратная скобка \cup левая квадратная скобка 0; плюс бесконечность правая круглая скобка$ 3)   4)  

11.  На каком из рисунков изображено решение неравенства

1)		2)
3)	4)

12.  Укажите решение неравенства

1)	2)
3)		4)

Рациональные неравенства

 13. Решите неравенство: На каком из рисунков изображено множество его решений?

1)		2)
3)	4)

14. На каком рисунке изображено множество решений неравенства 

1)	2)
3)		4)

Системы неравенств

Пример 1:

решить систему неравенств 2x−1>3

3x−2<11.

1. Решаем первое неравенство, получаем 2x>4|:2;

x>2.

2. Решаем второе неравенство, получаем 3x<13|:3;

x<13:3;

x<.

3. Полученные промежутки отметим на оси координат.

4. Решение системы неравенств — это пересечение решений неравенств, входящих в систему, т. е. промежуток, на котором оба неравенства имеют решения.

В данном случае получаем ответ: (2;4).

Пример2:

решить двойное неравенство 24<3x<72.

1. Данное неравенство записываем в виде системы неравенств: 24<3x,

3x<72.

2. Из первого неравенства получаем x>8, из второго — x<24.

3. Полученные промежутки отмечаем на координатной прямой.

4. Решение системы (следовательно, и самого двойного неравенства) — (8;24).

15. Решите систему неравенств На каком рисунке изображено множество ее решений?

1)		2)
3)	4)

16.  Решите систему неравенств На каком из рисунков изображено множество ее решений?

1)	2)
3)		4)

17.  Найдите наибольшее значение x, удовлетворяющее системе неравенств

18.  Решите систему неравенств На каком рисунке изображено множество ее решений?

1)		2) система не имеет решений
3)	4)

19. Укажите решение системы неравенств:

1) (7;8)	2)
3)	4)

Задание 20 с развёрнутым ответом.

1.  Решите неравенство 

2.  Решите неравенство

3.  Решите неравенство

4.  Решите неравенство

5.  Решите неравенство

6.  Решите неравенство

7.  Решите неравенство $дробь: числитель: минус 10, знаменатель: левая круглая скобка x минус 3 правая круглая скобка в квадрате минус 5 конец дроби \geqslant0.$

8.  Решите неравенство

9.  Решите неравенство $левая круглая скобка 4x минус 6 правая круглая скобка в квадрате \geqslant левая круглая скобка 6x минус 4 правая круглая скобка в квадрате .$

10.  Решите систему неравенств 

11. Решите систему неравенств $система выражений новая строка дробь: числитель: 10 минус 2x, знаменатель: 3 плюс левая круглая скобка 5 минус 2x правая круглая скобка в квадрате конец дроби \geqslant0, новая строка 2 минус 7x\leqslant14 минус 3x. конец системы$

12.  Решите систему неравенств 

Образец оформления решения неравенства.

Квадратное неравенство.

Важно описать функцию, указать, что графиком является парабола, указать направление её ветвей, найти нули функции, схематично изобразить параболу, проставить знаки +/- или штриховку, записать ответ.

Эксперт вправе снизить баллы, если нет записи о рассматриваемой функции, если при решении квадратного уравнения не записано вычисление дискриминанта и корней уравнения ( если применяем теорему Виета, вычислять дискриминант всё равно надо), если отсутствует схематический график параболы, если не записан ответ ( слово «ответ» должно быть написано).

Применяя метод интервалов, нужно указать это в записи решения: писать «решим методом интервалов». Затем ввести функцию, найти её нули, начертить ось х, расставить нули функции,. записать знаки выражения на каждом промежутке, выписать ответ.

Линейные неравенства. 1.

При каких значениях x значение выражения 9 x + 7 меньше значения выражения 8 x − 3? 1) x > 4 2) x < 4…

Решите неравенство 1) 2) 3) 4) 6

Решите неравенство: 1) 2) 3) 4) 11

Полученные промежутки отметим на оси координат

Задание 20 с развёрнутым ответом

Применяя метод интервалов, нужно указать это в записи решения: писать «решим методом интервалов»

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

09.01.2025