Самостоятельная работа по теме: "Растяжение и сжатие"

Растяжение и сжатие

Содержание

Введение

I. Методические указания к решению задач на прочность по теме «Растяжение-сжатие»

II. Вопросы для самопроверки.

III. Порядок решения типовых задач.

IV. Задания для самостоятельного решения.

Список литературы

 

Введение

Внеаудиторная самостоятельная работа студентов проводится с целью:

-- закрепления, углубления, расширения и систематизации знаний, полученных во время занятий;

-- формирования умений и навыков самостоятельного умственного труда;

-- развития самостоятельности мышления.

В данном пособии представлены методические рекомендации по выполнению внеаудиторной самостоятельной работы студентов по дисциплине « Техническая механика» по теме «Растяжение - сжатие».

Все знания и навыки, полученные студентами при изучении этой темы, найдут применение при расчётах в разделе «Детали механизмов и машин».

Рекомендации состоят из четырёх частей.

Первая включает информационный материал, составленный на основании рабочей программы дисциплины, изучая которую студент получает возможность определить объём необходимого для усвоения материала.

Вторая часть рекомендаций содержит вопросы к информационному материалу и служит для осуществления самоконтроля.

Третья часть представляет собой инструкцию по решению конкретных задач, в которых обращается внимание на последовательность выполнения каких-либо действий, использование рациональных способов решения, применение установленной методики обучения.

В четвёртой предложены задания, требующие переноса известного способа решения задач в аналогичную ситуацию, и ответы к задачам, что позволит студентам осуществить самоконтроль за качеством своего обучения. В случае не подтверждения достоверности ответа, студент обращается за консультацией к преподавателю.

Задания выполняются в тетради для самостоятельной работы.

Выполнение студентом в срок самостоятельной работы приучает к ответственности, исполнительности, аккуратности, воспитывает трудолюбие.

Работа с данными рекомендациями не предполагает усвоение новых знаний, но позволяет студенту углублять ранее полученные на лекциях и практических занятиях знания.

 

I. Методические указания к решению задач по теме: «Растяжение-сжатие»

В результате изучения темы студенты должны:

Знать:

-- методику расчёта задач на прочность

Уметь:

-- строить эпюры нормальных сил и напряжений;

-- выполнять расчёт на прочность и подобрать поперечное сечение стержня.

Растяжением или сжатием называется такой вид деформации, при котором в поперечном сечении стержня возникает один внутренний силовой фактор – продольная сила N.

Величина последней равна алгебраической сумме проекций на продольную ось внешних сил, действующих на отсеченную часть стержня

N=∑ FKZ (1)

Так как величина продольных сил в разных сечениях стержня неодинакова, то строится эпюра продольных сил, т.е. график, показывающий изменения величины продольных сил в сечении стержня по его длине.

Под действием продольных сил в поперечном сечении стержня возникает нормальное напряжение, которое определяется по формуле:

σ =N/А

где А- площадь поперечного сечения стержня.

При решении первой задачи от студента требуется умение строить эпюры продольных сил, нормальных напряжений и определять удлинение или укорочение стержня.

Последовательность построения эпюр продольных сил:

Разбиваем стержень на участки, ограниченные точками приложения сил ( нумерацию участков ведём от незакрепленного конца ).

Используя метод сечений, определяем величину продольных сил в сечении каждого участка.

Выбираем масштаб и строим эпюру продольных сил, т.е. под изображением стержня проводим прямую, параллельную его оси, и от этой прямой проводим перпендикулярные отрезки, соответственно в выбранном масштабе продольным силам (положительное значение откладываем вверх ( или в право ) отрицательное - вниз ( или влево).

Последовательность построения эпюр нормальных напряжений.

Разбиваем стержень на участки, ограниченные точками приложения сил и там, где меняется площадь сечения

Строим эпюру нормальных сил

по формуле 1 определяем нормальные напряжения на каждом участке

По полученным значениям в масштабе строим эпюру нормальных напряжений.

Удлинение ( укорочение ) стержня определяется по формуле Гука .

 

где Е – модуль Юнга ( для стали Е=2·10 5 МПа ).

Удлинение (укорочение) определяется на каждом участке стержня, а затем находят алгебраическую сумму полученных значений. Это будет ∆l стержня. Если ∆l положительна, то брус удлиняется, если ∆l отрицательна, то укорачивается.

При решении ряда задач необходимо ясно представлять смысл условия прочности при растяжении – сжатии, знать, что исходя из условия прочности, можно производить три вида расчётов:

а) проверочный, при котором проверяется выполнено ли условие прочности σ≤ [σ] ( или n≥ [n]);

б) определение допускаемой нагрузки;

в) проектный, при котором определяются необходимые размеры поперечных сечений бруса, обеспечивающие заданную прочность.

Студенты должны также уметь пользоваться в ходе решения всеми необходимыми формулами, расчётными зависимостями и правильно выполнять вычисления.

II. Вопросы для самопроверки

2.1. Как нужно нагрузить прямой брус, чтобы он работал на растяжение - сжатие?

2.2 Как определяется напряжение в любой точке поперечного сечения при растяжении (сжатии)?

2.3. Каков физический смысл модуля продольной упругости Е?

2.4. Что такое допускаемое напряжение и как оно выбирается в зависимости от механических свойств материала?

2.5. Сколько различных видов расчёта, и какие расчеты можно проводить, используя условие прочности?

III. Порядок решения типовых задач

 

Задача №1

Двухступенчатый стальной брус нагружен силами F1=30 кН F2=40 кН.

Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение ∆l свободного конца бруса, приняв Е=2∙10 5 МПа. Площади поперечных сечений А1=1,5см2?;А 2 =2см2?

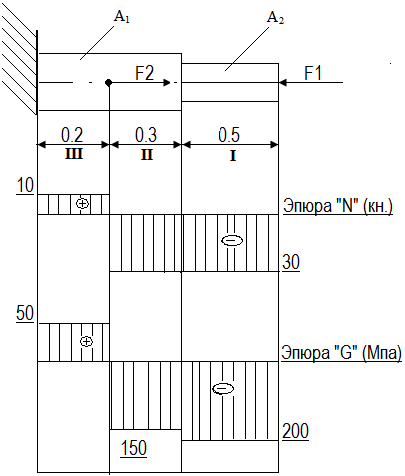
Первая задача требует от студента умения строить эпюры продольных сил, нормальных напряжений и определять удлинения и укорочения бруса.

Последовательность решения задачи

Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и место изменения размеров поперечного сечения.

Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюры продольных сил N. Проведя – параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.

Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянные, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.

Перемещение свободного конча бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.

Решение:

Разбиваем брус на участки.

Определяем ординаты эпюры N на участках бруса:

N1= - F1= -30кН

N2= - F2= -30кН

N3= -F1+F2= -30+40=10 кН

Строим эпюру продольных сил

Вычисляем ординаты эпюры нормальных напряжений

σ1 === –200МПа

σ2 === –150МПа

σ 3=== 50МПа

Строим эпюры нормальных напряжений.

4. Определяем перемещение свободного конца бруса

∆l=∆l1+∆l2+∆l3

∆l1=== – 0,5мм

∆l2=== – 0,225мм

∆l3=== 0,05мм

∆l= - 0,5 – 0,225 + 0,05 = – 0,675мм

Брус укоротился на 0,675мм

Задача № 2

Из условия прочности определить размеры поперечного сечения стержня, удерживающего в равновесии балку, если предел текучести материала σ т=320МПа, заданный коэффициент запаса прочности [n] = 2,5. Расчет провести для двух случаев:

1. поперечное сечение стержня – круг;

2. поперечное сечение стержня – квадрат.

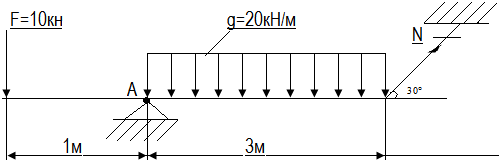
Вторая задача может быть решена студентами, если они будут ясно представлять смысл условия прочности при растяжении (сжатии).

Последовательность решения задачи:

Балку, равновесие которой рассматривается, освободить от связей и заменить действия связей их реакциями;

Составить уравнение равновесия, причем принять за точку, относительно которой определяются моменты, точку в которой установлена опора, и определяем продольную силу N;

Определить из условия прочности площадь поперечного сечения стержня;

Определить для двух случаев размеры поперечного сечения стержня.

Для круга – диаметр d;

Для квадрата – сторону a.

Решение

Составляем уравнение равновесия и определяем продольную силу N

Σ m A=0

N∙sin30°∙3 – 3q∙1,5 + F∙1 = 0

N=== 53,3 кН

2. Определяем допускаемое нормальное напряжение

 

[σ]=	σ	== 128 МПа
	[n]

3. Определяем площадь поперечного сечения стержня

 

σmax	=	N	≤ [σ]→A ≥	N	=	53,3∙103	=416 мм2
		A		[σ]		128

4. Определяем размеры попе речного сечения круга – диаметр d

А=→d===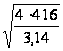 23 мм

5. Определяем размеры поперечного сечения квадрата – сторону a

A=a2→a=== 20,4 мм.

IV. Задания для самостоятельного решения

Задача №1

Проверить прочность стальной тяги ВО диаметром d=20мм,если предел текучести σт =240МПа.требуемый коэффициент запаса прочности [n]=1,5

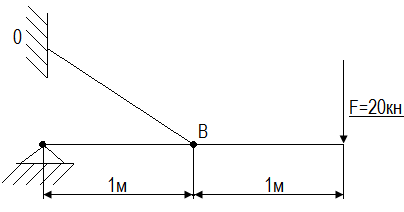
Ответ: перегружена на 58,75%

Задача 2.

Проверить прочность стальных брусьев, если [σ]=160МПа

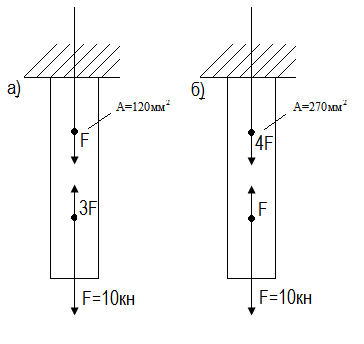
Ответ: а) перегружен на 4,4%

б) недогружен на 7,5%

Задача 3.

Определить требуемую площадь А поперечного сечения стального бруса, если [σ]=160МПа,

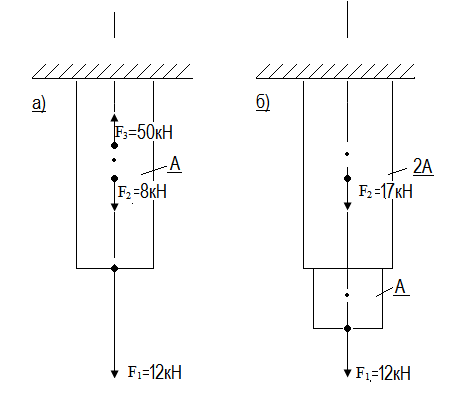
Ответ: а) А=188мм2

б) А=90,6мм2

Задача №4

Определить допускаемую нагрузку для стального стержня, если σт =250МПа, [n]=1,6

Ответ: [F]=31,2кН

Задача №5

Определить размеры поперечного сечения стержня кронштейна, если [σр]=160МПа, [σсж]=120МПа

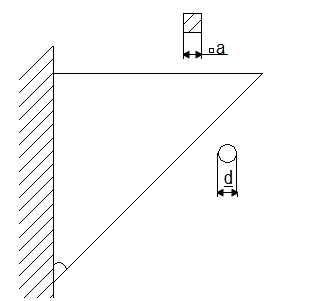
Ответ: а=10мм,d=10мм.