Структура позиційних ігор

Структура позиційних ігор

У багатьох практично важливих конфліктних ситуаціях, маючи в своєму розпорядженні ту або іншу інформацію про їх минулий розвиток, сторони-учасниці виконують свій вибір не раз і назавжди, а послідовно в часі, крок за кроком. Тим самим, вони використовують стратегії, що відображають як динаміку конфлікту, так і ступінь власної інформованості про фактично виникаючій обстановці в розвитку цього конфлікту.

Одним з класів ігор, що описують конфлікти, динаміка яких оказує на поведінку учасників, є так звані позиційні ігри.

Позиційна гра – це без коаліційна гра, що моделює процеси послідовного ухвалення рішень гравцями в умовах змінної в часі і неповній інформації.

Процес гри полягає в послідовному переході від одного стану гри до іншого стану, який здійснюється або шляхом вибору ігроками однієї з можливих дій відповідно до правил гри, або випадковим чином (випадковий хід).

Як приклади позиційних ігор можна привести хрестики-нулики, шашки, шахи, карткові ігри, доміно і ін. Цікаво, що право вибору першого ходу в цих іграх часто визначається випадковим чином.

Стани гри прийнято називати позиціями (звідси і їх назва), а можливі вибори в кожній позиції – альтернативами.

Характерна особливість ПІ – можливість представлення безлічі позицій у вигляді деревовидної впорядкованої множини, яка називається деревом гри (рис. 1).

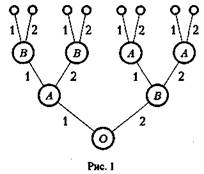
Для визначеності розглядатимемо позиційні ігри, в кожній позиції яких, окрім остаточних, рівно дві альтернативи – перша і друга.

Зауваження. Символ О, А або В в колі вказує, хто з гравців (О, А або В) робить черговий хід в заданій позиції. При цьому символом О зазвичай позначається хід в грі, здійснюваний не гравцем, а яким-небудь випадковим механізмом (іноді його називають природою).

Наприклад, в ПІ, представленою на рис. 1 своїм деревом, перший хід проводиться випадково.

Користуючись графічним описом гри, можна сказати, що процес гри полягає в переході від початкової позиції до остаточної через безпосередньо наступні  одна за іншою проміжні позиції.

Кожна остаточна вершина визначає єдиний ланцюг (послідовність ланок, що йдуть один за одним), що зв'язує початкову вершину з даною (рис. 2). Такий ланцюг називається партією. На рис. 2 одна з партій виділена жирними лініями. Число різних партій рівне числу вирішальних вершин (позицій).

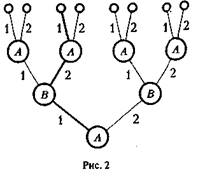
У кожній остаточній позиції заданий числовий виграш гравця А.

Зауваження. Ми розглядатимемо тут тільки антагоністичні ПІ.

У шахах функція виграшів гравця А (білих) визначається так:

+1 на партіях, що виграються

  0 на нічийних партіях

-1 на партіях, що програються.

Функція виграшів гравця В (чорних) відрізняється від функції виграшів білих тільки знайомий.

Розрізняють ПІ з повною інформацією і ПІ з неповною інформацією.

Позиційна гра називається грою з повною інформацією, якщо в кожній позиції будь-якої її партії гравець, що робить хід, знає, які альтернативи були вибрані на попередніх ходах. У графічному описі кожна вершина дерева такої гри є окрему інформаційну більшість.

Прикладами позиційних ігор з повною інформацією можуть служити кре-стики-нулики, шашки і шахи.

В каждой окончательной позиции задан числовой выигрыш игрока А.

Прикладами позиційних ігор з повною інформацією можуть служити кре-стики-нулики, шашки і шахи.

Основна особливість позиційної гри з повною інформацією полягає в тому, що відповідна нею матриця виграшів завжди має сідлову точку, тобто в грі з повною інформацією існують оптимальні чисті стратегії і, значить, рівноважна ситуація.

Сказане означає, що в шахах (хрестиках-нулях, шашках) вже в початковій позиції або є спосіб виграшу за білих, або спосіб вийгришу за чорних, або як та, так і інша сторона здатна форсувати нічью.

У ПІ з неповною інформацією (приклад – доміно) гравець, що робить хід, не знає точно, в якій саме позиції дерева гри він фактично знаходиться. Цьому гравцеві відома лише деяка безліч позицій, включаючи в себе його фактичну позицію. Така більшість називаеться інформаційною множиною.

Таким чином, в ПІ з неповною інформацією гравець при своєму ході знає, в якій інформаційній множині він знаходиться, але йому невідомо, в якій саме позиції цієї множини.