Ітераційний метод рішення матричних ігор

Ітераційний метод рішення матричних ігор

Опишемо метод відшукання рішення матричної гри - ціни гри й оптимальних змішаних стратегій, певною мірою вірно відображає деяку реальну ситуацію нагромадження досвіду поступового вироблення гравцями гарних стратегій у результаті багатьох повторень конфліктних ситуацій. Основна ідея цього методу укладається в тім, щоб подумки як би змоделювати реальне практичне «навчання» гравців у ході самої гри, коли кожний із гравців на власному досвіді прощупує спосіб поводження супротивника й намагається відповідати на нього найбільш вигідним для себе чином. Іншими словами, щораз при поновленні гри гравець вибирає найбільш вигідну для себе стратегію, опираючись на попередній вибір супротивника.

Проілюструємо цей метод на прикладі гри, заданою матрицею

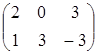
(тут maxmin = 0, minmax = 2 , тобто сідловок точки немає).

Опишемо правила вибору ходів гравцями, припустивши, для визначеності, що починає гравець А:

хід гравця А – стратегія А₁ – (2   0   3);

гравець В  вибирає свою стратегію так, щоб виграш гравця А був мінімальний:

хід гравця В – стратегія В₂ –

гравець А вибирає свою стратегію так, щоб його виграш при стратегії В₂ гравця В був максимальний:

хід гравця А – стратегія А₂ – (1    3    –3);

гравець В вибирає свою стратегію так, щоб «накопичений» виграш гравця А при стратегіях А₁ й  А₂

(2   0   3) + (1  3   -3) = (3   3   0),

був мінімальний:

хід гравця В – стратегія В₃ –

гравець А вибирає свою стратегію так, щоб його «накопичений» виграш при стратегіях В₂ й B₃ гравця В

+ = ,

був максимальний:

хід гравця А – стратегія А₁ – (2   0   3);

гравець В вибирає свою стратегію так, щоб «накопичений» виграш гравця А при стратегіях А₁, А₂  й А₁

(3   3   0) + (2   0   3) = (5   3    3),

був мінімальний:

хід гравця В – стратегія В₂ –

і т.д.

Розіб'ємо послідовні ходи гравців А и В на пари (хід гравця А, хід гравця В) і запишемо результати в таблицю, що вимагає деяких пояснень.

Опис таблиці

1-й стовпець – номер n кроку (пари послідовних ходів гравців А и В),

2-й стовпець – номер i стратегії, обраної гравцем А,

3-й стовпець – «накопичений» сумарний виграш гравця А

    за перші n кроків при стратегії В₁ гравця В,

4-й стовпець – «накопичений» сумарний виграш гравця А           

    за перші n кроків при стратегії В₂  гравця В,

5-й стовпець – «накопичений» сумарний виграш гравця А

     за перші n кроків при стратегії В₃ гравця В,

6-й стовпець – мінімальний середній виграш гравця А, рівний мінімальному накопиченому їм виграшу за перші n кроків, діленому на число цих кроків,

7-й стовпець – номер k стратегії, обраної гравцем В,

8-й стовпець – «накопичений» сумарний виграш гравця А

    за перші n кроків при стратегії А₁,

9-й стовпець – «накопичений» сумарний виграш гравця А

  за перші n кроків при стратегії А₂,

10-й стовпець – максимальний середній виграш гравця А, рівний максимальному накопиченому їм виграшу за перші n кроків, діленому на число цих кроків,

11-й стовпець – середнє арифметичне мінімального середнього виграшу й максимального середнього виграшу гравця А.

Рішення гри визначається приблизно по закінченні кожного із кроків.

Наприклад, за наближену ціну гри можна взяти середнє арифметичне , отримане на n-м кроці. Змішані стратегії супротивників визначаються частотами появи чистих стратегій.

Після 9-го кроку маємо

 = 1,00.

При цьому гравець А 6 разів використав стратегію А₁ й 3 рази стратегію А₂ .У свою чергу гравець В 6 разів застосовував стратегію В₂, 3 рази стратегію В₃ , а стратегією В₃1 не користувався взагалі. Звідси одержуємо, що

після 10-го кроку одержуємо -

Дана гра легко вирішується графічно. От точна відповідь:

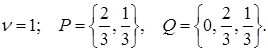
Порівнюючи результати, отримані на 9-м, 10-м, а також 11-м й 12-м кроках:

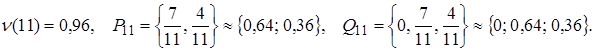
зауважуємо, що в міру збільшення числа кроків значення усе менше відрізняються від точних.

Зауваження 1. При збільшенні числа кроків всі три величини  будуть наближатися до ціни гри v, але середнє арифметичне v(n) буде наближатися до v порівняно швидше.

Зауваження 2. Хоча збіжність ітерацій досить повільна, проте, навіть такий невеликий розрахунок завжди дає можливість знаходити орієнтоване значення ціни гри й частки чистих стратегій.

Зауваження 3. Порівняно повільна швидкість збіжності можна пояснити цілим рядом причин. Укажемо одну з них, психологічно найцікавішу. Якщо, приміром, гравець А вже одержав оптимальну змішану стратегію, то він не схильний зупинятися на ній. Аж ніяк немає – він продовжить спроби виграти в супротивника В побільше, особливо якщо останній ще не досяг оптимальної змішаної стратегії. Тим самим, гравець А може мимоволі погіршити своє положення.

Зауваження 4. Відзначимо дві основних переваги описаного методу:

1) ітераційний метод простий й одночасно універсальний (при його допомозі можна легко знайти наближене рішення будь-якої матричної гри),

2) обсяг і складність обчислень порівняно слабко ростуть у міру збільшення числа стратегій гравців (розмірів матриці гри).