Узагальнення методів рішення ігор

Узагальнення методів рішення ігор

Матричні ігри моделюють конфліктні ситуації, у яких кожна зі сторін-учасниць робить свій хід одночасно із другою стороною.

При цьому найбільший інтерес представляє випадок, коли гра не закінчується відразу ж після здійснення гравцями однієї такої пари одночасних ходів, а повторюється багаторазово. Причому вважається, що перед кожним поновленням гри гравці не одержують ніяких нових відомостей ні про конфлікт, ні про можливі дії противної сторони. тобто при багаторазовому повторенні матричної гри кожна зі сторін щораз виявляється перед вибором деякої стратегії з того самого безлічі стратегій, незмінного в кожного із гравців.

Проте, у таких багаторазово повторюваних обставинах більшу роль грає аналіз гри, як попередній, так і проміжний.

У результаті розумно проведеного попереднього аналізу матричної гри зацікавлена в аналізі сторона може визначити свою лінію поводження (правило вибору стратегій) на всю серію ігор.

Розглянутий вище максиміний підхід є далеко не єдиними коштами. Однак не слід забувати, що принциповою особливістю цього підходу є та обставина, що гравець, що дотримується виведеного на його основі правила вибору стратегій, заздалегідь може досить точно оцінити нетривіальні розміри свого гарантованого виграшу. Крім того, максиміний підхід дозволяє зводити завдання пошуку рішення гри до розгляду порівняно нескладних завдань лінійного програмування й, тим самим, одержувати ефективні рекомендації з тому, як краще вибирати стратегії в конкретній грі при багаторазовому її повторенні.

Якщо гра повторюється багато разів, то деякі додаткові відомості - які саме стратегії вибирає противна сторона і які правила вибору стратегій вона керується - гравець все-таки одержує. На підставі цих відомостей і результатів попереднього аналізу гри він може досить точно оцінити супротивника й, якщо той не дотримується компромісного максиміного підходу, внести відповідні зміни у власну лінію поводження й збільшити виграш.

Основні етапи пошуку рішення матричних ігор

1-й етап – перевірка наявності (або відсутності) рівноваги в чистих стратегіях (при наявності рівноважної ситуації вказуються відповідні оптимальні стратегії гравців і ціна гри).

2-й етап – пошук домінуючих стратегій (у випадку успіху цього пошуку — відкидання домінуючих рядків і стовпців у вихідній матриці гри).

3-й етап – заміна гри на її змішане розширення й відшукання оптимальних змішаних стратегій і ціни гри.

Розглядаючи біматричні ігри, розумно спробувати відразу ж перейти до змішаних стратегій гравців (цим ми припускаємо, що кожна гра може бути багаторазово повторена в незмінних обставинах).

При змішаних стратегіях у біматричних іграх виникають середні виграші гравців А и В, обумовлені за правилами, у яких уже немає ніякої дискримінації гравця В:

,     .

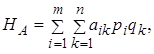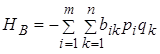В 2 ( 2 біматричній грі платіжні матриці гравців мають такий вигляд

,     ,

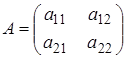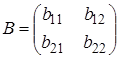імовірності

а середні виграші обчислюються по формулах

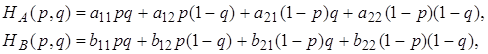
де

,

1)                    Одним із класів ігор, що описують конфлікти, динаміка яких впливає на поводження учасників, є так називані позиційні ігри.

Позиційна гра – це безкоаліційна гра, що моделює процеси послідовного прийняття рішень гравцями в умовах мінливої в часі й неповній інформації.

Процес гри складається в послідовному переході від одного стану гри до іншого стану, що здійснюється або шляхом вибору гравцями однієї з можливих дій відповідно до правил гри, або випадковим чином (випадковий хід).

Заздалегідь певну послідовність ходів гравця, обрану їм залежно від інформації про ходи іншого гравця й ходах гравця О (природу), будемо називати чистою стратегією цього гравця.

В тім випадку, якщо в грі немає випадкових ходів (гравець О в грі не бере участь), вибір гравцем А и гравцем В чистих стратегій однозначно визначає результат гри – приводить до остаточної позиції, де гравець А и одержує свій виграш. Ця обставина дозволяє зводити ПІ до матричної гри.

Процес відомості ПІ до матричного називається нормалізацією позиційної гри.