Задачи с элементами конструирования

Задачи с элементами конструирования

В программе курса черчения обращается особое внимание на развитие творческих способностей учащихся в процессе их графической подготовки, на необходимость формирования у них приемов решения несложных конструкторских задач.

Для реализации требований программы необходимо обучить школьников приемам творческой деятельности, необходимым для овладения умениями, связанными с конструированием.

На начальных этапах приобщения школьников к решению творческих задач следует, по нашему мнению, ограничиться конструированием элементов деталей или реконструкцией их частей. Заниматься конструированием технических объектов в целом, как думают некоторые, не следует, так как такие занятия выходят за рамки обучения черчению и возможны лишь в процессе кружковых занятий техническим творчеством.

Для оказания помощи учащимся при выполнении заданий было решено вводить в них наглядную опору путем использования сопрягаемых деталей. Исключением является задание, приведенное в учебнике на рисунке 159, в котором предлагается осуществить конструирование дета ли по образцу с соблюдением правил нанесения размеров повторяющихся элементов изделия.

В связи с рассмотрением содержания заданий в учебнике обратим внимание на особенность задачи, приведен- ной на рисунке 260 учебника (в изданиях до 2007 г.). Эта задача отличается тем, что в ней предлагается разработать конструкцию деталей по принципиальной схеме изделия, что достаточно трудно.

С целью оказания помощи учащимся целесообразно поручить создание конструкции деталей «захват» и «траверса» двум рядом сидящим учащимся, с тем чтобы они мог- ли согласовать разработку взаимного сопряжения их фор- мы и размеров.

Но этой помощи может оказаться недостаточно. В этом случае полезно воспользоваться советами психологов о целесообразности введения «наводящих» задач, состоящих в том, что надо находить такие предваряющие или сопутствующие задачи, вопросы или упражнения, которые, не являясь прямой подсказкой, подводят учащихся к решению. Применительно к данной задаче наведением может служить обращение к изображениям съемников, приведенных на рисунке 249 учебника. Здесь учащиеся увидят, что «захваты» могут по-разному соединяться с «коромыслом», а само «коромысло» (а в нашем задании «траверса») может быть с прорезями или без них. Такое «наведение» обогатит представления учащихся о возможных конструкциях сходных деталей.

Решение большинства из приведенных в учебнике заданий связано с изменением формы деталей или их заготовок путем образования в них вырезов, срезов или отверстий. Заметим, что эти действия осуществляются и при решении задач на преобразование по изображениям.

Многие учителя отождествляют задачи на преобразование с задачами на конструирование, при этом не учитывая, что они cвязаны с разными способами деятельности и направлены на развитие разных качеств мышления и умений у учащихся.

Покажем эти особенности на примере. В учебнике на рисунке 259, а дана задача с элементами конструирования, в которой предлагается из данной заготовки сконструировать опору для установки в вертикальном положе- нии в ее верхней части цилиндрического стержня, пред- усмотрев возможность крепления основания опоры на столе при помощи болтов. При этом сказано, что желательно также, насколько это возможно, уменьшить массу опоры. При решении этой задачи учащийся должен самостоятельно решить три вопроса. Во-первых, как установить в верхней части детали стержень, диаметр которого больше размера выступа в опоре. Тут могут быть два решения: можно образовать отверстие в опоре, равное по размерам диаметру стержня, и вставить его в опору (рис. 27, а). Другое решение состоит в том, чтобы сделать вырез в стержне (рис. 27, б) и насадить его на выступ в верхней части опоры. Оба эти решения правомерны, но, забегая вперед, скажем, что с технической и методической точки зрения они неправомерны. С технической стороны при втором решении стержень будет установлен менее надежно, даже если закрепить его при помощи штифта. С методической стороны более полезно первое решение, так как чертеж верхней части опоры в проекционном отношении получается более ценным.

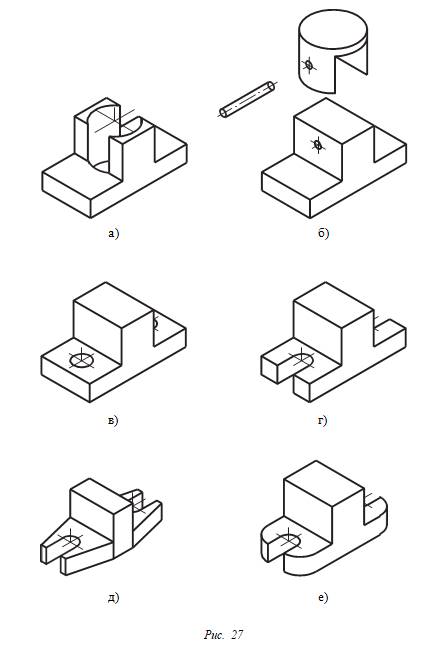
Во-вторых, предстоит решить, какое конструктивное решение следует принять с целью обеспечения возможности крепить опору на столе. Тут также возможны два решения: образовать два отверстия в ее основании (рис. 27, в) или предусмотреть две прорези (рис. 27, г, д).

В-третьих, надо, насколько это возможно, облегчить массу опоры. Тут необходимо иметь в виду, что если образовать отверстие в ее средней части и два отверстия в основании, то масса опоры значительно уменьшится. Но возникает вопрос, как еще уменьшить массу.

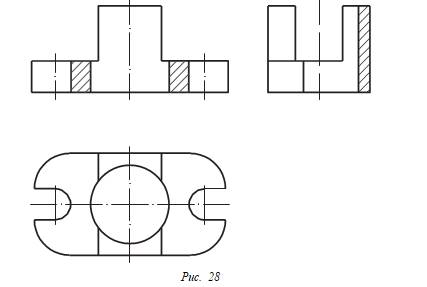
Учащийся должен догадаться, что если есть еще другие возможности — скруглить или срезать углы в основании (рис. 27, е). При этом целесообразно предпочесть конструкцию с вырезами в основании, а не с отверстиями в нем. Завершенная конструкция опоры показана на рисунке 28.

Мы привели подробный анализ решения задания с элементами конструирования и показали, какие богатые возможности они содержат для развития учащихся в содержательном, творческом и графическом отношениях.

Теперь обратимся к тому, как изменилась бы постановка задачи и ее содержание, если иметь в виду использова-

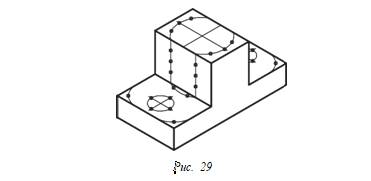
      ние ее для обучения преобразованию изображений. В этом случае условие задачи (рис. 29) будет  сформулировано  так: мысленно просверлите сквозное отверстие 30 в детали и обработайте ее нижнюю часть по нанесенной разметке.

Нетрудно заметить, что в этом случае конечная форма детали будет такой же, как и описанная выше. Но деятельность учащихся при этом будет принципиально различной. При решении задачи на преобразование по изображениям все действия учащихся строго регламентированы, что должно привести в конечном итоге к единственному решению. Указано, какие отверстия и срезы, какого диаметра и радиуса должны быть и в каких местах их надо выполнить. Деятельность учащихся при этом носит исполнительский характер, никакого творческого начала в ней нет.

Совсем другую направленность имеет деятельность учащихся при решении задачи с элементами конструирования. В этом случае им предлагается добиться конечного результата (установить сопрягаемую деталь и уменьшить массу), а как это сделать, учащийся должен решить самостоятельно. Его действия при этом не регламентируются, а только направляются.

Возникает вопрос: полезно ли решение задач на преобразования для формирования приемов конструирования? Ответ состоит в том, что те и другие задачи включают тесно взаимосвязанные, но разные виды деятельности. Взаимосвязь заключается в том, что задачи на преобразования содействуют развитию динамических пространственных представлений учащихся и приобщают их к таким действиям, как изменение формы предметов путем удаления, наращивания, замены частей или изменения их глубинных соотношений, комбинирование частей предметов и т.п. Такая направленность содержания задач позволяет приблизить учащихся к овладению действиями, характерными для рационализации, реконструкции и конструирования.

Что касается вопроса о развитии подвижности пространственных представлений учащихся при решении задач, связанных с преобразованиями по изображениям, то развитие образного мышления учащихся в этом направлении имеет значение и для конструкторской деятельности. Эту сторону развития интеллектуальных способностей учащихся следует рассмотреть более подробно.

Многие полагают, что представление о новой конструкции во всех ее деталях создается вначале мысленно, как говорят, в «голове конструктора» и чертеж является только средством выражения замыслов инженера. Такое понимание приводит к убеждению, что главным качеством мышления, обеспечивающим успешную конструкторскую деятельность, является развитое пространственное представление человека, умение мысленно создать, удержать и адекватно воспроизвести новый или видоизмененный об- раз изделия на чертеже.

В действительности конструктор в начале работы сохраняет в своем сознании только основные элементы конструкций. Далее в процессе выполнения чертежей эти элементы выясняются и уточняются. В результате зачастую бывает так, что основная идея конструкции претерпевает    в  процессе  конструирования   существенные   изменения. В процессе этой работы пространственное воображение и выполняемый чертеж взаимно дополняют и обогащают друг друга, они взаимно и неразрывно связаны.

Психологи также заметили широкое распространение мнения, что условием успешной конструкторской деятельности является пространственное воображение. По- этому, как отмечается, многие полагают, что усилия должны быть направлены на формирование именно этой стороны образного мышления. Однако умение оперировать зрительными образами является важной, но не глав- ной особенностью конструкторской деятельности. Особая значимость при этом придается логическому мышлению и

деятельности, связанной с различными преобразованиями исходных данных, в том числе по аналогии и комбинаторного характера. Установлено также, что на определенных этапах работы конструктора участие пространственного воображения вообще нежелательно, так как способность создавать устойчивые образы мешает дальнейшему поиску.

Из сказанного следует, что благоприятные условия для введения элементов конструирования в процесс обучения создаются при определенной направленности специальных видов заданий, развивающих способность к различным изменениям и комбинированию исходных графических данных в условиях творческого поиска решений.

Для развития творческих способностей учащихся и специальных умений, связанных с элементами конструирования, необходима систематическая, достаточно дли- тельная и целенаправленная работа по формированию у школьников принципиально новых приемов учебной работы. В связи с этим в организационном отношении сразу возникает вопрос: где взять время для такого обучения? Учитывая жесткие рамки, отведенные учебным планом на изучение курса черчения, возможными являются два пути: введение кратковременных заданий с элементами конструирования в начале или конце урока и специальное обучение в часы, отведенные на факультативные занятия и кружковую работу.

В учебную практику должны быть введены новые виды специальных задач, органически сочетающихся с творческим поиском при обучении элементам конструирования. Попытаемся в первом приближении сформулировать требования, которыми следует руководствоваться при созда- нии новых задач с элементами конструирования:

• главное в задачах — их направленность на сообразительность, самостоятельный творческий поиск решения, комбинирование исходных данных или учет формы и размеров сопрягаемых деталей;

• набор задач должен быть разнообразным. Важно, чтобы одни из них позволяли найти решение только путем перекомпоновки частей деталей, а другие требовали пре- образования или принципиального изменения их конструкции, допуская при этом возможность и простого, и сложного решения;

• предпочтительно, чтобы задачи можно было решать в нескольких вариантах, выбор одного из которых учащийся мог бы аргументировано обосновать;

• желательно, чтобы в условии содержалась в скрытом виде подсказка, облегчающая поиск решения, или, наоборот, какой-либо элемент, отвлекающий от нахождения действительно рационального, но простого ответа;

• целесообразна максимальная простота графического оформления конечного результата;

• задачи не должны содержать неизвестных для учащихся технико-технологических сведений;

• важным условием педагогической эффективности содержания задач является возможно более полное соблюдение межпредметных связей, особенно с математикой и трудовым обучением.

Приведем примеры задач, отвечающих этим требованиям.

Пример 1. На основе чертежа, приведенного на рисунке 30, предлагается осуществить конструктивные изменения опоры путем введения новых элементов (отверстий или вырезов), чтобы значительно облегчить ее массу, не нарушая общей формы и пропорций частей детали. Задача эта несложная, но решение ее требует проявления самостоятельного поиска в выборе формы и положения отверстий или вырезов в детали (об этом есть подсказка в условии задачи).

Пример 2. На рисунке 31 дан чертеж детали резко выраженной асимметричной формы. Конструкторская за-

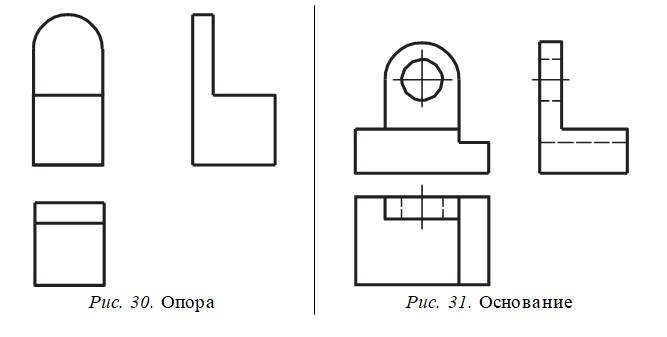
дача состоит в том, чтобы мысленно изменить число частей детали или ее элементов, с тем чтобы придать ей симметричную форму. Задача требует сообразительности и развивает умение комбинировать исходные данные, так  как возможно несколько решений. Особенность этой задачи состоит в том, что в ходе ее решения сочетается выполнение технического задания с необходимостью изменения графического состава изображения (взаимная замена штриховых и сплошных толстых основных линий чертежа). При этом правильное выполнение данного задания связано с отчетливым представлением значения понятия

«симметрия». В связи с этим надо иметь в виду, что на уроках математики школьники получают представление только о симметрии относительно точки и линии, а понятие о симметрии относительно плоскости применительно   к пространственным формам складывается на основе их житейских представлений, что требует от учителя необходимых разъяснений.

Пример 4. В этой задаче (рис. 33, а) требуется мысленно изменить сочетание частей вилки так, чтобы новая конструкция детали имела размер: длину 40 мм и высоту 50 мм. При этом вновь созданная деталь должна устойчиво стоять на горизонтальной плоскости.

Эта задача на перекомпоновку частей детали. Особенность задачи состоит в том, что ее нельзя решить обычны- ми приемами, опираясь на образное мышление. Решение следует начинать с расчета. Для этого надо сообразить, что для изменения длины детали с 52 до 40 мм необходимо уменьшить ее на 12 мм. Только после этого можно оп-

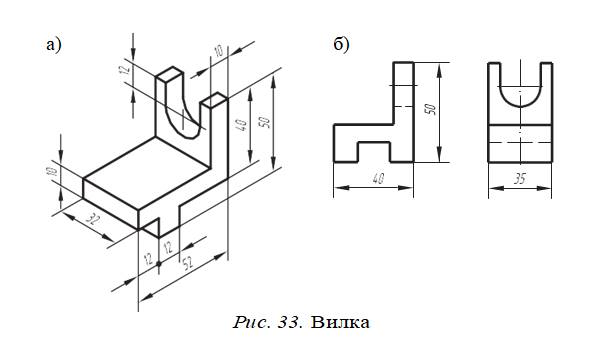
ределить, какую часть детали нужно отделить и куда ее переставить, чтобы вилке придать форму, отвечающую условию задачи (обеспечение ее устойчивого положения на горизонтальной плоскости). Решение показано на рисунке 33, б.

• введение нового элемента (отверстия, выреза и др.) в деталь;

• изменение числа частей и элементов деталей;

• изменение формы деталей путем удаления, наращивания или дополнения их частей и элементов;

• перекомпоновка или комбинирование частей или элементов деталей;

• новое сочетание геометрических размеров частей или элементов деталей.

Особенность деятельности учащихся при освоении приемов конструирования, как уже указывалось выше, состоит в том, что выбор того или иного действия должен осуществляться учащимися самостоятельно, исходя из конечной цели, поставленной в условии задачи.

Цели могут быть разнообразными и зависеть от формы объектов, их назначения и требований, предъявляемых к предметам в условиях эксплуатации.

Так, цели могут заключаться в необходимости измене- ния: формы предметов (чтобы добиться симметричности, устойчивости на плоскости, уравновешенности); массы де- тали (с целью ее уменьшения или перемещения центра приложения); габаритных  размеров  или  размеров  частей и элементов деталей (с целью обеспечения возможности присоединения данной детали к сопрягаемой с ней) и др. Постановка таких целей является новым и непривычным делом для учащихся, что требует соответствующей разъяснительной работы учителя, так как надо формировать перестройку мышления школьников.

Мы рассмотрели следующие виды конструкторских задач:

• доконструирование деталей с учетом формы сопрягаемой детали;

• перенесение принципа действия с одной конструкции на другую;

• восполнение недостающего звена в конструкции;

• проектирование схематически заданной конструкции;

• конструирование изделий по заданным техническим требованиям.

Можно полагать, что такой набор видов задач является вполне достаточным для первоначального этапа обучения школьников элементам конструирования.

В заключение надо сказать, что усилия учителей и методистов должны быть направлены не только на поиск новых методических подходов, готовящих учащихся к решению задач с элементами конструирования, но и на раз- работку новых вариантов таких задач.

Примечание. Задачи на анализ геометрической формы предметов, построение чертежей деталей с применением геометрических построений, чтение чертежей, выполнение эскизов и др. даны в разделе «Чтение и выполнение чертежей деталей». Задачи и упражнения при изучении разрезов и сечений содержатся на страницах 214–221, сборочных чертежей — в разделе «Сборочные чертежи».