
Название работы:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ И МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ОБУЧАЮЩИХСЯ ОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
Автор работы:
Шкурина Надежда Анатольевна, преподаватель
Образовательная организация:
КГБПОУ «Техникум горных разработок имени В.П. Астафьева», п. Ирша
Министерство образования Красноярского края
Краевое государственное бюджетное профессиональное образовательное учреждение
«Техникум горных разработок имени В.П. Астафьева»
Учебно-методическое пособие для обучающихся
по дисциплине «Математика»
Задания для самостоятельной работы и методические рекомендации для обучающихся очной формы обучения по профессии:
19.01.17 Сварщик (электросварочные и газосварочные работы)
35.01.13 Тракторист – машинист сельскохозяйственного производства
21.01.08 Машинист на открытых горных работах
19.01.17 Повар, кондитер
1-е издание
Составитель:
Шкурина Надежда Анатольевна,
преподаватель математики
Введение
Данное учебное пособие представляет собой составную часть комплекта методических рекомендаций, разработанных преподавателем математики H. А. Шкуриной для обучающихся очной формы обучения и имеет своей целью помочь обучающимся в изучении дисциплины «Математика», в приобретении необходимых навыков решения задач и выполнении самостоятельных работ по указанному разделу курса.
Устойчивые математические навыки у обучающихся вырабатываются успешнее, если ввести в учебный процесс специальные предписания и планы решения важнейших задач. Именно они служат пропедевтикой формирования в дальнейшем у обучаемых алгоритмической культуры. С другой стороны, твердое знание планов решения основных задач курса алгебры и начал анализа — это первоначальный фундамент математической подготовки обучающихся.
Применяя планы решения задач в процессе обучения математике, надо ориентировать обучающихся на то, что им следует не просто запомнить тот или иной план, но главное понять, на каких теоретических предложениях основано его применение, и каждый шаг учебной деятельности, осуществляя по заданным предписаниям, выполнять сознательно, а не автоматически.
При составлении каждого такого плана я руководствовалась следующими принципами:
1. Теоретический фундамент плана должны составлять теоретические сведения, имеющие непосредственное к нему отношение.
2. Система предписаний, имея дискретный характер, должна быть общей по отношению к целому классу однородных задач.
3. По содержанию система предписаний должна быть полной или достаточной, т.е. обеспечивать на каждом конкретном шаге учебной деятельности обучающихся однозначное получение промежуточной информации, которая в своем комплексе гарантирует получение конечного результата.
4. Система предписаний должна быть совместной или непротиворечивой, т. е. каждое предыдущее предписание (или группа предписаний) должно являться малой посылкой (подводящей) для последующего, а последующее — логическим следствием предыдущих.
5. Число пунктов плана не должно быть большим (предельная норма 5—6). Это обеспечивает его подвижность: объединение отдельных шагов или дробление шагов на более элементарные.
6. Система предписаний должна обеспечивать многократное решение однотипных задач, т. е. обладать свойством массовости.
Знакомство обучающихся с планами решения задач осуществляется на уроках изучения нового материала, дальнейшая их отработка выполняется на практических занятиях при различных формах работы (фронтальной, групповой, индивидуальной).
Мною разработана система специальных карточек – инструкций (раздаточный дидактический материал). Каждая карточка - инструкция отражает определенный вопрос программы и предусматривает отработку соответствующего ее названию плана, который скоординирован в таблицу.
Структура карточек - инструкций одна и та же. Каждая из них включает план, основные сведения из теории, иллюстрацию применения плана к решению задач, задания для самостоятельной работы. Наряду с формулировкой любого шага плана показано его практическое применение. Это обеспечивает работу обучающихся по образцу на каждом этапе выработки учебного навыка.
Программой и учебным планом указанных специальностей на первом курсе предусмотрено выполнение самостоятельных работ по следующему разделу курса математики: «Производная и ее применение».
Пособие содержит:
- примеры решения типовых задач, снабженные необходимый теоретическим материалом и подробными пояснениями;
- приложения, включающие сводку формул элементарной математики, таблицу производных, схемы-алгоритмы решения типовых задач математического анализа.
1. Общие рекомендации
Основной формой обучения обучающегося является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по учебникам, решение задач, самопроверка, выполнение контрольных работ. Преподаватель организует чтение лекций и проведение практических занятий, цель которых обратить внимание на общую схему построения соответствующего раздела курса, подчеркнуть важнейшие места, указать главные практические приложения теоретического материала, привести факты из истории науки. Кроме того, на этих занятиях могут быть более подробно рассмотрены отдельные вопросы программы, отсутствующие, или недостаточно полно освещенные в рекомендуемых учебных пособиях.
Завершающим этапом изучения отдельных частей курса математики является контрольная работа в соответствии с учебным планом.
Изучив материал, следует переходить к следующему вопросу только после усвоения предыдущего, производя на бумаге все вычисления (в том числе и те, которые для краткости опущены в учебнике) и выполняя необходимые чертежи.
Особое внимание следует обращать на определение основных понятий. Обучающийся должен подробно разбирать примеры, которые поясняют такие определения, и уметь строить аналогичные примеры самостоятельно.
При изучении материала полезно вести конспект, в который рекомендуется выписывать определения, формулировки теорем, формулы, уравнения и т.д. На полях конспекта следует формулировать вопросы, которые обучающийся считает необходимым задать преподавателю на консультации.
При изучении математики рекомендую пользоваться следующей литературой:
1. Учебник: Алгебра и начала анализа для 10 – 11классов средней школы под редакцией А.Н. Колмогорова.
2. Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы.
3. Башмаков М.И. Математика: учебник для студ. учреждений сред. проф. образования. — М., 2014.
При решении задач нужно обосновывать каждый этап решения исходя из теоретических положений курса.
Решения задач и примеров следует излагать подробно, вычисления располагать в строгом порядке, отделяя вспомогательные вычисления от основных. Чертежи можно выполнять от руки, но аккуратно и в соответствии с данными условиями. Если чертеж требует особо тщательного выполнения (например, при графической проверке решения, полученного путем вычислений), то следует пользоваться линейкой, транспортиром, лекалом и указывать масштаб. Необходимо также выписывать формулы, используемые в процессе решения задачи.
Решение каждой
задачи должно доводиться до ответа, требуемого условием. В промежуточных вычислениях
не следует вводить приближенные значения корней, числа ![]() и
т.п.
и
т.п.
Полученный ответ следует проверять способами, вытекающими из существа данной задачи. Если, например, решалась задача с конкретным физическим или геометрическим содержанием, то полезно прежде всего проверить размерность полученного ответа. Полезно также, если возможно, решить задачу несколькими способами и сравнить полученные результаты.
Решение задач определенного типа нужно продолжать до приобретения твердых навыков в их решении.
После изучения определенной темы и решения достаточного количества соответствующих задач обучающемуся рекомендуется воспроизвести по памяти определения, выводы формул, формулировки и доказательства теорем. В случае необходимости надо еще раз внимательно прочитать учебники решить ряд задач.
Иногда недостаточность усвоения того или иного вопроса выясняется только при изучении дальнейшего материала. В этом случае следует вернуться назад и повторить плохо усвоенный раздел.
Важным критерием усвоения теории является умение решать задачи на пройденный материал. Однако умение решать простые задачи не означает глубокого понимания теории. Поэтому обучающиеся должны уделять достаточное внимание изучению теоретического материала.
Если в процессе изучения теоретического материала или при решении задач у обучающегося возникают вопросы, разрешить которые самостоятельно не удается (неясность терминов, формулировок теорем, отдельных задач и т.д.), то он может обратиться к преподавателю для получения от него письменной или устной консультации.
В своих вопросах обучающийся должен точно указать, в чем он испытывает затруднение. Если обучающийся испытывает затруднение при решении задачи, то следует указать характер этого затруднения, привести предполагаемый план решения.
2. Раздел курса математики: «Производная и ее применение»
Приращение функции. Производная функции. Правила дифференцирования. Уравнение касательной. Признак возрастания (убывания) функции. Экстремумы. Наибольшее и наименьшее значения функции. Схема исследования функции. Исследование функции.
|
|
1. Приращение аргумента и приращение функции На рисунке
Задание. Вычислить приращение функции f (x) в произвольной точке, если: а) f (x) = 2x2 + 3x– 5; б) f(x) = sin2x. |
|
№ шага |
План вычисления приращения функции |
Применение плана |
|
|
f(x) = 2x2 + 3x0 - 5 |
f(x) = sin2x |
||
|
1 |
Фиксируем произвольное значение аргумента х0 и находим значение функции f(x0) |
x = x0, f (x0) = 2x02 + 3x0 - 5 |
x= x0, f (x0) = sin2x0 |
|
2 |
Задаем аргументу приращение находим значение функции f(x0 + |
x= x0 + f (x0+ =2x02 + 4x0 |
x= x0 + f (x0+ |
|
3 |
Находим приращение функции: ∆f = f (x0 + |
|
|
Примеры. Вычислите приращение функции f(x) в произвольной точке х, если
Примеры. Вычислите приращение функции f(x) в произвольной точке х, если: f(x) = 3x – 8; 2) f(x) = 2 – x2; 3) f(x) = x3 + 4;
4) f(x) = ![]() ; 5) f(x) =
; 5) f(x) = ![]() ; 6) f(x) = 7x; 7) f(x) = sin
; 6) f(x) = 7x; 7) f(x) = sin![]() ; 8) f(x) = 1 – cos x; 9) f (x) = tg3x
; 8) f(x) = 1 – cos x; 9) f (x) = tg3x
Карточка-инструкция по теме «Производная функции»
2. Производная функции
Определение. Производной функции y
= f(x) в заданной точке x называется предел отношения приращения функции ∆y в этой точке к приращению аргумента ∆x, когда ∆x стремится к нулю,
т.е. f ' (x) =![]() =
=![]() .
.
Задание. Вычислите производную функции f(x) в точке x0
= 2, если: а) f(x) = 3x2 - 5x+1; б) f(x) =![]()
|
№ шага |
План вычисления производной функции |
Применение плана |
|
|
а) f(x) = 3x2 - 5x+1 |
б) f(x) = |
||
|
1 |
Фиксируем точку x и даем аргументу
приращение |
x, x+ |
x, x+ |
|
2 |
Вычисляем приращение функции:
|
∆f=(3(x+∆x)2 - 5(x+∆x) +1)-(3x2-5x+1)= = 6x∆x+3(∆x)2-5∆x |
∆f = = |
|
3 |
Находим отношение приращения функции к приращению
аргумента: |
|
|
|
4 |
Вычисляем производную: f '(x)= |
f '(x)= |
f '(x) = = |
|
5 |
Вычисляем f '(x0) |
f '(2) = 6 |
f '(2)= |
Примеры. Вычислите производные следующих функций: 1) f(x)=2x+3 в точке x=3; 2) f(x)= 3x2 - 2 в точке x=0;
3) f(x) = 5x-x2 в точке x = 1; 4) f(x) = ![]() в
точке x = -1; 5) f(x) = sin2x в
точке x =
в
точке x = -1; 5) f(x) = sin2x в
точке x =![]() ;
6) f(x) = cosx
в точке x =
;
6) f(x) = cosx
в точке x = ![]() ;
;
7) f(x) = ![]() в
точке х = 1; 8)
в
точке х = 1; 8) ![]() в
точке х = 5.
в
точке х = 5.
Карточка-инструкция по теме «Правила дифференцирования»
3. Правила дифференцирования
Пусть С- постоянна, u=u(x) и v=v(x) – дифференцируемые функции, х- независимая переменная
|
№ |
Правило вычисления производной |
Примеры |
|
1 |
Производная постоянной функции равна нулю: С'=0 |
(4)'=0; (-2,5)'= 0. |
|
2 |
Производная функции y = x равна 1: x'=1 |
|
|
3 |
Производная функции y = kx равна k: (kx)'= k |
(2х)'=2; (-4,7х)'=-4,7. |
|
4 |
Производная функции y = xn равнаn⋅xn-1: (xn)'= n⋅xn-1 |
(х3)'=3x3-1=3x2; (x-4)'=-4x-4-1= -
4x-5= - |
|
5 |
Производная суммы(разности)
равна сумме (разности) производных: (u |
(x2+5x)'=(x2)'+(5x)'=2x2-1+5=2x+5; (8-x)'=(8)'-(x)'=0-1=-1. |
|
6 |
Производная произведения равна: (u⋅v)'=u'⋅v+u⋅v' |
(x2⋅(9+2x))'=(x2)'⋅(9+2x)+x2(9+2x)'=2x2-1(9+2x)+x2((9)'+(2x)')= =2x⋅(9+2x)+x2∙2=18x+4x2+2x2=18x+6x2. |
|
7 |
Постоянный множитель можно выносить за знак производной: (С⋅u)'=C⋅u' |
(-8x7)'=-8⋅(x)'=-8⋅7x7-1= -56x6. |
|
8 |
Производная частного равна(v≠0): а) |
а) |
|
9 |
Производная сложной функцииh(х)=g(f(х)) равна: h'(x)=g'(f(x)) f '(x) |
а) ((2-3х)4) |
|
10 |
(sinx)'= cosx |
|
|
11 |
(cosx)'= -sinx |
|
|
12 |
(tgх)'= |
|
|
13 |
( |
|
|
14 |
(eх)'= eх |
|
|
15 |
(aх)'=aх⋅ln a |
(3х)'=3х⋅ln 3 |
|
16 |
(lnх)'= |
|
|
17 |
(loga х)'= |
(log2 х)'= |
|
18 |
( |
|
Карточка-инструкция по теме «Уравнение касательной»
4. Уравнение касательной к графику функции у = f(х) в точке (х0; у0)
Уравнение касательной к кривой y = f(x) в точке (х0; у0), принадлежащей этой кривой, имеет вид у - у0 = f '(х0)( х- х0).
Задание. Напишите уравнения касательной к графику функции y = f(x) в точке с абсциссой х0 = 1, если: a) f(x)=x3 + 2x2-5;
б) f(x) = x2e-х
|
№ шага |
План составления уравнения касательной к кривой в заданной на ней точке |
Применение плана |
|
|
|
|
a) f(x) = x3 + 2x2-5 |
б) f(x) = х2е-х |
|
1 |
Вычисляем значение функции у = f(х) в точке х = х0 |
х0=1. у0 = f(1), у0 =1+2-5 = -2 |
х0 = 1, у0 = f(1),
у0=1·e-1= |
|
2 |
Находим производную функции f '(х) |
f '(х)= 3х2 + 4х |
f '(х) = 2хе-e – х2e-x= хе-x (2 -х) |
|
3 |
Вычисляем значение производной в точке х0, т. е. f '(х0) |
f '(х0)= f '(1) = 3 + 4 = 7 |
f (х0)= f '(1)= 1·е-1(2- l) = |
|
4 |
Подставляем числа х0, у0, f '(х0) в уравнение касательной и записываем ответ |
у-(-2) = 7(х-1), у = 7х-7-2, у = 7х-9 |
y- |
Примеры. Применяя указанный выше план, напишите уравнение касательной к графику функции у = f (х) в точке х0, если:
1) f(х) =1- x2,
х0 = 1; 2) f(х) = х2 - 3x + 2, х0 = -1; 3) f(х) =![]() х0
= -1; 4) f(х) =
х0
= -1; 4) f(х) = ![]() ,
х0 = 2; 5) f(х) =
,
х0 = 2; 5) f(х) = ![]() ,
х0= 4;
,
х0= 4;
6) f(х) = sin3x, х0 =![]() ;
7) f(х) = х3 - 2x,
х0 = -1; 8) f(x) = cos2x, x0
=
;
7) f(х) = х3 - 2x,
х0 = -1; 8) f(x) = cos2x, x0
=![]() ;
9) f(х) = ln x, х0 = е.
;
9) f(х) = ln x, х0 = е.
Карточка-инструкция по теме «Признак возрастания (убывания) функции»
5. Признак возрастания (убывания) функции
Если f'(x)![]() на
промежутке I, то f(x) возрастает на I.
на
промежутке I, то f(x) возрастает на I.
Если f'(x)![]() 0
на промежутке I, то f(x) убывает
на I.
0
на промежутке I, то f(x) убывает
на I.
Замечание. Если функция непрерывна на конце промежутка, то его можно присоединить к промежутку возрастания (убывания).
Задание. Найдите промежутки возрастания и убывания функции y = 3x-x3 (здесь и далее имеется в виду все множество точек, в которых функция возрастает (убывает) на естественной области определения)
|
№ шага |
План нахождения промежутков возрастания и убывания функции |
Применение плана |
|
1 |
Найдите область определения функции |
1) D(y) = R. |
|
2 |
Найдите производную |
2) y' =(3-3x2)'=(3х)' –(х3)' = 3 – 3х2 = 3(1 – х2)= 3(1 – х)(1 + х) y'=0; 3(1 – х)(1 + х) = 0 1 – х = 0 или 1 + х = 0 х = 1 х = -1 |
|
3 |
Определите знак производной |
|
|
4 |
По знаку производной найдите искомые промежутки |
4) Функция возрастает на [-1; 1], убывает на [- |
Примеры. Найдите промежутки возрастания и убывания функции: 1) y=3x2 -4x3; 2) y = x3 -3x2 +4; 3) y=x2+5x+9;
4) y=x3-3x+1; 5) y=![]() x3-
x3-![]() x2-2x-5
x2-2x-5
Карточка-инструкция по теме «Экстремумы»
6. Экстремумы
Пусть x0 – критическая точка. Тогда возможны лишь следующие комбинации знаков слева и справа от неё: +-, -+, ++, --. Соответствующие четыре случая проиллюстрированы на рисунках 2- 5.
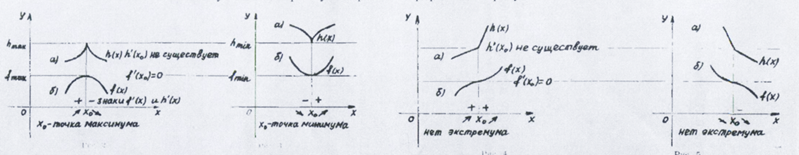
Достаточное условие экстремума: если в точке х0 производная меняет знак с плюса на минус, то х0 – точка максимума; а если с минуса на плюс, то x0 – точка минимума.
Задание. Найдите точки экстремума и экстремумы: y= 3x- x3.
|
№ шага |
План нахождения точек экстремума функции |
Применение плана |
|
1 |
Найдите область определения. |
1)D(y)=R. |
|
2 |
Найдите производную. |
2)y'=3- 3x2 = 3(1- x2) = 3 (1- x) (1+ x). |
|
3 |
Найдите критические точки. |
3) y' = 0, 3(1- x)(1+ x) = 0, x1 = 1, x2 = -1; критические точки: -1 и 1. |
|
4 |
Определите знак производной и по нему точки экстремума. |
x = -1 – точка минимума, x=1 – точка максимума. |
|
5 |
Найдите экстремумы. |
5)y(-1) = -3+ 1 = -2 – минимум, y(1) = 3 – 1 = 2 – максимум. |
Примеры. Найдите точки экстремума и экстремумы функции: 1) y = 3x2 – 4x2; 2) y = x3 – 3x2 + 4; 3) y = x2 + 5x + 9;
4) y = x3 – 3x + 1; 5) y= ![]() x3 -
x3 - ![]() x2 – 2x – 5.
x2 – 2x – 5.
Карточка-инструкция по теме «Наименьшее и наибольшее значения функции»
7. Найдите наименьшее и наибольшее значения функции
Задание. Найдите наименьшее и наибольшее значения функции y=x4 - 2x2 - 3 на промежутке [0; 2].
|
№ шага |
План нахождения yнаим и yнаиб на [a; b] |
Применение плана |
|
1 |
Находим производную функции |
y'=4x3-4x=4x(x2-1) |
|
2 |
Находим критические точки функции |
y'=0, 4x(x2-1)=0 x=0 и x2-1=0 x=-1, x=0 x=1 – критические точки функции |
|
3 |
Выбираем критические точки, лежащие внутри [a; b] |
0 и 1 |
|
4 |
Находим значение функции в критических точках (внутри данного отрезка) и на концах отрезка |
y(1) =1-2-3=-4 y(0) = -3 y(2) = 16-8-3=5 |
|
5 |
Из найденных значений функции выбираем наименьшее и наибольшее |
унаим = y(1) = -4, yнаиб = y(2)=5 |
Примеры. Применяя указанный выше план, найдите
наименьшее и наибольшее значения функции f(x) на промежутке [a; b], если: 1) f(x)=2x2 - 4x+3, [0;4]; 2)f(x)=3x2
- x3, [-1;3]; 3) f(x)=3x3 - 9x2 +2, [-1;1]; 4) f(x)=![]() x3 - 4x,
[0;2]; 5) f(x)=x3-3x2+3x+2; [-2;2]; 6)f(x)=tg x + ctg2x,
x3 - 4x,
[0;2]; 5) f(x)=x3-3x2+3x+2; [-2;2]; 6)f(x)=tg x + ctg2x,![]() ;
7) f(x)=x+cos2(x),
;
7) f(x)=x+cos2(x), ![]() 8)f(x)=2x2-lnx, [1;e]; 9)f(x)=
8)f(x)=2x2-lnx, [1;e]; 9)f(x)=![]() ,[-3;3].
,[-3;3].
Карточка-инструкция по теме «Схема исследования функции»
8. Общая схема исследования функции и построение ее графика
Задание. Исследуйте и постройте графики функции: а) f(x)=
3х4 - 4х3 + 1;
б) f(х) =![]()
|
№ шага |
План исследования функции |
Применение плана |
|
|
а) f(х) = 3х4 - 4х3 + 1 |
б) f(х)
= |
||
|
1 |
Находим область определения функции |
D(f)=R |
х2- 1=0, х= ± 1,
x |
|
2 |
Исследуем функцию на четность, нечетность |
f(-х) = 3х4 - 4х3 + 1 |
f(-х) = |
|
3 |
Находим нули (корни) функции и промежутки ее знакопостоянства |
3х4 - 4х3 + 1 = 0, (х- 1)2 (3x2+ 2х + 1) = 0, х - 1 = 0, х = 1- нуль функции |
|
|
4 |
Находим производную функции и ее критические точки |
у' = (3х4 - 4х3 + 1)' = 12х3- 12х2 = = 12х2 (х - 1) у' = 0, 12х2 (х - 1) = 0, х2 = 0 и х-1= 0, х = 0 и х = 1- критические точки функции |
y'= y'= 0, |
|
5 |
Находим промежутки монотонности, точки экстремума и экстремумы функции |
у' (-1) < 0, у' (0,5) < 0, у (2) > 0, х = 0 - не является точкой экстремума, x = 1 -точка минимума, ymin = y(1) = 0 |
y' (-2)>0, y' (-0,5) > 0, у' (0,5) < 0, у'(2)<0, х = 0 – точка максимума, ymax= y(0) = 0 |
|
6 |
Находим предел функции при х |
|
|
|
7 |
Строим эскиз графика функции |
|
|
Примеры. Исследуйте и постройте графики функций: 1) у = х2
- 3х2 + 2; 2) у = 2х2 - х4 - 1; 3)
у = 6х - х2 - 5; 4) у = ![]() +
+![]() ; 5) у = 3х
- х3;
; 5) у = 3х
- х3;
6) у = х3 -
3х2 + 4; 7) у = x3-3х+1;
8) y = ![]() ; 9) у = x2 +
; 9) у = x2 + ![]()
Карточка-инструкция по теме «Исследование функции»
9. Исследование функций с помощью производной и построение их графиков
Задание. Исследуйте функцию у = 3х – х3 с помощью производной и постройте ее график.
|
№ шага |
План решения |
Применение плана |
|
|
Найдите область определения. |
1) D (y) = R. |
|
1 |
Найдите производную функции |
2) у' =(3х – х3)'= 3-3х2 = 3(1-х) = 3(1-х) (1+х). |
|
2 |
Найдите критические точки. |
3) у' =0, 3(1-х) (1+х) = 0, х1 = -1, х2 = 1; критические точки: - 1; 1. |
|
3 |
Определите знак производной и по нему найдите промежутки возрастания и (убывания) и точки экстремума. |
Функция убывает на (- ∞; - 1] и на [1; + ∞); Функция возрастает на (-1;1). х = -1 – точки минимума; х = 1 – точка максимума. |
|
4 |
Найдите экстремумы и значения функции в дополнительных точках. |
у ( -1) = -3 + 1 = -2 – минимум, у (1) = 3 – 1 = 2- максимум, у (0) = 0, у (2) = 6 – 8 = -2, у (-2) = -6 + 9 = 2. |
|
5 |
Постойте график функции. |
Рисунок
Примечание. Удобно брать Дополнительные точки по мере построения графика. |
Примеры. Исследуйте функции с помощью производной и постройте их графики:
1) у = 3х2 –
4х3; 2) у = х3– 3х2 + 4; 3) у = х2
+ 5х + 9; 4) у = х3 + 1; 5) у = ![]() х3
– 2х.
х3
– 2х.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.