
Teacher Guides of the Lesson
Theoretical material for the lesson, definitions for concepts
ION Experiments to find the mass of an electron first involve finding the charge-to-mass ratio e/me. This is known as the specific charge on the electron – the word ‘specific’ here means ‘per unit mass’. Using the equation for an electron travelling in a circle in a magnetic field, we have e/me= v/Br. Clearly, measurements of v, B and r are needed to measure e/me.

Figure 11.1
There
are difficulties in measuring B and r. For example, it is
difficult to measure r with a rule outside the tube in Figure 11.1 because of parallax error.
Also, v must be measured, and you need to know how this is done. One way
is to use the cathode–anode voltage Vca. This p.d. causes
each electron to accelerate as it moves from the cathode to the anode. If an
individual electron has charge −e then an amount of work e ![]() Vca is done on each electron.
This is its kinetic energy as it leaves the anode: eVca =
Vca is done on each electron.
This is its kinetic energy as it leaves the anode: eVca = ![]() mev 2
mev 2
where me is electron mass and v is the speed of the electron.
Eliminating v from the
two equations eVca = ![]() mev 2 and
mev 2 and
r = mev/Be gives: e/me= 2Vca / r 2B 2
Hence, if we measure Vca, r and B, we can calculate e/me.
As we shall see shortly, the electron charge e can be measured more directly, and this allows us to calculate the electron mass me from the value of e/me.
Electric and magnetic fields
Now we will consider what happens when an electron beam passes through an electric field and a magnetic field at the same time.
Velocity selection
Balancing the effects of electric and magnetic fields is also used in a device called a velocity selector. This is used in devices such as mass spectrometers where it is desired to produce a beam of charged particles all moving with the same velocity. The construction of a velocity selector is
shown in Figure 11.2. Two parallel plates are situated in an evacuated chamber. They provide a uniform electric field of strength E.
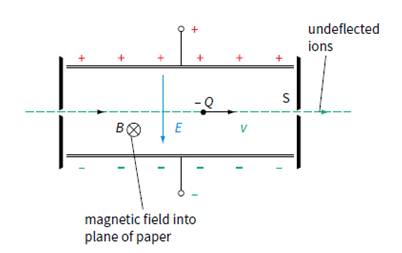
Figure 11.2 A velocity selector – only particles with the
correct combination of charge, mass and velocity will emerge
through the slit S.
The region between the plates is also occupied by a uniform magnetic field of flux density B which is at right angles to the electric field. Charged particles (electrons or ions) enter from the left. They all have the same charge and mass but are travelling at different speeds. The electric force Ee will
be the same on all particles as it does not depend on their speed; however, the magnetic force Bev will be greater on those particles which are travelling faster. Hence, for particles travelling at the desired speed v, the electric and magnetic forces balance and they emerge undeflected from the slit S. If a negative ion has a speed greater than V/Bd the downward magnetic force on it will be greater than the
upward electric force. Thus it will be deflected downwards and it will hit below slit S. Note that we do not have to concern ourselves with the gravitational force mg acting on the charged particles as this
will be much smaller than the electric and magnetic forces.
S
Instructions for demonstrations and safety
Warning: experiments with electricity should be performed under the supervision of teachers or adults familiar with electricity safety procedures.
Additional guidelines for organizing a lesson
1. Organization moment. Establishing emotional state. Checking for absent students.
2. Teacher introduces the topic and objectives of the lesson, assess criteria.
3. Teacher reminds learners about the bubble chamber photograph which was shown in a previous lesson and asks to share their knowledge about the importance of finding of the speed of the particle and radius of its path, then the specific charge/the ratio of charge to mass can be found.
4. Teacher asks learners to divide into two groups and research tasks: the charge-to-mass ratio of an electron and velocity selection of charged particles.
5. Teacher suggests students to answer the Test Yourself questions. Individual students were called on to respond to questions and share their own opinions/thoughts.
6. Teacher asks learners to do set of calculations based on the velocity selector can be used to assess understanding of the underlying principles and use of equations.
7. At the end of the lesson students are encouraged to reflect on what they have learned and
what they need to improve.
Recommendations for formative assessment
Activity1. Students discuss learning objectives and assess criteria.
Activity2. Students share their knowledge with a teacher about the importance of finding of the speed
of the particle and radius of its path then the specific charge.
Activity3. Learners are divided into two groups and research tasks: the charge-to-mass ratio of an
electron and velocity selection of charged particles. The results of group works should be
given in the form of presentations to be defended by learners. Assessment criteria should be
agreed in advance.
Activity4. Students answer the Test Yourself questions. Individual students are called on to respond to
questions and share their own opinions/thoughts.
Activity5. Learners do set of calculations based on the velocity selector can be used to assess
understanding of the underlying principles and use of equations.
Activity6. At the end of the lesson students are encouraged to reflect on what they have learned
and what they need to improve.
Answers, criteria for assignments, additional materials for the lesson
Activity 4
Answer
a. Magnetic force - upwards and electric force – downwards;
b. v =1.5 ∙ 103 V m−1 / 0.30 T = 5 km/s
c. If a positive ion has a speed greater than in b, the downward electric force on it will be greater
than the downward magnetic force. Thus it will be deflected downward and it will hit below slit S.
Activity 5
Answer
1 a Ek = 15 ´ 103
´ 1.6 ´ 10-19 = 2.4 ´ 10-15 J (1 eV = 1.6 ´ 10-19 J) [1]
![]() mv2 = 2.4 ´ 10-15
mv2 = 2.4 ´ 10-15
v = ![]() [1]
[1]
v = 1.68 ´ 106 m s-1 » 1.7 ´ 106
m s-1 [1]
b F
= ma = ![]() [1]
[1]
F = ![]() [1]
[1]
F =
9.60 ´ 10-14 N » 9.6 ´ 10-14 N [1]
c F
= BQv [1]
B = ![]() =
= ![]() [1]
[1]
B » 0.36 T [1]
d speed
= ![]()
time = ![]() =
= ![]() [1]
[1]
time = 1.87 ´ 10-7 s » 1.9 ´ 10-7 s [1]
2 a In order for the
positively charged ions to emerge from the slit,
the net force perpendicular to the velocity must be zero. [1]
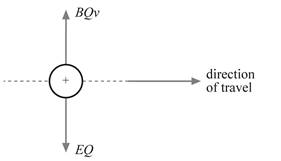
electrical force on ion = magnetic force on ion [1]
EQ = BQv [1]
The charge Q cancels.
E = Bv [1]
The electric field
strength is E = ![]() . Therefore, the
magnetic flux density is:
. Therefore, the
magnetic flux density is:
B = ![]() =
= ![]() =
= ![]() [1]
[1]
B = 3.47 ´ 10–2 T » 35 mT [1]
List of useful links and literature
Douglas C. Giancoli, Physics Principles with Applications, Seventh edition 2014.
David Sang, Graham Jones, Gurinder Chadha and Richard Woodside, Cambridge International
AS and A Level Physics Course book Second Edition, 2014
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.