Поделиться
1Дидактикалық материал 1Жұптық жұмыс.docx
Жұптық жұмыс
1. Арифметикалық прогрессияның тоғызыншы мүшесін екінші мүшесіне бөлгенде бөліндінің мәні 5-ке тең, ал осы прогрессияның он үшінші мүшесін алтыншы мүшесіне бөлгенде 2 шығады және қалдық 5 болады. Прогрессияның бірінші мүшесін және айырмасын табыңыз.
2. Арифметикалық прогрессияның алғашқы а1, а2, а3 мүшелерін табыңыз, егер а1 + а3 +а5 = - 12 және а1 .a3 .a5=80 тең болса.
Бағалау критерийлері мен шешімдері:
1.
|
Бағалау критерий |
дескриптор |
балл |
|
есептер шығару барысында арифметикалық прогрессияның n-ші мүшесінің формуласын қолданады |
жүйенің бірінші теңдеуін құрастырады |
1 |
|
жүйенің екінші теңдеуін құрастырады |
1 |
|
|
|
1 |
|
|
|
1 |
Шешуі:
Барлық қиындық екінші теңдеуді құрастыруда болады.
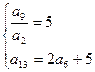
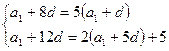
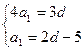
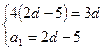
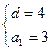
Жауабы: 
, 
2.
|
Бағалау критерий |
дескриптор |
балл |
|
есептер шығару барысында арифметикалық прогрессияның n-ші мүшесінінің формуласын қолданады |
жүйенің бірінші теңдеуін құрастырады |
1 |
|
жүйенің бірінші теңдеуін құрастырады |
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
Шешуі : Есептің шартынан:
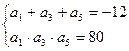
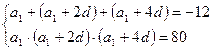
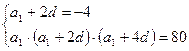
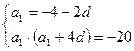
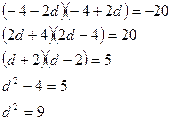
d= -3, a1=2, a2= -1, a3= - 4
d=3, a1= - 10, a2= - 7, a3= - 4
Жауабы: 2; -1; -4 немесе -10; -7; -4
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
