1Теорема Гаусса._Материал для Учителя

Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.

Поток вектора напряженности

Зададим новую физическую величину, описывающую электрическое поле – поток Φ вектора напряженности электрического поля. Предположим, что в пространстве, содержащем заданное электрическое поле, имеется некая достаточно малая площадка ΔS

Элементарный поток вектора напряженности (через площадку S) – это физическая величина, равная произведению модуля вектора , площади ΔS и косинуса угла αмежду вектором и нормалью к площадке:

ΔΦ=EΔScos α=EnΔS..

В данной формуле En является модулем нормальной составляющей поля .

.

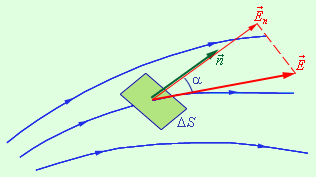
Рисунок 1. Иллюстрация элементарного потока ΔΦ.

Теперь возьмем для рассмотрения некую произвольную замкнутую поверхность S. Разобьем заданную поверхность на площадки небольшого размера ΔSi, рассчитаем элементарные потоки ΔΦi поля через эти малые площадки, после чего найдем их сумму, что в итоге даст нам поток Φ вектора через замкнутую поверхность S (рис.  2):

Φ=∑ΔΦi=∑EmΔSi

Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.

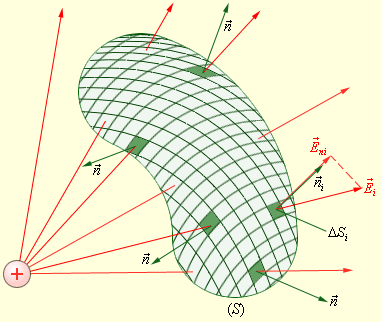
Рисунок 2. Расчет потока Ф через произвольную замкнутую поверхность S.

Теорема Гаусса.

Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.

Поток вектора напряженности электростатического поля  через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную .

Уравнение Гаусса имеет вид: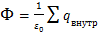

Для доказательства рассмотрим сначала сферическую поверхность S, в центре которой находится точечный заряд q. Электрическое поле в любой точке сферы перпендикулярно к ее поверхности и равно по модулю 

где R – радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4πR². Следовательно,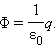 

Окружим теперь точечный заряд произвольной замкнутой поверхностью S и рассмотрим вспомогательную сферу радиуса R₀ (рис. 3).

Рассмотрим конус с малым телесным углом ΔΩ при вершине. Этот конус выделит на сфере малую площадку ΔS₀, а на поверхности S – площадку ΔS. Элементарные потоки ΔΦ₀ и ΔΦ через эти площадки одинаковы. Действительно, 

Здесь ΔS' = ΔS cos α – площадка, выделяемая конусом с телесным углом ΔΩ на поверхности сферы радиуса n.

Так как  а  следовательно  Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ₀ через поверхность вспомогательной сферы: 

Аналогичным образом можно показать, что, если замкнутая поверхность S не охватывает точечного заряда q, то поток Φ = 0. Такой случай изображен на рис. 1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, поэтому в этой области силовые линии не обрываются и не зарождаются.

Обобщение теоремы Гаусса на случай произвольного распределения зарядов вытекает из принципа суперпозиции. Поле любого распределения зарядов можно представить как векторную сумму электрических полей  точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S будет складываться из потоков Φ_i электрических полей отдельных зарядов. Если заряд q_i оказался внутри поверхности S, то он дает вклад в поток, равный  если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.

Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).

Применение теоремы Гаусса

В качестве примера можно рассмотреть задачу, в которой необходимо вычислить поле тонкостенного полого однородно заряженного длинного цилиндра с радиусом R. Такая задача имеет осевую симметрию, и из соображений симметрии электрическое поле должно иметь направление по радиусу. Таким образом, чтобы иметь возможность применить теорему Гаусса, оптимально выбрать поверхность замкнутого типа S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов (рис. 4).

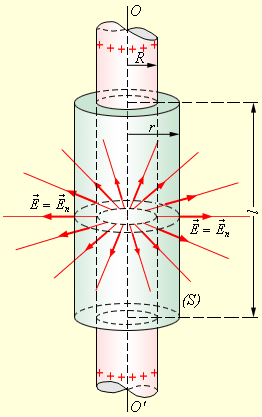
Рисунок 4 Иллюстрация поля однородно заряженного цилиндра. OO' – ось симметрии.

Если rR, то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2πrl. Применим закон Гаусса и получим: 

Φ=E2πrl=

В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:

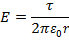
Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.

Чтобы найти напряженность поля внутри заряженного цилиндра, необходимо создать замкнутую поверхность для случая r<R. В соответствии с симметрией задачи поток вектора напряженности через боковую поверхность цилиндра должен быть, и в этом случае он равен Φ=E2πrl. Исходя из гауссовской теоремы, этот поток находится в пропорции к заряду, расположенному внутри замкнутой поверхности. Заряд этот равен нулю, откуда вытекает, что электрическое поле внутри однородно заряженного длинного полого цилиндра тоже есть нуль.

Скачано с www.znanio.ru