Поделиться
2Дидактикалық материал 2 Жеке өзіндік жұмыс.docx
Жеке өзіндік жұмыс
А деңгей
1. 
арифметикалық
прогрессияның әріптермен белгіленген мүшелерін табыңыз:
|
Бағалау критерий |
дескриптор |
балл |
|
есептер шығару барысында арифметикалық прогрессияның сипаттамалық қасиетінің формуласын қолданады; |
арифметикалық
прогрессияның сипаттамалық қасиетінің формуласы
арқылы белгісіз |
1 |
|
арифметикалық
прогрессияның сипаттамалық қасиетінің формуласы
арқылы белгісіз |
1 |
|
|
арифметикалық прогрессияның айырмасын табады |
1 |
|
|
арифметикалық
прогрессияның сипаттамалық қасиетінің формуласы
арқылы белгісіз |
1 |
Шешуі:
Арифметикалық прогрессияның сипаттамалық қасиеті бойынша:
Жауабы: 
В деңгей
1. Үш
функция берілген 
, 
,
.
сандары көрсетілген ретпен
шектеулі арифметикалық прогрессия құрайтындай болатын
t-нің мәнін табыңыз. Осы сандарды табыңыз.
|
Бағалау критерий |
дескриптор |
балл |
|
есептер шығару барысында арифметикалық прогрессияның сипаттамалық қасиетінің формуласын қолданады; |
арифметикалық
прогрессияның сипаттамалық қасиетінің формуласы
арқылы белгісіз |
1 |
|
арифметикалық прогрессияның
сипаттамалық қасиетінің формуласы арқылы белгісіз |
1 |
|
|
арифметикалық
прогрессияның сипаттамалық қасиетінің формуласы
арқылы белгісіз |
1 |
Шешуі:
Арифметикалық прогрессияның сипаттамалық қасиетін қолданамыз:
- арифметикалық прогрессия,
егер 
- ортанғы мүшесі болса,
онда 
.
, 
,
Жауабы:
С деңгей
1.
сандары келесі шарттарды
қанағаттандырады:
.
сандары көрсетілген ретпен
арифметикалық прогрессия құрайтынын дәлелдеңіз.
|
Бағалау критерий |
дескриптор |
балл |
|
есептер шығару барысында арифметикалық прогрессияның сипаттамалық қасиетінің формуласын қолданады; |
арифметикалық
прогрессияның сипаттамалық қасиетінің формуласы
арқылы |
1 |
|
пропорцияның қасиетін қолданады |
1 |
|
|
өрнекті ықшамдайды |
1 |
|
|
|
1 |
Шешуі:
Арифметикалық прогрессияның
сипаттамалық қасиетін қолданамыз: 
Үш сан арифметикалық прогрессия құрайды, егер осы қасиет орындалса:
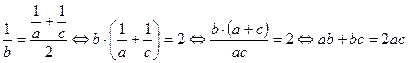
Осыдан сандары
арифметикалық прогрессия құрайды.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
