
Қосымша
Жарты бұрыштың тригонометриялық функциясының формулаларын қорытып шығарыңыз.
Ол үшін қосбұрыштың косинусының формуласын қолданыңыз.
Қосбұрыштың косинусының
формуласын ![]() пайдаланып
пайдаланып
![]() ның орнына
ның орнына ![]() – ні қойып,
– ні қойып, ![]() =
=![]() немесе
немесе
![]() =
=![]() (1)
(1)
теңдігін аламыз.
![]() бұрышы үшін бізге
белгілі негізгі тригонометриялық тепе-теңдікті жазамыз:
бұрышы үшін бізге
белгілі негізгі тригонометриялық тепе-теңдікті жазамыз:
![]() (2)
(2)
Енді (1) және (2) теңдіктерін мүшелеп қоссақ,
![]() , бұдан
, бұдан ![]() шығады.
шығады.
(2) теңдіктен (1) теңдікті мүшелеп алғанда
![]() , бұдан
, бұдан ![]() шығады.
шығады.
Демек, жартыбұрыштың косинусы мен синусының формулаларының жалпы түрі:
![]() (3)
(3)
![]() (4)
(4)
Жартыбұрыштың тангенсі мен котангенсінің формулаларын өз беттеріңмен шығарып көріңіздер.
![]() (5)
(5)
![]() (6)
(6)
1. ![]() және
және ![]() екені
белгілі.
екені
белгілі. ![]() cos
cos![]() , tg
, tg![]() -ні табыңыз.
-ні табыңыз.
Шешуі. ![]() және
берілген ширекті қолданып,
және
берілген ширекті қолданып, ![]() -нің мәнін
табайық, яғни
-нің мәнін
табайық, яғни ![]() .
.
![]() болғандықтан,
болғандықтан,
![]() , яғни ІІ ширекте жатыр.
, яғни ІІ ширекте жатыр.
Сондықтан
![]() .
.
![]() .
.
Енді ![]() -нің мәнін екі
тәсілмен табуға болады:
-нің мәнін екі
тәсілмен табуға болады:
1) ![]() =
= 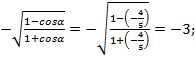
2) 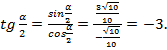
Жауабы: ![]() ,
, ![]() ,
, ![]()
![]() өрнегін
өрнегін ![]() және
және
![]() арқылы өрнектейміз,
сонда
арқылы өрнектейміз,
сонда
![]() , өйткені
, өйткені ![]() немесе
немесе
![]() , өйткені
, өйткені ![]()
Демек,
![]() (7)
(7)
![]() (8)
(8)
2. ![]() -дің мәнін табыңыз.
-дің мәнін табыңыз.
Шешуі. 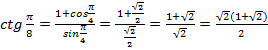 .
.
Жауабы: ![]()
3. ![]() тепе-теңдігінің
ақиқаттығын дәлелдеңіз.
тепе-теңдігінің
ақиқаттығын дәлелдеңіз.
Дәлелдеуі. ![]()
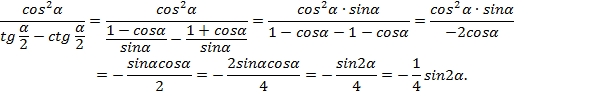
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.