АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ КОМАНДЫ.docx

АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ КОМАНДЫ

Как мы уже говорили ранее, группа арифметических и логических команд состоит из таких команд, которые требуют вы- полнения некоторых арифметических операций, логических или операций сдвига. В этом разделе мы познакомимся с этими ко- мандами более подробно.

Логические операции. В первой главе логические операции AND (И), OR (ИЛИ) и XOR (исключающее ИЛИ) были представлены как операции, которые комбинируют значения двух входных двоичных разрядов в целях получения одного двоичного разряда на выходе. Эти операции могут быть расширены, т.е. они могут рассматриваться как операции, комбини- рующие значения двух строк битов для получения одной строки битов на выходе, что достигается посредством применения соответствующей базовой операции к отдельным позициям в строках. Например, результат применения операции AND к строкам битов 10011010 и 11001001 будет следующим.

10011010

AND

10001000

Другими словами, при выполнении этой строковой операции результат операции AND для двух битов в каждой пози- ции исходных строк просто записывается в этой же позиции строки результата. Аналогичным образом при выполнении опе- раций OR и XOR с теми же входными строками битов будут получены следующие результаты.

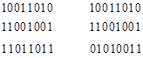OR                     XOR

Операции AND чаще всего используются для помещения нулей в некоторую часть битовой комбинации (не затрагивая при этом другую ее часть). Например, давайте посмотрим, что произойдет, если байт 00001111 использовать в качестве пер- вого операнда логической операции AND. Даже не имея никакой информации о втором операнде, можем сразу же сделать вывод, что четыре старших бита строки результата всегда будут равны 0. Более того, можно также заранее утверждать, что четыре младших бита строки результата будут копиями соответствующих битов второго операнда, что непосредственно под- тверждается следующим примером.

00001111

AND

00001010

Подобное применение операции AND является примером процедуры, называемой маскированием (masking). Первый операнд, или маска (mask), определяет, какая часть другого операнда подвергается изменению. В случае операции AND ре- зультатом маскирования будет частичная копия второго операнда, в которой нули заполняют те позиции, которые не подле- жат дублированию.

Такая операция полезна при работе с битовыми отображениями (bit map), т.е. строкой битов, в которой каждый бит представляет наличие или отсутствие определенного объекта. Мы уже встречались с битовыми отображениями при изуче- нии растрового представления изображений, в котором каждый бит ассоциируется с отдельным пикселем. Другим примером может служить 52-разрядная битовая строка, в которой каждый бит ассоциируется с некоторой игральной картой. Данное представление может использоваться для описания карт, которые были сданы игроку в покер. В этой строке битов в единич- ном состоянии будут находиться только те пять битов, которые ассоциируются с картами, полученными игроком при разда- че, все остальные биты будут иметь значения 0. Аналогичная 52-разрядная битовая строка, в которой уже 13 битов будут равны 1, может представлять отдельного игрока в бридж, тогда как 32-разрядная битовая строка может представлять 32 вида мороженого, выпускаемого изготовителем.

Предположим, что восьмиразрядная ячейка памяти используется как битовое отображение и мы хотим убедиться, что объект, представленный третьим битом со старшего конца, имеется в наличии. Для этого достаточно выполнить операцию AND, использовав в качестве операндов весь байт битового отображения и маску 00100000. В результате будет получен байт, содержащий все нули тогда и только тогда, когда третий со старшего конца бит исходного отображения равен 0. В этом случае в программе можно предпринять необходимые действия посредством помещения после данной команды AND соответствующей команды условного перехода. Если же третий со старшего конца бит растрового изображения равен 1, а нам требуется изменить его значение на 0 без изменения состояния других битов, достаточно выполнить операцию AND, используя в качестве операндов весь байт с битовым отображением и маску 11011111, а затем записать результат в ту ячей- ку, где хранился исходный байт битового отображения.

Если операция AND может использоваться для дублирования части битовой строки с помещением нулей во все биты другой ее части, то операция OR может применяться для дублирования части строки с помещением во все ее оставшиеся биты единиц. Для этого также используется определенная маска, но на этот раз те позиции, значения которых должны быть продублированы, отмечаются в ней нулями, а единицами заполняются все остальные позиции, не подлежащие дублирова- нию. Приведем пример. При выполнении операции OR с любым байтом и битовой комбинацией 11110000 будет получен результат, в котором четыре старших бита всегда будут содержать единицы, тогда как младшие биты будут просто копиями битов исходного операнда, что демонстрируется следующим примером.

11110000

OR

11111010

Таким образом, если операция AND с маской 11011111 может использоваться для того, чтобы поместить значение 0 в третий со старшего конца бит некоторого восьмиразрядного битового отображения, то операция OR с маской 00100000 мо- жет применяться для установки этого же бита в единицу.

Операция XOR чаще всего используется для создания строки дополнения к некоторой строке битов. Например, обрати- те внимание на взаимосвязь между вторым операндом и строкой результата.

11110000

XOR

01010101

Операция XOR между любым байтом и байтом, содержащим все 1, дает в результате байт дополнения к исходному байту.

Операции сдвига. Операции сдвига и вращения (циклического сдвига) позволяют перемещать биты в регистре и часто используются для решения проблем выравнивания, например при подготовке значения байта к последующим операциям маскирования или манипулирования значением мантиссы в представлениях с плавающей точкой. Классификация этих опе- раций производится по направлению движения (вправо или влево), а также с учетом того, является сдвиг циклическим или нет. В рамках этой классификации существует множество различных вариантов, для обозначения которых используется смешанная терминология. Давайте бегло ознакомимся с основными принципами, положенными в ее основу.

Возьмем для примера некоторый байт и сдвинем его содержимое на один бит вправо или влево. На том конце байта, в направлении которого происходит сдвиг, крайний бит выйдет за его пределы и будет потерян, на другом конце образуется пустое место, в которое потребуется ввести некоторое значение. То, что произойдет с удаляемым битом и что будет вставле- но в освободившуюся позицию – именно это и определяет отличия между множеством разнообразных операций сдвига. Од- ним из возможных решений является помещение бита, удаляемого с одного конца байта, в пустую позицию на другом его конце. В результате мы получим циклический сдвиг, который также иногда называют вращением. Если выполнить цикличе- ский сдвиг байта вправо восемь раз подряд, то получим ту же битовую комбинацию, которая существовала вначале, тогда как семь циклических сдвигов вправо идентичны одному циклическому сдвигу влево.

Другим вариантом решения является удаление бита, выходящего за пределы байта, и помещение в освобождающиеся позиции исключительно значения 0. Подобный вариант называют логическим сдвигом (logical shift). Этот вариант сдвига влево можно использовать для умножения значения байта в дополнительном двоичном коде на число 2. В любом случае сдвиг двоичных цифр влево означает умножение значения на 2, подобно тому как и аналогичный сдвиг десятичных цифр означает умножение на десять. Кроме того, сдвинув двоичную строку вправо, можно выполнить деление ее значения на два. Однако в этом случае нужно обязательно сохранить тот знаковый бит, который используется в данной нотации. Для этого часто используется такой вариант сдвига вправо, при котором освобождающаяся позиция (а это, чаще всего, и будет знако- вый бит) всегда заполняется тем значением, которое в ней находилось до операции сдвига. Сдвиги, которые не изменяют значения знакового бита, иногда называют арифметическими (arithmetic shift).

Арифметические операции. Несмотря на то что выше уже шла речь об арифметических операциях сложения, вычита- ния, умножения и деления, все же необходимо сделать ряд замечаний. Как уже говорилось, все операции этой группы чаще всего могут быть реализованы с помощью единственной операции сложения и действия отрицания. Поэтому некоторые ма- логабаритные компьютеры содержат в своем наборе команд только операции сложения или сложения и вычитания.

Кроме того, следует напомнить, что существует множество различных вариантов любой арифметической операции. Речь об этом уже шла выше в связи с операциями сложения, которые включены в набор команд гипотетической машины, описанной в приложении В. При операциях сложения операнды могут быть представлены в двоичном дополнительном коде, и тогда операция их сложения будет выполняться как обычное двоичное суммирование. Если же операнды будут представ- лены как числа в формате с плавающей точкой, то при суммировании потребуется выделить мантиссу каждого из чисел. По- сле этого эти значения должны быть сдвинуты вправо или влево в зависимости от значения в поле порядка. Затем проверяют- ся знаковые биты и выполняется операция сложения. Полученный результат вновь переводится в формат с плавающей точкой.  Как видите, хотя обе описанные выше операции считаются операциями сложения, действия машины по их выполнению будут существенно отличаться. Более того, с точки зрения самой машины, между этими двумя операциями вообще нет никакой связи.

Вопросы для самопроверки

1.  Выполните приведенные ниже операции:

а) AND 010011011 ; б) AND 10000011 ; в) AND 11111111 ;

101001011

11101100

00101101

г) OR 010011011 ;     д) OR 10000011 ;     е) OR 11111111 ;

101001011

11101100

00101101

ж) ХOR 010011011 ; з) ХOR 10000011 ; и) ХOR 11111111 .

101001011

11101100

00101101

2.  Предположим, что требуется выделить средние три бита в семиразрядной строке посредством помещения нулей в ос- тавшиеся ее четыре бита, не изменяя значения трех выделяемых битов. Какую маску и операцию следует использовать в этом случае?

3.  Предположим, что нужно заменить значение средних трех битов в семиразрядной строке на обратное, не изменяя при этом значения оставшихся четырех битов. Какую маску и операцию следует использовать в этом случае?

4.   а) Предположим, что была выполнена операция XOR с первыми двумя битами некоторой строки битов, а затем эта операция последовательно выполнялась с очередным результатом и следующим битом строки. Как общий результат связан с количеством единиц в исходной строке битов?

б) Какое отношение приведенная выше задача имеет к определению требуемого значения бита четности при кодирова- нии сообщения?

5.  Иногда удобнее использовать логическую операцию вместо цифровой. Например, логическая операция AND комби- нирует значения двух битов по тому же принципу, что и операция умножения. Какая логическая операция почти идентична операции сложения двух битов? Какие отличия существуют между этими операциями?

6.  Какую логическую операцию и в сочетании с какой маской следует использовать для преобразования строчных букв в прописные в коде ASCII?

7.  Каков будет результат при выполнении циклического сдвига вправо на три позиции для каждой из следующих бито- вых комбинаций:

а) 01101010; б) 00001111; в) 01111111.

8.  Каков будет результат при циклическом сдвиге влево на одну позицию для каждой из следующих битовых комбина- ций, представленных в шестнадцатеричной системе счисления:

а) АВ; б) 5С; в) В7; г) 35.

9.   На сколько разрядов влево нужно сдвинуть восьмиразрядную строку, чтобы результат был эквивалентен цикличе- скому сдвигу этой же строки вправо на три бита?

10.  Какая комбинация битов будет представлять сумму значений 01101010 и 11001100, если считать, что эти значения представляют числа в формате с плавающей точкой, речь о котором шла в главе 1?

11.   Используя машинный язык, описываемый в приложении В, напишите программу, которая поместит единицу в старший бит ячейки памяти с адресом А7, оставив значения всех остальных битов этой ячейки без изменения.

12.   Используя машинный язык, описываемый в приложении В, напишите программу, которая скопирует значения че- тырех средних битов ячейки памяти с адресом Е0 в младшие четыре бита ячейки памяти с адресом Е1, при этом в старшие четыре бита этой ячейки должны быть занесены нули.