Демоверсия полугодовой контрольной работы по алгебре 10 класс

Вариант 1.

Часть 1.

1. Найдите область определения функции у = . В ответ укажите наименьшее целое число из области определения функции.

2.Найдите по графику наименьшее значение функции: y=sin x на [π/3;7π/6]

3.Найдите значение функции: у =2 sin x + cos x, если х = - π/2.

4.Решите уравнение: - cos x= 3х-1.

5.Сколько корней имеет уравнение: cos x=22 на  [-π;3π].

6.Вычислите: sin (arccos x+ arccos(- x)).

7.Вычислите: sin(-7π)+2 cos31π/3 - tg7π/4.

8.Найдите значение выражения: 17 sinα -15, если cos α=  и  π/2 <α< π.

9. Выберите верные утверждения.

1) Если прямая АВ лежит в плоскости и точка С принадлежит прямой АВ, то прямая АС лежит в плоскости .

2)Если прямая  АВ лежит в плоскости , а прямая СД пересекает АВ, то СД лежит в плоскости .

3)Если прямые АВ и СД пересекаются в точке О, то точка Д лежит в плоскости АОС.

4)Если прямые АВ и СД не пересекаются, то прямая АС лежит в плоскости АВС.

10.Найдите сумму наибольшего отрицательного и наименьшего положительного корней уравнения

 4 cos² 2х =2.

11. Сколько корней имеет уравнение  cos х +sin х =0 на [0; π].

Часть 2.

12.Найдите значение выражения  3 tg² х₀ -1, где х₀ – наименьший положительный корень уравнения    2 cos² х + 5 sin x -4=0.

13. Упростите выражение:  .   

14. Через конец М отрезка МN проведена плоскость . Через точку К – середину отрезка МN, и точку N проведены параллельные прямые, пересекающие плоскость  в точке К₁ и N₁ соответственно. Найдите NN₁, если КК₁ меньше NN₁  на 8,4 см.

15.  Решите уравнение:  (2 cos x -1) (4x²- 7 х+5) = 0.

Вариант 2.

Часть 1.

1.Найдите  область определения функции: у = . В ответ укажите наибольшее целое число из области определения функции.

2.Найдите по графику наибольшее значение функции: y= cos x на [π/2;4π/3]

3. Найдите значение функции: у =2 cos (x- π/2)-1, если х = - π/2.

4. Решите уравнение:   cos x= 2х + 1.

5.Сколько корней имеет уравнение:  sin x=- 22 на  [-π;2π].

6.Вычислите: cos (arcsin x+ arcsin(- x)).

7.Вычислите: cos(-9π)+2 sin(-49π/6) - ctg(-21π/4).

8.Найдите значение выражения: 7 - 13 sinα, если cos α =  и π <α< 3π/2.

9. Выберите верные утверждения.

1)Если прямая КМ лежит в плоскости , а прямая NL  пересекает КМ , то NL лежит в плоскости .

2)Если прямая КL лежит в плоскости  и точка М принадлежит КL, то прямая LМ лежит в плоскости .

3)Если прямые КL и NМ не пересекаются, то прямая КМ лежит в плоскости  КLМ.

4)Если прямые КL и NМ пересекаются в точке О, то точка N лежит в плоскости КОМ.

10.Найдите сумму наибольшего отрицательного и наименьшего положительного корней уравнения

 4 sin² 2х =3.

11. Сколько корней имеет уравнение  cos х = sinх  на [0; π].

Часть 2.

12.Найдите значение выражения  5 tg² х₀ + 2,3 ,  где х₀ – наименьший положительный корень уравнения    6 - 6 cos х -  sin² x =0.

13. Упростите выражение:  

14. Через конец А отрезка АВ проведена плоскость . Через точку С-середину отрезка АВ, и точку В проведены параллельные прямые, пересекающие плоскость  в точках С₁ и В₁ соответственно. Найдите ВВ₁, если ВВ₁ больше СС₁ на 7,8 см.

15. Решите уравнение:  (2cos 2 x - 3) (3x²- 7 х+4) = 0.

Демоверсия полугодовой контрольной работы по алгебре

Часть 1.

1.      Найдите область определения функции: у =

2.      Найдите по графику наибольшее значение функции: y= sin x на [π/4; 2π/3].

3.      Найдите значение функции: у = 1 + 2cos(π/2 + х), если х = π/3.

4.      Решите уравнение:  sin x = .

5.      Сколько корней имеет уравнение:  cos х  = 22 на  [-2π; π].

6.      Вычислите:  sin (arcsin 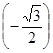 + arctg ).

7.      Вычислить:  tg (-13π/6) + cos(-11π/4) – sin(-7π).

8.      Найдите значение выражения: cosα, если sinα =   и  3π/2 < α<  2π.

9.        Прямая m параллельна прямой n и плоскости . Выберите верное утверждение.

1) Прямая n параллельна плоскости .

2) Прямая n лежит в плоскости .

3) Прямая n лежит в плоскости или параллельна ей.

4) Прямая n пересекает плоскость .                                                                                                                                                                                                                                                                                                                                                                                                                                                                       

10.  Найдите произведение наибольшего отрицательного и наименьшего положительного корней уравнения cos (2х-π/4) = .

11.   Сколько корней имеет уравнение  cos х – sinх = 0  на [-π; π].

Часть 2.

12.  Решите уравнение 2sin²x + cosx + 1 = 0.

13.  Упростите выражение:   .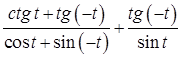

14.  Плоскость пересекает стороны треугольника MNK в точках  P и Q, причем  PQ параллельна MK. Найдите  PN, если PQ: MK = 5:9, MN = 27 см

15.  Решите уравнение:  (2sin(-x/2) – 1)(-2х² + 5х – 2) = 0.