Ю. Н. Макарычев

Н. Г. Миндюк

     Л. Б. Крайнева дидактические материалы ЛГЕБРА

КЛАСС

у 77—-3

ПРОСВЕЩЕНИЕ

И З Д А Т Е Л Ь С Т В О

Ю. Н. Макарычев

Н. Г. Миндюк

Л. Б. Крайнева

	АЛГЕБРА дидактические материалы
	класс

17-е издание

Москва

« Просвещение»

2012

удк 372.8:512 ББК 74.262.21

М15

Макарычев Ю. Н.

М 15 Алгебра. Дидактические материалы. 9 класс / Ю. Н. Макарычев, Н. Г. Миндюк, Л. Б. Крайнева. 17-е изд. — М. : Просвещение, 2012. — 96 с. : ил.

ISBN 978-5-09-026766-3.

Пособие содержит упражнения для самостоятельных работ, которые носят обучающий характер, а также тексты контрольных работ и задания для проведения школьных математических олимпиад.

удк 372.8:512 ББК 74.262.21

Учебное издание

Макарычев Юрий Николаевич

Миндюк Нора Григорьевна

Крайнева Лариса Борисовна

АЛГЕБРА

ДиДактические материалы

9 класс

Зав. редакцией Т. А. Бурмистрова. Редактор Т. Г. Войлокова.

Младший редактор Е. В. Трошко. Художественный редактор О. П. Богомолова. Компьютерная графика И. В. Губиной. Технический редактор и верстальщик И. М. Капранова. Корректоры Т. А. Лебедева, Ю. Б. Григорьева

Налоговая льгота — Общероссийский классификатор продукции ОК 005-93—953000. изд. лиц. Серия ИД М 05824 от 12.09.01. Подписано в печать 17.10.11. Формат 60 х 90 ¹ /16. Бумага офсетная. Гарнитура

Школьная. Печать офсетная. Уч.-изд. л. 4,4. Доп. тираж 20 ООО экз. Заказ № 32949.

Открытое акционерное общество «Издательство «Просвещение». 127521, Москва, 3-й проезд Марьиной рощи, 41.

Отпечатано в ОАО «Саратовский полиграфкомбинат» .

410004, г. Саратов, ул. Чернышевского, 59. www.sarpk.ru

ISBN 978-5-09-026766-3 © Издательство «Просвещение», 2009  Художественное оформление.

Издательство «Просвещение», 2009

Все права защищены

ПРЕДИСЛОВИЕ

Дидактические материалы предназначены для организации самостоятельной работы учащихся и для контроля над их знаниями, умениями и навыками. Они могут использоваться, когда преподавание ведется по учебнику «Алгебра, 9» авторов Ю. Н. Макарычева и др. под редакцией С. А. Теляковского, а также при работе по другим учебникам алгебры 9 класса.

Включенные в данную книгу работы делятся на четыре группы: 1) самостоятельные работы; 2) контрольные работы; З) итоговое повторение по темам; 4) внутришкольные олимпиады.

Самостоятельные работы отмечены индексами С— 1, С—2 и т. д. В книге приведена таблица, в которой указаны номера самостоятельных работ и соответствующие им номера пунктов учебника «Алгебра, 9» Ю. Н. Макарычева и др. 2008 г. и последующих годов издания.

Самостоятельные работы носят обучающий характер. Они представлены в двух вариантах. В каждой работе выделяются два блока заданий. Первый блок, расположенный над чертой, состоит из стандартных тренировочных упражнений. Второй блок включает задания, усложненные по сравнению с заданиями первого блока в алгоритмическом или логическом плане и способствующие развитию учащихся. Каждое упражнение состоит из нескольких заданий, представленных по возрастанию сложности.

Самостоятельные работы достаточно объемны. Они рассчитаны на неоднократное использование. Хорошо успевающим учащимся можно предложить выполнять упражнения второго блока, минуя упражнения первого или часть из них.

Контрольные работы отмечены индексами К—1, К—2 и т. д. Первые восемь работ привязаны к конкретным темам и рассчитаны на один урок. Последняя работа К—9 является повторительной по всему курсу и рассчитана на два урока. Контрольные работы даны в четырех вариантах. В каждую из них включены задания, соответствующие уровню обязательной подготовки, и более сложные задания. Задания обязательного уровня отмечены кружком: • 1, •2 и т. д. С учетом конкретных условий учитель может вносить коррективы в тексты контрольных работ. Для проведения зачета по всему курсу в дидактические материалы включен итоговый тест, составленный в двух вариантах.

Раздел «Итоговое повторение по темам» содержит некоторые теоретические вопросы и упражнения основных видов. Работа с этим материалом может быть организована по-разному: например, можно сочетать фронтальную работу с классом и самостоятельную деятельность учащихся.

Задания олимпиадного характера предназначены для того, чтобы облегчить учителю организацию внутришкольных олимпиад.

З

Таблица использования самостоятельных работ

Самостоятельная работа

Номера пунктов учебника

С—1. Функция. Задание функции формулой С—2. Область определения и область значений функции С—3. График функции С—4. Свойства функции С—5. Квадратный трехчлен и его корни С—б. Разложение квадратного трехчлена на множители 7. Функция у = ах2 , ее график и свойства 8 Графики функций у = ах2 + п и у = а (х — т)2 С—9. Построение графика квадратичной функции С—1О. Функция у = хп С—11. Корень п-й степени С—12. Целое уравнение и его корни С—1З. Уравнения с параметрами С—14. Решение уравнений с помощью разложения на множители и введения вспомогательной переменной С—15. Дробные рациональные уравнения С—16. Решение неравенств второй степени с одной переменной с—17. Решение неравенств методом интервалов с—18. Решение систем неравенств с одной переменной с—19. Уравнение с двумя переменными и его график с—20. Графический способ решения систем уравнений с—21. Решение систем уравнений второй степени С—22. Решение задач с помощью систем уравнений второй степени с—23. Неравенства с двумя переменными с—24. Системы неравенств с двумя переменными с—25. Последовательности с—26. Арифметическая прогрессия. Формула п-го члена с—27. Формула суммы первых п членов арифметической прогрессии С—28. Геометрическая прогрессия. Формула п-го члена С—29. Формула суммы первых п членов геометрической прогрессии С—ЗО. Комбинаторное правило умножения. Перестановки С—31. Различные комбинаторные задачи С—32. Вероятность случайного события

1 1 2 з 4 5 6 7 8 9 12 12 12 13 14 15 14, 15 17 18 19 20 21 22 24 25 26 27 28 31 30—33 35

САМОСТОЯТЕЛЬНЫЕ РАБОТЫ

Вариант

С--1. Функция. Задание функции формулой

1. Найдите:

1)    [ (2), [ (О), f(—1), если f(x) = 12х — 5;

2)    f(10), f(—2), f(O), если f(x) = .х² — 8х;

х-5

З) g(—2), g(2), g(O), если g(x) =           

2. Найдите значение х, при котором функция, заданная формулой

1)    g(x) = 8 — 3х, принимает значение, равное: а) 5; б) 11;

1

2)    f(x) = ——х+2, принимает значение, равное: а) 1; б) 4; з

З. Существует ли значение х, при котором значение функции, заданной формулой f(x) = ' равно: а) 1; 3—х

б) —2,5; в) О? В случае утвердительного ответа укажите это значение.

4. Зная, что

а) f(x) = ^5х2 , найдите f(2) + [ (—2);

2х ³ —5х

                , найдите g(3) + g(—3).

10

5. Известно, что f(x) = Кх + Ь, причем f(2) = 7 и f(3) = 12. Найдите коэффициенты К и Ь.

С--2. Область определения и область значений функции

1. Найдите область определения функции, заданной

формулой:

1) а) f(x) = 19 — 2х;             б) g(x) =

х

в) (Р (х) = х²

5

g(x) = 8 — х2 ,

х 8

в)

2. Укажите область значений функции:

19 - 37х + 1;           6) у = -23;х

З. Найдите область значений функции:

а) f(x) = 5х + 1, где З                 6;

б) g(x) = З — 8х, где —4 х < 2.

4.      Задайте формулой какую-либо функцию, областью определения которой является:

а) множество всех чисел, кроме 2 и З;

б) множество всех чисел, больших или равных 8.

5.      Укажите область определения функции, заданной формулой:

С—3. График функции

1. На рисунке 1 изображен график функции у = f (х), областью определения которой служит промежуток [—3; 4]. Найдите:

1)    г) f(3);

2)    значения аргумента х, при которых:

а)

в) f(x) = —2;

З) наибольшее и наименьшее Рис. 1 значения функции;

4) область значений функции.

у = 0,5х - З;            б) у = -0,5х + 2;	1 в) з
8                                  6	х

х	х	3'
у = х2 ;		y = l x l

2. Постройте график функции:

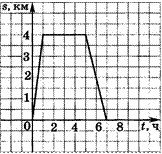З. Рыболов отправился на озеро, а затем вернулся домой. График движения рыболова изображен на рисунке 2. Ответьте на вопросы:

1)    Сколько времени шел рыболов от дома до озера и с какой скоростью?

2)    Сколько времени провел он на озере?

З) Сколько времени затратил рыболов на путь от озера до дома и с какой скоростью он шел?

4)    На каком расстоянии от дома   Рис. 2 находился рыболов через

2 ч? через 5 ч? через 6 ч после выхода из дома?

5)    Сколько времени шел рыболов от озера до шоссе на обратном пути, если известно, что первый раз он пересек шоссе спустя полчаса после выхода из дома?

75
	60
	45
F—t30
		15

4. На рисунке З изображены графики движения велосипедиста (1) и мотоциклиста (П), отправившихся из города в деревню, находящуюся на расстоянии 75 км от города. Пользуясь графиками, ответьте на вопросы:

1)    Кто выехал из города позже и на сколько?

2)    Сколько времени был в пути велосипедист? мотоциклист?

З) Чему равна скорость движения велосипедиста? мотоциклиста?

4)    Кто прибыл в деревню рань-     Рис. З ше и на сколько?

5)    Через сколько часов после своего выезда мотоциклист догнал велосипедиста?

6)    На каком расстоянии от деревни находился велосипедист в тот момент, когда мотоциклист в нее прибыл?

5. Постройте график функции, предварительно заполнив таблицу:

10

где О х 6;

У

7

2,

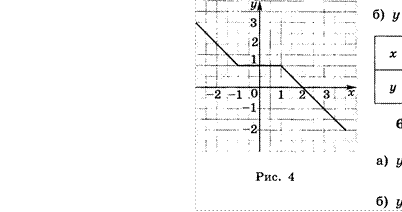
7. Задайте с помощью нескольких формул функцию, график которой изображен на рисунке 4.

х ³ —2х ² — 4х+8

8. Постройте график функции f(x) =

2х ² -8

С--4. Свойства функции

	1
	-1 -2

1. Область определения функции, заданной графиком на рисунке 5, промежуток [—3; З]. Используя график, перечислите свойства функции. Найдите:

1)      а) нули функции; б) промежутки, в которых функция принимает положительные значения, и промежутки, в которых она принимает отрицательные значения;

2)      промежутки, в которых функция возрастает и в которых Рис. 5 она убывает;

З) значение аргумента х, при котором функция принимает наибольшее значение и при котором она принимает наименьшее значение; 4) область значений функции.

2. Выясните свойства функции:

1)    а) у = 28х + 35;    6) у = -0,38х - 19;      в) у = 38;

                 25                                 56

                  х                   

З. Найдите нули функции (если они существуют):

2)    а)

4.                      Постройте график функции f(x) = х + х! и опишите ее свойства.

5.                      Выясните свойства функции

, если х < —2,

2х, если —2 х 2,

, если х > 2.

С--5. Квадратный трехчлен и его корни

1.                      Найдите корни квадратного трехчлена:

1)     а) х 2 — 5х + 6;      в)         - 210 + 14; 2)     а) 2у 2 — у — 6; в) 0,3х2 + 0,1 х; 3)     а) 0,5х2 - х- 0,5; в) -36“ - 12b + 1.

б) —у2 — Зу + 4; г) ЗУ - 12; б) ба2 + 5а + 1; б) —50а 2 + 5а + 1;

2.                      Выделите квадрат двучлена из квадратного трехчлена:

1)    а) х² — 6х + 11; 6) 2у² - 4у - 1; в) а ² — 2а; 2)  б) —х ² —2х+5.

З. Докажите, что при любом у квадратный трехчлен:

а) у² — 4у + 7 принимает положительные значения;

б) —У2 + бу — 12 принимает отрицательные значения.

4.                    При каком значении а квадратный трехчлен:

а) а ² — 10а + 27 принимает наименьшее значение;

б) —а ² — ба — 15 принимает наибольшее значение?

5.                    Имеется прямоугольник со сторонами З и 5 см. Большую его сторону уменьшили на а см, а меньшую увеличили на столько же. При каком значении а площадь полученного прямоугольника окажется наибольшей?

С—б. Разложение квадратного трехчлена на множители

1. Разложите на множители квадратный трехчлен:

	х2 - 7х + 12;	б) 5х 2 — 5х — 10;
	4х 2 — 144;	г) 10х2 + 29х - 30;
	х2 - 2х - 63;	6) 6х 2 + 5х - 4;
в)	17х2 - 425;	г) 5х 2 — 30х + 35.

2. Почему нельзя представить квадратный трехчлен в виде произведения многочленов первой степени:

              6) -2х² + 4х - 7;

2)    а) -е - 10х + 27;    6) -7х² + 6х - 2;

З. Сократите дробь:

а ² — 4

6)

70+14'                             9b+18 х3 + х2 — 72х

6)

        у ² +5у — 14'                9х - 72

4.                    Найдите значение дроби:

1)                                                у ² — 11у — 26 при у — - -5, • 31; 112;

9 у 18

х ² - 18х+80

2)                                                при х —- -12; 8,5; 48.

5х — 50

5. Упростите выражение

                                   80-3          40-270

а + 5 а ² +2а — 15

6. Постройте график функции

х ³ — 2х ² — 4х+8

2х2 - 8

в)

21-зс

5а — а ²

в)

5 + 340 -

С--7. Функция у = ах², ее график и свойства

1.                       Зная, что f(x) = —х ² , заполните таблицу.

аддаадд

Постройте график функции. Найдите: f(—2,5); f(2,5); [ (-3,5); [(3,5).

В той же системе координат постройте график функции g(x) = ——х ². Найдите: (—2,5); g(2,5); (—3,5); 5

(3,5).

2.                       Не выполняя построения, найдите координаты точек пересечения графика функции у = 2х² и прямой:

      а) У = 200;         6) у = 800;

      в) У = 50х;          г) у - -3200х.

З. Принадлежит ли графику функции у = —25х² точка:

      а) А          -100);         6) в (2; 100);          в)

4. Постройте график функции

х ² , если х > 2, у = х, если  2, —х ² , если х < —2.

5. Какова область значений функции (укажите ее наибольшее и наименьшее значения):

1 х ² , где х е [—3; 61; з

1

—х ² , где х Е [—2; 8]?

4

6. Камень, падающий на землю, пролетает за t с расстояние, равное м, где h = g 10 м/с² . Через какое 2 время камень упадет на дно вертикального ствола шахты длиной 120 м?

С--8. Графики функций у= ах² + п

1.                        Используя шаблон параболы у = х ² , постройте график функции:

     а) у = х² — З;                б) у = —х² + 4;        в) у = (х — 2)² ;

2.                        В каких координатных четвертях расположен график функции:

     а)         9х² + 2;          б) у = —5х² + 1;          в) у = —2 (х + 5) ² ?

З. Изобразите схематически график функции:

2

в)

4.    Найдите нули функции (если они существуют):

      а) у = 4х² — 1;          б) у = —3х² + 9;       в) у = —х² — 16.

5.    Постройте график функции:

а) y = lxl -3•,

6.    Постройте график функции:

     а)      б) у=-сх;      в)

С-—9. Построение графика квадратичной функции

1.                        Найдите координаты вершины параболы:

     а) f(x) = х ² — 6х + 4;           б) f(x) = —х² — 4х + 1;

в) f(x) = 3х² - 12х + 2.

      При вычислении воспользуйтесь формулами т = —       и

где т и п — координаты вершины параболы f(x) = ах2 + bx + с.

2.                        Используя результаты вычислений в задании 1а, постройте график функции f(x) = х ² — 6х + 4. Найдите по графику:

а) нули функции; промежутки, в которых f(x) < О и f(x) > О;

б) промежутки убывания и возрастания функции; наименьшее ее значение.

З. Используя результаты вычислений в задании 16, постройте график функции f(x) = —х² — 4х + 1. Найдите по графику:

а) нули функции; промежутки, в которых f(x) < О и f(x) > О;

б) промежутки возрастания и убывания функции; наибольшее ее значение.

4.      Найдите область значений функции у = х² + 6х + 5, где х е [—6; 2].

5.      При каких значениях Ь и с точка М (5; 7) является вершиной параболы у = х² + bx + с?

6.      Мяч брошен вертикально вверх с начальной скоростью 24 м/с. Зависимость расстояния h (м) от мяча до земли от времени полета t (с) выражается формулой .h = 24t — 5t² . Постройте график этой зависимости. Найдите по графику:

1)    какой наибольшей высоты достиг мяч;

2)    в какой промежуток времени он поднимался вверх и в какой опускался вниз;

З) через сколько секунд после броска мяч упал на землю.

С-—10. Функция

1.   Зная, что f(x) = х ¹⁰⁰, сравните:

[(0,125) и [(0,13);

в) f(—O,325) и f

2.   Зная, что g(x) = х¹⁰⁵ , сравните:

(1,023) и (1,13);          6) (-2,7) и «-2,2);

        в) «-4,1) и (4,1);                 г) g(20,8) и g (-21,3);

193);и -0,76).

З. Сколько корней имеет уравнение х = 2500:

а) при четном п; б) при нечетном п?

4.    Решите х^з - -27; г) х⁴ = 625. 8

в) х^а — —81;

125'

5.    Постройте график функции:

г) У = (х + 1)4.

6.    Сколько корней имеет уравнение:

           а) х⁴ = 32х + 5;                   б) х⁴ = 0,5х — 8;

       в) х^з = 32х + 5;            г) х^з = 0,5х - 8?

7.    Принадлежит ли графику функции:

а) у = х⁹ точка А (—2,1; 548,471); точка В (—0,973; -10,8973);

б) у = х⁸ точка С (1,2; 0,98746); точка D (—2,01; 250,4781)?

С--11. Корень п-й степени

1. Найдите значение выражения:

0,16;                 б)

2) а) 6 ³ 0,125;              б) 0,76 в)

6) ⁵ 0,00032 + ³ -0,008;

6) ^з 0,216 - -0,01024;

З. Укажите два последовательных целых числа, между которыми заключено число:

г) 66.

4.    Вычислите:

5.    Решите

в)

г) —х ⁵ + 16= 0.

6.    При каких значениях переменной имеет смысл вы-

ражение:

а) 10в) ⁶ а(а —8);

г) 8 b2 + Ь —12?

7.    Решите уравнение:

       а)         - 31Х ⁵ - 32 = О;         6)        - 82х⁴ + 81 = о;

в) х⁴ + 2х² - 15 = о.

8.    Постройте график функции:

        а) у = Е;           б) у =                               в) у = G; г) у = —45.

Д С--12. Целое уравнение и его корни

1.                       Определите степень уравнения:

а) х⁵ + 3х⁶ - х^з + 1 = О;

в) х² (х + 4) — (х — 2) (х² + 1) = З;

г) (х^з - 2) (3х² + 1) - з (х⁵ - 2) = 4.

2.                       Какие из чисел —3; —2; —1; О; 1; 2; З являются корнями уравнения:

       а) х^з — 4х = О;                   б) х² (х + 1) + (х + 4) = 4;

в) х⁴ - 5х² + 4 = 0?

З. Решите уравнение:

(12х + 1) (3х - 1) - (6х +        = 10; 6)

              6х—1 3х+1       1

в)

4      з          х(2-х) х(3+2х)

г)

                      2                     4

2) а) (6х - 1) (х + 1) = 20;

7) (х + 7) - 11х - зо =

в)

16          8       З х(Зх + 4)

    г) 17 -2х+            = 54

                                           2                    2

4.     Составьте какое-либо

а) первой степени, корнем которого является число 13;

б) второй степени, имеющее корни 4 и —11;

в) третьей степени, имеющее корни —2; 2 и 5.

5.     Решите уравнение: х(х-1) (х-3) ²

а)

           4              2               з          3'

                            2                    4                2

6.     Верно ли утверждение:

а) уравнение х⁶ + 6х ⁴ + 7х ² + 8 = О не имеет корней;

б) уравнение 12х⁵ + 11х³ + 10х — 4 = 140 не имеет отрицательных корней;

в) уравнение 9х (х — 1) — (3х + 4) (3х — 4) = 51 — 9х не имеет корней;

г) уравнение 7х ⁵ + 14х⁴ — 21х² — 49х = 13 не имеет целых корней?

С--13. Уравнения с параметрами

1.                        Найдите:

а) значение с, при котором корнем уравнения З (х - 4) - 5 (х + 2) = сх - б является число 6;

б) значение Ь, при котором одним из корней уравнения 16х ² + 2 (Ь — 4) х + (2 — 36) = О является число 4. Вычислите другой корень.

2.                        При каких целых значениях Ь корень уравнения bx — 1 = О является целым числом?

З. При каких значениях а уравнение 5х — За = 2 имеет:

а) положительный корень;

б) отрицательный корень;

в) корень, больший 10;

г) корень, принадлежащий промежутку (1; 2)?

4.      При каких значениях Ь имеет два корня уравнение:

            а) 4х ² + 8х + ь = о;                  б) 5х² + bx + 5 = О?

5.      При каких значениях t имеет один корень уравнение:

          а) 2х ² — 6х + t = О;                  б) х² + tx + 4 = О?

6.      При каких значениях с не имеет корней уравнение:

7.      Найдите целые значения а, при которых корень уравнения а (х + 1) = 5 является положительным числом.

8.      Из данных уравнений выделите те, которые при любом значении Ь имеют два корня:

х² + bx = О, .r² — bx — 5 = О, х² + bx + 5 = О, х² — 2b = О, Ьх² - 2 = 0, х² -  о.

9.      Найдите, при каких значениях п корнями уравнения х² + п² (х — 1) — х = О являются два противоположных числа.

10.  При каких значениях а уравнение х ² — 2ах + а² — 1 = О имеет два различных корня, принадлежащие промежутку

С--14. Решение уравнений с помощью разложения на множители и введения вспомогательной переменной

1. Решите уравнение:

1)    а) 9х³ - 27х ² = О;    6) х^з - 64х = о;

в) х^з + 0,8х = о;

2)    а) х^з - 4х² - 9х + 36 = О;   6) + 3х⁴ - - 3 = о;

в) у ^з — 2у ² = у — 2.

2. Решите уравнение, используя введение новой переменной:

а) (х² -        - 4(х² - 7) - 45 = о; 6) (х² + 2х)² - 2 (х² + 2х) - З = О;

в) (х² — х + 1) (х² — х — 7) = 65.

З. Решите биквадратное уравнение:

            а) х⁴ - 13х ² + 36 = О;                    г) х⁴ + 7х² - 44 = о;

          б) х ^а — 5х² + 4 = О;                       д) х^а + 9х² + 8 = О;

           в) х⁴ + 5х² — 6 = О;                       е) х⁴ + 16х² = О.

4.                   Найдите координаты точек пересечения с осью абсЦИСС графика функции у = х⁴ — 8х² — 9.

5.                   Решите уравнение

Х⁵ + Х⁴ + 3Х³ + 3Х ² + 2Х + 2 = О.

6.                   Решите уравнение:

        а) х^з - 7х + 6 = о;                  б) х^з - 43х + 42 = О;

Указа н и е. а) Представьте средний член трехчлена в виде суммы слагаемых —х и —6х.

2 Ашебра, 9 кл.

7.    Решите уравнение:

а) (х + 1) (х + 2) (х + 3) (х + 4) = 360; 6) (х - 1) (х - 3) (х - 5) (х - 7) - 105.

У ка з а н и е. а) Замените трехчленами произведение крайних множителей и произведение средних множителей.

8.    При каких значениях а не имеет корней уравнение:

          а) х⁴ — 6х² + а = О;                   6) х⁴ + ах² + 9 = 0?

С—15. Дробные рациональные уравнения

1.   При каких значениях с равно нулю значение дроби:

                 2с ^з — 8с                     с 4 —6с3 + 9с2

а)6) с ⁴ —81

2.   Решите уравнение

4а ³ + 8а ² — За —6

З. Найдите корни уравнения:

4.       Решите уравнение, обозначив одну из взаимно обратных дробей через t, а другую — через

5.       Решите уравнение, используя введение новой переменной:

5х х    х ² + 6

6.       Не выполняя построения, найдите координаты точек пересечения графиков функций у = х² + х — 4 и у — х

7.       Найдите корни уравнения

8.       Сумма некоторого положительного числа и числа, ему обратного, в 1,7 раза меньше суммы их квадратов. Найдите эти числа.

С--16. Решение неравенств второй степени с одной переменной

1.   Для каждой из парабол у = 2х2 — х — 15 и у = —3х2 +

а) определите направление ее ветвей;

б) найдите координаты точек пересечения параболы с осью х;

в) изобразите схематически график;

г) найдите по графику множество значений аргумента, при которых у < О и при которых у > О.

2.   Решите неравенство:

          а) х² — 8х + 15 > О;                    б) 3х² + 11х — 4 < О;

З. Найдите множество решений неравенства:

                        б) х² > 5;               в) 2х² > х;           г) —3х < 6х² .

4. Докажите, что при любом значении а верно неравенство:

      а) 5а ² — 2а + 1 > О;            б) ба < а ² + 10.

5. Найдите область определения функции:

6. При каких значениях с множеством решений неравенства х² — 6х + с < О является промежуток:

б) (—оо; +00)?

7. Решите неравенство х ² - 12х +35

С—17. Решение неравенств методом интервалов

1.   Решите неравенство:

   В) (Х + 9) (Х + 1) (Х — 11) > О;   г)                + 8) (х - 17) о;

(х + 3) (х - 8) (х - 20) > о;

      6)           + 10) (х - 3) о;

г)

2.   Найдите множество решений неравенства:

в) -(х - 1) (5 - х) (х + 20) > о;

2) а) (4х + 9) (10 - х) > О;                  6) (4 - х ² ) (10х + 35) < о;

в) (4х² - 9) (25 - х² ) (3х ² + 2) > о.

З. Решите неравенство:

4. Найдите область определения функции:

5. Решите неравенство:
а) (х +           -        - 18) > О;	х 2 - 13х +30 6) В +7 х +10
в) ..r3 — 5х 2 + 6х О;	Х 4 — 10х 2 + 9 г)

4 Х 12

С--18. Решение систем неравенств с одной переменной

1.   Решите систему неравенств:

6 — 5х < 4х — 2,О,

а) 300,

             4 — 2х      + 7;

2.   Найдите целые решения системы неравенств:

2х ² -3х -5 о,

а)6)

-х ² +8х -12

З. При каких отрицательных значениях х верно неравенство 3х ² + 5х — 2 О?

4.    Найдите область определения выражения:

                                                             (х ² — 5х +         О,

5.    Решите систему неравенств

(х ² +3х -1) ² 100.

6.    При каких значениях р система неравенств

4х           27 +X,

имеет решения? р + 6х < 2 + 5х

С-—19. Уравнение с двумя переменными и его график

1.                       Является ли пара чисел (2; —1) решением уравнения:

а) 5х — 2у — 8 = О;

2.                       Найдите три каких-нибудь решения уравнения:

а) 2х + у = З; б) ху — х = 14. З. Постройте график уравнения:

4.                   Какая фигура является графиком уравнения:

В)

5.                   Напишите уравнение окружности с центром в точке (З; —1), зная, что она: а) касается оси у; б) проходит через точку (9; —7).

6.                   Найдите все целые решения уравнения:

а) ху = —5;

С--20. Графический способ решения систем уравнений

1.     С помощью графиков, изображенных на рисунке б, решите систему уравнений у = —0,5х ² + 8, ху = 6.

2.     Постройте график функции у = х² — 4. С помощью этого графика решите систему уравнений:

а)           6)         в)

З. Решите графически систему уравнений: ху = 8,

а)6)

х ² + у ² = 25,

в)

у — 2х = О;

х ² + у ² = 16,

г)

4.          Изобразив схематически графики, выясните, имеет ли решения система уравнений и если имеет, то сколько:

 б)

5.          Решите графически систему уравнений:

(х -1) ² + (у -2) ² = 25,

а)6)

У = 2х.

6.          При каких значениях К система уравнений

а) имеет одно решение; б) имеет два решения; в) не имеет решений?

С--21. Решение систем уравнений второй степени

1.                       Является ли пара чисел х = 6, у = —8 решением системы уравнений

2.                       Решите систему уравнений

и выполните проверку.

З. Решите систему уравнений: х=у -2,

б)    в) ху — у = 10;

х2 - у2 = 24,     б) х — 2у = 7; у ² — ху = 12, зу-х 10

(х -         -1) = 30,

6)

2х-у 10

х + Зу = 11,

2x+Y ² = 14;

х ² — ху + у ² = 14

х - зу = 10.

4.     Имеет ли решение система уравнений

3х +2у = 11,

5х - зу = 12, х ² + у ² — ху — у = 6?

5.     Решите систему уравнений: а) {х2 6)

—у2 = 9,    х ² - зу ² = 22, ху = 20;  х ² +     = 28;

в)

6.     Не выполняя построения, найдите координаты точек пересечения окружности х² + (у — = 5 и параболы

7.     Решите систему уравнений:

С—22. Решение задач с помощью систем уравнений второй степени

1.      Разность двух чисел равна 5, а их произведение равно 84. Найдите эти числа.

2.      Прямоугольный участок земли площадью 2080 м² обнесен изгородью, длина которой равна 184 м. Найдите длину и ширину участка.

З. Периметр прямоугольника равен 20 см, а сумма площадей квадратов, построенных на его сторонах, равна 104 см² . Найдите стороны прямоугольника.

4.      Произведение двух чисел на 29 больше их суммы. Если к первому числу прибавить удвоенное второе число, то получится 19. Найдите эти числа.

5.      Найдите двузначное число, которое в 8 раз больше суммы его цифр и на 58 больше их произведения.

6.      Из двух пунктов, расстояние между которыми равно 18 км, вышли одновременно навстречу друг другу две группы туристов и встретились через 2 ч. Определите, с какой скоростью шла каждая группа, если известно, что на прохождение всего пути одной из них потребовалось на 54 мин больше, чем другой.

7.      Один из двух подъемных кранов разной мощности может разгрузить баржу на З ч быстрее, чем другой. При совместной работе им потребовалось бы затратить на разгрузку баржи 6 ч 40 мин. Сколько времени требуется каждому крану, чтобы разгрузить баржу?

С--23. Неравенства с двумя переменными

1.    Является ли пара чисел (—3; 5) решением неравенства:

       а) -4х + 2у - 23 > О;        б) х ² — 4ху — у ² 45?

2.    Найдите два каких-нибудь решения неравенства:

          а) у > 5х — 8;                  б) х² + у ² 25.

З. Изобразите на координатной плоскости множество точек, задаваемое неравенством:

        в) у Э 1 — х ² ,

4.Какое множество точек задается неравенством:

а) —х² + 3х — у + 4 < О;

5.Задайте неравенством с двумя переменными множество точек координатной плоскости, расположенных:

а) выше параболы у = 2х ² + 3х — 1;

б) вне круга с центром в точке (О; 4) и радиусом, равным 5.

С--24. Системы неравенств с двумя переменными

1.                       Является ли решением системы неравенств

пара чисел: а) (—1; О);

2.                       Изобразите на координатной плоскости множество решений системы неравенств:

      а)                     6) у > х2 +1,         в) (х -1) ²           +2) ²

З. Какую фигуру задает на координатной плоскости система неравенств:

               б)

Найдите площадь каждой фигуры.

4. Задайте системой неравенств с двумя переменными:

а) треугольник, изображенный на рисунке 7;

б) кольцо, изображенное на рисунке 8.

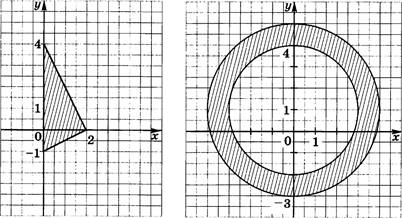
                 Рис. 7                                           Рис. 8

С—25. Последовательности

1.    Выпишите первые пять членов последовательности:

а) двузначных чисел, взятых в порядке возрастания;

б) квадратов натуральных чисел, взятых в порядке возрастания;

в) натуральных чисел, дающих при делении на З остаток 1, взятых в порядке возрастания.

2.    Последовательность (ап) задана формулой ап = 5n — 2.

Найдите: а) Щ; б) 06', в) аш; г) ашо•, д) ак•, е)

З. Найдите второй, пятый и десятый члены последовательности (хп), заданной формулой:

2п—1

                     з                   в) х п = п ² ,

е) хп = (—1) ^п • п.

4.       Последовательность задана формулой ап = 55 — 4n. Найдите номер члена последовательности, равного 15.

5.       Выпишите первые пять членов последовательности (сп), если:

= 24.

6.       Выпишите первые пять членов последовательности з

десятичных приближений с недостатком числа  взятых с точностью до 0,1; 0,01; 0,001 и т. д.

7.       Последовательность (а п) задана формулой ап = п ² —

— 2n + З. Является ли членом последовательности число: 6) 66; в) 103?

8.       Задайте формулой п-го члена последовательность (Щ), если:

= 5bn.

С--26. Арифметическая прогрессия. Формула п-го члена

1.           Зная первые два члена арифметической прогрессии 3,4; -0,2, найдите следующие за ними четыре ее члена.

2.           В арифметической прогрессии (bn) известны Ь -0,8 и d = 4. Найдите:

        а)                                           в) b24',                Г) bk+l

З. Найдите разность арифметической прогрессии (оп), если:

      а)        = 16, а = 37;                -11;

          в),           = -2,3.

4.      Мастерская изготовила в январе 106 изделий, а в каждый следующий месяц изготовляла на 12 изделий больше, чем в предыдущий. Сколько изделий изготовила мастерская в июне? в декабре?

5.      В арифметической прогрессии (хп) известны = 14 и d = 0,5. Найдите номер члена прогрессии, равного:

      а) 17,5;         б) 19;         в) 34.

6.      Выписали двадцать членов арифметической прогрессии:

18; 4,

Встретится ли среди них (и если да, то на каком месте) число:

     а) -38;     б) —64;    в) -80?

7.      Между числами 2 и 22 вставьте четыре числа так, чтобы вместе с данными числами они составили арифметическую прогрессию.

8.      Докажите, что если последовательность (ал) является арифметической прогрессией, то + а

9.      Первый член арифметической прогрессии равен 7. Найдите второй и третий ее члены, если известно, что они являются квадратами двух последовательных натуральных чисел.

10.  Докажите, что если числа 0² , b² и с ² составляют

                                                           1      1

арифметическую прогрессию, то числа и также составляют арифметическую прогрессию.

С—27. Формула суммы первых п членов арифметической прогрессии

1.     Последовательность —16; —13' является арифметической прогрессией. Найдите сумму первых п ее членов, если п равно:

               б) 16;                  в) 25;

2.     Найдите сумму первых двенадцати членов арифметической прогрессии, в которой:

в) а1 = 16,5, d =—1,5;

З. Найдите сумму первых пяти, сорока, К членов последовательности (оп), заданной формулой ап = Зп + 2.

4.      Найдите сумму:

а) всех натуральных чисел, не превышающих 80;

б) всех двузначных чисел;

в) всех четных чисел, не превышающих 100.

5.      Найдите сумму первых десяти членов арифметической прогрессии (ал), если:

б) а 4 = 16, а — 88.

6.      Тело в первую секунду прошло 15 м, а в каждую следующую проходило на 2 м больше, чем в предыдущую. Какой путь прошло тело за 26 с?

7.      Найдите первый член и разность арифметической прогрессии, в которой S3 = 48, ,.S6 = 141.

8.      Из пункта А выехал грузовой автомобиль и двигался со скоростью 40 км/ч. Одновременно в этом же направлении из пункта В отправился легковой автомобиль, который в первый час прошел 50 км, а в каждый следующий проходил на 5 км больше, чем в предыдущий. Через сколько часов легковой автомобиль догонит грузовой, если известно, что расстояние от пункта В до пункта А равно 135 км?

9.      Решите уравнение, в котором слагаемые в сумме, записанной в левой части, составляют арифметическую прогрессию:

а) 3 + 7 + 11 + + х = 253;

б) + 5 + 2 + + Х = —130.

Указан и е. Найдите сначала номер последнего члена прогрессии.

10.  Является ли арифметической прогрессией последовательность, сумма членов которой может быть найдена по формуле:

      а) sп = 5n ² + Зп;        6)     = ЗП ² •,        в) sп = (4n — 1) п?

С--28. Геометрическая прогрессия.

Формула п-го члена

1.     Зная первые два члена геометрической прогрессии 0,3; 1,8• найдите следующие за ними четыре члена.

2.     В геометрической прогрессии (ьп) известны = 1,6 и q = 2. Найдите:

З. Последовательность (ап) — геометрическая прогрессия. Найдите:  если а —  если а 1 —- 125,1

5'

В) ар если а1 —4

1  если а 1 -20,—

4.      Найдите первый член геометрической прогрессии (Щ), в которой:

               1       1

      а) b6 = 27                         б) Ь? = 256, q = —2.

5.      Найдите знаменатель геометрической прогрессии, если:

           а) Ь 12, = 48;                  6) = 25, = 16.

6.      Между числами        и 27 вставьте четыре числа так,

чтобы они вместе с данными числами составили геометрическую прогрессию.

7.      Последовательность (ал) — геометрическая прогрессия. Является ли геометрической прогрессией последовательность:

8.      Определите первый член и знаменатель геометрической прогрессии, если известно, что разность между ее четвертым и вторым членами равна 18, а разность между пятым и третьим членами равна 36.

9.      Даны четыре первых члена геометрической прогрессии. Сумма двух крайних членов равна 52, а двух средних равна 16. Найдите эти члены.

10.  Докажите, что если числа а, Ь, с составляют геометрическую прогрессию, то равенство

является тождеством.

С--29. Формула суммы первых п членов геометрической прогрессии

1.      Найдите сумму первых пяти членов геометрической прогрессии (ьп), в которой:

1

а)                          б) b1 = 27, 4'

     в)                20, q=J5.

2.      Найдите сумму первых шести членов геометрической прогрессии:

З. Последовательность (ап) — геометрическая прогрессия. Найдите:

1 а) S5, если а1 — 64 q 7'

1

б) * , если а1 - — 10,

2'

в) S4, если а —

     г) S6, если а 1 —         q= J72.

4.      Найдите сумму первых четырех членов геометрической прогрессии (ь п), в которой:

               1          1

              З 25'           125'           6) = 6, = 24,            О.

5.      Найдите первый член геометрической прогрессии,

2

в которой: а) q = 2, S5 = 93; б) q = 3'             = 65.

6.      Является ли геометрической прогрессией последовательность (х п), если:

                        б) хп = 2 ^п ;

При положительном ответе найдите сумму первых пяти ее членов.

7.      Разность между шестым и четвертым членами геометрической прогрессии равна 72, а между третьим и пятым равна 9. Найдите сумму первых восьми членов этой прогрессии.

8.      Сумма первых трех членов геометрической прогрессии равна 13, а сумма их квадратов равна 91. Найдите первый член прогрессии, ее знаменатель и сумму первых пяти членов.

Д С—ЗО. Комбинаторное правило умножения. Перестановки

1.     Укажите все способы, какими можно расставить пять книг на двух полках (учтите при этом случаи, когда одна из полок окажется пустой).

2.     Сколькими способами 9 участников конкурса могут выступить в порядке очередности в четверти финала конкурса?

З. Найдите значение выражения:

      а) 24! '       6)                в) 35! •

4.      Делится ли число 40! на: а) 410; 6) 500; в) 780?

зо

5.      Используя цифры О, З, 7, 8, составьте все возможные двузначные числа, в которых цифры не повторяются.

6.      Что больше и во сколько раз:

      а) 8! • 9 или 9! • 8;        б) (п — 1)! • п или п! • (п — 1)?

7.      На встрече выпускников 9 бывших одноклассников обменялись визитками. Сколько было использовано визиток?

8.      Сколько существует перестановок букв слова «фигура», в которых буквы «у», «р», «а» стоят рядом в указанном порядке?

С--31. Различные комбинаторные задачи

1.   Найдите значение выражения: 13!

      а)                    6)                   в)

2.   Сколькими способами можно выбрать на роли Винни-Пуха, Пятачка, Ослика Иа и Совы четырех из двенадцати актеров детского театра?

З. В Городской думе 10 депутатов моложе 30 лет. Сколькими способами можно выбрать из них троих для работы в комитете по молодежной политике?

4.      В районе л^т каждые два поселка соединены дорогой. Определите число таких дорог, если в районе 10 поселков.

5.      Сколько существует пятизначных телефонных номеров, начинающихся с цифры З, в которых все цифры различные?

6.      В пенале 12 ячеек для фломастеров. Сколькими способами можно разместить в пенале:

а) 8 различных фломастеров;

б) 12 различных фломастеров?

7.      Сколько среди всех перестановок букв слова «призма» таких, которые:

а) оканчиваются буквой «а»;

б) начинаются с буквы «р», а оканчиваются буквой «м»?

С-—32. Вероятность случайного события

1.     Из пенала, в котором лежат 8 простых и 12 цветных карандашей, достают один карандаш. Какова вероятность того, что этот карандаш окажется: а) простым;

б) цветным?

2.     Ученик задумал двузначное число. Какова вероятность того, что это число кратно З?

З. Какова вероятность того, что при бросании игрального кубика выпадет: а) З очка; б) менее 5 очков?

4.      На столе лежат пронумерованные экзаменационные билеты по геометрии. Рассматриваются следующие события: А — ученик достал билет с четным номером;

В — ученик достал билет с нечетным номером; С — ученик достал пронумерованный билет; D — ученик достал билет без номера.

Вероятность какого из этих событий равна О? равна 1? больше О, но меньше 1?

5.      В коробке 20 деталей, З из которых нестандартные. Наугад берут 5 деталей. Какова вероятность того, что все детали окажутся стандартными?

6.      Какова вероятность того, что при бросании двух кубиков сумма выпавших на них очков: а) равна 5; б) более 4?

7.      В круг радиуса 6 см вписан квадрат. Какова вероятность того, что выбранная наугад точка круга принадлежит квадрату? Ответьте на вопрос, учитывая, что л З.

Вариант ll

С—1а Функция. Задание функции формулой

1. Найдите:

1)    f(3), f(O), f(—2), если f(x) = 21х — 7;

2)    g(8), g(—3), g(O), если g(x) = х² — 10х;

З)               9(6), 9(0), если «х) =

2. Найдите значение х, при котором функция, заданная формулой

1)    f(x) = 12 — 5х, принимает значение, равное: а) 2; б) 24;

2)    g(x) = — х +9, принимает значение, равное: а) 10; б) 1;

З. Существует ли значение х, при котором значение функции, заданной формулой g (х) = — равно: а) 1;

б) —1,5; в) О? В случае утвердительного ответа укажите это значение.

4.    Зная, что х2 + 5

      а)                      , найдите f(5) + [ (—5);

6х2

4х3 _ Х

б) g(x) = , найдите g(2) + g(—2).

9

5.    Известно, что g(x) = Кх + Ь, причем g(1) = 5 и = —1 Найдите коэффициенты К и Ь.

С-—2. Область определения и область значений функции

1.    Найдите область определения функции, заданной

формулой:

53 1) а) f(x) = 37 — 3х;        б)

х

42 2) а) g(x) = 10 — х ² ;          б)

                             12

З Алгебра, 9 кл.

2.    Укажите область значений функции:

22

а) у = —24х + 5;    б) у = 41;        х

З. Найдите область значений функции:

        а) g(x) = 4х — 1, где 2             8;

б) h (х) = 5 — бх, где —3 х 4.

4.      Задайте формулой какую-либо функцию, областью определения которой является:

а) множество всех чисел, кроме 1 и 4;

б) множество всех чисел, больших или равных 6.

5.      Укажите область определения функции, заданной формулой:

С—3. График функции

1. На рисунке 9 изображен график функции у = g (х), областью определения которой служит промежуток [—3; 4]. Найдите:

б) g(O);                       в) g(1);

				2
				О х:

2) значения аргумента х, при которых: а) g(x) = З; б) g(x) = О;

в) g(x) —

З) наибольшее и наименьшее значения функции;

4) область значений функции.

2. Постройте график функЦИИ:

1) а) у = 0,5х + З;

- -0,5х - 2;

                                                               6                         8

х      х Рис. 9            х

З) а) у = х ² ,                      Ох;        в) у = ' х 1.

З. На рисунке 10 изображен график движения туристов от станции до озера. Пользуясь графиком, ответьте на вопросы:

                     Рис. 10                                      Рис. 11

1)    Сколько привалов делали туристы в пути, и какова продолжительность каждого привала?

2)    Сколько километров прошли туристы до первого привала? между первым и вторым привалами? после второго привала?

З) С какой скоростью шли туристы на каждом участке пути? 4) Через сколько часов туристы прибыли на озеро?

5) На каком расстоянии от озера находились туристы через 2 ч? через З ч? через 4 ч?

4. На рисунке 11 изображены графики движения пешехода (1) и велосипедиста (П), отправившихся из деревни на станцию, находящуюся от нее на расстоянии 32,5 км.

Пользуясь графиком, ответьте на вопросы:

1)    Кто выехал из деревни позже и на сколько?

2)    Сколько времени находился в пути пешеход? велосипедист?

З) Чему равна скорость движения пешехода? велосипедиста?

4)    Кто прибыл на станцию раньше и на сколько?

5)    Через сколько часов после своего выезда велосипедист догнал пешехода?

6)    Сколько километров оставалось идти пешеходу до станции в тот момент, когда велосипедист доехал до нее?

5.  Постройте график функции, предварительно заполнив таблицу:

х

10

где —6 х О;

х , где 1 х 6.

6.  Постройте график функции:

х + З, если х < —2, 1, если —2 х 2,

—х + З, если х > 2;

7.  Задайте с помощью нескольких формул функцию, график которой изображен на рисунке 12.

8.  Постройте график функх ^з + 3х ² — х — З ции g(x) =

                Рис. 12                                             2х ² - 2

С-—4. Свойства функций

1.                       Область определения функции, заданной графиком на рисунке 13, — промежуток [—3; 4]. Используя график, перечислите свойства функции. Найдите:

1)    а) нули функции; б) промежутки, в которых функция при нимает положительные значения, и промежутки, в которых функция принимает отрицательные значения;

2)    промежутки, в которых функция возрастает и в которых она убывает;

З) значение аргумента х, при котором функция принимает наибольшее значение и при котором она принимает наи-

меньшее значение;

4) область значений функции. Рис. 13

2.                       Выясните свойства функции:

у = 25х - 18;                б) у = -0,83х + 16,2;

в) У = -27; 36       63

                  х                    

З. Найдите нули функции (если они существуют):

1

1) а) у = -х-8;         = -0 4х + 32;

5 у = 9х (х — 5);       6)         16 (х ² + 2);

4.Постройте график функции g (х) = х — х и опишите ее свойства.

5.Выясните свойства функции

, если х < —2, f(x) = —2х, если —2 х 2,

, если х > 2.

С--5. Квадратный трехчлен и его корни

1.                       Найдите корни квадратного трехчлена: х² - 8х + 15;

в) 4b2 - 16b + 12;     5у 2 + 14у - З; в) -0,48 + 0,8;    0,5х 2 — х — 1;

г) 2а 2 — а; 6) 10b2 - 76 + 1; г) 7х2 - 28; б) -1008 + 20с + З;

в) —25а ² + 10а — 1.

2.                       Выделите квадрат двучлена из квадратного трех-

члена:

1) а) х² + 4х + 1;             6) ЗЬ² - 12b + 11;         в) у² + 2у;

З. Докажите, что при любом х квадратный трехчлен:

а) .r² — 10х + 28 принимает положительные значения;

б) —х² + 4х — 6 принимает отрицательные значения.

4. При каком значении Ь квадратный трехчлен:

а) b ² — 46 + 9 принимает наименьшее значение;

б) —b² + 66 — 14 принимает наибольшее значение?

5. Имеется прямоугольник со сторонами 8 и 12 см. Большую его сторону уменьшили на Ь см, а меньшую увеличили на столько же. При каком значении Ь площадь полученного прямоугольника окажется наибольшей?

С—б. Разложение квадратного трехчлена на множители

1.                        Разложите на множители квадратный трехчлен:

         б) 3х ² + 3х — 6;

в) 7х 2 - 63; 2) а) + х - 72; в) 12х 2 - 588;

г) 5х 2 + 19х — 4; 6) 7х2 + 20х - з; г) 3х2 - 12х + з.

2.                        Почему нельзя представить квадратный трехчлен в виде произведения многочленов первой степени:

 6) -3х² + 2х - 1; 2) а) х² - 12х + 39; 6) -4х² + 4х - з;

З. Сократите дробь:

4b + 1216-2х

б)в)           ² 62 _ 9             тс +21  8+7х— х а ² — 16а +63           уз + 7у2 - боу  з + 14b - 58

в) а ² - 81       10у - 50

4. Найдите значение дроби: х ² - 8х-33

1)                                            при х —- -9; 12; 111;

10х +30

8у — 56

2)                                             при х = -4; 22,5; 24.

У2 - 27у+ 14О

5.    Упростите выражение

9b- 4

6.    Постройте график функции

- 2х ² - 9х+ 18

18-2х2

Ш С--7. Функция у= ах² , ее график и свойства

1

1.   Зная, что g(x) = —х ² , заполните таблицу. 10

вааааааа

Постройте график функции g. Найдите: g(—3); g(3); g(—5); g(5).

В той же системе координат постройте график функ-

1                       ции f(x) = — х ² . Найдите: f(—3); f(3); f(—5); f(5).

10

2.   Не выполняя построения, найдите координаты точек пересечения графика функции у = —2х² и прямой:

      а) у = -200;          6) у = -3200;

       в) у = 40х;             г) у = -1400х.

З. Принадлежит ли графику функции у = 40х² точка:

а) А (-2; -160); 6) В (2; 160); в) С (0,1; 0,4)?

4.                        Постройте график функции

—х ² , если х > 1, g(x) =—х, если —1 х 1, х ² , если х < —1.

5.                        Какова область значений функции (укажите ее наибольшее и наименьшее значения):

а) у = 7х ² , где х е [—4; 8];

1                       б) у = ——х ² , где х е [—6; З]? з

6. Тело, падающее на землю, пролетает за t с расстояgt2 ние, равное s м, где s = g 10 м/с ² . Через какое вре2 мя тело достигнет земли, если в данный момент оно находится на высоте 560 м?

С--8, Графики функций у = ах² + п и у= а (х— ту

1.      Используя шаблон параболы у = х² , постройте график функции:

          а) у = .r² — 5;                          б) у = —х² + З;                    в) у = (х + 2) ² ;

2.      В каких координатных четвертях расположен график функции:

       а) у = 3х² - 2;           6) у : -2х ² - 4;          в) у = 5 (х — 8)² ?

З. Изобразите схематически график функции:

1 а)          = —4х ² — 1;        

2

в) у = —(х — 2)2 + З.

4. Найдите нули функции (если они существуют):

а) у = —9х2 + 1;                      5. Постройте график функции: а) y = lxl +1; б) y = lx — Щ; г)

в) у = —2х 2 -4- 16. в) у = Сх -з;

6. Постройте график функции:

С--9. Построение графика квадратичной функции

1.                        Найдите координаты вершины параболы:

       а) g(x) = х² + 4х + 2;         б) g(x) = —х ² — 6х + З;

в) g(x) = 4х ² — 8х — 1.

       При вычислении воспользуйтесь формулами т =           и

где т и п — координаты вершины параболы

g(x) = ах ² + bx + с.

2.                        Используя результаты вычислений в задании 1 а, постройте график функции g (х) = х² + 4х + 2. Найдите по графику:

а) нули функции; промежутки, в которых g(x) < О и g(x) > О;

б) промежутки убывания и возрастания функции; наименьшее ее значение.

З. Используя результаты вычислений в задании 16, постройте график функции g(x) = —х² — 6х + З. Найдите по графику:

а) нули функции; промежутки, в которых g(x) > О и

б) промежутки возрастания и убывания функции; наибольшее ее значение.

4.      Найдите область значений функции у = —х² + 4х + З, где х е [О; 5].

5.      При каких значениях Ь и с точка К (7; 2) является вершиной параболы у = х² + bx + с?

6.      Из лука выпущена стрела вертикально вверх с начальной скоростью 50 м/с. Зависимость расстояния s (м) от стрелы до земли от времени полета t (с) выражается формулой s = 50t — 5t ² . Постройте график этой зависимости. Найдите по графику:

1)    какой наибольшей высоты достигла стрела;

2)    в какой промежуток времени она поднималась вверх и в какой опускалась вниз;

З) через сколько секунд после пуска стрела упала на землю.

С-—10. Функция

1.    Зная, что g(x) = х⁸⁰ , сравните:

(1,423) и (1,327);         6) «-80,3) и «-78,2);

    в) «-23,1) и (18,7);         г) «-42,8) и (42,8);

и g(O,85); 3 ).

2.    Зная, что f(x) = х⁹⁵ , сравните: и [(21,8);      и [(52,3)•,        г) [(-47,2) и [(45,8);

б) f(—O,4) и f

З. Сколько корней имеет уравнение х^п = 450:

а) при четном п; б) при нечетном п?

4.

а)

27

125'

5.    Постройте график функции:

г) У = (х + 3)3.

6.    Сколько корней имеет уравнение:

       а) х^з = 23х + 7;          6) .х^з = 0,25х - 4;

       в) х⁴ = 23х + 7;        г) х ⁴ = 0,25х — 4?

7.    Принадлежит ли графику функции:

- х? точка М (-3,7; 549,827); точка К (-0,89; -12,749); = х^б точка Р (1,3; 1,0487); точка Q (-0,8; 1,8724)?

С--11. Корень п-й степени

1. Найдите значение выражения:

0,25;                   6) ^з 343;          в) ⁴ 0,0016;       

5 ³ 0,216;             б) 0,304; в) 63          8   г) 12 ⁴ 7—5881 •

З. Укажите два последовательных целых числа, между которыми заключено число:

      а)                  б)                       в) ⁴ 0,6;

4. Вычислите:

б)

д) (- ⁷0 ⁷ ;

б)

д)

5.

1

в) —х6 -2=о

32

6.                  При каких значениях переменной имеет смысл выражение:

а) ⁸ х+8; 6) ⁷ у -2;

7.                  Решите уравнение:

      а) х⁸ — 15х⁴ — 16 = О;           6) х⁴ - 10х² + 27 = о;

в) х⁶ — 7х³ — 8 = О.

8.                  Постройте график функции:

           а) у = Е; б) у = — 2.5;                   в) у = ф; г) у

С--12. Целое уравнение и его корни

1.    Определите степень уравнения:

а) х⁴ - х^з + 2х⁵ - 2 = О;

в) (х² + 6) (х — 5) — х(х + 1) (х — 1) = О;

          г) (5х⁴ - 1) (5х² - 2) - (5х³ +           = о.

2.    Какие из чисел —3; —2; —1; О; 1; 2; З являются кор-

нями уравнения:

      а) х^з — 9х = О;                      6) в (х - 7) + 7(х² - х) = -6;

в) х⁴ - 13х² + 36 = 0?

З. Решите уравнение:

5       2          6          з 2) а) (2х - 3) (х + 1) = + 17;

         б) (х - 7) (х + 7) + (х -            = 11х + зо -

х ² — 6х—4 11х в)г)

            27     з        з                            з             10

4.    Составьте какое-либо уравнение:

а) первой степени, корнем которого является число -11;

б) второй степени, имеющее корни 2 и —9;

в) третьей степени, имеющее корни 4; 7 и —7.

5.    х(2-х)

а)

                     2                     2                 2              з

                     9               18                 36

6.    Верно ли утверждение:

а) уравнение х⁶ + 3х⁴ + х² = —16 не имеет корней;

б) уравнение 25х (х + 2) — (5х — 1) (5х + 1) = 25 (2х — 1) + 26 не имеет корней;

в) уравнение 6х⁵ + 8х³ + 12х — 41 = О не имеет отрицательных корней;

г) уравнение 5х⁵ + 25х⁴ — 20х³ + 10х² — 5х = 17 не имеет целых корней?

С--13. Уравнения с параметрами

1. Найдите:

а) значение а, при котором корнем уравнения

является число 6;

б) значение с, при котором одним из корней уравнения 9х ² + + 2) - (3 - 2с) = о является число 5. Вычислите другой корень.

2. При каких целых значениях К корень уравнения Кх + 1 = 7 является целым числом?

З. При каких значениях Ь уравнение 4х — 2b = 5 имеет:

а) положительный корень;

б) отрицательный корень;

в) корень, больший 8;

г) корень, принадлежащий промежутку (1; З)?

4.      При каких значениях t имеет два корня уравнение:

       а) 2х² + 4х + t = О;             6) 6х² + + 6 = 0?

5.      При каких значениях с имеет один корень уравнение:

          а) 4х ² — 8х + с = О;               б) х² + сх + 16 = О?

6.      При каких значениях Ь не имеет корней уравнение:

7.      Найдите целые значения Ь, при которых корень уравнения Ь (2 — х) = 6 является отрицательным числом.

8.      Из данных уравнений выделите те, которые при любом значении а имеют два корня: х² + ах = О, х² + ах — 1 = О, х² + ах + 1 = О, х² — а = О.

9.      Найдите, при каких значениях п корнями уравнения 2х ² + пх — (18 — х) = О являются два противоположных числа.

10.  При каких значениях Ь уравнение х² - 4bx + 4b² - 1 = 0 имеет два различных корня, принадлежащие промежутку

С--14. Решение уравнений с помощью

разложения на множители и введения вспомогательной переменной

1. Решите уравнение:

1)     а) 18у^з - 36у² = О; б) х^з — 144х = О;

в) х² + 0,9х = о;

2)     а) 16х³ - 32х² - х + 2 = О,    б) х⁶ — х⁴ + 5х² — 5 = О;

в) у^б + 4у⁴ = у ² + 4.

2. Решите уравнение, используя введение новой переменной:

а) (х² - 10)² - з (х² - 10) + 4 = о;

б) (х² + ху — 5 (х² + х) + 6 = О;

в) (х ² + х + 6) (х² + х — 4) = 144.

З. Решите биквадратное уравнение:

        а) х⁴ - 10х ² + 9 = о;               6) х⁴ + 6х² - 27 = о;

        в) х⁴ - 18х ² + 32 = о;            г) х⁴ + 15х² + 54 = О;

            д) х⁴ - .х² - 12 = о;                         е) х⁴ + 25х² = О.

4.    Найдите координаты точек пересечения с осью абсцисс графика функции у = х⁴ — 3х² — 4.

5.    Решите уравнение х⁵ - х⁴ - 3х³ - 3х² - 4х - 4 = о.

6.    Решите уравнение:

       а) х^з - 13х + 12 = О;            6) х^з - 31х + зо = о;

в)  12 = о.

Указа н и е. а) Представьте средний член трехчлена в виде суммы слагаемых —х и —12х.

7.    Решите уравнение:

а) (х - 1) (х - 2) (х - 3) (х - 4) = 840; 6) (х + 1) (х + 3) (х + 5) (х + 7) = 945.

У ка за н и е. а) Замените трехчленами произведение крайних множителей и произведение средних множителей.

8.    При каких значениях а не имеет корней уравнение:

          а) х⁴ — 8х² + а = О;                 б) х⁴ + ах ² + 25 = О?

С—15. Дробные рациональные уравнения

1.    При каких значениях Ь равно нулю значение дроби: зы - 36 Ы + 10b ³ + 258

                   а)б)                                        9

Ы - 625

2.    Решите уравнение

х ³ + 6х ² — 5х —30 х ² — 36

З. Найдите корни уравнения:

             2          5             11

4.      Решите уравнение, обозначив одну из взаимно обратных дробей через t, а другую — через

5.      Решите уравнение, используя введение новой переменной:

6.      Не выполняя построения, найдите координаты точек пересечения графиков функций у = х ² + 2х — 9

18

х

7.      Найдите корни уравнения

8.      Сумма некоторого числа, большего 1, и числа, ему обратного, в 2— раза меньше разности их квадратов. Найдите эти числа.

С--16. Решение неравенств второй степени с одной переменной

1.                       Для каждой из парабол у = 3х² + х — 17 у = —2х2 _ - 5х + 12:

а) определите направление ее ветвей;

б) найдите координаты точек пересечения параболы с осью х;

в) изобразите схематически график;

г) найдите по графику множество значений аргумента, при которых у > О и при которых у < О.

2.                       Решите неравенство:

       а) - 10х + 21 > О;          б) 4х² + 11х          О;

         в) х ² — 16 > О;                             г) 5х — х² > О.

З. Найдите множество решений неравенства:

      а) х² < 9;                   в) 3х² х;          г) —4х < 8х² .

4. Докажите, что при любом значении Ь верно неравенство:

              а) 7b² - + 1 > О;                           6) 8b < + 17.

5. Найдите область определения функции:

    а)       х ² -18х+ 72;

7

•

6. При каких значениях с множеством решений неравенства .r² — 8х + с < О является промежуток:

б) (—оо; +00)?

7. Решите неравенство

х ² — 14х + 48

С--17. Решение неравенств методом

интервалов

1.   Решите неравенство:

 о;

2.   Найдите множество решений неравенства:

6) (6 - х) (3х + 12) о;

в) -(х - 2) (9 - х) (х + 10) > о;

6) (9 - х ² ) (6х + 30) < о;

в) (9х ² - 4) (16 - х² ) (2х ² + 3) > о.

З. Решите неравенство:

4. Найдите область определения функции:

(х + 34) (20 - х);(х - 7) (х +17) (х -19).

5.	Решите неравенство:
а)	(х + 13) (х -        (х - 15) > о;	б)	х 2 + 15х+56 - 12х+20
в)	хз - 10х2 + 21х о;	г)	х 4 - 17х 2 + 16

5х +20

С--18. Решение систем неравенств с одной переменной

1.    Решите систему неравенств:

2.    Найдите целые решения системы неравенств:

х ² — х — 2

а)6) 2х ² - 13х +15 о.

З. При каких отрицательных значениях х верно неравенство 4х² — 11х — З О?

4. Найдите область определения выражения:

С--19. Уравнение с двумя переменными и его график

1.                       Является ли пара чисел (—3; 1) решением уравнения:

а)

в)

2.                       Найдите три каких-нибудь решения уравнения:

      а) х — 4у = 5;              б) ху + х = 15.

З. Постройте график уравнения:

а)

4.                   Какая фигура является графиком уравнения:

5.                   Напишите уравнение окружности с центром в точке (—2; 1), зная, что она: а) касается оси х; б) проходит через точку (1; 5).

6.                   Найдите все целые решения уравнения:

а) ху = З;

С--20. Графический уравнений

1.   С помощью графиков, решите систему уравнений

способ решения систем

изображенных на рисунке 14,

ху = 6, у = 0,5х ² — 8.

2.   Постройте график функции у = —х² + 1. С помощью этого графика решите систему уравнений:

а)

б) в)

З. Решите       графически систему уравнений:

Рис. 14 а)б) У = 0,5х2, У -х=1;

              х ² + у ² = 16,                х2 + у2 = 36,

в)г)

4.     Изобразив схематически графики, выясните, имеет ли решения система уравнений и если имеет, то сколько:

5.     Решите графически систему уравнений:

                                                (х -2) ²          -3) ² = 16,

а)б)

6.     При каких значениях т система уравнений х2 +у2 = 9,

а) имеет одно решение; б) имеет два решения; в) не имеет решений?

С--21. Решение систем уравнений второй степени

1.    Является ли пара чисел х = 7, у = —6 решением сисХУ + 42 = О,

темы уравнений х ² — 2у —61 = О?

х ² — 5у — 24 = О,

2.    Решите систему уравнений

У=х-2 и выполните проверку.

З. Решите систему уравнений: ху + х2 = 4,

6)в)

ху х —2у = 7;

                                                       6)в)                          + у ² = 24,

х? + ху — у ² = 4, 6)

3х +у = 10.

4.                  Имеет ли решение система уравнений

5х + Зу = 14, 2х - 5у = 18, х ² + у ² + 2ху — х = О?

5.                  Решите систему уравнений:

2х ² — у ² = 41, а)6) 2х ² + у² = 59;

в)

6.                  Не выполняя построения, найдите координаты точек пересечения окружности х² + (у — = 13 и параболы у = х² — 10.

7.                  Решите систему уравнений:

           1   1    1

а) х у — 12'

2х — у = 2;

С—22. Решение задач с помощью систем уравнений второй степени

1.     Сумма двух чисел равна 25, а их произведение равно 144. Найдите эти числа.

2.     Прямоугольный участок земли площадью 3250 м² обнесен изгородью, длина которой равна 230 м. Найдите длину и ширину участка.

З. Периметр прямоугольника равен 24 см, а сумма площадей квадратов, построенных на его сторонах, равна 148 см ² . Найдите стороны прямоугольника.

4.      Произведение двух чисел на 13 больше их суммы. Если из первого числа вычесть утроенное второе число, то получится 9. Найдите эти числа.

5.      Найдите двузначное число, которое в 7 раз больше суммы его цифр и на 34 больше их произведения.

6.      Из пункта А в пункт В, расстояние между которыми 360 км, выехали одновременно два автомобиля. За З ч первый из них прошел расстояние на 30 км больше, чем второй. Найдите скорость каждого автомобиля, если известно, что на весь путь первый автомобиль затратил на полчаса меньше, чем второй.

7.      Два тракториста, работая совместно, могут вспахать поле за 2 ч 40 мин. Сколько времени потребуется каждому трактористу в отдельности для выполнения этой работы, если известно, что первый из них может выполнить ее на 4 ч быстрее второго?

С--23. Неравенства с двумя переменными

1.    Является ли пара чисел (З; —4) решением неравенства:

а) 5х - у - 18

2.    Найдите два каких-нибудь решения неравенства:

        а)                 б) у > 5 — х ² .

З. Изобразите на координатной плоскости множество точек, задаваемое неравенством:

4. Какое множество точек задается неравенством:

        а)             б) х² + + 6х - 8у - 11

5. Задайте неравенством с двумя переменными множество точек координатной плоскости, расположенных:

а) ниже параболы у = —х² + 4х+ 1;

б) вне круга с центром в точке (—6; О) и радиусом 4.

С-—24. Системы неравенств с двумя переменными

1.   Является ли решением системы неравенств х ² — у <О,

пара чисел: а) (—3; 4); б) (2; 5); в) (О; —2)?

2.   Изобразите на координатной плоскости множество решений системы неравенств:

      в)

З. Какую фигуру задает на координатной плоскости система неравенств:

              б)

Найдите площадь каждой фигуры.

4. Задайте системой неравенств с двумя переменными:

а) треугольник, изображенный на рисунке 15;

б) кольцо, изображенное на рисунке 16.

              Рис. 15                                          Рис. 16

ш С-—25. Последовательности

1.    Выпишите пять первых членов последовательности:

а) двузначных чисел, взятых в порядке убывания;

б) кубов натуральных чисел, взятых в порядке возрастания;

в) натуральных чисел, дающих при делении на 5 остаток 2, взятых в порядке возрастания.

2.    Последовательность (хп) задана формулой х п = бп — 1.

Найдите:

                                             В) Х2о•,                                         100; д) хк;

З. Найдите третий, шестой и двадцатый члены последовательности (ал), заданной формулой:

Зп— 1

2

е) ап = (—1) ^п .

4.      Последовательность задана формулой х п = 46 — Зп. Найдите номер члена последовательности, равного 25.

5.      Выпишите пять первых членов последовательности (с п), если:

 б) = 32, с           — 0,5с .

б. Выпишите первые пять членов последовательности

2

десятичных приближений с недостатком числа взятых с точностью до 0,1; 0,01; 0,001 и т. д.

7. Последовательность (Л) задана формулой ьп = п ²

— 4n + 9. Является ли членом последовательности число: 6) 59; в) 409?

При положительном ответе укажите номер члена.

8. Задайте формулой п-го члена последовательность (хп), если:

С--26. Арифметическая прогрессия.

Формула п-го члена

1.     Зная первые два члена арифметической прогрессии найдите следующие за ними четыре ее члена.

2.     В арифметической прогрессии (ап) известны а = -1,2 и d = З. Найдите:

                                           в) аи,

З. Найдите разность арифметической прогрессии (Оп), если:

а) а1 = 5, ав = 19; б) а1 = 2, аи = —5; 1 = -0,3, = 1,9.

4.       Бригада стеклодувов изготовила в январе 80 изделий, а в каждый следующий месяц изготовляла на 17 изделий больше, чем в предыдущий. Сколько изделий изготовила бригада в августе? в декабре?

5.       В арифметической прогрессии (bn) известны bl = 12 и d = З. Найдите номер члена прогрессии, равного:

6.       Выписали двадцать членов арифметической прогрессии: 6,5; 8'

Встретится ли среди них (и если да, то на каком месте) число: а) 13; б) 22,5; в) 36?

7.       Между числами 64 и 46 вставьте пять чисел так, чтобы они вместе с данными числами составили арифметическую прогрессию.

8.       Докажите, что если последовательность (хп) является арифметической прогрессией, то х4 + х п 4 = х6 + хп 6

9.       Первый член арифметической прогрессии равен 47. Найдите второй и третий ее члены, если известно, что они являются квадратами двух последовательных натуральных чисел.

                                                  1      1        1

10.   Докажите, что если числа  состав-

ляют арифметическую прогрессию, то числа 0² , 6² и с ² также составляют арифметическую прогрессию.

С--27. Формула суммы первых п членов арифметической прогрессии

1.     Последовательность 4; —6' является арифметической прогрессией. Найдите сумму первых п ее членов, если п равно: а) 8; б) 18; в) 35;

2.     Найдите сумму первых десяти членов арифметической прогрессии, в которой:

а)

                   в) -2,5;                            г) = 2-0, d=Ji.

З. Найдите сумму первых шести, двадцати, К членов последовательности (ха), заданной формулой хп = 4n + 5.

4.       Найдите сумму:

а) всех натуральных чисел, не превышающих 50;

б) всех натуральных чисел, кратных 4, не превышающих 100;

в) всех нечетных чисел, не превышающих 100.

5.       Найдите сумму первых двенадцати членов арифметической прогрессии (ап), если:

б) аб = 12, щ 6 - 100.

6.       Тело в первую секунду прошло 12 м, а в каждую следующую проходило на З м больше, чем в предыдущую. Какой путь прошло тело за полчаса?

7.       Найдите первый член и разность арифметической прогрессии, в которой S3 = 60, S7 = 56.

8.       Из пунктов А и В, расстояние между которыми равно 450 км, выехали одновременно навстречу друг другу два автомобиля. Один автомобиль двигался равномерно со скоростью 60 км/ч, а другой в первый час прошел 45 км, а в каждый следующий проходил на 5 км больше, чем в предыдущий. Через сколько часов автомобили встретились?

9.       Решите уравнение, в котором слагаемые в сумме, записанной в левой части, составляют арифметическую прогрессию:

а) 2 + 6 + 10 + + х = 450; 6) ЗО + 27 + 24 + + х = 162.

Указание. Найдите сначала номер последнего члена прогрессии .

10.   Является ли арифметической прогрессией последовательность, сумма членов которой может быть найдена по формуле:

в) s п = 4n ² ?

С--28. Геометрическая прогрессия.

Формула п-го члена

1.      Зная первые два члена геометрической прогрессии 1,6; 0,8, найдите следующие за ними четыре члена.

2.      В геометрической прогрессии (а п) известны = 3,2

1

Найдите:

З. Последовательность сия. Найдите:

а) b6, если b1 = 2, q = З;

1

      в) Щ, если b1 = 128,        4'

4.       Найдите первый член

1

— геометрическая прогрес-

б) Л, если = 16 q

г) Ьт, если b1 = 4, q = О.

геометрической прогрессии

1

(оп), в которой: а) а5 —          ч- 2'           6)          = 243, ч = -3.

64'

5.       Найдите знаменатель геометрической прогрессии (Щ), в которой: а) Ь 5 - 11, — ь— - 100, b8 = 9.

1

6.       Между числами — и 16 вставьте три числа так, что16

бы они вместе с данными числами составили геометрическую прогрессию.

7.       Последовательность (ап) — геометрическая прогрессия. Является ли геометрической прогрессией последова-

тельность:

            а) at — 1; — 1; аз — 1 •                          б) 4q; 402', 4а •

            1    1    1

в)

щ ' а2 аз

8.       Определите первый член и знаменатель геометрической прогрессии, если известно, что разность между ее пятым и третьим членами равна 72, а разность между четвертым и вторым членами равна 36.

9.       Даны первые четыре члена геометрической прогрессии. Сумма двух крайних членов равна 13, а двух средних равна 4. Найдите эти члены.

10.   Докажите, что если числа а, Ь, с и d составляют геометрическую прогрессию, то равенство

(а — = (а — су + (Ь — су + (Ь —

является тождеством.

С—29. Формула суммы первых п членов геометрической прогрессии

1.     Найдите сумму первых шести членов геометрической прогрессии (ь п), в которой:

1

- 27,

3'

16,

2

2.     Найдите сумму первых пяти членов геометрической прогрессии:

в) З;

З. Последовательность (ап) — геометрическая прогрессия. Найдите:

                                     1                                         1

        а) * , если а1 = 81, q= —3'          б) * , если = 18,          ——2'

в) S4, если а1 = 4, q —г) S8, если а 1 = ф, q=J5.

4.      Найдите сумму первых пяти членов геометрической прогрессии (Щ), в которой:

               1         1

                 5 — 64'                 6) = 4, = 36,            О.

16'

5.      Найдите первый член геометрической прогрессии, в которой:  = 65; 6) 2, = 765.

6.      Является ли геометрической прогрессией последовательность (bn), если:

а) bn = 43

При положительном ответе найдите сумму первых четырех ее членов.

7.      Разность между пятым и третьим членами геометрической прогрессии равна 144, а между четвертым и вторым равна 48. Найдите сумму первых шести членов этой прогрессии.

8.      Сумма первых трех членов геометрической прогрессии равна 14, а сумма их квадратов равна 84. Найдите первый член прогрессии, ее знаменатель и сумму первых шести членов.

С—ЗО. Комбинаторное правило умножения. Перестановки

1.     Укажите все способы, какими можно разложить четыре мяча в две корзины (учтите при этом случаи, когда одна из корзин окажется пустой).

2.     Курьер должен развезти пиццу по шести адресам. Сколько маршрутов он может выбрать?

З. Найдите значение выражения: 36 !

      а)                б)                в)

48! • 5!'

4.      Делится ли число 50! на: а) 400; б) 98; в) 510?

5.      Используя четные цифры О, 2, 4, 6, 8, составьте все возможные трехзначные числа, в которых цифры не повторяются.

6.      Что больше и во сколько раз:

      а) 10! • 8 или 8! • 10;            б) (п + 2)! • п или п! • (п + 2)?

7.      На конференции 7 ее участников обменялись номерами телефонов. Сколько было произведено обменов телефонными номерами?

8.      Сколько существует перестановок букв слова «вершина», в которых буквы «в», «е», «р» стоят рядом в указанном порядке?

С--31. Различные комбинаторные задачи

1.                       Найдите значение выражения:

31 •

      а)                             б)в)

2.                       Сколькими способами можно выбрать старосту, помощника старосты и ответственного за дежурство по школе из 32 учащихся класса?

З. В группе 9 студентов хорошо владеют иностранным языком. Сколькими способами можно выбрать из них четверых для работы на практике с иностранцами?

4.      На плоскости отмечены 9 точек, никакие три из которых не лежат на одной прямой. Сколько прямых можно провести через эти точки?

5.      Сколько существует шестизначных телефонных номеров, начинающихся на 36, в которых все цифры различные?

6.      На странице альбома 10 свободных мест для марок. Сколькими способами можно вложить в свободные места: а) 6 различных марок; б) 10 различных марок?

7.      Сколько среди всех перестановок букв слова «цифра», таких, которые:

а) начинаются с буквы «ц»;

б) начинаются с буквы «ф», а оканчиваются буквой «р»?

С--32. Вероятность случайного события

1.     Из коробки, в которой хранятся 5 черных и 7 белых шаров, достают один шар. Какова вероятность того, что этот шар окажется: а) черным; б) белым?

2.     Ученик задумал двузначное число. Какова вероятность того, что оно является квадратом некоторого числа?

З. Какова вероятность того, что при бросании игрального кубика выпадет: а) 2 очка; б) более З очков?

4. В холодильнике хранятся пакеты только с яблочным и апельсиновым соками. Рассматриваются следуюЩИе события:

А — достали пакет с яблочным соком;

В — достали пакет с апельсиновым соком;

С — достали пакет с соком;

D — достали пакет с вишневым соком.

Вероятность какого из этих событий равна О? равна 1? больше О, но меньше 1?

5.      В пачке 25 тетрадей, 5 из которых в линейку, а остальные в клетку. Наугад берут 7 тетрадей. Какова вероятность того, что все тетради окажутся в клетку?

6.      Какова вероятность того, что при бросании двух кубиков сумма выпавших на них очков: а) равна 4; б) менее З?

7.      В квадрат со стороной 6 см вписан круг. Какова вероятность того, что выбранная наугад точка квадрата принадлежит кругу? Ответьте на вопрос, учитывая, что

КОНТРОЛЬНЫЕ РАБОТЫ

1

•1. Дана функция f(x) = 17х — 51. При каких значениях аргумента f(x) = О, f(x) < О, f(x) > О? Является ли эта функция возрастающей или убывающей?

⁰ 2. Разложите на множители квадратный трехчлен:

а) х² — 14х + 45;         6) зу² + 7у - 6.

Зр ² + р— 2 ^о з. Сократите дробь

4—9р2

4.       Область определения функции g (рис. 17) — отрезок [—2; 6]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.

Рис. 17

5.       Сумма положительных чисел а и Ь равна 50. При каких значениях а и Ь их произведение будет наибольшим?

                   2                                                   

—13х + 65.

< О, g(x) или убывающей?

•2. Разложите на множители квадратный трехчлен:

а) х² — 10х + 21;       б) 5у ² + 9у — 2.

48 + 7с-2 ^о з. Сократите дробь

1—168

4.      Область определения функции f (рис. 18) — отрезок [—5; 4]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.

5.      Сумма положительных чисел с и d равна 70. При каких значениях с и d их произведение будет наибольшим?

                   З                                                  

      •1.                                       1,3х — 3,9.

< О, [ (х) или убывающей?

⁰ 2. Разложите на множители квадратный трехчлен:

а) х² - 12х + 35;            6) 7у² + 19у - 6.

5а ² + 19а—4 ^о з. Сократите дробь

1-2502

4.      Область определения функции f (рис. 19) — отрезок [—1; 6]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.

Рис. 19

5.      Сумма положительных чисел а и Ь равна 46. При каких значениях а и Ь их произведение будет наибольшим?

                         4                                                               

—1,2х + 4,8.

< О, g(x) или убывающей?

⁰ 2. Разложите на множители квадратный трехчлен:

а) х² — 18х + 45;                     6) 9у ² + 25у - 6.

76 ² +11b-6 ^о з. Сократите дробь

9— 49b2

4.      Область определения функции g (рис. 20) — отрезок [—3; 5]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.

5.      Сумма положительных чисел т и п равна 62. При каких значениях т и п их произведение будет наибольшим?

⁰ 1. Постройте график функции у = х² — 6х + 5. Найдите с помощью графика:

а) значение у при х = 0,5;

        б) значения х, при которых у        1

в) нули функции; промежутки, в которых у > О и в которых у < О;

г) промежуток, на котором функция возрастает.

⁰ 2. Найдите наименьшее значение функции

З. Найдите область значений функции у = х² — 6х — 13, где Х Е [—2; 7]•

4.Не выполняя построения, определите, пересекаются ли парабола у = —х ² и прямая у = 5х — 16. Если точки пересечения существуют, то найдите их координаты.

—3! +12 ⁴ 7—58•

5.Найдите значение выражения ^з

81

Вариант 2                                   

• 1. Постройте график функции у = х ² — 8х + 13. Найдите с помощью графика:

а) значение у при х = 1,5;

б) значения х, при которых у = 2;

в) нули функции; промежутки, в которых у > О и в которых у < О;

г) промежуток, в котором функция убывает.

•2. Найдите наибольшее значение функции у = —х² + 6х — 4.

З. Найдите область значений функции у = х² — 4х — 7, где х [—1; 5].

4.Не выполняя построения, определите, пересекаются ли парабола у = —х ² и прямая у = 20 — 3х. Если точки пересечения существуют, то найдите их координаты.

5.Найдите значение выражения ^з -2 ²² +8 4 5 1 •

                                                                        27            16

Постройте график функции у = х ² — 4х — 5. Найдите с помощью графика:

а) значение у при х = 0,5;

б) значения х, при которых у = З;

в) нули функции; промежутки, в которых у > О и в которых у < О;

г) промежуток, в котором функция возрастает.

⁰ 2. Найдите наименьшее значение функции у = + 2х - 24.

З. Найдите область значений функции у = х ² — 2х — 8, где х Е [—1; З].

4.                   Не выполняя построения, определите, пересекаются ли парабола у = —х ² и прямая у = 6х — 15. Если точки пез ресечения существуют, то найдите их координаты.

                                                                        17            13

5.                   Найдите значение выражения ^з        •

                                                                        27            81

Вариант 4                                          

⁰ 1. Постройте график функции у = х ² — 2х — 8. Найдите с помощью графика:

а) значение у при х = —1,5;

б) значения х, при которых у = З;

в) нули функции; промежутки, в которых у > О и в которых у < О;

г) промежуток, в котором функция возрастает.

      •2. Найдите         наибольшее        значение         функции

З. Найдите область значений функции у = х² — 2х — З, где х е [О; З].

4. Не выполняя построения, определите, пересекаются ли парабола у = —х ² и прямая у = 12 — х. Если точки пере2 сечения существуют, то найдите их координаты.

                                                                          19            1

5. Найдите значение выражения 2 ⁵ —7— + ⁴ 39 •

                                                                          32           16

уравнение:

а) х^з — 81х = О;

б)

5                     4

       ⁰ 2. Решите биквадратное уравнение          - 19х² + 48 = о.

аз — 202 _ 9а + 18

^о з. При каких а значение дроби  равно 02 — 4 нулю?

4. Решите уравнение:

       Зу +2    у-з       з

а)

4у ² + у 16у ² — 1 — 4у — 1'

6.                   (х² + 3х + 1) (х² + 3х - 9) = 171.

5. Найдите координаты точек пересечения графиков функций у = и у = х? — 3х + 1.

Вариант 2

•1. Решите уравнение:

а) х^з — 64х = О;

х ² — 4 6— х

6) з   2

•2. Решите биквадратное уравнение х⁴ — 20х² + 64 = О.

- 5b² - 4b +20

⁰ 3. При каких Ь значение дробиравно b2 — 25 нулю?

4. Решите уравнение:

             10у         у-5         у-з

а)

9у ² - 4 ЗИ+2 - 2-Зу'

6) (х² + 5х + 6) (х² + 5х + 4) = 840.

5. Найдите координаты точек пересечения графиков х        3х-4

функций у =

уравнение:

а) х ^з — 36х = О;

х ² — 1 х — 1

б)

6                     4

⁰ 2. Решите биквадратное уравнение х⁴ — 29х ² + 100 = О.

а ^з + 108-30 ² - Зба

^о з. При каких а значение дроби  рав-

а ² — 9

но нулю?

4. Решите уравнение:

           5у-6 з-зу        з

     а)                          

0 ² - 9 3+2у 2у-З'

6) (х² - х + 1) (х ² - х - 2) = 378.

5. Найдите координаты точек пересечения графиков функций у — и у = х² + 2х.

Вариант 4                                      

• 1. Решите уравнение:

а) х^з - 25х = О;

„- ² - 1 3х-1

6)

                   2               4

⁰ 2. Решите биквадратное уравнение х⁴ - 40х² + 144 = о.

⁰ 3. При каких с значение дроби  равно

с ² — 49

нулю?

4. Решите уравнение:

20у  2у-з 5-2у а)

Збу ² - 4 2-6у - бу +2'

6) (х² + 3х + 4) (х ² + 3х + 9) = 266.

5. Найдите координаты точек пересечения графиков

функций у — и у = х ² — 20. х + 20

      •1.                неравенство:

       а) 2х² - 7х                о;

в) 4х² — х + 1 > О.

•2. Решите неравенство, используя метод интервалов:

З. При каких значениях т уравнение 3х² + тх + + 12 —— О имеет два корня?

4.    Решите неравенство:

        5х+1                3х-1

а)

5.    Найдите область определения функции:

      в)           16—х2 + 7 — 5х.

Вариант 2

•1. Решите неравенство:

а) 3х² - 5х - 22 > О;

в) 2х² + 3х + 8 < о.

⁰ 2. Решите неравенство, используя метод интервалов:

З. При каких значениях п уравнение 5х ² + пх + 20 = О не имеет корней?

4.    Решите неравенство:

      а)             >О;         6)

5.    Найдите область определения функции:

              5х — 4х ² •                    

    в)        9-х ² + 5-2х.

неравенство:

      а) 2х ² - 13х + 6 < о;         б) х ² > 9;

в) 3х ² - 6х + 32 > о.

•2. Решите неравенство, используя метод интервалов:

З. При каких значениях р уравнение 2х ² + рх + 2 = О имеет два корня?

4.     Решите неравенство:

а)

5.     Найдите область определения функции:

3х+ 18

Вариант 4                                      

• 1. Решите неравенство:

      а) 5х² + 3х — 8 > О;           б) х ² < 16;

в) 5х² — 4х + 21 > О.

•2. Решите неравенство, используя метод интервалов: (х + 8) (х - 5) (х + 10) < о.

З. При каких значениях t уравнение 25х ² + tx + 1 = О не имеет корней?

4.     Решите неравенство:

2х-4

а)б)

5.     Найдите область определения функции:

⁰ систему уравнений х — 2у = 1, ху + у = 12.

•2. Одна из сторон прямоугольника на 7 см больше другой, а его диагональ равна 13 см. Найдите стороны прямоугольника.

З. Не выполняя построения, найдите координаты точек пересечения окружности х² + у² = 5 и прямой

4.Изобразите на координатной плоскости множество решений системы неравенств

5.

Решите систему уравнений х

Вариант 2                                                                К—5 (S 7, 8)

• 1. Решите систему уравнений

3х + у = 10,

⁰ 2. Периметр прямоугольника равен 14 см, а его диагональ равна 5 см. Найдите стороны прямоугольника.

З. Не выполняя построения, найдите координаты точек пересечения параболы у = х² — 14 и прямой х + у = 6.

4. Изобразите на координатной плоскости множество решений системы неравенств х ² + у ² <16,

5. Решите систему уравнений

систему уравнений 3х + у — х — ху = 8.

⁰ 2. Одна из сторон прямоугольника на 4 см больше другой. Найдите стороны прямоугольника, если его площадь равна 45 см ² .

З. Не выполняя построения, найдите координаты точек пересечения окружности .r² + у ² = 17 и прямой 5х - зу = 17.

4. Изобразите на координатной плоскости множество решений системы неравенств

5. Решите систему уравнений у

Вариант 4                                                                К—5 (S 7, 8)

• 1. Решите систему уравнений х — 5у = 2, х ² — у = 10.

⁰ 2. Периметр прямоугольника равен 26 см, а его площадь равна 42 см² . Найдите стороны прямоугольника.

З. Не выполняя построения, найдите координаты точек пересечения параболы у = х² — 8 и прямой х + у = 4.

4. Изобразите на координатной плоскости множество решений системы неравенств х ² + у ² 9,

5. Решите систему уравнений х

⁰ Найдите тридцатый арифметической прогрессии (а п), если = —25 и d = 4.

⁰ 2. Найдите сумму первых пятнадцати членов арифметической прогрессии (оп), если al = 2 и аск = 5.

^о з. Является ли число —6 членом арифметической прогрессии (сл), в которой ст = 30 и ст = 21?

4.       Найдите сумму первых двадцати членов последовательности, заданной формулой ь п = 2n + 1.

5.       Найдите сумму всех натуральных чисел, кратных 4 и не превышающих 150.

Вариант 2                                  К—6 (S 9)

• 1. Найдите сороковой член арифметической прогрессии (ал), если = 38 и d = —3.

•2. Найдите сумму первых двадцати членов арифметической прогрессии (ап), если а1 = 1 и а2 = 6.

^о з. Является ли число 39 членом арифметической прогрессии (сп), в которой = —6 и с9 = 6?

4.      Найдите сумму первых тридцати членов последовательности, заданной формулой ьп = Зв — 1.

5.      Найдите сумму всех натуральных чисел, кратных З и не превышающих 80.

Найдите двадцать третий арифметической прогрессии (ал), если = —15 и З.

•2. Найдите сумму первых шестнадцати членов арифметической прогрессии (ап), если ar = 8 и = 4.

^о з. Является ли число 5 членом арифметической прогрессии (сп), в которой = —31 и % — 11 ⁹

4.       Найдите сумму первых шестидесяти членов последовательности, заданной формулой bn = 4n — 2.

5.       Найдите сумму всех натуральных чисел, кратных 7 и не превышающих 150.

Вариант 4

• 1. Найдите сорок третий член арифметической прогрессии (оп), если а1 = —9 и d = 4.

⁰ 2. Найдите сумму первых четырнадцати членов арифметической прогрессии (ал), если а1 = —63 и а2 —- -58.

^о з. Является ли число 36 членом арифметической прогрессии (ьп), в которой bl = —16 и

4.       Найдите сумму первых ста двадцати членов послеДОВаТеЛЬНОСТИ, заданной формулой ап = Зп — 2.

5.       Найдите сумму всех натуральных чисел, кратных 9 и не превышающих 80.

(S 10)

Найдите седьмой геометрической прогрессии фа), если = 1500 и q = —0,1.

•2. Последовательность (bn) — геометрическая прогрессия, в которой Ь 4 = 18 и q = Ф. Найдите bl.

^о з. Найдите сумму первых шести членов геометрической прогрессии (Щ), в которой bl = 8 и q = —

4.       Известны два члена геометрической прогрессии: b4 = 2 и b6 = 200. Найдите ее первый член.

5.       Сумма первых четырех членов геометрической прогрессии равна 45, знаменатель прогрессии равен 2. Найдите сумму первых восьми членов этой прогрессии.

Вариант 2                                         (S 10)

• 1. Найдите восьмой член геометрической прогрессии (Щ), если b1 = 0,0027 и q = —10.

⁰ 2. Последовательность (bn) — геометрическая прогрессия, в которой b6 = 40 и q = а. Найдите 61.

^о з. Найдите сумму первых шести членов геометрической прогрессии (bn), в которой b1 = 81 и q = З.

4.      Известны два члена геометрической прогрессии: b5 = 0,5 и Ь? = 0,005. Найдите ее первый член.

5.      Сумма первых трех членов геометрической прогрессии равна 26, знаменатель прогрессии равен З. Найдите сумму первых шести членов этой прогрессии.

(S 10)

Найдите шестой член геометрической прогрессии (Щ), если b1 = 0,81 и — —. з

⁰ 2. Последовательность (Щ) — геометрическая прогрессия, в которой b5 = 432 и q= Мб. Найдите 61.

•З. Найдите сумму первых восьми членов геометрической прогрессии (Щ), в которой b1 = 16 и q = 2.

4.       Известны два члена геометрической прогрессии: = 4,8 и = 38,4. Найдите ее первый член.

5.       Сумма первых трех членов геометрической прогрессии равна —105, знаменатель прогрессии равен 4. Найдите сумму первых пяти членов этой прогрессии.

Вариант 4                                К—7 (S 10)

• 1. Найдите пятый член геометрической прогрессии (Щ), если b1 = —125 и q = 0,2.

•2. Последовательность (Ьп) — геометрическая прогрессия, в которой = 27 и q = ф. Найдите Щ.

⁰ 3. Найдите сумму первых девяти членов геометрической прогрессии (Щ), в которой = 0,08 и = 0,64.

4.       Известны два члена геометрической прогрессии:  = 14,4 и b6 = 388,8. Найдите ее первый член.

5.       Сумма первых трех членов геометрической прогрессии равна 28, знаменатель прогрессии равен —. Найдите сумму первых семи членов этой прогрессии.

(S 11, 12)

• Сколькими способами могут разместиться 5 человек в салоне автобуса на пяти свободных местах?

⁰ 2. Сколько трехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 1, 2, 5, 7, 9?

^о з. Победителю конкурса книголюбов разрешается выбрать две книги из 10 различных книг. Сколькими способами он может осуществить этот выбор?

•4. В ящике находятся шары с номерами 1, 2, З, 25. Наугад вынимают один шар. Какова вероятность того, что номер этого шара будет простым числом?

5.      Из 8 мальчиков и 5 девочек надо выделить для работы на пришкольном участке З мальчиков и 2 девочек. Сколькими способами это можно сделать?

6.      На четырех карточках написаны цифры 1, З, 5, 7. Карточки перевернули и перемешали. Затем наугад последовательно положили эти карточки в ряд одну за другой и открыли. Какова вероятность того, что в результате получится число, большее 7000?

Вариант 2                                   (S 11, 12)

• 1. Сколько шестизначных чисел можно составить из цифр 1, 2, З, 5, 7, 9 без повторения цифр?

•2. Из 8 учащихся класса, успешно выступивших на школьной олимпиаде, надо выбрать троих для участия в городской олимпиаде. Сколькими способами можно сделать этот выбор?

^о з. Из 15 туристов надо выбрать дежурного и его помощника. Сколькими способами это можно сделать?

⁰ 4. Из 30 книг, стоящих на полке, 5 учебников, а остальные художественные произведения. Наугад берут с полки одну книгу. Какова вероятность того, что она не окажется учебником?

5.      Из 9 книг и 6 журналов надо выбрать 2 книги и З журнала. Сколькими способами можно сделать этот выбор?

6.      На пяти карточках написаны буквы «о», «у», «к», «н», «с». Карточки перевернули и перемешали. Затем наугад последовательно положили эти карточки в ряд одну за другой и открыли. Какова вероятность того, что в результате получится слово «конус» или «сукно»?

(S 11, 12)

• 1, Сколькими способами можно определить последовательность выступления 8 участников конкурса вокалистов?

⁰ 2. Из 12 членов правления садоводческого кооператива надо выбрать председателя и его заместителя. Сколькими способами это можно сделать?

^о з. Из 19 членов бригады, прибывшей для ремонта школы, надо выделить троих для ремонта кабинета физики. Сколькими способами это можно сделать?

•4. Из 25 билетов по геометрии Андрей не успел подготовить 2 первых и З последних билета. Какова вероятность того, что ему достанется подготовленный билет?

5.      Из 15 юношей и 12 девушек, прибывших на соревнования по биатлону, тренер должен выделить для участия в смешанной эстафете 2 юношей и 2 девушек. Сколькими способами он может это сделать?

6.      На карточках записаны все возможные четырехзначные числа, составленные из цифр 1, 2, З, 4, без повторения. Карточки перевернули и перемешали, а затем открыли одну из них. Какова вероятность того, что на этой карточке окажется четное число?

Вариант 4                                   (S 11, 12)

•1. Сколькими способами можно составить расписание уроков на понедельник, когда изучаются литература, алгебра, геометрия, история, география, причем сдвоенных уроков нет?

•2. Сколько прямых можно провести через 10 точек, никакие три из которых не лежат на одной прямой?

^о з. Из 30 участников собрания надо выбрать председателя, его заместителя и секретаря. Сколькими способами это можно сделать?

•4. В пакете лежат жетоны с номерами 1, 2, З 20. Наугад берут один жетон. Какова вероятность того, что номер, написанный на нем, будет простым числом?

5.      Из 10 юношей и 12 девушек, прибывших на соревнования по теннису, тренер должен выделить 2 юношей и 2 девушек для участия в соревнованиях пар. Сколькими способами он может это сделать?

6.      На четырех карточках написаны буквы «о», «у», «к», «м». Карточки перевернули и перемешали. Затем наугад последовательно положили эти карточки в ряд одну за другой и открыли. Какова вероятность того, что в результате получится слово «мука» или «кума»?

К—9 (итоговая)

01. Упростите выражение

•2. Решите систему уравнений

ОЗ. Решите неравенство З + х 8х — (3х + 7).

      04. Упростите выражение        —6

а х ² — 5х +60,

5.      Решите систему неравенств

6.      Постройте график функции у = х ² — 4. Укажите, при каких значениях х функция принимает положительные значения.

7.      В фермерском хозяйстве под гречиху было отведено два участка. С первого собрали 105 ц гречихи, а со второго, площадь которого на З га больше, собрали 152 ц. Найдите площадь каждого участка, если известно, что уроэкайность гречихи на первом участке была на 2 ц с 1 га больше, чем на втором.

Вариант 2                                                        К—9 (итоговая)

Упростите выражение

Решите систему уравнений

ОЗ. Решите неравенство 6х — 8 10х — (4 — х).

      •4. Упростите выражение          -1

х х ² —6х +8 О,

5.      Решите систему неравенств

6.      Постройте график функции у = —х² + 1. Укажите, при каких значениях х функция принимает отрицательные значения.

7.      Из пункта А в пункт В, расстояние между которыми 45 км, выехал велосипедист. Через 30 мин вслед за ним выехал второй велосипедист, который прибыл в пункт В на 15 мин раньше первого. Чему равна скорость каждого велосипедиста, если известно, что скорость первого на З км/ч меньше скорости второго?

К—9 (итоговая)

Упростите выражение

т + 5 х +2у = 11,

02. Решите систему уравнений

ху = 14.

ОЗ. Решите неравенство 5х — З (х — 1,5) < 4х + 1,5.

04. Упростите выражение

а

5.      Решите систему неравенств

6.      Постройте график функции у = х² — 2х. Укажите, при каких значениях х функция принимает отрицательные значения.

7.      В фермерском хозяйстве благодаря применению новых технологий урожайность пшеницы возросла на З ц с 1 га. В результате было собрано не 190 ц пшеницы, как в предшествующем году, а 198 ц, хотя под пшеницу отвели на 1 га меньше. Какая площадь была отведена в хозяйстве под пшеницу в эти годы?

Вариант 4                                                        К—9 (итоговая)

01. Упростите выражение

•2. Решите систему уравнений

ОЗ. Решите неравенство х — 2,5 (2х — 1) > х — 1,5.

(х • х ¹⁶

      •4. Упростите выражение         —4

х х2 + Х-42<0,

5.      Решите систему неравенств

6.      Постройте график функции у = х ² + 2х. Укажите, при каких значениях х функция принимает положительные значения.

7.      Расстояние между городами А и В равно 120 км. Из города А в город В выехал автобус, а через 15 мин вслед за ним отправился автомобиль, скорость которого была на 12 км/ч больше скорости автобуса. Найдите скорость автобуса, если известно, что он прибыл в город В на 5 мин позже автомобиля.

итоговый т Ест

1.   Сколько общих точек имеют парабола у = х² — 6х + 5 и прямая у = 21?

             А. Ни одной Б. Одну             В. две           Г. три

2.   В какой координатной четверти расположена вершина параболы у = 6х² — х — 25?

          А. В первой         Б. Во второй

В. В третьей Г. В четвертой

З. В каких координатных четвертях расположен график -1,6 функции у = х

А. В первой и третьей Б. Во второй и четвертой В. В первой и второй Г. В третьей и четвертой

4.       Решите уравнение 4х⁴ — 5х² + 1 = о. Ответ:

5.       Найдите область определения функции у = 12-8х+х2 . Ответ:

6.       Найдите множество решений неравенства

(х ² - 16) (х - 5) < о.

в. (-4; 4) и (5; +00) г. (-оо; -4) U (4; 5) х ² — 5у = —11,

7.       Решите систему уравнений

х+у = -1.

Ответ:

8.       Какое из данных чисел не является членом арифметической прогрессии 12; 15; 18А. ЗО Б. 36 в. 42 г. 56

9.       Известно, что (ьп) — геометрическая прогрессия, в которой bl = 96 и q = — —. Какое из неравенств не являет4 ся верным?

10.   Сравните (п + 1)! п и п! (п + 1), где п — натуральное число.

Г. Ответ зависит от значения п

11.   Из 16 спортсменок тренер должен выделить четырех для участия в соревнованиях. Сколькими способами он может это сделать? Какой вид комбинаций рассматривается в этой задаче?

        А. Перестановки        Б. Размещения

        В. Сочетания                Г. Ни один из указанных видов

12.   Из 32 экзаменационных билетов Игорь не успел подготовить З первых и 5 последних. Какова вероятность того, что ему достанется подготовленный билет?

1 з 29 27 Б.           в.

              4            4             32             32

Вариант 2

1.    Сколько общих точек имеют парабола у = х² — 4х + 6 и прямая у = 11?

       А. Ни одной           Б. Одну           В. две          Г. три

2.    В какой координатной четверти расположена вершина параболы у = 2х ² + 3х — 5?

      А. В первой          Б. Во второй

      В. В третьей          Г. В четвертой

З. В каких координатных четвертях расположен график 0,9

функции у = х

А. В первой и третьей Б. Во второй и четвертой В. В первой и второй Г. В третьей и четвертой

4.        Решите уравнение 9х⁴ — 10х ² + 1 = О. Ответ:

5.        Найдите область определения функции у — 10- 7Х+х2

Ответ:

6.        Найдите множество решений неравенства

г. (-4; -3) U (3; +00)

7.        Решите систему уравнений у ² — ху = 33, х— у = 11.

Ответ:

8.        Какое из данных чисел не является членом арифметической прогрессии 16; 20; 24'

                      Б. 52         В. 68         г. 94

9.        Известно, ЧТО (bn) — геометрическая прогрессия, в ко-

1

торой Ь = —128 14  Какое из неравенств не является верным?

10.   Сравните (п + 2)! (п + 1) и (п + 1)! (п + 2).

Г. Ответ зависит от значения п

11.   Из 15 спортсменок тренер должен выделить четырех для участия в эстафете, указав при этом, кто побежит на первом, втором, третьем и четвертом этапах. Сколькими способами он может это сделать? Какой вид комбинаций рассматривается в этой задаче?

          А. Перестановки        Б. Размещения

           В. Сочетания               Г. Ни один из указанных видов

12.   В доме 80 квартир, из которых 4 находятся на первом этаже и 6 — на последнем. Квартиры распределяются по жребию. Какова вероятность того, что жильцу не достанется квартира, расположенная на первом или на последнем этаже? 1        1          з          7        Б.         в.

                     8                20                                           8

ИТОГОВОЕ ПОВТОРЕНИЕ ПО ТЕМАМ

Функции

1.    Что называется функцией? Найдите f(O); f(5); f(—1,5) для функции, заданной формулой:

                    б) f(x) = 2х ² + х — З.

2.    Что называется областью определения функции? областью значений функции? Что называется графиком функции? Постройте график функции и укажите область определения и область значений этой функции:

                                                                           6                    -8

а) у = 5х — 4;                                                б) у = 3,5х; х        х

З. Найдите область определения функции, заданной формулоЙ:

     а)        1,7х - 0,03;       

4.        Какие функции называются возрастающими в промежутке? убывающими в промежутке? Постройте график функции и укажите промежутки возрастания и промежутки убывания функции:

                                                                    12                   —4

                                                                     х                     х

5.        Является ли возрастающей или убывающей линейная функция:

      -4,2х + 8,1;      б) у = х — 4,3;      в) у = 6,2?

6.        Сформулируйте теорему о разложении на множители квадратного трехчлена. Разложите на множители квадратный трехчлен:

       а) 4х ² + 11х — З;         6) -2х ² - 9х + 18;

       в) 5х² — 30х + 45;        г) 18х² - 33х + 14.

7.        Сократите дробь:

2х ² + 13х -24      5х ² + 34х -7 а)б)

25х ² - 10х+ 1

8.        Дайте определение квадратичной функции. Как называется график квадратичной функции?

9.        Постройте график функции:

       а) у = 0,5х ² ;       6)        -0,4х ² .

10.    Сформулируйте свойства функции у = ах² при а > О; при а < О.

11.    Изобразите схематически график функции и укажите, в каких координатных четвертях он расположен:

         а) у = 6х² + 4;              б) у = —4х² — 5;

в) у = (х — 8)² ;

12.    Постройте график функции:

                                                6)         -2х² + 8;

                     2х - 8х - 10;           г) у = х² + 4х + 7.

13.    Какую функцию называют степенной функцией с натуральным показателем? Приведите примеры.

14.    Сформулируйте свойства степенной функции с четным показателем п. Покажите схематически график этой функции.

15.    Функция задана формулой f(x) = х ¹² . Сравните с нулем: а) [  в) f(O); г) f(—O,05).

16.    Функция задана формулой g (х) = х ¹⁰ . Сравните:

        а) g(5,6) и g(7,6);          б) g(10,2) и (10,6);

        в) g(—2) и g(—4);          

17.    Сформулируйте свойства степенной функции с нечетным показателем п. Покажите схематически график этой функции при п > 1.

18.    Функция задана формулой f (х) = х ^и . Сравните с нулем: а) [ (2,5);в) f(—1,5).

19.    Функция задана формулой f (х) = х?. Сравните:

а) [ (1,4) и f(1,6);

в) f(—1,5) и f(O);

20.    Дайте определение арифметического корня п-й степени из числа а. Является ли:

а) число — арифметическим корнем четвертой степени

1 из числа

81' 1 б) число — арифметическим корнем третьей степени

5

1 из числа

125

21.    Найдите значение выражения: а) ^з 216;з

8'

д) -0,501; е)

Уравнения и неравенства с одной переменной

1.    Какое уравнение называется целым? Приведите пример.

2.    Что называется степенью целого уравнения с одной переменной? Определите степень уравнения

(х ² - 8) (3х ³ - 4х) = 3х ⁵ . З. Решите уравнение:

а) (2х + 4) (3х - 1) - (6х - 12) (х + 3) = 100;

6)

4.         Как зависит число корней квадратного уравнения от его дискриминанта? Определите, при каких значениях К:

а) уравнение 3х ² + Кх + 12 = О имеет два корня;

б) уравнение 3х² + 6х + К = О имеет один корень;

в) уравнение 15х ² + Кх + 60 = О не имеет корней.

5.         Решите уравнение, используя разложение на множители:

           а) 0,28х⁴ - 0,07х ² = О;         6) 3х³ + 8х² - 15х - 40 = о.

6.         Решите уравнение, используя метод введения новой переменной:

а) (х ² + 2х) ² - 10 (х ² + 2х) + 21 = О;

б) (х ² + х + 1) (х² + х + 4) = 50.

7.         Какое уравнение называется биквадратным? Сколько корней может иметь биквадратное уравнение? Решите уравнение:

             а) х⁴ - 11х ² - 80 = о;             6) 9х⁴ + 17х²                        о;

в) (2х² - 1) (2х ² + 1) - 12 (х ² + 7) = 131

8.         Решите графически уравнение х ^з + х — 4 = О.

9.         Решите уравнение:

                          2               2           4х ² — 5

а)  б) • 1+2х 1-2х 4х ² - 1' 5+2х 5—2х 4х ² - 25

10.     Решите уравнение, используя введение новой переменной:

                       1                1                 4

а) х ² + 4х — 2 х ² + 4х х ² + 4х —3

6)

11, Какое из данных выражений принимает положитель ные значения при любых значениях х?

            А. х² — 6х + 1                 Б. х² + 16х

              в. х² - 8х + 12                 г. х ² - 12х + 40

12.   Решите неравенство:

          а) - 16 > О;                       6) -х² - 12 < о;

        в) х² > 3х;                           г) х² < 25;

          д) - 22х + 121                  е) х² - 12х + 36

13.   Найдите область определения функции:

14.   Решите неравенство, используя метод интервалов:

а) (х + 6) (х - 11) > О; 6) (х - 0,1) (х + 0,8) < о;

в) (х + 4) (х + 2) (х - 10) < о;

15.   При каких значениях х:

а) произведение (х + 7) (х — 8) положительно;

б) произведение (х — 4) (5х — 12) отрицательно; в) дробь           положительна;

3х+6

2х-8 г) дробь  отрицательна?

Х 11

16.   Решите систему неравенств:

          х ² + 2х-15<0,         3х ² +17х-6>0,

         а) х ² —16>0;                    6) 5х ² - 11х +2<0.

17.   Решите неравенство:

3х-5    5х—1 а)          6)

             6—х                     3-2х

в)  г) 2х-1

18.   Найдите целые решения системы неравенств:

                2х ² + о,                 3х ² + 11х -42 о,

          а) 9х ² - 1 > 0;                  б) 4х ²                       о.

Уравнения и неравенства с двумя переменными

1.    Что называется решением уравнения с двумя переменными? При каких значениях а:

а) пара чисел (а; З) является решением уравнения

б) пара чисел (2; а) является решением уравнения 17?

2.    Что называется графиком уравнения с двумя переменными? Какая фигура является графиком уравнения — (у ² + 1) = О? Выберите верный ответ.

          А. Парабола             Б. Гипербола

          В. Окружность         Г. Пара прямых

З. Запишите уравнение окружности, если известно, что:

а) центр окружности находится в точке (1; 4) и окружность касается оси х;

б) центр окружности находится в точке (2; З) и окружность касается оси у.

4.        Что называется решением системы уравнений с двумя переменными? Является ли пара чисел х = —5, у = 4 решением системы уравнений: х2 —у2 = 9, х ² + 3ху = 5,

а)б)

ХУ = —20?

5.        Решите графически систему уравнений:

а) х ² + у ² = 9, б) У = 2-х2 х ² + у

6.        Изобразив схематически графики уравнений, выясните, имеет ли решение система уравнений:

а) х ² + у ² = 16, 6) У = 5х2 в) (х -3) ² + (у -1) ² = 25, х — у = 10; ху = 8; у = 3х ² + 20.

7.        Решите систему уравнений:

х + Зу = 5,

                      а)б)                      ² — ху + у2 = 73;

х 2х+у = 7,

2х2 - у2 231

в)г) 2х ² + у ² 41

8.        Решите задачу.

а) Прямоугольный участок земли площадью 4800 м ² обнесен изгородью, длина которой равна 280 м. Найдите длину и ширину участка.

б) Периметр прямоугольника равен 20 см. Если длину прямоугольника увеличить на 2 см, а ширину уменьшить на 1 см, то площадь прямоугольника увеличится в 1,25 раза. Найдите стороны прямоугольника.

9.        Изобразите на координатной плоскости множество решений неравенства:

10.   Задайте неравенством с двумя переменными:

а) круг с центром в точке (О; 1) и радиусом, равным 5;

б) множество точек, расположенных вне круга с центром в точке (—4; 2) и радиусом, равным 5.

11.   Какую фигуру задает на координатной плоскости система неравенств: х ² + у ² < 16,

а)

12.   Изобразите на координатной плоскости множество решений системы неравенств:

а)

Арифметическая и геометрическая прогрессии

1.    Выпишите первые шесть членов последовательности:

а) натуральных чисел, кратных 6, взятых в порядке возрастания; б) квадратов натуральных чисел, взятых в порядке возрастания.

2.    Найдите первые пять членов последовательности (ап), заданной формулой п-го члена:

З. Найдите первые пять членов последовательности (ап), заданной рекуррентным способом:

           а) = 20, а              2 '    3, ап + 1 = (—1)^п ап.

4.        Дайте определение арифметической прогрессии. Выпишите первые пять членов арифметической прогрессии, первый член которой равен 37, а разность равна 4.

5.        Запишите формулу п-го члена арифметической прогрессии. В арифметической прогрессии (а п) найдите:

а) аи, если а

б) аш, если = 0,8, d = —0,2.

6.        Является ли членом арифметической прогрессии 12; 7• число —58? число —76? При положительном ответе укажите номер члена.

7.        Докажите, что последовательность (ап), заданная формулой ап = Кп + Ь, — арифметическая прогрессия. Является ли арифметической прогрессией последовательность, заданная формулой:

а) ап = Зп — 1; б) ап = —n + 16; В) ап = 0,4n; г) ап = 14n ² ;

З

8.        Запишите формулу суммы первых п членов арифметической прогрессии. Найдите сумму первых шести членов арифметической прогрессии:

а) 1,5; 4,5; 7,5•

9.        Вычислите сумму первых десяти членов арифметической прогрессии (оп), в которой:

                    6) = 0,4, а = -0,2.

10.    Найдите сумму всех натуральных чисел:

а) от 50 до 70 включительно;

б) от 25 до 75 включительно.

11.    Дайте определение геометрической прогрессии. Выпишите первые пять членов геометрической прогрессии, в которой первый член равен 72, а знаменатель равен 0,5.

12.    Запишите формулу п-го члена геометрической прогрессии. В геометрической прогрессии (ь п) найдите:

               а) b5, если = 2, q                       б) Щ, если b1 = 2 q

13.    Запишите формулу суммы первых п членов геометрической прогрессии. Найдите сумму первых шести членов геометрической прогрессии:

              а) 12; -6; З,                    6) -10; 20; -40,

14.    Найдите сумму первых шести членов геометрической прогрессии (Щ), в которой:

              12,            -2;

Элементы комбинаторики и теории вероятностей

1.    Что называется:

а) перестановкой из п элементов;

б) размещением из п элементов по К;

в) сочетанием из п элементов по К?

2.    Из 24 учащихся класса надо выделить четверых для работы на пришкольном участке. Сколькими способами можно это сделать? Какой вид комбинаций рассматривается в этой задаче? Выберите верный ответ.

А. Перестановки Б. Сочетания

        В. Размещения          Г. Ни один из этих видов

З. Сколько пятизначных чисел, в записи которых цифры не повторяются, можно составить из цифр О, 2, 4, 6, 8? Укажите наименьшее и наибольшее из них.

4.        Найдите значение выражения: а)      ,           б) А 4³ +

5.        Делится ли число 14! на: а) 84;          6) 38?

6.        Решите уравнение:

1

       а)              = 380;       6) (п 8)! — 306 •

7.        На полке надо разместить 10 различных пособий по алгебре, из которых четыре — сборники задач, причем сборники задач должны стоять рядом. Определите число возможных способов.

8.        Десять девочек должны разместиться на десятиместной скамье так, чтобы входящие в их число Катя, Вера и Юля сидели рядом, причем Юля сидела бы между Катей и Верой. Определите число возможных комбинаций.

9.        Сколькими способами из 12 книг и 10 журналов, рекомендованных библиотекарем, читатель может выбрать З книги и 2 журнала?

10.   На плоскости отметили несколько точек, никакие три из которых не лежат на одной прямой, и провели через них все возможные прямые. Если исключить четыре из этих точек, то число прямых, которые можно провести через все точки, уменьшится на три. Сколько точек было отмечено на плоскости?

11.   Староста класса рассчитал, сколькими способами он может назначить двух дежурных для уборки класса. Однако в этот день четверо его одноклассников не пришли в школу, и число возможных способов назначения дежурных уменьшилось в 1— раза. Определите число учащихся в классе.

12.   Как вычисляется вероятность случайного события при классическом подходе? Какое событие называется невозможным? Чему равна вероятность невозможного события? Какое событие называется достоверным? Чему равна вероятность достоверного события?

13.   В телевизионной игре «Что? Где? Когда?» стрелка остановившегося волчка указывает на один из секторов с номерами 1, 2 13. Какова вероятность того, что стрелка укажет на сектор, номером которого является: а) простое число; б) число, кратное З?

14.   Из 30 экзаменационных билетов по истории Ирина успела подготовить 27 билетов, а Ольга только 24 билета. Какова вероятность того, что неподготовленный билет достанется Ирине? достанется Ольге? Может ли случиться так, что Ирине достанется неподготовленный билет, а Ольге — подготовленный?

15.   На четырех карточках написаны буквы «к», «с», «т», «у». Карточки перевернули, перемешали, а затем положили в ряд одну за другой и открыли. Какова вероятность того, что в результате получится слово «куст» или «стук»?

16.   Семь членов туристической группы распределяют по жребию дни дежурства на следующей неделе. Какова вероятность того, что Игорь, принимающий участие в жеребьевке, будет дежурить в субботу или в воскресенье?

17.   В пакете лежат жетоны, на которых записаны всевозможные двузначные числа, составленные с помощью цифр З, 4, 5, 6, одинаковых или различных. Наугад берут один жетон. Какова вероятность того, что на нем окажется число, записанное двумя одинаковыми цифрами?

18.   В квадрате ABCD проведен отрезок ЕЕ, где точка Е — середина стороны АВ, точка F — середина стороны ВС. Какова вероятность того, что случайным образом выбранная точка квадрата ABCD окажется принадлежащей треугольнику ЕВЕ?

19.   На полке стоят одинаковые по форме и размеру несколько желтых и 9 синих кружек. Зная число желтых кружек, можно вычислить вероятность того, что взятая наугад в темноте кружка окажется желтой. Если бы желтых кружек было на З больше, то вероятность взять с полки в темноте желтую кружку увеличилась бы на 0,15. Сколько желтых кружек стоит на полке?

ЗАДАНИЯ ДЛЯ ШКОЛЬНЫХ ОЛИМПИАД

Осенняя олимпиада

1.                        Двузначное число больше произведения его цифр на 12. Найдите это число.

2.                        Докажите, что если дробь      , где а и Ь — некоторые на-

туральные числа, причем а > Ь, несократима, то несократима а также и дробь

З. Постройте график функции у = х + х

4.                   Докажите, что при любом натуральном п > 1 верно неравенство

                            1       1            1 1

5.                   Решите уравнение (1 + х² ) ² = 4х (1 — х² ).

6.                   Решите неравенство х — 1 + х + 2 З.

7.                   Из пункта А вышел пешеход, а из пункта В навстречу ему одновременно выехал велосипедист. Они встретились в 6 км от пункта А, и в тот момент, когда велосипедист прибыл в пункт А, пешеходу осталось пройти до пункта В еще 16 км.

Найдите расстояние от А до В.

8.                   Постройте график уравнения х²у² — 9х² — 4у² + 36 = О

Весенняя олимпиада

1.   Разложите на множители многочлен х^б — х ⁵ + х

2.   Докажите, что при любых х и у верно неравенство 2х² + 2ху + 4у² + 2х + бу + 5 1.

З. Графиком некоторого уравнения служит квадрат ABCD, где А (—1; О), В (О; 1), С (1; О), D (О; —1). Запишите это уравнение.

4.                   Решите уравнение:

а) x+G- = 3 1 х2

5.                   Последовательность (а п) задана формулой ап = 7^п + 12П. Докажите, что при делении любого члена этой последовательности на 18 в остатке получается 1.

6.                   Докажите, что верно равенство

3+J6+Ji+Ji+ 3-J6+Ji-Ji=J6+Ji.

7.                   Упростите выражение ³ 20 +   + ³ 20 — 14“.

8.                   Найдите натуральные значения х и у, при которых верно равенство х² — у² = 21.

Ответы к контрольным работам

К—1. В— 1. 1. При х = З; при х < З; при х > З. Функция f возрастающая. 2. а) (х — 5) (х — 9);

Зр +2

4. g(x) = О при х = 2, х = 6; g(x) < О при х е [—2; 2); g(x) > О при х е (2; 6). Функция убывает на отрезках [—2; О], [4; 6] и возрастает на отрезке [О; 4]. Область значений функции — отрезок

[—3; 2]. 5. При а = Ь = 25. В—2. 1. При х = 5; при х > 5; при Функция        убывающая.

4. f(x) = О при х = —3, х = 1, х = З;

f(x) <О при х е [—5; —3) U (1; З); f(x) > О при х е (—3; 1) U (З; 4]. Функция возрастает на отрезках [—5; —1], [2; 4] и убывает на отрезке [—1; 2]. Область значений функции — отрезок [—2; 4]. 5. При c=d= 35. В—З. 1. При х = З; при х < З; при х > З. Функция f возрастающая. 2. а) (х — 5) (х — 7); б) (7у — 2) (у + З). з.  4. (х) = О при х = 1, х = 5; f (х) < О при 5а + 1 х е [—1; 1) U (5; 6]; [ (х) > О при х е (1; 5). Функция убывает на отрезках [—1; О], [З; 6] и возрастает на отрезке [О; З]. Область значений функции — отрезок [—2; 2]. 5. при а = Ь = 23.

В—4. 1. При х = 4; при х > 4; при х < 4. Функция g убывающая. 2. а) (х - 3) (х - 15);  з.

7b+3

4. g(x) = О при х = —2, х = 1, х = 5; g(x) < О при х е [—3; —2) U U (1; 5); g(x) > О при х е (—2; 1). Функция возрастает на отрезках [—3; О], [З; 5] и убывает на отрезке [О; З]. Область значений функции — отрезок [—2; 2]. 5. При т = п = 31.

К—2. В— 1. 2. —9. З. [—22; З]. 4. Пересекаются в точках (4; 4) и (16; 64). 5. 18,5. В—2. 2. 5. З. [-11; -2]. 4. Пересекаются в точках (-20; 80) и (5; 5). 5. 10?. В—З. 2. -25. З. [-9; -5].

4.        Пересекаются в точках (З; З) и (15; 75). 5. 6 ² . В—4. 2. 7.

1

3'

1

5.        1;  12; 1-   в—з. 1. а) О; -6; 6; 6) -3,5; 5. 2. -5; -2;

2

1.   2; 5.

3'

1

4 1 а) О; -5; 5; 6) -1,5; З. 2. -6; -2; 2; 6. З. -2; 2. 4. а)

6'

К—4. В— 1. 1. а) (—1; 4,5); б) (—оо; —7) U (7; +00); в) (—оо; +00).

1

2.   (—оо; —3) U (4; 6). З. При т < —12 и т> 12. 4. а)

5 '

б) (-оо; -8) И [17; +00). 5. а) [0; 31; 6) (-оо; -2] 0[6; 9) +00); в) [—4; 1,4]. В—2. 1. а) (—оо; —2) U 3 ² ; +00 ; б) (—9; 9); в) решений

нет. 2. (-оо; -5) U (1•, 4). З. при -20                                       4. а) (-оо; -2) U

+00); б) (—оо; —8] U (—5; +00). 5. а) [О; 1,251; б) (—оо; —10] U U[8; 12) U (12; +00); в) 2,5]. в—з. 1. а) (0,5; 6); оо; —3) U (З; +00); в) (—оо; +00 . 2. (-8; -1) U (4; +00). З. при

1

                                  ( 5                 6) [-10; -4). 5. а) О;

+00); в) [0; 1,2]. В—4. 1. а) (-оо; -1,6) U 00; +00). 2. (-оо; -10) И 5). З. при 4

-10 <        10. 4. а) (-1,5; 8); 6) (-оо; -14] U          +00). 5. а) О

9

б) (-оо; -10] U [-2; 26) U (26; +00); в) [0; 1,6].

К—5. В—1. 1. -3), (5; 2). 2. 5 и 12 см. З. (1; 2), (0,4; 2,2).  (3,6; 9). в—2. 1. (-6; 28), и 4 см. з. (-5; 11),  (3; 6). в—з.

—5 . 2. 5 и 9 см. з. (1; -4), (4; 1). 5.                       -36), (12; 6).

4 1. (-3; -1), (3,2; 0,24). 2. 6 и 7 см. З. (-4; 8), (3; 1). 5. (6; 12), (7,2; 18).

К—6.   в—1. 1. 91.      2. 345. З. да.   5. 2812. в—2. 1. -79. 2. 970. З. да. 4. 1365. 5. 1053. В—З. 1. 51.

2. -352. З. да. 4. 7200. 5. 1617. В-—4. 1. 159. 2. -427. З. да. 4. 21 540. 5. 324.

К—7. в—1. 1. 0,0015. 2. 20. з. 15?. 4. 0,002 или -0,002.

5. 765.          . 1. -27 000. 2.     з. 29 484. 4. 5000. 5. 728 1

в—з. 12. 12. з. 4080. 4. 1,2. 5. -1705. в--4. 1. -0,2. зоо•

2. з. з. 20,44. 4. 1,6. 5. 31-

К—8. В—1. 1. 120 способами. 2. 60 чисел. З. 45 способами. 9

5. 560 способами. 6.1. 720 чисел. 2. 56 способа-

                                                  5                                              1

ми.          З. 210 способами.	4.                 5. 720 способами.          6.       • 60
В—З. 1. 40 320 способами.	2. 132 способами. З. 969 способами.
4 5. 6930 способами. 6.	В—4. 1. 120 способами. 2. 45 пря-

                                                              2                                                   1

мых. З. 24 360 способами. 4.                5. 2970 способами. 6.

К—9. В—1. 1. х - у. 2. (0; -1), (2; -3). З. [2,5; +00). 4.

5. [2; 2,5]. 6. при х                   и х > 2. 7. 5 и 8 га. В—2. 1.

2. (1; 0),                2). з. (-оо; -0,8]. 4. В. 5.  . 6. при х

5

и х > 1. 7. 12 и 15 км/ч. В—з. 1.2. (7; 2), (4; 3,5).

6. при 7. 10 и 9 га.

(-оо; 0,8). 4. х² . 5. 1 6

6. При х < —2 и х > О. 7. 60 км/ч.

Ответы и указания к заданиям олимпиад

Осенняя олимпиада

1. 28 и 39. 2. Указа ни е. Предположить, что дробь сократи-

ма, т. е. а = ЧК и Ь = blk, где К 1 — натуральное число. З. График — объединение лучей у = О, где х < О, и у = 2х, где х > О.

1   1          1          1          1          1          1 4. Указание.          

где п > 1. 5. —1—0; —1 + а. 6. [—2; 1]. 7. 24 км. 8. График уравнения — объединение четырех прямых: х

Весенняя олимпиада

1. (х² — х + 1) (х⁴ — х ² + 1). 2. Указание. Представить левую

часть неравенства в виде суммы трех квадратов двучленов. 9 б) а —1 6+1

6. Указание.

                                          16'          2            2

При упрощении подкоренных выражений воспользоваться тождеством (а + Ь + с)² = а² + 6² + с² + 2ab + 2ас + 2bc. 7. 4. 8. х = 5, у = 2 или х = 11, у = 10.

СОДЕРЖАН ИЕ

Предисловие

Самостоятельные работы

Вариант I

Вариант П33 Контрольные работы .61

Итоговый тест81

Итоговое повторение по темам. 84

Задания для школьных олимпиад .93

Ответы к контрольным работам. 94 Ответы и указания к заданиям олимпиад96

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКТ

ПО АЛГЕБРЕ ДЛЯ 7-9 КЛАССОВ СОДЕРЖИТ:

Рабочие программы. 7—9 классы (автор Н.Г. Миндюк)

Учебники для 7, 8 и 9 классов

(авторы Ю.Н. Макарычев, НГ. Миндюк, К.И. Нешков,

С.Б. Суворова; под ред. СА. Теляковского)

Рабочие тетради е 7 класс (авторы Н.Г. Миндюк, И.С. Шлыкова)  8 класс (авторы Н. Г. Миндюк, И.С. Шлыкова)  9 класс (авторы Н.Г. Миндюк, И.С. Шлыкова)

гичек кие ма гериа. ' ы

•   7 класс (авторы Л. И. Звавич, Л. В. Кузнецова, С.Б. Суворова)

•   8 класс (авторы В.И. Жохов, Ю. Н. Макарычев, Н. Г. Миндюк)

•  

9 к. 'а« (авл оры Н) Н. Ма ка рычев, ра и нева ;

Тематические тесты е 7 класс (авторы Ю. П. Дудницын, В.Л. Кронгауз) о 8 класс (авторы Ю.П. Дудницын, В.Л. Кронгауз)

•   9 класс (авторы Ю. П. Дудницын, В.Л. Кронгауз)

                Книги для учителя

•   Изучение алгебры в 7—9 классах (авторы Ю.Н. Макарычев,

Н.Г. Миндюк, С. Б. Суворова, И.С. Шлыкова)

•   Уроки алгебры в 7 классе (авторы В. И. Жохов, Л.Б. Крайнева)  Уроки алгебры в 8 классе (авторы В. И. Жохов, Г. Д. Карташёва) е Уроки алгебры в 9 классе (авторы В. И. Жохов, Л.Б. Крайнева)

          lSBN 978-5-09-026766- з       

ПРОСВЕЩЕНИЕ

И З Д А Т Е Л ь с т в о

9 785090 267663