дидактикалық материал

1+ 2+ 3+ ... + 99+100

1. Тізбектегі бірінші мен соңғы мүшелердің қосындысы 101 болатынын, яғни  қосындының ұштарынан бірдей қашықтықтағы қосылғыштарды қосқанда әр қосындының 101-ге тең болатынын білген. 
2. 1-ден 100-ге дейінгі сандарды қос-қостан топтаған кезде 50 жұп алынатындығын ескерген.
3. Жұптар санын, яғни 50-ді 101-ге көбейтіп  5050 санын алады..

Демек, 1-ден 100-ге дейінгі натурал сандардың қосындысы 5050-ге тең.

     Осы пайымдауды қолданып, арифметикалық прогрессияның алғашқы n мүшесінің қосындысын есептеу формуласын қорытып шығарайық. Оны  арқылы белгілейік. Қосындыны өсу ретімен жазып, оның астына қосындыны кему ретімен сәйкестендіріп жазамыз:

Теңдіктерді мүшелеп қосатын болсақ:

Жақшалардың ішіндегі әр қосынды  -ге тең. Шынымен,

 Мұндай жұптардың саны n.

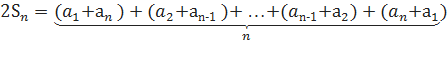
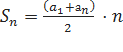                                              (1)

      Біз арифметикалық прогрессияның алғашқы  мүшесінің қосындысы туралы теореманы дәлелдедік.

Теорема.  Арифметикалық прогрессияның алғашқы  мүшесінің қосындысы шеткі мүшелерінің (арифметикалық ортасын) қосындысының жартысын  барлық мүшелер санына көбейткенге тең.

Осы формуладағы -ші мүшені  мен d

арқылы өрнектейік.    формуласын (1) формулаға қоятын болсақ:

                                                    (2)