
Содержание:
Введение 2
Глава1. МЕХАНИКА Г.ГАЛИЛЕЯ.
1. Теория движения Галилея. 5
2. Парадоксы теоретического мышления Галилея. 14
Глава 2. Механика И. Ньютона.
1. Вклад Ньютона в развитие естествознания. 17
2. Первый закон Ньютона. 19
3. Второй закон Ньютона. 20
4. Третий закон Ньютона 21
5. Фундаментальные законы движения Ньютона 22
6. Закон всемирного тяготения. 25
7. Законы Кеплера. 27
8. Границы применимости механики Ньютона. 31
Глава 3. Бэкон и Декарт.
1. Френсис Бэкон (1561—1626). 34
2. 'Начала философии' Рене Декарта. 37
3. Пространство и время. Специальная теория относительности 42
Заключение 45
Литература 48
Введение
С XVII века начинается период нового времени. Философия Возрождения подготовила новый тип философствования, отвергавший схоластику, теоцентристские построения, которые перестали удовлетворять требованиям объяснения новых социальных реалий. В XVII веке укрепился капиталистический способ производства. Развитие экономики требовало расчетов национального дохода, индивидуальных доходов, численности рождаемости и смертности и т.д. Предпринимательский расчет становится нормой повседневной жизни. Его основа - количественная оценка. Расчет, количественная оценка влияют на человеческие отношения, проникают во все сферы человеческой практики.
Университетская наука, увлеченная проблемами античности и занявшаяся отвлеченными от практических потребностей вопросами, оказалась своего рода "закрытой системой", изолировавшей себя от реальных потребностей общества. Поэтому развитие физики в это время осуществлялось преимущественно вне университетской науки.
В период нового времени возникновение интереса к опытному естествознанию во многом обязано Ф.Бэкону. Вместе с тем в условиях отставания теоретического естествознания от практических успехов техники важно было научное обобщение результатов технического опыта. Прежде всего, возникла необходимость в усовершенствовании методов измерения и технологических приемов создания физических аппаратов. Накопленный опыт в машиностроении имел важное значение, и его можно было использовать. Ситуация же в области теоретической физики была иной.
Физика в это время могла предлагать разного рода теоретические гипотезы качественного характера. Способы же формулировок теоретических задач в математической форме, позволявшие осуществлять расчеты с научной степенью точности, отсутствовали. Качественные гипотезы не могли быть положены в основу технологических процессов или конструктивных разработок. В этих условиях разрыв между более высоким экспериментальным уровнем физики и более низким уровнем физических теорий мог быть ликвидирован с помощью экспериментальной науки. (Метод теоретической физики будет создан Ньютоном позже, в конце XVII века). В этом русле и проявилась методология Бэкона, ориентировавшая на постановку экспериментов, способствующих открытию новых законов. Принцип количественного измерения в экспериментальных исследованиях становится основой естествознания. Это находит свое выражение в изобретении разнообразных измерительных приборов - хронометров, биометров, термометров, весов и т.д. Таким образом, вслед за машиностроительной отраслью возникает приборостроительная.
Важно отметить признание Декартом возможной неоднозначности физической теории, что явилось следствием познания, каким способом Бог реализовал данное физическое явление. Иначе говоря, соответствующая дедуктивным выводам теория оказывается лишь наиболее вероятной из числа возможных.
Иную позицию занимал Ньютон. Для него было важно однозначно выяснить с помощью экспериментов и наблюдений свойства изучаемого объекта и строить теорию на основе индукции без использования гипотез. Он исходил из того, что в физике как экспериментальной науке места для гипотез нет. Признавая небезупречность индуктивного метода, он считал его среди прочих наиболее предпочтительным.
Общим для Декарта, Ньютона и других исследователей природы этого времени было использование теологических аргументов. (Не случайно Ньютона иногда называет не только первым ученым, но и последним богословом.) Задача естествознания усматривалась в выявлении божественного плана творения природы. В этом заключалась специфика развития периода нового времени. Поскольку физика XVII века по необходимости вступала в противоречие с церковными догматами, церковь, отстаивавшая свою позицию различия небесной и земной физики, не могла остаться к этому равнодушно. Галилей был подвергнут церковным репрессиям за "Диалог о двух главнейших системах мира, птолемеевой и коперниковой", целью которых было стремление приостановить распространение коперниканских идей. Для Италии, выступавшей в числе лидеров научного прогресса, это имело негативные последствия - развитие физических идей было заторможено.
Наука Нового времени выдвигает новые идеалы и нормы исследования – научный эксперимент, опору на индукцию, интуицию, выдвижение гипотез и теорий и их проверку экспериментальным путем. Со времен Галилея и Ньютона идеалом научности становятся объективное, истинное знание о законах природы, идея расширения знания и вера в окончательное раскрытие всех тайн природы. «Знание - сила» – провозгласил идеал научности Ф.Бэкон. Сложилось представление о фундаментальном характере открытых законов, их абсолютной достоверности и неопровержимости.
Декарт оказал громадное влияние на последующую науку и философию. Европейские мыслители восприняли от него призывы к созданию философии как точной науки (Б. Спиноза), к построению метафизики на базе учения о душе (Дж. Локк, Д. Юм). Декарт активизировал и теологические споры в вопросе о возможности доказательств бытия Бога.
Глава1. МЕХАНИКА Г.ГАЛИЛЕЯ.
1. Теория движения Галилея.
Средневековая физика при рассмотрении движения исходила из двух фундаментальных принципов перипатетической кинематики: во-первых, всякое движение предполагает двигатель (omne quod movetur, ab aliquo movetur); во-вторых, любое тело оказывает сопротивление движению, это сопротивление должно быть преодолено, чтобы началось движение, и постоянно преодолеваемо, чтобы движение продолжалось (resistentia est causa successionis in motu - сопротивление есть причина последовательности в движении). Первое положение означает, что всякое движение нуждается для своего возникновения и сохранения в постоянно действующей силе. Второе положение по существу сводится к аристотелевскому тезису о невозможности движения в пустоте: там, где движущемуся телу не оказывалось бы никакого сопротивления, имело бы место не движение как последовательное изменение пространственного положения тела, протекающее во времени (motus), а мгновенное изменение (mutatio), происходящее вне времени, или, что то же самое, с бесконечной скоростью. Такого рода мгновенное изменение, как полагал Аристотель, должно было бы происходить в пустоте, а потому допущение пустоты разрушало бы всю систему перипатетической науки о движении. Закон, согласно которому "все движущееся движется чем-то", дополнялся в античной и средневековой физике положением, что состояние покоя для своего сохранения не нуждается ни в каком внешнем факторе. Тем самым утверждалась онтологическая неравноценность двух различных состояний: покоя и движения - неравноценность, имеющая свое обоснование в философском мышлении античности и коренящаяся в характерных особенностях мировоззрения древнего и средневекового человека. Движение мыслится Аристотелем как изменение состояния тела, а покой - как неизменность этого состояния. Движение и покой здесь - не относительные понятия, какими они стали в механике нового времени как раз благодаря Галилею, а понятия, так сказать, абсолютные: движется ли тело или покоится, это определялось не через отношение его к любому другому телу или системе тел, которые онтологически равноправны с первым, а по отношению к абсолютным точкам отсчета: центру и периферии космоса, т.е. абсолютному "низу" и "верху". С помощью абсолютных "верха" и "низа" вводилось существенное для античной и средневековой физики различение естественного и насильственного движений. Поэтому античная и средневековая физика в той мере, в какой она исходила из Аристотеля, предполагала конечный космос, в котором понятия верха и низа не только имели характер абсолютных ориентиров, но и различались между собой чисто физически: "верх" (надлунный мир, или, как его еще называли, небо) как по составу заполняющего его пятого элемента - эфира, так и по характеру движения небесных тел принципиально отличался от мира подлунного.
Но, пожалуй, едва ли не самым существенным изменением, внесенным в средневековье в аристотелевскую физику, была так называемая идея импетуса, или импульса, с помощью которой предполагалось объяснить движение брошенных тел, получившее весьма неудовлетворительное объяснение у Аристотеля. Метательное движение представляет большое затруднение для физики, которая исходит из того, что все движущееся движется чем-либо. В случае естественного движения тело как бы движется "местом": стремление к своему естественному месту (у тяжелых тел - к центру Земли, у легких - к периферии космоса, к небу) является "двигателем" тела. В случае насильственного движения, например, при поднятии тяжелых тел вверх или при передвижении их в горизонтальном направлении, это живая сила (лошадь, человек и т.д.) или же искусственно созданный агрегат, приводимый в действие либо природной стихией, либо опять-таки живой силой. Но как объяснить случай "насильственного" движения брошенного тела, на которое больше не воздействует двигатель, но которое, тем не менее, еще продолжает двигаться? Согласно Аристотелю, при метательном движении имеет место передача движения через ближайшую к телу среду: бросающий приводит в движение не только брошенное тело, но и воздух, который в состоянии некоторое время приводить в движение тело, являясь, таким образом, промежуточным двигателем.
Теория импетуса получает развитие в позднесхоластической натурфилософии XIV в., сначала в Парижской, а затем и в Оксфордской школах. Здесь она превращается в научную теорию, впоследствии получившую название "физики импетуса", главным образом благодаря Жану Буридану, Николаю Орему, Альберту Саксонскому и Марсилию из Ингена (первому ректору Гейдельбергского университета). В XV в., как показывает Аннелиза Майер, физика импетуса получает всеобщее признание, а к концу XVI в., как раз когда формируются научные воззрения Галилея, она становится широко известной. "Долгое время господствовало мнение, - пишет А. Майер, - и еще по сей день оно распространено, что в схоластической теории импетуса implicite содержится закон инерции, и что поэтому начала классической механики следует искать в XIV в. ...В теории импетуса, как она была сформулирована в XIV в., еще нет никаких идей, в которых был бы хотя бы намек на то, что позднее было названо законом инерции; однако она содержит ряд допущений, которые могли привести и в самом деле привели к открытию закона инерции".
Поскольку нас интересует та трансформация фундаментальных понятий физики, которую произвел Галилей, мы вкратце охарактеризуем физику импетуса, как она сложилась к его времени.
Представителем физики импетуса был непосредственный предшественник Галилея Дж. Бенедетти, работа которого "Различные математические и физические рассуждения" была издана в Турине в 1585 г., как раз в то время, когда формировались научные интересы молодого Галилея. Бенедетти интересовал вопрос о причинах возрастания скорости падающих тел, которым впоследствии занялся Галилей. Физика импетуса вплотную подошла к открытию закона инерции, и в ней наметился тот путь, каким затем пошел Галилей: в своем сочинении "О движении" он выступает как критик аристотелевской динамики с точки зрения динамики импетуса, как убедительно показал А. Койре. Сам Галилей в ранний период опирался на теорию импетуса, а впоследствии придал ей ту форму, в которой уже и в самом деле содержался принцип инерции.
Изучение метательного движения непосредственно подводит физику XIV-XVI вв. к рассмотрению свободного падения тел как наиболее уникальному случаю, где как бы снимается различие естественного и насильственного движений. И в самом деле, если брошенное вверх тело движется насильственно под воздействием сообщенного ему импульса, то, остановившись затем на мгновение, оно падает назад уже под воздействием силы тяжести. Это его падение, казалось бы, ничем не отличается от падения камня с горы. В том и в другом случае у физиков возникал вопрос: чем объяснить различие скорости падающего тела в начале и в конце движения? В случае метательного движения могло возникнуть предположение: не играет ли тут какую-то роль тот импульс, который двигал тело вверх? Не оказывает ли он в первые моменты падения некоторого сопротивления силе тяжести, тем самым противодействуя ей и замедляя движение тела? Но это означало бы, что импетус может сохраняться, как бы консервироваться в теле в тот момент, когда тело переходит в состояние покоя (в момент мгновенной остановки тела). Этого не могла допустить схоластическая физика в силу как раз принципиального различения естественного и насильственного движений, которое требовало различать также и характер сил, вызывающих эти два разных движения.
Допущение, что импетус может сохраняться в теле в состоянии покоя, сняло бы это принципиальное различие между неистощимой и истощимой силами, а тем самым появилась бы возможность сближения насильственного движения с естественным. Такое допущение и сделал Галилей. В своем раннем сочинении "О движении" он также рассматривает еще один интересный вариант движения под действием импетуса, а именно движение гладкого шара по горизонтальной гладкой плоскости, где как сила тяжести тела, так и сопротивление поверхности в расчет не принимаются, а действует только инерция сопротивления самого тела по отношению к насильственному двигателю. В этом случае, говорит Галилей, нужна минимальная сила, чтобы сохранять тело в движении; Галилей называет ее vis minor quam queris alia vis - "сила, меньшая всякой другой силы", или, как мы сказали бы сегодня, - бесконечно малая сила.
Здесь Галилей и в самом деле близко подходит к открытию закона инерции, причем применяет тот же ход рассуждения, что и при рассмотрении метательного движения: ибо импетус при движении тела на горизонтальной плоскости, как и при движении в воздухе, постепенно затухает, даже если допустить, что нет никакого внешнего сопротивления движению тела (т.е. что оно движется в пустоте). Открытию закона инерции содействует рассмотрение изолированного от остального универсума тела, на которое уже не действует само пространство ("верх" и "низ"), а действует только сила, содержащаяся в самом теле. Однако эта сила мыслится как сообщенная телу внешним двигателем, а потому и иссякающая по мере движения тела. Сделать следующий шаг в направлении к закону инерции и допустить, что тело может двигаться в раз данном ему направлении само по себе, не расходуя при этом никакого импетуса, а потому и не замедляя своего движения (при условии, что нет сопротивления среды), в рамках физики импето невозможно. Принцип тождества противоположностей руководит Галилеем при исследовании свободного падения тел. Здесь этот принцип позволяет Галилею снять противоположность покоя и движения, составлявшую краеугольный камень аристотелевской физики. "Если я представлю себе тяжелое падающее тело выходящим из состояния покоя, - пишет Галилей в "Беседах и математических доказательствах", - при котором оно лишено какой-либо скорости, и приходящим в такое движение, при котором скорость его увеличивается пропорционально времени, истекшему с начала движения... то невольно приходит на мысль, не вытекает ли отсюда, что благодаря возможности делить время без конца мы, непрерывно уменьшая предшествующую скорость, придем к любой малой степени скорости или, скажем, любой большей степени медленности, с которой тело должно двигаться по выходе его из состояния бесконечной медленности, т.е. из состояния покоя". Состояние покоя предстает теперь как состояние движения с бесконечно малой скоростью, оно теряет, таким образом, свое прежнее значение и становится - благодаря введению предельного перехода - в один ранг с движением. Правда, такое рассуждение идет вразрез с опытом, свидетельствующим о том, что падающее тело с первого же момента движется с большой скоростью. Это прекрасно известно и самому Галилею, и Сагредо тут же отмечает эту трудность. "...Если с той степенью скорости, которую тело приобретает за четыре удара пульса и которая в дальнейшем остается постоянной, оно может проходить две мили в час, а с той степенью скорости, которая приобретается после двух ударов пульса, оно может проходить одну милю в час, то надлежит признать, что для промежутков времени, все более и более близких к моменту выхода тела из состояния покоя, мы придем к столь медленному движению, что при сокращении постоянства скорости тело не пройдет мили ни в час, ни в день, ни в год, ни даже в тысячу лет; даже и в большее время оно не продвинется и на толщину пальца - явление, которое весьма трудно себе представить, особенно когда наши чувства показывают, что тяжелое падающее тело сразу же приобретает большую скорость".
Как видим, теоретическое построение у Галилея создается до всякого опыта и независимо от него - оно представляет собой решение задачи, правильность которого лишь задним числом должна быть подтверждена в опыте. Но посмотрим, как понимает Галилей опыт. Возьмем тот же пример, который приводит сам Галилей. "Вы говорите, - пишет Галилей, - что опыт показывает, будто падающее тело сразу получает весьма значительную скорость, как только выходит из состояния покоя; я же утверждаю, основываясь на том же самом опыте, что первоначальное движение падающего тела, хотя бы весьма тяжелого, совершается с чрезвычайной медленностью. Положите тяжелое тело на какое-нибудь мягкое вещество так, чтобы оно давило на последнее всей своей тяжестью. Ясно, что это тело, поднятое вверх на локоть или на два, а затем брошенное с указанной высоты на то же вещество, произведет при ударе давление большее, чем в первом случае, когда давил один только вес тела. В этом случае действие будет произведено падающим телом, т.е. совместно его весом и скоростью, приобретенной при падении, и будет тем значительнее, чем с большей высоты наносится удар, т.е. чем больше скорость ударяющего тела. При этом скорость падающего тяжелого тела мы можем без ошибки определить по характеру и силе удара. Теперь скажите мне, синьоры, если груз, падающий на сваю с высоты четырех локтей, вгоняет последнюю в землю приблизительно на четыре дюйма, - при падении с высоты двух локтей он вгоняет ее в землю меньше и, конечно, еще меньше при падении с высоты одного локтя или одной пяди, и когда, наконец, груз падает с высоты не более толщины пальца, то производит ли он на сваю больше действия, чем если бы он был положен без всякого удара? Еще меньшим и совершенно незаметным будет действие груза, поднятого на толщину листка. Так как действие удара находится в зависимости от скорости ударяющего тела, то кто может сомневаться в том, что движение чрезвычайно медленно и скорость минимальна, если действие удара совершенно незаметно?" Это обращение к "опыту" интересно не только тем, что Галилей предлагает создать особые условия для проведения опыта; как раз в данном случае опыт выглядит почти как наблюдение непосредственно происходящего в природе, "конструкция" опыта чрезвычайно проста; поразительно в этом опыте другое, а именно что Галилей не замечает, как его доказательство вращается в порочном круге. И в самом деле, почему понадобился Галилею этот опыт? Да потому что при наблюдении падающего тела невозможно заметить той первоначальной бесконечной (и даже не бесконечной, а хотя бы очень малой конечной) медленности, с которой тело движется в первые моменты падения. И вот Галилей предлагает для демонстрации другой случай: изменение давления падающего груза на сваю по мере изменения высоты падения, которое опять-таки (изменение давления) совершенно невозможно заметить, когда высота падения становится меньше определенной конечной величины. Значит, именно то, что нужно было продемонстрировать, как раз и не удалось, потому что нет таких точных инструментов, с помощью которых можно было бы измерять, на какую долю миллиметра больше свая вошла в землю, когда груз "падал" на нее с высоты, равной толщине листка, по сравнению со случаем, если бы он просто давил на нее без всякого падения.
Дальнейшее изложение Галилея показывает, что он рассуждает теоретически, и все его построение носит характер теоретического допущения, так называемого мысленного эксперимента, не могущего получить точного аналога в опыте, потому что никакой опыт и никакое измерение не могут иметь места там, где речь идет о бесконечно малой скорости. "...Нетрудно, - пишет Галилей, - установить ту же истину путем простого рассуждения. Предположим, что мы имеем тяжелый камень, поддерживаемый в воздухе в состоянии покоя; лишенный опоры и отпущенный на свободу, он начнет падать вниз, причем движение его будет не равномерным, но сначала медленным, а затем ускоряющимся. А так как скорость может увеличиваться и уменьшаться до бесконечности, то что может заставить меня признать, будто такое тело, выйдя из состояния бесконечной медленности (каковым именно является состояние покоя), сразу приобретает скорость в десять градусов скорее, чем в четыре, или в четыре градуса скорее, чем в два градуса, в один, в полградуса, в одну сотую градуса, словом, скорее, чем любую бесконечно малую скорость?"
В свое время Э. Мах охарактеризовал приведенные выше эксперименты Галилея как мысленные, или воображаемые. Нельзя не отметить, что на протяжении XVII- XVIII вв. проблема мысленного эксперимента и его статуса неоднократно становилась темой дискуссий. Характерен и другой эксперимент Галилея: движение тел по наклонной плоскости. Вот как описывает Галилей этот эксперимент, с помощью которого устанавливается закон свободного падения тел: "Вдоль узкой стороны линейки или, лучше сказать, деревянной доски, длиною около двенадцати локтей, шириною пол-локтя и толщиною около трех дюймов, был прорезан канал, шириною немного больше одного дюйма. Канал этот был прорезан совершенно прямым и, чтобы сделать его достаточно гладким и скользким, оклеен внутри возможно ровным и полированным пергаментом; по этому каналу мы заставляли падать гладкий шарик из твердейшей бронзы совершенно правильной формы. Установив изготовленную таким образом доску, мы поднимали конец ее над горизонтальной плоскостью, когда на один, когда на два локтя и заставляли скользить шарик по каналу... отмечая способом, о котором речь будет идти ниже, время, необходимое для пробега им всего пути; повторяя много раз один и тот же опыт, чтобы точно определить время, мы не находили никакой разницы даже на одну десятую времени биения пульса. Точно установив это обстоятельство, мы заставляли шарик проходить лишь четвертую часть длины того же канала; измерив время его падения, мы всегда находили самым точным образом, что оно равняется половине того, которое наблюдалось в первом случае". Галилей, как видим, больше всего озабочен точностью измерения: он подчеркивает совершенную прямизну прорезанного канала, его предельную гладкость, позволяющую свести сопротивление до минимума, чтобы уподобить движение по наклонной плоскости его "парадигме" - качанию маятника. Но важнее всего Галилею точное измерение времени падения шарика, которое призвано подтвердить закон, установленный Галилеем математически и гласящий, что отношение пройденных путей равно отношению квадратов времени их прохождения. О "совершенной точности" обычно не говорил почитаемый Галилеем Архимед, хотя его приборы служили образцом для подражания в XVII в. В чем тут различие?
2. Парадоксы теоретического мышления Галилея.
Мы не можем найти у Галилея систематически продуманной исследовательской программы именно потому, что почти все его важнейшие понятия содержат в себе противоречие.
Рассмотрим с этой точки зрения исходные понятия галилеевской механики и ее методологические принципы.
Начнем с понятия континуума. Здесь Галилей утверждает, что континуум состоит из неделимых, природа которых парадоксальна: они сами не имеют величины, но из их бесконечного множества составляется любая конечная величина. Тут одно непонятное - лишенная величины составная часть тела - объясняется через другое непонятное: актуально существующее бесконечное множество. Это понятие - парадокс получает название бесконечно малого и играет важную роль как в механике Галилея, так и в его математике. Сам Галилей не пришел к определенному и однозначному решению этого вопроса.
Однако с помощью этого самого противоречивого понятия "неделимого", или "бесконечно малого", Галилей вводит важную категорию механики - "мгновенную скорость", отменяя тем самым принципы аристотелевской теории движения. При обсуждении вопроса о бесконечной медленности, представляющей собой опять - таки совпадение противоположностей - покоя и движения, аристотелик Симпличио возражает против введения этого понятия, указывая на грозящий здесь парадокс Зенона: "Но если степени все большей и большей медленности бесчисленны, то они никогда не могут быть все исчерпаны. Таким образом, подымающийся камень никогда не пришел бы в состояние покоя, но пребывал бы в бесконечном, постоянно замедляющемся движении, чего, однако, в действительности никогда не бывает". На это Галилей дает ответ, формулируя ключевое понятие своей динамики - понятие мгновенной скорости: "Это случилось бы, синьор Симпличио, если бы тело двигалось с каждой степенью скорости некоторое определенное время; но оно только проходит через эти степени, не задерживаясь больше, чем на мгновение; а так как в каждом, даже в самом малом промежутке времени содержится бесконечное множество мгновений, то их число является достаточным для соответствия бесконечному множеству уменьшающихся степеней скорости". Галилей здесь опять-таки прибегает к понятию суммы бесконечно большого числа бесконечно малых отрезков времени, которым соответствует сумма бесконечно большого числа "мгновенных скоростей". Но что же такое "мгновенная скорость"? "Мгновенная скорость" - это уже не скорость в собственном смысле слова, ибо всякая скорость предполагает движение, а движение может происходить только во времени. Значит, мгновенная скорость - это нечто вроде неподвижного начала движения. По Галилею, всякая скорость складывается из бесконечной суммы мгновенных скоростей, и это обращение к бесконечной сумме представляет собой как бы магическое заклинание, с помощью которого совершается прыжок от вневременных мгновений к времени, от непространственных неделимых к пространству, от "неподвижных составляющих" движения к самому движению - одним словом, "переход в другой род". Средством этого перехода оказывается дифференциал, ибо именно дифференциалом и является "мгновенная скорость" у Галилея.
С помощью понятия "мгновенной скорости" Галилей решает проблему континуума. Средством решения, как видим, и здесь оказывается обращение к парадоксу, которое Галилей, хотя и не без колебаний, позволяет себе, но не терпит у других, например у своего ученика Кавальери. Через понятие бесконечно малого, которое, если говорить строго, не есть ни реальность математическая (по крайней мере, в смысле традиционной античной математики), ни реальность физическая, Галилей и осуществляет построение физики на основе математики.
Именно потому, что в понятии бесконечно малого с самого начала заложено противоречие, это противоречие с неизбежностью воспроизводится на каждом следующем этапе развития галилеевской мысли. Этим объясняется, почему Декарт не мог принять многих утверждений Галилея, в частности его тезиса о переходе падающего тела через все степени медленности. В 1639 г. в письме к Мерсенну Декарт замечает: "Следует знать, что бы ни говорили против этого Галилей и некоторые другие, что тела, начинающие падать или двигаться ...вовсе не проходят через все степени медленности, а имеют с первого момента определенную скорость, которая затем значительно возрастает".
Лейбниц высказывает в адрес Галилея упрек еще более серьезный, имея в виду уже не частный вопрос: он считает, что Галилей не развязал узел парадоксов континуума, а разрубил его. Этот упрек, несомненно, справедлив. Сам Лейбниц считал проблему континуума главной в натурфилософии и посвятил ее решению не меньше сил, чем в свое время Аристотель.
Принцип механики Галилея, таким образом, состоит в том, что он предложил приписывать вещи только то, что необходимо следует из вложенного в нее нами самими.
Галилео Галилеем был открыт принцип относительности движения. Так говорил Галилей о возможности постичь относительность движения: "Уединитесь под палубой большого корабля и пустите туда мух, бабочек и других подобных насекомых. Пусть там находится также большой сосуд с плавающими в нем рыбками. Подвесьте наверху ведерко, из которого капля за каплей вытекала бы вода, и погрузитесь в созерцание. При определенном везении с погодой, в процессе путешествия вы сможете постичь принцип относительности. Отличить равномерное прямолинейное движение такого корабля от покоя, находясь внутри, невозможно."
Глава 2. Механика И. Ньютона.
1. Вклад Ньютона в развитие естествознания.
Вершиной научного творчества И. Ньютона является его бессмертный труд “Математические начала натуральной философии”, впервые опубликованный в 1687 году. В нем он обобщил результаты, полученные его предшественниками и свои собственные исследования и создал впервые единую стройную систему земной и небесной механики, которая легла в основу всей классической физики. Здесь Ньютон дал определения исходных понятий – количества материи, эквивалентного массе, плотности; количества движения, эквивалентного импульсу, и различных видов силы. Формулируя понятие количества материи, он исходил из представления о том, что атомы состоят из некой единой первичной материи; плотность понимал как степень заполнения единицы объема тела первичной материей. На основе учение Ньютона о всемирном тяготении он разработал теорию движения планет, спутников и комет, образующих солнечную систему. Опираясь на этот закон, он объяснил явление приливов и сжатие Юпитера.
Концепция Ньютона явилась основой для многих технических достижений в течение длительного времени. На ее фундаменте сформировались многие методы научных исследований в различных областях естествознания.
Природа этой силы была открыта Исааком Ньютоном, работы которого завершили первую глобальную естественно-научную революцию. Он доказал существование тяготения как универсальной силы и сформулировал закон всемирного тяготения.
Ньютоновская физика стала вершиной развития взглядов в понимании мира природы в классической науке. Ньютон обосновал физико-математическое понимание природы, ставшее основой для всего последующего развития естествознания и формирования классического естествознания. В ходе своих исследований Ньютон создал методы дифференциального и интегрального исчисления для решения проблем механики. Благодаря этому ему удалось сформулировать основные законы динамики и закон всемирного тяготения. Механика Ньютона основана на понятиях количества материи (массы тела), количества движения, силы и трех законов движения: закона инерции, закона пропорциональности силы и ускорения и закона равенства действия и противодействия.
В своей механике Ньютон отказался от построения всеобъемлющей картины Вселенной и создал собственный метод физического исследования, который опирается на опыт, ограничивающийся фактами, и не претендует на познание всех конечных причин. Согласно ньютоновской концепции, физическая реальность характеризуется понятиями пространства, времени, материальной точки и силы (взаимодействия материальных точек). Любое физическое действие представляет собой движение материальных точек в пространстве, управляемое неизменными законами механики.
Хотя Ньютон громко провозгласил: «Гипотез не измышляю!», тем не менее некоторое количество гипотез было им предложено и они сыграли очень важную роль в развитии естествознания. Эти гипотезы были связаны с дальнейшей разработкой идеи всемирного тяготения, которое оставалось достаточно загадочным и непонятным. В частности, необходимо было ответить на вопросы: «Каков механизм действия этой силы?», «С какой скоростью она распространяется?», «Есть ли у нее материальный носитель?».
Работы Ньютона завершили первую глобальную научную революцию, сформировав классическую полицентрическую научную картину мира и заложив фундамент классической науки Нового времени.
2. Первый закон Ньютона.
Закон инерции впервые был установлен Галилеем для случая горизонтального движения: когда тело движется по горизонтальной плоскости, то его движение является равномерным и продолжалось бы постоянно, если бы плоскость простиралась в пространстве без конца. Ньютон дал более общую формулировку закону инерции как первому закону движения: всякое тело пребывает в состоянии покоя или равномерного прямолинейного движения до тех пор, пока действующие на него силы не изменят это состояние.
В жизни этот закон описывает случай когда, если перестать тянуть или толкать движущееся тело, то оно останавливается, а не продолжает двигаться с постоянной скоростью. Так автомобиль с выключенным двигателем останавливается. По закону Ньютона на катящийся по инерции автомобиль должна действовать тормозящая сила, которой на практике является сопротивление воздуха и трение автомобильных шин о поверхность шоссе. Они-то и сообщают автомобилю отрицательное ускорение до тех пор, пока он не остановиться.
Недостатком данной формулировки закона является то, что в ней не содержалось указания на необходимость отнесения движения к инерциальной системе координат. Дело в том, что Ньютон не пользовался понятием инерциальной системы координат, – вместо этого он вводил понятие абсолютного пространства – однородного и неподвижного, – с которым и связывал некую абсолютную систему координат, относительно которой и определялась скорость тела. Когда бессодержательность абсолютного пространства как абсолютной системы отсчета была выявлена, закон инерции стал формулироваться иначе: относительно инерциальной системы координат свободное тело сохраняет состояние покоя или равномерного прямолинейного движения.
3. Второй закон Ньютона.
В формулировке второго закона Ньютон ввел понятия:
Ускорение a – векторная величина (Ньютон называл его количеством движения и учитывал при формулировании правила параллелограмма скоростей), определяющая быстроту изменения скорости движения тела.
Сила F – векторная величина, понимаемая как мера механического воздействия на тело со стороны других тел или полей, в результате воздействия которой тело приобретает ускорение или изменяет свою форму и размеры.
Масса тела m – физическая величина – одна из основных характеристик материи, определяющая ее инерционные и гравитационные свойства.
Второй закон механики
гласит: сила, действующая на тело, равна произведению массы тела на сообщаемое
этой силой ускорение. Такова его современная формулировка. Ньютон сформулировал
его иначе: изменение количества движения пропорционально приложенной
действующей силе и происходит по направлению той прямой, по которой эта сила
действует, и обратно пропорционально массе тела или математически: 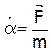
 На опыте этот закон легко
подтвердить, если к концу пружины прикрепить тележку и отпустить пружину, то за
время t тележка пройдет путь S1 (рис.
1), затем к той же самой пружине прикрепить две тележки, т.е. увеличить массу
тела в два раза, и отпустить пружину, то за то же время t они
пройдут путь S2, в два раза меньший, чем S1.
На опыте этот закон легко
подтвердить, если к концу пружины прикрепить тележку и отпустить пружину, то за
время t тележка пройдет путь S1 (рис.
1), затем к той же самой пружине прикрепить две тележки, т.е. увеличить массу
тела в два раза, и отпустить пружину, то за то же время t они
пройдут путь S2, в два раза меньший, чем S1.
4. Третий закон Ньютона
Третий закон Ньютона гласит: действию всегда есть равное и противоположное противодействие, иначе тела действуют друг на друга с силами, направленными вдоль одной прямой, равными по модулю и противоположными по направлению или математически:
 Ньютон распространил действие этого
закона на случай и столкновения тел, и на случай их взаимного притяжения.
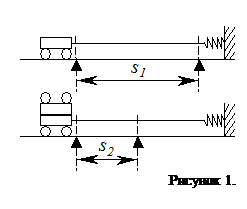
Простейшей демонстрацией этого закона может служить тело, расположенное на
горизонтальной плоскости, на которое действуют сила тяжести Fт
и сила реакции опоры Fо, лежащие на одной прямой,
равные по значению и противоположно направленные, равенство этих сил позволяет
телу находиться в состоянии покоя (рис. 2).
Ньютон распространил действие этого
закона на случай и столкновения тел, и на случай их взаимного притяжения.
Простейшей демонстрацией этого закона может служить тело, расположенное на
горизонтальной плоскости, на которое действуют сила тяжести Fт
и сила реакции опоры Fо, лежащие на одной прямой,
равные по значению и противоположно направленные, равенство этих сил позволяет
телу находиться в состоянии покоя (рис. 2).
5. Фундаментальные законы движения Ньютона
Если кинематика изучает движение геометрического тела, который не обладает никакими свойствами материального тела, кроме свойства занимать определенное место в пространстве и изменять это положение с течением времени, то динамика изучает движение реальных тел под действием приложенных к ним сил. Установленные Ньютоном три закона механики лежат в основе динамики и составляют основной раздел классической механики.
Непосредственно их можно применять к простейшему случаю движения, когда движущееся тело рассматривается как материальная точка, т.е. когда размер и форма тела не учитывается и когда движение тела рассматривается как движение точки, обладающей массой. Для описания движения точки можно выбрать любую систему координат, относительно которой определяются характеризующие это движение величины. За тело отсчета может быть принято любое тело, движущееся относительно других тел. В динамике имеют дело с инерциальными системами координат, характеризуемыми тем, что относительно них свободная материальная точка движется с постоянной скоростью.
Из трех фундаментальных законов движения Ньютона вытекают следствия, одно из которых – сложение количества движения по правилу параллелограмма. Ускорение тела зависит от величин, характеризующих действие других тел на данное тело, а также от величин, определяющих особенности этого тела. Механическое действие на тело со стороны других тел, которое изменяет скорость движения данного тела, называют силой. Она может иметь разную природу (сила тяжести, сила упругости и т.д.). Изменение скорости движения тела зависит не от природы сил, а от их величины. Поскольку скорость и сила – векторы, то действие нескольких сил складывается по правилу параллелограмма. Свойство тела, от которого зависит приобретаемое им ускорение, есть инерция, измеряемая массой. В классической механике, имеющей дело со скоростями, значительно меньшими скорости света, масса является характеристикой самого тела, не зависящей от того, движется оно или нет. Масса тела в классической механике не зависит и от взаимодействия тела с другими телами. Это свойство массы побудило Ньютона принять массу за меру материи и считать, что величина ее определяет количество материи в теле. Таким образом, масса стала пониматься как количество материи.
Количество материи доступно измерению, будучи пропорциональным, весу тела. Вес–это сила, с которой тело действует на опору, препятствующую его свободному падению. Численно вес равен произведению массы тела на ускорение силы тяжести. Вследствие сжатия Земли и ее суточного вращения вес тела изменяется с широтой и на экваторе на 0,5% меньше, чем на полюсах. Поскольку масса и вес строго пропорциональны, оказалось возможным практическое измерение массы или количества материи. Понимание того, что вес является переменным воздействием на тело, побудило Ньютона установить и внутреннюю характеристику тела – инерцию, которую он рассматривал, как присущую телу способность сохранять равномерное прямолинейное движение, пропорциональную массе. Массу как меру инерции можно измерять с помощью весов, как это делал Ньютон.
В состоянии невесомости массу можно измерять по инерции. Измерение по инерции является общим способом измерения массы. Но инерция и вес являются различными физическими понятиями. Их пропорциональность друг другу весьма удобна в практическом отношении – для измерения массы с помощью весов. Таким образом, установление понятий силы и массы, а также способа их измерения позволило Ньютону сформулировать второй закон механики.
Первый и второй законы механики относятся соответственно к движению материальной точки или одного тела. При этом учитывается лишь действие других тел на данное тело. Однако всякое действие есть взаимодействие. Поскольку в механике действие характеризуется силой, то если одно тело действует на другое с определенной силой, то второе действует на первое с той же силой, что и фиксирует третий закон механики. В формулировке Ньютона третий закон механики справедлив лишь для случая непосредственного взаимодействия сил или при мгновенной передаче действия одного тела на другое. В случае передачи действия за конечный промежуток времени данный закон применяется тогда, когда временем передачи действия можно пренебречь.
Уравнение F=ma (то есть второй закон Ньютона) является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости. Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.
Изучение Фундаментальных законов физики подтверждает, что наука поступательно развивается: каждый этап, каждый открытый закон является этапом в развитии, но не даёт окончательных ответов на все вопросы.
6. Закон всемирного тяготения.
Считается, что стержнем динамики Ньютона является понятие силы, а основная задача динамики заключается в установлении закона из данного движения и, наоборот, в определении закона движения тел по данной силе. Из законов Кеплера Ньютон вывел существование силы, направленной к Солнцу, которая была обратно пропорциональна квадрату расстояния планет от Солнца. Обобщив идеи, высказанные Кеплером, Гюйгенсом, Декартом, Борелли, Гуком, Ньютон придал им точную форму математического закона, в соответствии с которым утверждалось существование в природе силы всемирного тяготения, обусловливающей притяжение тел. Сила тяготения прямо пропорциональна произведению масс тяготеющих тел и обратно пропорционально квадрату расстояния между ними или математически:
, где G – гравитационная постоянная.
Данный закон описывает взаимодействие любых тел – важно лишь то, чтобы расстояние между телами было достаточно велико по сравнению с их размерами, это позволяет принимать тела за материальные точки. В ньютоновской теории тяготения принимается, что сила тяготения передается от одного тяготеющего тела к другому мгновенно, при чем без посредства каких бы то ни было сред. Закон всемирного тяготения вызвал продолжительные и яростные дискуссии. Это не было случайно, поскольку этот закон имел важное философское значение. Суть заключалась в том, что до Ньютона целью создания физических теорий было выявление и представление механизма физических явлений во всех его деталях. В тех случаях, когда это сделать не удавалось, выдвигался аргумент о так называемых "скрытых качествах", которые не поддаются детальной интерпретации. Бэкон и Декарт ссылки на "скрытые качества" объявили ненаучными. Декарт считал, что понять суть явления природы можно лишь в том случае, если его наглядно представить себе. Так, явления тяготения он представлял с помощью эфирных вихрей. В условиях широкого распространения подобных представлений закон всемирного тяготения Ньютона, несмотря на то, что демонстрировал соответствие произведенных на его основе астрономическим наблюдениям с небывалой ранее точностью, подвергался сомнению на том основании, что взаимное притяжение тел очень напоминало перипатетическое учение о "скрытых качествах". И хотя Ньютон установил факт его существования на основе математического анализа и экспериментальных данных, математический анализ еще не вошел прочно в сознание исследователей в качестве достаточно надежного метода. Но стремление ограничивать физическое исследование фактами, не претендующими на абсолютную истину, позволило Ньютону завершить формирование физики как самостоятельной науки и отделить ее от натурфилософии с ее претензиями на абсолютное знание.
В законе всемирного тяготения наука получила образец закона природы как абсолютно точного, повсюду применимого правила, без исключений, с точно определенными следствиями. Этот закон был включен Кантом в его философию, где природа представлялась царством необходимости в противоположность морали - царству свободы.
Физическая концепция Ньютона была своеобразным венцом физики XVII века. Статический подход к Вселенной был заменен динамическим. Эксперементально-математический метод исследования, позволив решить многие проблемы физики XVII века, оказался пригодным для решения физических проблем еще в течение двух веков.
7. Законы Кеплера.
Наиболее простой задачей небесной механики является гравитационное взаимодействие двух тел в пустом пространстве. Эта задача решается аналитически до конца; результат её решения часто формулируют в виде трёх законов Кеплера.
При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении, достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе, эта неустойчивость не позволяет предсказать движение планет на масштабах, превышающих сотню миллионов лет.
В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений, и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — нетривиальная структура колец Сатурна.
Несмотря на попытки описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.
В сильных гравитационных полях, при движении с релятивистскими скоростями, начинают проявляться эффекты общей теории относительности:
¾ отклонение закона тяготения от ньютоновского;
¾ запаздывание потенциалов, связанное с конечной скоростью распространения гравитационных возмущений; появление гравитационных волн;
¾ эффекты нелинейности: гравитационные волны имеют свойство взаимодействовать друг с другом, поэтому принцип суперпозиции волн в сильных полях уже не выполняется;
¾ изменение геометрии пространства-времени;
¾ возникновение черных дыр;
Существует современная каноническая классическая теория гравитации — общая теория относительности, и множество уточняющих её гипотез и теорий различной степени разработанности, конкурирующих между собой. Все эти теории дают очень похожие предсказания в рамках того приближения, в котором в настоящее время осуществляются экспериментальные тесты. Далее описаны несколько основных, наиболее хорошо разработанных или известных теорий гравитации.
Теория гравитации Ньютона основана на понятии силы тяготения, которая является дальнодействующей силой: она действует мгновенно на любом расстоянии. Этот мгновенный характер действия несовместим с полевой парадигмой современной физики и, в частности, со специальной теорией относительности, созданной в 1905 году Эйнштейном, вдохновлённым работами Пуанкаре и Лоренца. В теории Эйнштейна никакая информация не может распространиться быстрее скорости света в вакууме. Математически сила гравитации Ньютона выводится из потенциальной энергии тела в гравитационном поле. Потенциал гравитации, соответствующий этой потенциальной энергии, подчиняется уравнению Пуассона, которое не инвариантно при преобразованиях Лоренца. Причина неинвариантности заключается в том, что энергия в специальной теории относительности не является скалярной величиной, а переходит во временну́ю компоненту 4-вектора. Векторная же теория гравитации оказывается аналогичной теории электромагнитного поля Максвелла и приводит к отрицательной энергии гравитационных волн, что связано с характером взаимодействия: одноимённые заряды (массы) в гравитации притягиваются, а не отталкиваются, как в электромагнетизме.Таким образом, теория гравитации Ньютона несовместима с фундаментальным принципом специальной теории относительности — инвариантностью законов природы в любой инерциальной системе отсчёта, а прямое векторное обобщение теории Ньютона, впервые предложенное Пуанкаре в 1905 году в его работе “О динамике электрона”, приводит к физически неудовлетворительным результатам.
Эйнштейн начал поиск теории гравитации, которая была бы совместима с принципом инвариантности законов природы относительно любой системы отсчёта. Результатом этого поиска явилась общая теория относительности, основанная на принципе тождественности гравитационной и инертной массы.
В классической механике Ньютона существует два понятия массы: первое относится ко второму закону Ньютона, а второе — к закону всемирного тяготения. Первая масса — инертная (или инерционная) — есть отношение негравитационной силы, действующей на тело, к его ускорению. Вторая масса — гравитационная (или, как её иногда называют, тяжёлая) — определяет силу притяжения тела другими телами и его собственную силу притяжения. Вообще говоря, эти две массы измеряются, как видно из описания, в различных экспериментах, поэтому совершенно не обязаны быть пропорциональными друг другу. Их строгая пропорциональность позволяет говорить о единой массе тела как в негравитационных, так и в гравитационных взаимодействиях. Подходящим выбором единиц можно сделать эти массы равными друг другу.
Сам принцип был выдвинут ещё Исааком Ньютоном, а равенство масс было проверено им экспериментально с относительной точностью 10−3. В конце XIX века более тонкие эксперименты провёл Этвёш, доведя точность проверки принципа до 10−9. В течение XX века экспериментальная техника позволила подтвердить равенство масс с относительной точностью 10−12—10−13 (Брагинский, Дикке и т. д.).
Принцип движения по геодезическим линиям. Если гравитационная масса точно равна инерционной, то в выражении для ускорения тела, на которое действуют лишь гравитационные силы, обе массы сокращаются. Поэтому ускорение тела, а следовательно, и его траектория не зависит от массы и внутреннего строения тела. Если же все тела в одной и той же точке пространства получают одинаковое ускорение, то это ускорение можно связать не со свойствами тел, а со свойствами самого пространства в этой точке.Таким образом, описание гравитационного взаимодействия между телами можно свести к описанию пространства-времени, в котором двигаются тела. Естественно предположить, как это и сделал Эйнштейн, что тела двигаются по инерции, то есть так, что их ускорение в собственной системе отсчёта равно нулю. Траектории тел тогда будут геодезическими линиями, теория которых была разработана математиками ещё в XIX веке.
Сами геодезические линии можно найти, если задать в пространстве-времени аналог расстояния между двумя событиями, называемый по традиции интервалом или мировой функцией. Интервал в трёхмерном пространстве и одномерном времени (иными словами, в четырёхмерном пространстве-времени) задаётся 10 независимыми компонентами метрического тензора. Эти 10 чисел образуют метрику пространства. Она определяет “расстояние” между двумя бесконечно близкими точками пространства-времени в различных направлениях. Геодезические линии, соответствующие мировым линиям физических тел, скорость которых меньше скорости света, оказываются линиями наибольшего собственного времени, то есть времени, измеряемого часами, жёстко скреплёнными с телом, следующим по этой траектории.
Современные эксперименты подтверждают движение тел по геодезическим линиям с той же точностью, как и равенство гравитационной и инертной масс.
8. Границы применимости механики Ньютона.
Результатом развития классической механики явилось создание единой механической картины мира, в рамках которой все качественное многообразие мира объяснялось различиями в движении тел, подчиняющемся законам ньютоновской механики. Согласно механической картине мира, если физическое явление мира можно было объяснить на основе законов механики, то такое объяснение признавалось научным. Механика Ньютона, таким образом, стала основой механической картины мира, господствовавшей вплоть до научной революции на рубеже XIX и XX столетий.
 Механика Ньютона, в отличие от
предшествующих механических концепций, давала возможность решать задачу о любой
стадии движения, как предшествующей, так и последующей, и в любой точке
пространства при известных фактах, обусловливающих это движение, а также
обратную задачу определения величины и направления действия этих факторов в
любой точке при известных основных элементах движения. Благодаря этому механика
Ньютона могла использоваться в качестве метода количественного анализа
механического движения. Любые физические явления могли изучаться как,
независимо от вызывающих их факторов.
Механика Ньютона, в отличие от
предшествующих механических концепций, давала возможность решать задачу о любой
стадии движения, как предшествующей, так и последующей, и в любой точке
пространства при известных фактах, обусловливающих это движение, а также
обратную задачу определения величины и направления действия этих факторов в
любой точке при известных основных элементах движения. Благодаря этому механика
Ньютона могла использоваться в качестве метода количественного анализа
механического движения. Любые физические явления могли изучаться как,
независимо от вызывающих их факторов.
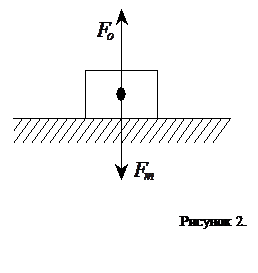
Например, можно вычислить скорость спутника Земли: Для простоты найдем скорость спутника υсп с орбитой, равной радиусу Земли (рис. 3). С достаточной точностью можно приравнять ускорение спутника ускорению свободного падения на поверхности Земли: .
С другой стороны центростремительное ускорение спутника
Поэтому , откуда ![]() – Эта скорость называется первой
космической скоростью. Тело любой массы, которому будет сообщена такая
скорость, станет спутником Земли.
– Эта скорость называется первой
космической скоростью. Тело любой массы, которому будет сообщена такая
скорость, станет спутником Земли.
Законы ньютоновской механики связывали силу не с движением, а с изменением движения. Установив динамический взгляд на мир вместо традиционного статического, Ньютон свою динамику сделал основой теоретической физики. Хотя Ньютон проявлял осторожность в механических истолкованиях природных явлений, все равно считал желательным выведение из начал механики остальных явлений природы. Дальнейшее развитие физики стало осуществляться в направлении дальнейшей разработки аппарата механики применительно к решению конкретных задач, по мере решения которых механическая картина мира укреплялась. Вследствие развития физики в начале XX века определилась область применения классической механики: ее законы выполняются для движений, скорость которых много меньше скорости света. Было установлено, что с ростом скорости масса тела возрастает. Вообще законы классической механики Ньютона справедливы для случая инерциальных систем отсчета. В случае неинерциальных систем отсчета ситуация иная. При ускоренном движении неинерциальной системы координат относительно инерциальной системы первый закон Ньютона (закон инерции) в этой системе не имеет места, – свободные тела в ней будут с течением времени менять свою скорость движения.
Первое несоответствие в классической механике было выявлено, тогда когда был открыт микромир. В классической механике перемещения в пространстве и определение скорости изучались вне зависимости от того, каким образом эти перемещения реализовывались. Применительно к явлениям микромира подобная ситуация, как выявилось, невозможна принципиально. Здесь пространственно-временная локализациявозможна лишь для некоторых частных случаев, которые зависят от конкретных динамических условий движения. В макро масштабах использование кинематики вполне допустимо. Для микро масштабов изучение движения вне зависимости от динамических условий, теряет смысл.
Для масштабов микромира и второй закон Ньютона оказался несостоятельным – он справедлив лишь для явлений большого масштаба. Выявилось, что попытки измерить какую-либо величину, характеризующую изучаемую систему, влечет за собой неконтролируемое изменение других величин, характеризующих данную систему: если предпринимается попытка установить положение в пространстве и времени, то это приводит к неконтролируемому изменению соответствующей сопряженной величины, которая определяет динамическое состояние системы. Так, невозможно точно измерить в одно и то же время две взаимно сопряженные величины. Чем точнее определяется значение одной величины, характеризующей систему, тем более неопределенным оказывается значение сопряженной ей величины. Это обстоятельство повлекло за собой существенное изменение взглядов на понимание природы вещей.
Несоответствие в классической механики исходило из того, что будущее в известном смысле полностью содержится в настоящем – этим и определяется возможность точного предвидения поведения системы в любой будущий момент времени. Такая возможность предлагает одновременное определение взаимно сопряженных величин. В области микромира это оказалось невозможным, что и вносит существенные изменения в понимание возможностей предвидения и взаимосвязи явлений природы: раз значение величин, характеризующих состояние системы в определенный момент времени, можно установить лишь с долей неопределенности, то исключается возможность точного предсказания значений этих величин в последующие моменты времени, т.е. можно лишь предсказать вероятность получения тех или иных величин.
Глава 3. Бэкон и Декарт.
1. Френсис Бэкон (1561—1626).
К началу XVII столетия была подготовлена почва для быстрого развития физики. Преподающаяся в университетах физика не в состоянии была дать объяснение новым явлениям, обнаруженным в результате технических и географических открытий. Обращение к наследию античной науки позволило исправить ряд заблуждений и восстановить в правах утраченные достижения, но этого было далеко не достаточно для дальнейшего движения вперед. Нельзя было пойти дальше, не сломив слепое преклонение перед Аристотелем, царившее в университетах. Коперник, Бруно, Галилей вынуждены были каждый по-своему вступить в борьбу с аристотелевской традицией. Это дело продолжали их современники и преемники.
Одним из современников Галилея, который особенно ясно осознал противоречие старой науки новым открытиям и необходимость опоры на новую методологию, был английский государственный деятель и философ Френсис Бэкон (1561—1626).
Бэкон разделяет ученых своего времени на два класса: эмпириков и догматиков. Эмпирики, подобно муравьям, тащат в свою муравьиную кучу всевозможные факты, догматики же, подобно пауку, ткут ткань из самих себя. Надо, по Бэкону, в науке работать как пчела; извлекать материал из внешнего мира и перерабатывать его рационально.
В основе метода Бэкона лежит опыт. Наука должна опираться на опыт, на практику, строя из них выводы, «причины и аксиомы» методом индукции (наведения), т. е. переходя от частных фактов к обобщениям. Эти обобщения вновь проверяются опытом и практикой. «Наш путь и наш метод... состоит в следующем: мы извлекаем не практику из практики и опыт из опытов (как эмпирики), а причины и аксиомы из практики и опытов и из причин и аксиом — снова практику и опыты, как верные истолкователи природы». Научные истины проверяются, таким образом, опытом и практикой и, в свою очередь, выводятся из них.
Существенно, что Бэкон хорошо понимал необходимость финансирования науки и организации научных учреждений. В своем неоконченном фантастическом произведении «Новая Атлантида» он описывает такое учреждение — «Дом Соломона» — и его огромное значение для рационально построенного общества.
Флорентийские академики (их было всего девять) совместно ставили и обсуждали опыты, описанные позднее в сборнике трудов академии, вышедшем в 1667 г. В этом же году покровитель академии брат герцога Тосканского Леопольд Медичи по требованию папских кругов вынужден был закрыть академию. Так церковь уничтожила наследие Галилея, нанеся тем самым огромный вред итальянской науке, уступившей лидерство в научном соревновании другим странам.
Еще раньше, чем во Флоренции, начиная с 1645 г., в Лондоне стал собираться кружок любителей естественных наук. В Англии в те годы бушевала гражданская война, участники кружка по мере развития революционных событий разделились: одни остались в Лондоне, другие собирались в Оксфорде. После реставрации кружок вновь начал собираться в Лондоне и оформился организационно, получив формальный королевский статут 28 ноября 1660 г. как Лондонское Королевское общество. Общество было основано «для преуспеяния экспериментальной философии» под девизом «ничего на слово» и существует и поныне как высшее научное учреждение Англии (Английская Академия наук).
Аналогичные собрания в сороковых годах проходили в Париже. Позднее министр короля Людовика XIV Кольбер внес предложение об открытии Академии наук в Париже, которая и была утверждена в 1666 г. Затем последовали организации научных обществ и академий в других государствах. Петр I во время своего путешествия по Европе знакомился с английским королевским обществом, президентом которого в то время был Ньютон. Уже будучи императором, Петр I посетил Париж и Парижскую Академию наук. Он хорошо понимал необходимость создания в России высшего научного учреждения. Он вел длительные переговоры с учеными Европы об организации академии и 28 января 1724 г. подписал указ об учреждении Петербургской Академии наук. Она начала свою работу в 1725 г., уже после смерти Петра, когда в Петербург приехали первые академики.
Таким образом, мы можем говорить о происшедшей в XVII в. научной революции, в результате которой возникла классическая физика (и не только физика) в той форме и с теми методами познания, какой мы ее сегодня знаем. Говоря о методе познания, следует напомнить, что наряду с индуктивным в современной науке находит широкое применение дедуктивный метод, когда из небольшого числа общих принципов выводятся и прослеживаются в деталях частные следствия. Так, классическая механика развивается из законов Ньютона или из вариационных принципов динамики, макроскопическая электродинамика — из уравнений Максвелла и т. д. Метод дедукции был обоснован вскоре после Бэкона французским философом Рене Декартом (1596—1650) в книге «Рассуждение о методе», которая вышла в свет в 1637 г.
Следует, однако, подчеркнуть, что было бы грубым упрощением считать Декарта основателем дедуктивного метода, а Бэкона—основателем индуктивного. Оба метода зародились еще в Древней Греции, и Бэкон и Декарт лишь развили их применительно к естествознанию. При этом ни Бэкон не отрицал значения дедукции, ни Декарт не отрицал значения опыта и индукции. Но Бэкон подчеркивал ведущую роль опыта и индукции, Декарт же — логического анализа и правильных умозаключений. Он полагал, что в основу этих умозаключений должны был положены ясные и простые принципы и строгая логическая последовательность выводов. Математика в методе Декарта играет первостепенную роль.
2. 'Начала философии' Рене Декарта.
Но основной проблемой физики XVII в. были законы движения. Как применить математику к движению? И здесь Декарту принадлежит решающее открытие: он ввел в математику переменные величины, установил соответствие между геометрическими образами и алгебраическими уравнениями; Декарт положил начало аналитической геометрии. Здесь он «первые применил свой метод: «Приняв во внимание, что среди всех, искавших истину в науках, только математикам удалось найти некоторые доказательства, т.е. некоторые точные и очевидные соображения, я не сомневался, что и мне следовало начать с того, что было ими обследовано» Результатом такого начала явилась «геометрия», приложенная к «Рассуждению о методе». Другими приложениями являются «Диоптрика» и «Метеоры». Р. Декарт впервые после Левкиппа разработал вариант материалистической космогонии - учения о возникновении Вселенной и изложил ее в виде вымысла «фаблио».
Известны три закона Декарта в механике: два закона инерции, причем вслед за Галилеем, но абсолютно точно, с указанием на прямолинейность инерционного движения формулирует 1-й закон Ньютона и закон постоянства количества движения - закон сохранения импульса, впрочем еще не в векторной форме и без четкого различия упругого и неупругого удара.
Декарт был одним из тех, кто создавал в XVII в. новое понятие науки - универсальной механики, которая царила вплоть до конца XVIII века, времени открытия тепловых, магнитных и электрических явлений. Даже те, кто были противниками континуалистской концепции (атомисты) и те, в конце концов, пользовались языком механической науки, созданной Декартом.
Требование простоты и ясности - основной принцип его методологии. Простота математических принципов играет первостепенную роль. В установлении исходных принципов и их проверке важную роль играет опыт.
Свой метод Декарт формулирует в виде четырех правил:
1. «Никогда не принимать за истинное ничего, что не познал бы таковым с очевидностью, иначе говоря, тщательно избегая опрометчивости и предвзятости и включать в свои суждения только то, что представляется моему уму столь ясно и столь отчетливо, что не дает мне никакого повода подвергать их сомнению». Итак, начинать надо с простого и очевидного.
2. «Делить каждое из исследуемых мною затруднений на столько частей, сколько это возможно и нужно для лучшего их преодоления.». Принцип анализа, разъятия явления на составные части, упрощения-редукционизма.
3. Поддерживаться определенного порядка мышления, начиная с предметов наиболее простых и наиболее легко познаваемых и восходя постепенно к познанию наиболее сложного, предполагая порядок даже «там, где объекты мышления вовсе не даны в их естественной связи». Другими словами, из простого и очевидного путем дедукции получать более сложное.
4. Составлять всегда перечни столь полные и обзоры столь общие, чтобы была уверенность в отсутствии упущений. Действовать так, чтобы не было упущено ни единого звена, то есть сохранение непрерывной цепи заключений.
В 1644 г Декарт издал обширное сочинение под названием «Начала философии» В него вошли части сочинения Декарта о мире (космосе), которое он намеревался издать еще в 1633 г. Услышав об осуждении Галилея, он отложил издание своего сочинения и только спустя одиннадцать лет обнародовал его в расширенном и переработанном виде. В этом сочинении он изложил грандиозную программу создания теории природы, руководствуясь своим методологическим правилом брать за основу наиболее простые и ясные положения. Еще в «Рассуждении о методе» Декарт подверг анализу всевозможные исходные положения, сомневаясь в справедливости любого из них, в том числе и в положении «Я существую» Однако в акте мышления сомнение невозможно, ибо наше сомнение уже есть мысль. Отсюда знаменитое положение Декарта «Я мыслю, следовательно, существую».
Материя Декарта — это чистая протяженность, материальное пространство, заполняющее всю безмерную длину, ширину и глубину Вселенной Части материи находятся в непрерывном движении, взаимодействуя друг с другом при контакте
В отличие от Галилея Декарт отвлекается от действия тяготения, которое он, между прочим, также сводит к движению и взаимодействию частиц, и упоминает о направлении инерционного движения по прямой. Однако его формулировка еще отличается от ньютоновской, он говорит не о состоянии равномерного и прямолинейного движения, а вообще о состоянии, не разъясняя подробно содержания его термина.
Из всего содержания «Начал» вид но, что состояние частей материи характеризуется их величиной («количество материи»), формой, скоростью движения и способностью изменять эту скорость под воздействием внешних частиц Можно отождествить эту способность с инерцией, и тогда в одном из писем Декарта мы встречаем очень интересное утверждение «Можно утверждать с достоверностью, что камень неодинаково расположен к принятию нового движения или к увеличению скорости, когда он движется очень скоро и когда он движется очень медленно». Другими словами: Декарт утверждает, что инерция тела зависит от его скорости. В письмах Декарта встречается формулировка закона инерции, уже почти текстуально совпадающая с ньютоновской: «Полагаю, что природа движения такова, что, если тело пришло в движение, уже этого достаточно, чтобы оно его продолжало с той же скоростью и в направлении той же прямой линии, пока оно не будет остановлено или отклонено какой-либо другой причиной».
Этот принцип сохранения скорости по модулю и направлению тем более интересен у Декарта, что, по его представлению, пустоты в мире нет и всякое движение является циклическим: одна часть материи занимает место другой, эта — предыдущей и т. д. В результате вся Вселенная пронизана вихревыми движениями материи. Движение во Вселенной вечно, так же как и сама материя (хотя Декарт и пишет о сотворении материи и движения богом, но в дальнейшем бог устраняется и природа действует по собственным законам), и все явления в мире сводятся к движениям частиц материи. В начале эти движения были хаотическими и беспорядочными, в результате этих движений частицы дробились и сортировались
По Декарту, существуют три сорта частиц (три элемента): частицы земли, воздуха (неба), огня. Наиболее крупные частицы— это частицы земли. Они погружены в среду из частиц неба, в которые вкраплены также частицы огня, образующие Солнце. Вихревые движения круглых подвижных частиц «неба» увлекают в своем движении планеты, состоящие из элементов земли. Вся Вселенная разбита на такие вихревые области, которые можно рассматривать как предшественники современных галактик. Такова космогоническая гипотеза Декарта.
В физике Декарта нет места силам, тем более силам, действующим на расстоянии через пустоту. Все явления мира сводятся к движениям и взаимодействию соприкасающихся частиц. Такое физическое воззрение получило в истории науки название картезианского, от латинского произношения имени Декарта — Картезий. Все попытки построить единую теорию поля и вещества по существу повторяют на новой основе попытку Декарта построить физическую картину мира с непрерывной материей и сохраняющимся механическим движением.
Механика Декарта представляет собой дальнейшее развитие идей А.Эйнштейна по геометризации всех физических полей и взаимодействий, включая механические взаимодействия. Нам всегда казалось, что механика далека от современной теории поля, поскольку в большинстве случаев описывает динамику макрообъектов, движущихся с малыми скоростями под действием внешних сил. И это утверждение справедливо до тех пор, пока мы имеем дело с малыми ускорениями. При больших ускорениях в механических процессах (да и в теории поля тоже) существенную роль начинают играть поля и силы инерции, значение и смыл которых современная наука либо игнорирует, либо воспринимает слишком формально. Вот что пишет по этому поводу А.Пайс в книге «Научная деятельность и жизнь Альберта Эйнштейна», Москва, Наука, 1989: «По моему мнению, проблема происхождения инерции была и остается наиболее темным вопросом в теории частиц и полей».
В механике Декарта проблему инерции удалось связать с кручением Риччи и кривизной Римана пространства событий. Рассуждения в данном случае весьма просты: если всякое движение есть вращение, а вращение порождает силы и поля инерции, то любое движение не может быть понято на достаточно глубоком уровне без основательного развития теории полей инерции. Таким образом, механика оказывается связанной с теорией поля.
Надо отметить, что проблема инерции интересует физиков со времен Ньютона. Почему искривляется поверхность воды в ведре при его вращении? Чтобы объяснить этот опытный факт Ньютон вводит в физику понятие абсолютного пространства (эфир Ньютона) и трактует появление сил инерции, искривляющих поверхность воды во вращающемся ведре, ускоренным движением ведра относительно абсолютного пространства. Ньютон связывает с абсолютным пространством инерциальную систему отсчета, которая в механике Ньютона играет определяющую роль.
3. Пространство и время. Специальная теория относительности
Учение Декарта и направление в философии и естествознании, продолжавшее его идеи, получило название картезианства - от латинизированной формы имени Декарт. Он оказал значительное влияние на последующее развитие науки и философии, причём как идеализма, так и материализма. Учения Декарта о непосредственной достоверности самосознания, о врождённых идеях, об интуитивном характере аксиом, о противоположности материального и идеального явились опорой для развития идеализма. С другой стороны, учение Декарта о природе и его всеобщий механистический метод делают философию Декарта одним из этапов материалистического мировоззрения нового времени.Пространство и время как всеобщие и необходимые формы бытия материи являются фундаментальными категориями в современной физике и других науках. Ньютоновская концепция пространства и времени оказалась господствующей вплоть до конца ХIХ в. Основные положения ее заключаются в следующем: Пространство считалось бесконечным, плоским, прямолинейным. Оно рассматривалось как абсолютное, пустое, однородное и изотропное (нет выделенных точек и направлений) и выступало в качестве вместилища материальных тел, как независимая инерциальная система.
Время понималось абсолютным, однородным, равномерным текущим. Оно идет сразу и везде во всей Вселенной, единообразно и синхронно и выступает как независимый от материальных объектов процесс длительности.
Абсолютное время и пространство служили основой для преобразований Галилея – Ньютона, посредством которых осуществлялся переход к инерциальным системам. До ХIХ в. физика была в основном физикой вещества, но изучение электродинамики, оптики выявило недостаточность одной классической механики для полного описания явлений природы. Специальная теория относительности, созданная в 1905 г. А.Эйнштейном, стала результатом обобщения и синтеза классической механики Галилея - Ньютона и электродинамики Максвелла-Лоренца.
Она описывает законы всех физических процессов при скоростях движения, близких к скорости света, но без учета поля тяготения. При уменьшении скоростей движения она сводится к классической механике, которая, таким образом оказывается ее частным случаем.
Для всех физических процессов скорость света обладает свойством бесконечной скорости, чтобы ее достичь требуется бесконечное количество энергии. Что осуществить невозможно. Скорость света является, предельной скоростью распространения материальных воздействий. Теория относительности Эйнштейна разрушила непрочные основы классических понятий пространства и времени. Она основывалась на двух постулатах.
Первый постулат – принцип относительности: все инерциальные системы отсчета эквивалентны друг другу в отношении постановки в них любых физических экспериментов.
Второй постулат – скорость света является постоянной во всех инерциальных системах отсчета и не зависит от движения источника и приемника, она одинакова во всех направлениях и равна 300 тыс. км/сек.
Движение любого объекта влияет на измеренную величину его длины. Неподвижному наблюдателю длина космического корабля показалась бы короче на величину, зависящую от скорости корабля.
В быстро движущемся космическом корабле время течет медленнее, чем в лаборатории неподвижного наблюдения. Эффект замедления времени касается буквально всего, включая процессы и даже биологические ритмы экипажа. Эффект замедления времени подтвержден многими экспериментами с космическими лучами.
Эйнштейн обнаружил еще одно следствие своей теории: масса тела зависит от скорости его движения чем ближе скорость тела к скорости света, тем больше становится его масса. При достижении телом скорости света, его масса возросла бы до бесконечности. Но достичь ее невозможно, так как требуется бесконечная энергия. В том же 1905 г. Эйнштейн установил связь между массой и энергией.
Масса тела есть мера содержащейся в нем энергии. В науке появилось знаменитое соотношение: Е=mc2, где Е–полная энергия тела; m–его масса покоя; с–скорость света;
Окружающий нас мир имеет три измерения. Но специальная теория относительности утверждает, что время нельзя рассматривать как нечто отдельное, неизменное. Немецкий математик Минковский высказал предположение, что три пространственные и одна временная размерность связаны между собой. Все события во Вселенной должны происходить в четырехмерном пространстве – времени. Эйнштейн быстро оценил преимущество такого описания для своей теории. Специальная теория относительности поистине произвела в революцию в нашем понимании пространства, времени, Вселенной. В отличие от пространства, в каждую точку которого можно снова и снова возвращаться – оно как бы обратимо, время – необратимо и одномерно. Оно течет из прошлого, через настоящее к будущему. Пространство – однородно и изотропно, а время однородно, эти свойства связаны с законами сохранения.
Заключение
Вклад, сделанный Ньютоном в развитие естествознания, заключался в том, что он дал математический метод обращения физических законов в количественно измеримые результаты, которые можно было подтвердить наблюдениями, и, наоборот, выводить физические законы на основе таких наблюдений. Как он сам писал в предисловии к "Началам", "... сочинение это нами предлагается как математические основания физики. Вся трудность физики... состоит в том, чтобы по явлениям движения распознать силы природы, а затем по этим силам объяснить остальные явления... Было бы желательно вывести из начал механики и остальные явления природы, рассуждая подобным же образом, ибо многое заставляет меня предполагать, что все эти явления обусловливаются некоторыми силами, с которыми частицы тел вследствие причин, пока неизвестных, или стремятся друг к другу и сцепляются в правильные фигуры, или же взаимно отталкиваются и удаляются друг от друга. Так как эти силы неизвестны, до сих пор попытки философов объяснить явления природы и оставались бесплодными. Я надеюсь, однако, что или этому способу рассуждения, или другому, более правильному, изложенные здесь основания доставят некоторое освещение".
Ньютоновский метод стал главным инструментом познания природы. Законы классической механики и методы математического анализа демонстрировали свою эффективность. Физический эксперимент, опираясь на измерительную технику, обеспечивал небывалую ранее точность. Физическое знание все в большей мере становилось основой промышленной технологии и техники, стимулировало развитие других естественных наук. В физике изолированные ранее свет, электричество, магнетизм и теплота оказались объединенными в электромагнитную теорию. И хотя природа тяготения оставалась не выясненной, его действия можно было рассчитать. Утвердилась концепция механистического детерминизма Лапласа, исходившая из возможности однозначно определить поведение системы в любой момент времени, если известные исходные условия. Структура механики как науки казалась прочной, надежной и почти полностью завершенной – т.е. не укладывающиеся в существующие классические каноны феномены, с которыми приходилось сталкиваться, казались вполне объяснимыми в будущем более изощренными умами с позиций классической механики. Складывалось впечатление, что знание физики близко к своему полному завершению – столь мощную силу демонстрировал фундамент классической физики.
С механической точки зрения можно говорить о покое, когда-то или иное тело не меняет своего пространственного положения, не перемещается относительно других тел. Лежащий камень, стоящая машина, сидящий человек покоятся, не меняют своего пространственного положения.
С количественной точки зрения покой имеет место тогда, когда вещи, объекты, в том числе живые организмы, не меняют существенно своих количественных характеристик - не увеличиваются и не уменьшаются в своих размерах. Например, достигнув определенного предела, прекращают рост растения, животные, человек.
С точки зрения качества покой - это пребывание вещи, объекта, организма, системы и т.д. в данном качественном состоянии, т.е. фиксируется момент качественной устойчивости. Это является непременным условием дифференциации материи, благодаря чему мы отличаем одни вещи от других. Возможность такого относительного покоя тел, возможность временного состояния равновесия является существенным условием дифференциации материи и тем самым существенным условием жизни.
Однако если движение абсолютно, ибо является способом существования материи, то покой не может быть абсолютным, а только относительным, ибо покой в одном отношении всегда связан с определенными изменениями в других отношениях. Покоящееся тело вместе с Землей вращается вокруг Солнца, вместе с Солнечной системой - вокруг центра (ядра) Галактики, которая также движется во Вселенной. Во взрослом организме уменьшается количество рождающихся и обновляющихся клеток, что ведет к его старению и, в конечном счете, к естественной смерти. В любом объекте происходят и незаметные качественные изменения.
Когда Н. Коперник доказал, что Земля не находится в центре Вселенной, а И. Кеплер раскрыл законы движения планет вокруг Солнца, затем Г. Галилей, а за ним и И. Ньютон показали, что земная и небесная механика выражают одни и те же законы движения материальных тел, были сделаны решительные шаги к познанию объективного единства мира. Данные спектрального анализа показали, что далекие космические тела, звезды, туманности состоят из тех же атомов химических элементов, что и все вещи на Земле. Трудами Ч.Р.Дарвина было доказано единство происхождения и развития живых организмов. Исследования М.Я. Шлейдена и Т. Шванна доказали единство клеточного строения всего живого. И. Сеченов и И.П. Павлов доказали материальную природу психики. Следовательно, естественные науки и философия дают новые и новые данные, подтверждающие идею о единстве мира. Материальный мир предстает как самоизменяющаяся, саморазвивающая целостность, а основными его свойствами являются: структурность, системность, взаимодействие, движение, самоорганизация, пространство, длительность, отражение.
Литература:
1. Гусейханов М. К. // Философские проблемы физики.Монография.-2010.
2. Омаров О. А., Гусейханов М. К. // История и методология физики.-М, Издательский дом «ЭКО», «Альтекс», 2005. - 244 с.
3. Некрасов А.И. Курс теоретической механики. т.1 Статика и кинематика 1956.
4.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.