
КРАЕВОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ
ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«АЛТАЙСКИЙ ТРАНСПОРТНЫЙ ТЕХНИКУМ»
ФОНД ОЦЕНОЧНЫХ СРЕДСТВ
по общеобразовательной дисциплине
«Математика» базовый уровень
с.Первомайское
2022
Составитель: Утева Л.П.
СОДЕРЖАНИЕ
1 Результаты обучения, регламентированные ФГОС СОО с учетом ФГОС СПО 3
2 Фонд оценочных средств для входного контроля 6
3 Фонд оценочных средств для текущего контроля 9
4 Фонд оценочных средств для рубежного контроля (по итогам 3.1 – 3.4) 31
5 Фонд оценочных средств для промежуточной аттестации 33
Предметные результаты на базовом уровне отражают:
ПРб 01. Владение методами доказательств, алгоритмами решения задач; умение формулировать определения, аксиомы и теоремы, применять их, проводить доказательные рассуждения в ходе решения задач;
ПРб 02. Умение оперировать понятиями: степень числа, логарифм числа; умение выполнять вычисление значений и преобразования выражений со степенями и логарифмами, преобразования дробно-рациональных выражений;
ПРб 03. Умение оперировать понятиями: рациональные, иррациональные, показательные, степенные, логарифмические, тригонометрические уравнения и неравенства, их системы;
ПРб 04. Умение оперировать понятиями: функция, непрерывная функция, производная, первообразная, определенный интеграл; умение находить производные элементарных функций, используя справочные материалы; исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций; строить графики многочленов с использованием аппарата математического анализа; применять производную при решении задач на движение; решать практико- ориентированные задачи на наибольшие и наименьшие значения, на нахождение пути, скорости и ускорения;
ПРб 05. Умение оперировать понятиями: рациональная функция, показательная функция, степенная функция, логарифмическая функция, тригонометрические функции, обратные функции; умение строить графики изученных функций, использовать графики при изучении процессов и зависимостей, при решении задач из других учебных предметов и задач из реальной жизни; выражать формулами зависимости между величинами;
ПРб 06. Умение решать текстовые задачи разных типов (в том числе на проценты, доли и части, на движение, работу, стоимость товаров и услуг, налоги, задачи из области управления личными и семейными финансами); составлять выражения, уравнения, неравенства и их системы по условию задачи, исследовать полученное решение и оценивать правдоподобность результатов;
ПРб 07. Умение оперировать понятиями: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах, дисперсия, стандартное отклонение числового набора; умение извлекать, интерпретировать информацию, представленную в таблицах, на диаграммах, графиках, отражающую свойства реальных процессов и явлений; представлять информацию с помощью таблиц и диаграмм; исследовать статистические данные, в том числе с применением графических методов и электронных средств;
ПРб 08. Умение оперировать понятиями: случайный опыт и случайное событие, вероятность случайного события; умение вычислять вероятность с использованием
графических методов; применять формулы сложения и умножения вероятностей, комбинаторные факты и формулы при решении задач; оценивать вероятности реальных событий; знакомство со случайными величинами; умение приводить примеры проявления закона больших чисел в природных и общественных явлениях;
ПРб 09. Умение оперировать понятиями: точка, прямая, плоскость, пространство, двугранный угол, скрещивающиеся прямые, параллельность и перпендикулярность прямых и плоскостей, угол между прямыми, угол между прямой и плоскостью, угол между плоскостями, расстояние от точки до плоскости, расстояние между прямыми, расстояние между плоскостями; умение использовать при решении задач изученные факты и теоремы планиметрии; умение оценивать размеры объектов окружающего мира;
ПРб 10. Умение оперировать понятиями: многогранник, сечение многогранника, куб, параллелепипед, призма, пирамида, фигура и поверхность вращения, цилиндр, конус, шар, сфера, сечения фигуры вращения, плоскость, касающаяся сферы, цилиндра, конуса, площадь поверхности пирамиды, призмы, конуса, цилиндра, площадь сферы, объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара; умение изображать многогранники и поверхности вращения, их сечения от руки, с помощью чертежных инструментов и электронных средств; умение распознавать симметрию в пространстве; умение распознавать правильные многогранники;
ПРб 11. Умение оперировать понятиями: движение в пространстве, подобные фигуры в пространстве; использовать отношение площадей поверхностей и объемов подобных фигур при решении задач;
ПРб 12. Умение вычислять геометрические величины (длина, угол, площадь, объем, площадь поверхности), используя изученные формулы и методы;
ПРб 13. Умение оперировать понятиями: прямоугольная система координат, координаты точки, вектор, координаты вектора, скалярное произведение, угол между векторами, сумма векторов, произведение вектора на число; находить с помощью изученных формул координаты середины отрезка, расстояние между двумя точками;
ПРб 14. Умение выбирать подходящий изученный метод для решения задачи, распознавать математические факты и математические модели в природных и общественных явлениях, в искусстве; умение приводить примеры математических открытий российской и мировой математической науки.
ОК 01 Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам
ОК 02 Использовать современные средства поиска, анализа и интерпретации информации, и информационные технологии для выполнения задач профессиональной деятельности
ОК 03 Планировать и реализовывать собственное профессиональное и личностное развитие, предпринимательскую деятельность в профессиональной сфере, использовать знания по финансовой грамотности в различных жизненных ситуациях
ОК 04 Эффективно взаимодействовать и работать в коллективе и команде ОК 05 Осуществлять устную и письменную коммуникацию на государственном языке Российской Федерации с учетом особенностей социального и культурного контекста
ОК 06 Проявлять гражданско-патриотическую позицию, демонстрировать осознанное поведение на основе традиционных общечеловеческих ценностей, в том числе с учетом гармонизации межнациональных и межрелигиозных отношений, применять стандарты антикоррупционного поведения
ОК 07 Содействовать сохранению окружающей среды, ресурсосбережению, применять знания об изменении климата, принципы бережливого производства, эффективно действовать в чрезвычайных ситуациях
Профессиональные компетенции по профессии 35.01.19 Эксплуатация и ремонт и ремонт сельскохозяйственных машин
ПК 1.1- ПК 1.10.
Входной контроль состоит из заданий, частично взятых из открытого банка ОГЭ и ВПР по математике. На выполнение заданий входного контроля дается 1 академический час (45 минут). Входной контроль состоит их 2-х частей: обязательной и дополнительной. Обязательная часть содержит задания минимального обязательного уровня,
дополнительная часть – более сложные задания.
При выполнении заданий требуется представить ход решения и указать полученный ответ. Правильно выполненное задание из обязательной части оценивается в один балл; правильное выполнение заданий дополнительной части оценивается 2 баллами или 0-1 баллами за частичное решение.
Баллы, полученные за все выполненные задания, суммируются.
|
Отметка |
Число баллов, необходимое для получения отметки |
|
«3» (удов.) |
7-9 |
|
«4» (хорошо) |
10-12 |
|
«5» (отлично) |
13-15 |
Образовательные результаты, подлежащие проверке (элементы):
ПРб 1, ПРб 5, ПРб 6, ПРб 9, ПРб 12,ПРб 14.
ОК 01, ОК 02, ОК 04, ОК 05, ОК 06.
ПК 1.1- ПК 1.10
Задания входного контроля Обязательная часть:
1. 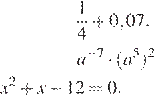 (1
балл) Найдите значение выражения
(1
балл) Найдите значение выражения
2. (1 балл) Найдите значение выражения при a = 5.
3. (1 балл) Решите уравнение
4. (1 балл) На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
5. (1 балл) Установите соответствие между графиками функций и формулами, которые их задают.
А) Б) В)
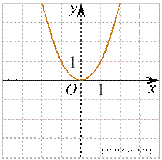
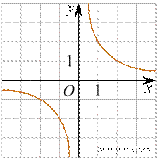
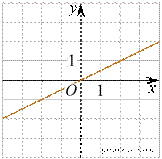
![]() 1)
1)
2)
3)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.

На каком рисунке изображено множество еѐ решений?
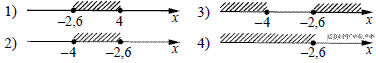
1) 1
2) 2
3) 3
4) 4
8.(1 балл) В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ВАС. Ответ дайте в градусах. 9(1 балл). Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. 2) Треугольник со сторонами 1, 2, 4 существует.
3) В любом параллелограмме есть два равных угла.
Дополнительная часть
При выполнении заданий 10-12 запишите ход, обоснование решения и полученный ответ.
10.(2 балла) Решите уравнение ![]()
11.(2 балла) В прямоугольном треугольнике ABC с прямым углом C известны катеты: AC = 6 , BC = 8 . Найдите медиану CK этого треугольника.
12.(2 балла) Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Ответ |
Б |
Б |
В |
А |
2,7 |
2 |
9 |
816 |
8 |
Текущий контроль проводятся во время аудиторных занятий по математике в соответствии с учебным планом и рабочей программы ОД «Математика» по всем разделам программы. Текущий контроль состоит из двух частей: теоретической и практической. При этом обучающиеся получают две отметки.
Теоретическая часть проходит в форме устных ответов: обучающиеся вытягивают пять карточек с вопросами, дают полный ответ (со списком вопросов обучающиеся знакомятся в начале изучения раздела).
Шкала перевода баллов в отметки по пятибалльной системе
|
Отметка |
Количество верных ответов на теоретические вопросы |
|
«3» (удов.) |
3 |
|
«4» (хорошо) |
4 |
|
«5» (отлично) |
5 |
Задания практической части (контрольные работы) частично взяты из открытого банка ЕГЭ и ВПР по математике.
На выполнение контрольной работы по математике дается 1 академический час (45 минут).
Контрольная работа состоит их 2-х частей. В первой части предлагается выполнить 4 задания - выбрать правильный ответ из четырех предложенных. Во второй части предлагается выполнить 6 заданий - оформить ход решения и записать полученный ответ.
За правильное выполнение любого задания первой части обучающийся получает один балла. Правильное выполнение заданий второй части оценивается 2 баллами или 1 баллом за частичное решение.
Баллы, полученные за все выполненные задания, суммируются.
Шкала перевода баллов в отметки по пятибалльной системе
|
Отметка |
Число баллов, необходимое для получения отметки |
|
«3» (удов.) |
8-10 |
|
«4» (хорошо) |
11-13 |
|
«5» (отлично) |
14-16 |
3.1 Прямые и плоскости в пространстве
Образовательные результаты, подлежащие проверке (элементы):
ПРб 1, ПРб 9,ПРб 11, ПРб 12, ПРб 14.
ОК 01, ОК 02, ОК 03, ОК 05,
ПК 1.1- ПК 1.10
Теоретические вопросы:
1. Сформулируйте теорему Пифагора.
2. Перечислите основные фигуры в пространстве.
3. Перечислите способы задания плоскости.
4. Продолжите теорему: «Если одна из двух параллельных прямых перпендикулярна плоскости, то…».
5. Продолжите теорему: «Если две параллельные плоскости пересекаются третьей, то…».
6. Сформулируйте определение двуграного угла.
7. Сформулируйте определение трехграного угла.
8. Раскройте понятие «угол между прямыми».
9. Перечислите взаимное расположение двух прямых в пространстве 10. Какие прямые называются параллельными в пространстве?
11. Какие прямые называются скрещивающимися в пространстве?
12. Какие прямые называются перпендикулярными в пространстве?
13. Перечислите взаимное расположение прямой и плоскости в пространстве.
14. Раскройте понятие «угол между прямой и плоскостью».
15. Раскройте понятие «параллельность прямой и плоскости».
16. Раскройте понятие «перпендикулярность прямой и плоскости».
17. Перечислите взаимное расположение двух плоскостей в пространстве.
18. Раскройте понятие «угол между плоскостями».
19. Раскройте понятие «параллельность плоскостей».
20. Раскройте понятие «перпендикулярность плоскостей».
21. Как найти расстояние от точки до прямой?
22. Как найти расстояние между прямыми?
23. Как найти расстояние между плоскостями?
24. Продолжите определение: «Перпендикуляр – это…».
25. Продолжите определение: «Наклонная – это…».
26. Продолжите определение: «Проекция наклонной – это…».
27. Перечислите свойства параллельного проектирования.
28. Приведите примеры симметрий на плоскости в природе, искусстве, архитектуре, в вашей профессии.
29. Приведите примеры симметрий в пространстве в природе, искусстве, архитектуре
30. Встречается ли где-нибудь в вашей профессии угол между прямой и плоскостью?
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
1. (1 балл) Расшифруйте краткую запись: a∈ 𝛽.
А) точка a принадлежит плоскости 𝛽; Б) точка a принадлежит прямой 𝛽; В) прямая a принадлежит плоскости 𝛽; Г) прямая a пересекает плоскость 𝛽.
2. (1 балл) Прямые АВ и СД скрещиваются. Какое расположение имеют прямые АС и ВД? А) параллельные; Б) перпендикулярные; В) скрещиваются; Г) пересекаются.
3. (1 балл) Плоскости 𝛼 и 𝛽 имеют 1 общую точку. Каково их взаимное расположение?
А) параллельны; Б) пересекаются по прямой; В) совпадают; Г) скрещиваются.
4. (1 балл) Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она…
А) перпендикулярна и самой наклонной; Б) параллельна и самой наклонной; В) скрещивается с
наклонной; Г) перпендикулярна основанию наклонной.
При выполнении заданий 5-8 запишите ход решения и полученный ответ.
5. (2 балла) Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1 и М1. Найдите длину отрезка ММ1, если отрезок АВ не пересекает плоскость и АА1=6,8см, ВВ1=7,4см.
6. (2 балла) Прямые АС, АВ и АД попарно перпендикулярны. Найдите отрезок СД, если АВ=5 см, ВС=13 см, АД=9 см.
7. (2 балла) Из точки к плоскости проведены две наклонные. Найдите длины общего перпендикуляра, если проекции наклонных относятся как 2:3 и длины наклонных равны 23 см и 33 см.
8. (2 балла) Начертить куб АВСДА1В1С1Д1. Построить точку К∈АВ, точку М∈ДД1С, отрезок РЕ∈А1В1С1.
1. (3
балла)  Проверку глубины вспашки наиболее быстро и
надежно производить с помощью бороздомера, который состоит из двух линеек
одинаковой длины: неподвижной l, оканчивающейся угольником, и подвижной m. Для
замера глубины пахоты бороздомер устанавливают вертикально угольником на
непаханую землю, а подвижную линейку опускают на расчищенное дно борозды.
Верхний конец подвижной линейки показывает глубину борозды по шкале, нанесенной
от верхнего конца неподвижной линейки. Докажите, что длина отрезка АВ
неподвижной линейки бороздомера равна глубине борозды.
Проверку глубины вспашки наиболее быстро и
надежно производить с помощью бороздомера, который состоит из двух линеек
одинаковой длины: неподвижной l, оканчивающейся угольником, и подвижной m. Для
замера глубины пахоты бороздомер устанавливают вертикально угольником на
непаханую землю, а подвижную линейку опускают на расчищенное дно борозды.
Верхний конец подвижной линейки показывает глубину борозды по шкале, нанесенной
от верхнего конца неподвижной линейки. Докажите, что длина отрезка АВ
неподвижной линейки бороздомера равна глубине борозды.
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Ответ |
В |
В |
Б |
А |
7,1 |
15 |
9 |
- |
- |
Образовательные результаты, подлежащие проверке (элементы):
ПРб 1, ПРб 9, ПРб 11, ПРб 12, ПРб 13. ОК 01, ОК 02, ОК 03, ОК 05.
ПК 1.1- ПК 1.10
Теоретические вопросы:
1. Из чего состоит прямоугольная система координат в пространстве?
2. Если точка лежит в плоскости ху, какая координата у нее нулевая?
3. Приведите пример координат точки А, которая лежит на оси z.
4. Раскройте понятие «вектор».
5. Как найти координаты вектора?
6. Перечислите и раскройте правила сложения векторов.
7. Какие векторы называются коллинеарными?
8. Какие векторы называются перпендикулярными?
9. Чему равно скалярное произведение векторов?
10. Чему равен угол между векторами?
Контрольная работа
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
1. (1 балл) Даны точки А(1;0;5), В(-2;0;4), С(0;-1;0), Д(0;0Ф;2). Какие из них лежат на координатной прямой Оу?
А) А; Б) В; В) С; Г) Д.
2. (1 балл) Какие из векторов а(1;0;-1), с(1/3;2/3;-2/3), в(1;1;1), р(0;0;-2) являются единичными? А) а; Б) с; В) в; Г) р.
3. (1 балл) Какие из векторов а(1;2;-3), с(3;6;-6), в(2;4;-6) коллинеарные?
?А) а, в; Б) с, в; В) а, с; Г) коллинеарных векторов нет.
4. (1 балл) Даны точки А(2,0,5), В(2,4,-2) С(-2,6,3). Серединой какого отрезка является точка М(0,3,4)?
А) АВ; Б) ВС; В) АС; Г) СВ.
При выполнении заданий 5-8 запишите ход решения и полученный ответ.
5. (2 балла) Даны векторы а(-6,0,8) , в(-3;2;-6). Найдите скалярное произведение векторов.
![]()
6. (2 балла) При каких значениях п векторы а (4;п;2), в (1;2;п) перпендикулярны?)
7. (2 балла) Даны векторы а(-6;0;8), в(-3;2;-6). Найдите косинус угла между векторами.
8. (2 балла) Докажите, что четырѐхугольник АВСД является ромбом, если: А(6;7;8), В(8;2;6), С(4;3;2), Д(2;8;4).
При выполнении задания 9 запишите ход, обоснование решения и полученный ответ.
9. (3 балла) Участок представлен на координатной плоскости. Найдите площадь участка (четырехугольника), вершины которого имеют координаты (8;0), (10;8), (2;10), (0;2).

Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Ответ |
В |
В |
А |
В |
-30 |
-1 |
-3/7 |
- |
68 |
3.3 Основы тригонометрии. Тригонометрические функции
Образовательные результаты, подлежащие проверке (элементы):
ПРб 1, ПРб 3, ПРб 5, ПРб 14. ОК 01, ОК 02, ОК 03, ОК 05.
Теоретические вопросы:
1. Чему равен угол в один радиан?
2. В каких четвертях тригонометрического круга функция у=sinх принимает положительные значения?
3. В каких четвертях тригонометрического круга функция у= cosx принимает отрицательные значения?
4. Продолжите определение: «Синус острого угла – это…».
5. Продолжите определение: «Косинус острого угла – это…».
6. Продолжите определение: «Тангенс острого угла – это…».
7. Сформулируйте основное тригонометрическое тождество.
8. Чему равно произведение tgx*ctgx?
9. Чему равен sin(2x)? Сформулируйте правило вычисления.
10. Чему равен cos(2x)? Сформулируйте правило вычисления.
11. Перечислите тригонометрические функции, укажите их периоды.
12. Чему равен период функции y=cos(4x)?
13. ему равен период функции y=cos(x/4)?
14. Определите область значения функции y=3cos(5x)?
15. Перечислите способы решения тригонометрических уравнений.
16. Раскройте алгоритм решения однородных тригонометрических уравнений первого порядка.
17. Раскройте алгоритм решения однородных тригонометрических уравнений второго порядка.
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
|
|
|
|
3.4 Производная функции, ее применение
Образовательные результаты, подлежащие проверке (элементы):
ПРб 1, ПРб 4, ПРб 6, ПРб 14. ОК 01, ОК 02, ОК 03, ОК 05.
ПК 1.1- ПК 1.10
Теоретические вопросы:
1. Продолжите определение: «Последовательность – это…».
2. Приведите пример арифметической прогрессии.
3. Приведите пример геометрической прогрессии.
4. Приведите пример бесконечно убывающей геометрической прогрессии.
5. Продолжите определение: «Производная – это…».
6. Раскройте геометрический смысл производной.
7. Продолжите определение: «Касательная – это…».
8. Раскройте физический смысл производной.
9. Перечислите правила вычисления производных.
10. Чему равна производная степенной функции?
11. Чему равна производная произведения?
12. Чему равна производная частного?
13. Чему равна производная сложной функции?
14. Сформулируйте признак возрастания функции.
15. Сформулируйте признак убывания функции.
16. Сформулируйте признак точки максимума функции.
17. Сформулируйте признак точки минимума функции.
18. Составьте алгоритм решения задач на нахождения наибольшего и наименьшего значения функции на отрезке?
19. Составьте алгоритм исследования и построения графика функции с помощью производной.
20. Как найти вертикальную асимптоту графика функции?

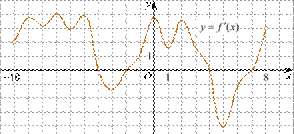
А) 5; Б) 4; В) 2; Г) 3.
При выполнении заданий 5-8 запишите ход решения и полученный ответ.
5.(2 балла) Материальная точка движется прямолинейно по закону
![]() (где
x — расстояние от точки отсчета в метрах, t — время в
(где
x — расстояние от точки отсчета в метрах, t — время в
секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени
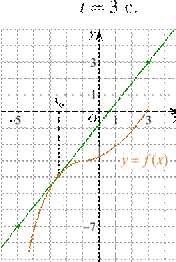 6.(2 балла) На
рисунке изображѐн график функции y = f(x)
и касательная к нему в точке с абсциссой x0. Найдите значение
производной функции f(x) в точке x0.
6.(2 балла) На
рисунке изображѐн график функции y = f(x)
и касательная к нему в точке с абсциссой x0. Найдите значение
производной функции f(x) в точке x0.
7.(2 балла) Решите
неравенство: (![]() х−2)(х+3) > 0
х−2)(х+3) > 0
(х−8)
8.(2 балла) Исследовать функцию f(х)=х3 – 3х и построить еѐ график.
При выполнении задания 9 запишите ход, обоснование решения и полученный ответ. 9.(3 балла) Требуется изготовить поддон для слива отработанного ГСМ - открытую сверху коробку, вырезая по углам равные квадратики. Прямоугольный лист жести имеет длину 64 см и ширину 40 см. Каковы должны быть стороны вырезаемых квадратиков,
чтобы вместимость поддона была максимальной.
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Ответ |
В |
Б |
А |
В |
8 |
1,25 |
(-3; 2), (8; +∞) |
- |
8 |
Образовательные результаты, подлежащие проверке (элементы): ПРб 1, ПРб 6, ПРб 9, ПРб 10, ПРб 11, ПРб 12, ПРб 14.
ОК 01, ОК 02, ОК 03, ОК 04, ОК 05, ОК 06, ОК 07.
ПК 1.1- ПК 1.10
Теоретические вопросы:
1. Продолжите определение: «Многогранник – это…».
2. Продолжите определение: «Призма – это…».
3. Продолжите определение: «Прямоугольный параллелепипед – это…».
4. Продолжите определение: «Куб – это…».
5. Продолжите определение: «Пирамида – это…».
6. Сформулируйте свойство о противолежащих гранях параллелепипеда.
7. Сформулируйте свойство о диагоналях параллелепипеда.
8. Сформулируйте свойство о диагонали и линейных размерах прямоугольного параллелепипеда.
9. Какая призма называется прямой?
10. Какая призма называется правильной?
11. Раскройте понятие «правильная пирамида».
12. Что такое апофема правильной пирамиды?
13. В чем отличие полной поверхности призмы от полной поверхности пирамиды?
14. Сформулируйте теорему о вычислении боковой поверхности прямой призмы.
15. Сформулируйте теорему о вычислении боковой поверхности правильной пирамиды.
16. Назовите предметы из вашей профессиональной деятельности, которые имеют формы многогранников.
17. Какие многогранники называются правильными? Перечислите правильные многогранники.
18. Продолжите определение: «Цилиндр – это…».
19. Продолжите определение: «Конус – это…».
20. Продолжите определение: «Усеченный конус – это…».
21. Продолжите определение: «Шар – это…».
22. Что является высотой усеченного конуса?
23. Что является осевым сечением цилиндра, конуса, усеченного конуса, шара?
24. Перечислите единицы измерения площади, объема. 25. Чему равно отношение площадей поверхностей подобных фигур в пространстве?
26. Чему равно отношение объемов подобных фигур в пространстве?
27. Назовите предметы из вашей профессиональной деятельности, которыеимеют формы тел вращения.
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
1. (1 балл) В каких единицах измеряется площадь поверхности многогранника?
А) в градусах; Б) в метрах; В) в квадратных метрах; Г) в двугранных градусах.
2. (1 балл) Площадь боковой поверхности призмы вычисляется по формуле А) S = Sбок + 2 SОСН.; Б) Sбок =Росн*H; В) S = Рбок + S S ОСН; Г) Sбок =2Росн*H.
3. (1 балл) Что является осевым сечением усеченного конуса?
А) равнобедренный треугольник; Б) равнобедренная трапеция; В) прямоугольник; Г) прямоугольная трапеция.
4. (1 балл) Какая фигура получается при вращении прямоугольного треугольника вокруг одного из своих катетов?
А) конус; Б) усеченный конус; В) пирамида; Г) усеченная пирамида.
При выполнении заданий 5-8 запишите ход решения и полученный ответ.
5. (2 балла) Ребро основания правильной треугольной пирамиды 3 м, апофема 6м. Найдите площадь боковой поверхности пирамиды.
6. (2 балла) Диагональ
куба равна ![]() Найдите его объем. 7. (2
балла) Прямоугольник со сторонами 8см и 3см вращается вокруг большей стороны.
Найдите его объем. 7. (2
балла) Прямоугольник со сторонами 8см и 3см вращается вокруг большей стороны.
Найдите объем, площади боковой и полной поверхностей полученного тела.
8. (2 балла) Вычислить площадь поверхности подшипника, радиуса 0,5 м. В ответ запишите число, деленное на
При выполнении задания 9 запишите ход, обоснование решения и полученный ответ.
9 (2 балла) Кузов тракторного прицепа имеет вид усеченной пирамиды размерами: вверху 3,5 м х 2,6 м, понизу 2,9 м х 1,1 м. Найдите вместимость, если высота прицепа 1,2 м. Предполагаемые модели клумб:
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Ответ |
В |
Б |
Б |
А |
27 |
2744 |
72 π; 48 π; 64 π |
1 |
7 м3
|
Образовательные результаты, подлежащие проверке (элементы):
ПРб 1, ПРб 4,ПРб 6, ПРб 14.
ОК 01, ОК 02, ОК 03, ОК 05.
ПК 1.1- ПК 1.10 .
Теоретические вопросы:
1. Продолжите определение: «Функция F(x) называется …».
2. Раскройте геометрический смысл определенного интеграла.
3. Продолжите определение: «Криволинейная трапеция – это…».
4. Сформулируйте формулу Ньютона-Лейбница.
5. В чем заключается общий вид всех первообразных?
6. Перечислите правила вычисления интегралов.
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
1. (1 балл) Для какой из функций функция F(х)=х3-3х2+1 является первообразной? А) f(х)=3(х2-2); Б) f(х)=3х(х2-2); В) f(х)=3х2-6х+1; Г) f(х)=3х2-6х.
2. (1 балл) Дана функция f(х)= 3х2+1. Чему равна F(1)
1
А) 2; Б) 4; В) 6; Г) 1
3
3. (1 балл) Общий вид всех первоообразных для f(х)=sinx?
А) F(х)=cosx+C; Б) F(х)=-cosx+C; В) F(х)=tgx+C; Г) F(х)=-tgx+C.
2
4. (1 балл) Вычислите определенный интеграл ∫1 𝑥𝑑𝑥. А) -1; Б) 1; В) -1,5; Г) 1,5.
При выполнении заданий 5-8 запишите ход решения и полученный ответ.
5. (2 балла) Является ли F(х)=х3-3х+1 первообразной для функции f(х)=3(х2-1)?
6. (2 балла) Задайте первообразную F(х) для функции f(х)=3х2-2х, если известны координаты точки М (1, 4) графика F(х).
7. (2 балла) На рисунке изображен график функции y=f(x), определѐнной на интервале (−3; 11). Найдите наименьшее значение функции f(x)на отрезке [2; 9,5].
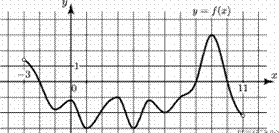
8. (2 балла) На рисунке изображен график некоторой функции y=f(x). Пользуясь рисунком,
5
![]() вычислите
определенный интеграл∫ 𝑓(𝑥)𝑑𝑥. 1
вычислите
определенный интеграл∫ 𝑓(𝑥)𝑑𝑥. 1

При выполнении задания 9 запишите ход, обоснование решения и полученный ответ.
9. (3 балла) Вычислить площадь поля, периметр которой ограничивают линии у=0, y=х, y=-2х+6. Решить двумя способами. Сделать чертеж. Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Ответ |
Г |
А |
Б |
Г |
да |
х -х2+4 3 |
-3 |
12 |
3 |
Образовательные результаты, подлежащие проверке (элементы):
ПРб 1, ПРб 2, ПРб 3, ПРб 5, ПРб 6, ПРб 14. ОК 01, ОК 02, ОК 03, ОК 04, ОК 05, ОК 06.
Теоретические вопросы:
1. Сформулируйте определение степенной функции.
2. Перечислите свойства степенной функции с целым показателем.
3. Перечислите свойства степени с действительным показателем. Приведите примеры.
4. Перечислите свойства корня натуральной степени. Приведите примеры
5. На что необходимо обратить внимание при решении иррационального уравнения четной степени?
6. Чему равен корень четной степени из отрицательного числа? Приведите пример.
7. Чему равен корень нечетной степени из отрицательного числа? Приведите пример.
8. На что стоит обратить внимание при решении иррациональных, дробно- рациональных уравнений и неравенств?
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.ножая числа с одинаковым основанием, их степени…?

Дополнительная часть При выполнении задания 9 запишите ход, обоснование решения и полученный ответ.
![]()
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Ответ |
Б |
Г |
В |
В |
49 |
2 |
0,18 |
-36 |
(1; 1) |
Образовательные результаты, подлежащие проверке (элементы):
ПРб 1, ПРб 2,ПРб 3, ПРб 4, ПРб 5, ПРб 6, ПРб 14. ОК 1, ОК 2, ОК 3, ОК 5.
Теоретические вопросы:
1. Сформулируйте определение показательной функции.
2. Перечислите свойства показательной функции.
3. Перечислите способы решения показательных уравнений.
4. Сформулируйте правило решения простейших показательных неравенств.
5. В чем заключается графический способ решения уравнений.
6. Приведите пример функциональной зависимости показательной функции из реальной жизни.
Контрольная работа
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
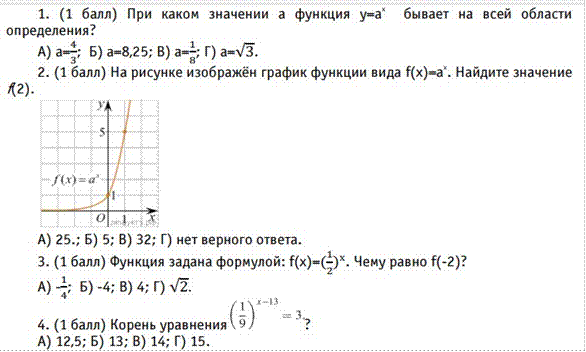
При выполнении заданий 5-8 запишите ход решения и полученный ответ.
![]()

Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Ответ |
В |
А |
В |
А |
1 |
2 |
-4 |
21 |
(2; 4) |
Образовательные результаты, подлежащие проверке (элементы):
ПРб 1, ПРб 2, ПРб 3, ПРб 4, ПРб 5, ПРб 6, ПРб 14. ОК 1, ОК 2, ОК 3, ОК 5.
Теоретические вопросы:
1. Сформулируйте определение логарифмической функции.
2. Перечислите свойства логарифмической функции.
3. Продолжите определение: «Логарифм – это…».
4. Чему равен логарифм произведения?
5. Чему равен логарифм частного?
6. Приведите примеры логарифмической спирали в природе и в окружающем мире.
7. На что стоит обратить внимание при решении логарифмических и уравнений и неравенств?
8. Перечислите способы решения логарифмических уравнений.
9. Сформулируйте правило решения простейших логарифмических неравенств.
10. В чем заключается графический способ решения уравнений.
11. Приведите пример функциональной зависимости логарифмической функции из реальной жизни.
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.


Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Ответ |
А |
Г |
А |
Б |
5 |
3 |
-6 |
34 |
(0; 3) |
3.10 Элементы комбинаторики, статистики и теории вероятностей
Образовательные результаты, подлежащие проверке (элементы):
ПРб 7, ПРб 8, ПРб 14.
ОК 1, ОК 2, ОК 3, ОК 5.
ПК 1.1- ПК 1.10
Теоретические вопросы:
1. Продолжите определение: «Случайное событие – это…». Приведите пример.
2. Приведите пример достоверного события.
3. Приведите пример невозможного события.
4. Продолжите определение: «Вероятность случайного события – это…».
5. Сформулируйте правило нахождения сложения вероятностей.
6. Сформулируйте правило умножения вероятностей.
7. Как найти среднее арифметическое числового ряда?
8. Как найти медиану числового ряда?
9. Как вычисляется размах числового ряда?
10. Для чего нужны диаграммы, графики? Перечислите виды диаграмм.
11. Приведите примеры проявления закона больших чисел в природных явлениях.
12. Приведите примеры проявления закона больших чисел в общественных явлениях.
13. Что изучает статистика?
14. Продолжите определение: «Сочетание – это…».
15. Продолжите определение: «Размещение – это…».
16. Продолжите определение: «Перестановки – это…».
Обязательная часть При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
При решении заданий 1-4 запишите правильный ответ из четырех предложенных
1. (1 балл) Каких событий не бывает в теории вероятностей? А) случайные; Б) неслучайные; В) достоверные; Г) невозможные.
2. (1 балл) Событие, которое при выполнении определенной совокупности условий, обязательно произойдет - это:
А) случайное; Б) неслучайное; В) достоверное; Г) невозможное.
3. (1 балл) Вероятность случайного события есть неотрицательное число, заключенное между числами:
А) 0 и 1; Б) 0 и 100; В) -1 и 1; Г) -100 и 100.
4. (1 балл) Группировка – это…
А) упорядочение единиц совокупности по признаку; Б) разбиение единиц совокупности на группы по признаку; В) обобщение единичных фактов; Г) обобщение единичных признаков.
5. (2 балла) В офисе дилерского центра «John Deere» находятся 8 посетителей мужского пола и 2 женского. Определить вероятность того, что первым к консультанту обратится женщина. 6. (2 балла) На конференцию приехали 2 студента из с.Первомайское, 3 из Павловска и 7 из Барнаула. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьѐвкой. Найдите вероятность того, что пятым окажется доклад студента из Барнаула.
7. (2 балла) Миша, Тимур, Денис, Костя и Антон пришли на демонстрационный экзамен.
Эксперт начал жеребьевку. Найдите вероятность того, что первым в жеребьевке не будет Антон. 8. (2 балла) В среднем из 2000 топливных насосов,поступивших в продажу,6 подтекают.
порядке. Какова вероятность того, что один случайно выбранный для контроля насос не подтекает?
9. (2 балла) Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169. Найдите моду ряда и среднее арифметическое ряда.
10. (2 балла) При анализе ценовых предпочтений клиентов на приобретение запчастей получены данные, представленные в таблице: доля клиентов, приобретающих запчасти одинакового назначения, но различной цены. Найти моду случайной величины. Х – цены продаваемых услуг.
|
xi |
3500 |
4500 |
5500 |
6500 |
7500 |
8500 |
|
pi |
1/20 |
3/20 |
3/20 |
8/20 |
4/20 |
1/20 |
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Ответ |
Б |
В |
А |
А |
0,2 |
0,25 |
0,8 |
0,997 |
172; 172,75 |
6500 |
3.11 Уравнения и неравенства
Образовательные результаты, подлежащие проверке (элементы):
ПРб 2, ПРб 3, ПРб 14.
ОК 1, ОК 2, ОК 3, ОК 5.
Теоретические вопросы:
1. Что называется уравнением?
2. Что значит решить уравнение?
3. Что такое корень уравнения?
4. Что называется неравенством?
5. Что значит решить неравенство?
6. В чем заключается «метод интервалов»?
7. Что называется решение системы уравнений?
8. Что значит решить систему уравнений?
9. При решении каких уравнений и неравенств, следует обратить внимание на область допустимых значений?
10. Перечислите способы решения уравнений.
11. Перечислите способы решения систем уравнений.
При решении заданий 1-4 запишите правильный ответ из четырех предложенных:
1. (1 балл) Какое из чисел является корнем уравнения log2(х+1)=1 А) –1; Б) 2; В) 1; Г)
0.
2. (1 балл) Какие из уравнений имеют более одного корня?
А) х -6х+5=0; Б) 3 =9; В) (х-4)(х+3)(х-8)=0; Г) 2х-7=0.
3. (1
балл) Определите вид уравнения ![]()
А) линейное; Б) квадратное; В) иррациональное; Г) рациональное.
4. (1 балл) Определите наименьшее целое решение неравенства 5х+2<1?
А) -3; Б) 0; В) 3; Г) -4.
При выполнении заданий 5-8 запишите ход решения и полученный ответ.
5. (2 балла) Найдите корень уравнения │х-3│=2
6. 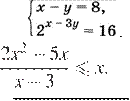 (2
балла) Решите систему уравнений
(2
балла) Решите систему уравнений
7. (2 балла) Решите неравенство
8. (2 балла) Решите уравнение (2х − 3)√3х2 − 5х − 2=0
При выполнении задания 9 запишите ход, обоснование решения и полученный ответ.
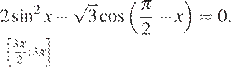 9. (3 балла) Решите уравнение
. Укажите корни этого уравнения, принадлежащие отрезку
9. (3 балла) Решите уравнение
. Укажите корни этого уравнения, принадлежащие отрезку
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Ответ |
В |
А, В |
В |
А |
1; 5 |
(10; 2) |
|
-1; 6 |
|
Образовательные результаты, подлежащие проверке (элементы):
ПРб 1, ПРб 3, ПРб 4, ПРб 5, ПРб 6, ПРб 9, ПРб 11, ПРб 12, ПРб 14. ОК 01, ОК 02, ОК 03 ОК 05.
ПК 1.1- ПК 1.10
При решении заданий 1-4 запишите правильный ответ из четырех предложенных.
1. (1 балл) Даны точки А(2,0,5), В(-2,6,3). Какие координаты имеет середина отрезка АВ
– точка М?
А) М(0; 3; 4); Б) М(2; 3; 4); В) М(0;- 3;4); Г) М(0;3;- 4).
2. (1 балл) Прямые АВ и СД параллельные. Какое расположение имеют прямые АС и ВД? А) параллельные; Б) перпендикулярные; В) скрещиваются; Г) пересекаются.
![]()
3. (1 балл) Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.
А) -3; Б) 0; В) -2; Г) -1.
4. (1 балл) На рисунке изображен график производной функции y=f(x). При каком значении x функция принимает свое наибольшее значение на отрезке [-4; -2] ?
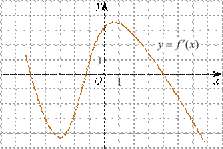
А) 0,5; Б) -4; В) -5; Г) 1.
При выполнении заданий 5-8 запишите ход решения и полученный ответ.
5. (2 балла) Верхние концы двух вертикально стоящих столбов, удалѐнных на расстояние 4 м, соединены перекладиной. Высота одного столба 10 м, а другого 7 м. Найдите длину перекладины.
6. (2 балла) Даны четыре точки: А(0;1;1), В(1;-1;3), С(3;1;0) Д(3;2;2) Докажите, что отрезки АВ и СД перпендикулярны.
7.
![]() (2 балла) Двигаясь со
скоростью
(2 балла) Двигаясь со
скоростью ![]() м/с, трактор тащит сани с силой F=40 кН,
направленной под острым углом к горизонту. Мощность, развиваемая
трактором, вычисляется по формуле Найдите, при
каком угле (в градусах) эта мощность будет равна 60 кВт.
м/с, трактор тащит сани с силой F=40 кН,
направленной под острым углом к горизонту. Мощность, развиваемая
трактором, вычисляется по формуле Найдите, при
каком угле (в градусах) эта мощность будет равна 60 кВт.
8. (2 балла) Материальная точка движется прямолинейно по закону x(t)=t2-13t+23 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
При выполнении задания 9 запишите ход, обоснование решения и полученный ответ. 9. (2 балла) Каким должно быть отношение диаметра основания к высоте закрытой цилиндрической цистерны, чтобы при заданном объеме на изготовление цистерны шло как можно меньше материала
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Ответ |
А |
Г |
Г |
Б |
5 |
- |
60 |
8 |
1 |
На выполнение письменной экзаменационной работы по математике дается 4 астрономических часа (240 минут). Экзаменационная работа состоит их 2-х частей: обязательной и дополнительной.
Обязательная часть содержит задания минимального обязательного уровня, дополнительная часть – более сложные задания.
При выполнении заданий обязательной части требуется представить ход решения и указать полученный ответ. За правильное выполнение любого задания из обязательной части обучающийся получаете один балл. При выполнении задания из дополнительной части необходимо подробно описать ход решения и дать ответ. Правильное выполнение заданий дополнительной части оценивается 3 баллами или 1- 2 баллами за частичное решение. Баллы, полученные за все выполненные задания, суммируются.
Шкала перевода баллов в отметки по пятибалльной системе
|
Отметка |
Число баллов, необходимое для получения отметки |
|
«3» (удов.) |
6-9 |
|
«4» (хорошо) |
10-14 (не менее одного задания из дополнительной части) |
|
«5» (отлично) |
более 14 (не менее двух заданий из дополнительной части) |
Образовательные результаты, подлежащие проверке (элементы):
ПРб 1, ПРб 2, ПРб 3, ПРб 4, ПРб 5, ПРб 6, ПРб 7,ПРб 8, ПРб 9,ПРб 10, ПРб 11, ПРб 12, ПРб 13, ПРб 14.
ОК 01, ОК 02, ОК 03, ОК 05. ПК 1.1- ПК 1.10 Экзаменационные задания по математике
При выполнении заданий 1-12 запишите ход решения и полученный ответ.
 1. (1
балл) Вычислите: 2sin(π/6)+2cos(π/3) 2. (1
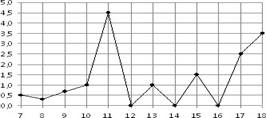
балл) На рисунке жирными точками показано суточное количество осадков,
выпадавших в Элисте с 7 по 18 декабря 2001 года. По горизонтали указываются числа
месяца, по вертикали — количество осадков, выпавших в
соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке
соединены линией. Определите по рисунку, сколько дней выпадало более 2
миллиметров осадков?
1. (1
балл) Вычислите: 2sin(π/6)+2cos(π/3) 2. (1
балл) На рисунке жирными точками показано суточное количество осадков,
выпадавших в Элисте с 7 по 18 декабря 2001 года. По горизонтали указываются числа
месяца, по вертикали — количество осадков, выпавших в
соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке
соединены линией. Определите по рисунку, сколько дней выпадало более 2
миллиметров осадков?
3. (1 балл)Аккумулятор для трактора МТЗ стоил 16000 рублей. Через некоторое время цену на эту модель снизили до 15200 рублей. На сколько процентов была снижена цена? 4. (1 балл) На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
5. (1 балл) Найдите значение выражения log22 + log2 32
6.
(1 балл) Найдите корень уравнения ![]()
7. (1 балл) Решите неравенство 2х+5 > 64. В ответ запишите наименьшее положительное число.
8.
(1 балл) Найдите корень уравнения ![]()
9. (1 балл) Найдите производную функции в точке х=0: y=1,25х4-6х2 +7х-1
10. (1 балл) В цилиндрическую цистерну емкостью 12 т налито дизельное топливо. Сколько дизельного топлива содержится в цистерне, если ее высота равна 6 м, а уровень горючего 2 м?
11. ( 1 балл)Найдите площадь фигуры, изображенной на рисунке

12. (1 балл) Тело движется по закону S(t)=3t2+5t (м) Найдите скорость тела через 1с после начала движения.
При выполнении заданий 13-16 запишите ход решения и полученный ответ
13. (3 балла) Вычислите площадь верстака, отведенного для проведения работ технического обслуживания, периметр которого ограничивают линии у=x2-2x-2 и у=-x2+2.
Выполните чертеж. Ответ дайте в квадратных метрах.
14. (3
балла) Решите уравнение sin2x - 2sinx=0. В ответ запишите количество
решений, принадлежащих промежутку [0; 4 ] ![]()
15. (3 балла) Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

16. (3 балла) Ремонт одного и того же трактора Виктор и Алексей делают за 8 дней, как и Андрей вместе с Виктором, при этом Алексей с Андреем могут выполнить этот ремонт за 12 дней. Сколько дней длиться ремонт, если все три техника- механика будут работать одновременно?
Эталоны ответов:
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
Ответ |
2 |
3 |
5 |
0,25 |
6 |
-7 |
1 |
-10 |
7 |
35000 |
15 |
11 |
9 |
5 |
6 |
6 |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.