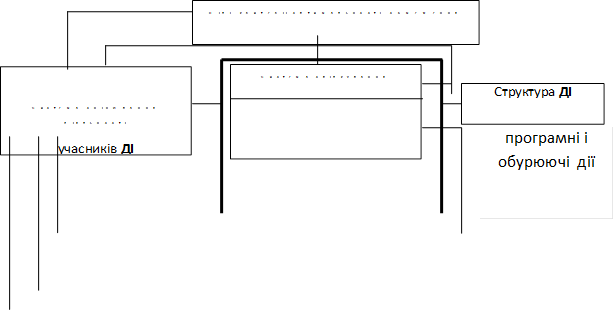
Функціональна схема ДІ

Функціональна схема ДІ

Приведені в попередньому питанні ознаки ДІ допомагають представити її функціональну схему.

                                                                  Ігровий комплекс

                                                                                                               рішення

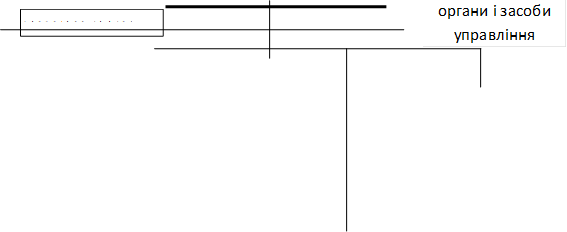
Рис. 1 – Функціональна схема ДІ.

Для організації і проведення ДІ необхідно:

1.      підготовка керівництва гри і групи забезпечення;

2.      підготовка методичного і технічного забезпечення;

3.      підготовка інструктивних завдань і пробного проведення гри з групою забезпечення;

4.      адаптація ДІ до відповідного контингенту учасників і умов її проведення;

5.      проведення необхідних розрахунків для оцінки наслідків різних варіантів рішень, формування оптимального або раціонального рішення для кожного фрагмента гри;

6.      попереднє формування складу ігрових груп;

7.      підготовка майбутніх учасників гри, оцінка рівня їх готовності.

3. Основні поняття, класифікація ігор.

Математична дисципліна, що досліджує ситуації, в яких ухвалення рішення залежить від декількох учасників, називають теорією ігор.

Предметом теорії ігор є такі ситуації, в яких важливу роль грають конфлікти і сумісні дії. Типовим прикладам подібних ситуацій може служити рекламування конкуруючих товарів.

У теорії ігор «особи, що ухвалюють рішення», називають гравцями, а цільову функцію – платіжною функцією.

Кожен гравець має в своєму розпорядженні кінцевий або нескінченний набір допустимих рішень, які називаються стратегіями. Відзначимо, що в теорії ігор поняття стратегії є одним з центральних.

Виграш кожного гравця визначається його платіжною функцією, значення якої залежать від стратегій всіх учасників гри.

Фактично,  гра є сукупність правил, відомих всім гравцям. Ці правила, з одного боку, визначають безліч стратегий гравців, а з іншої – наслідки і виграші в результаті вибору кожної із стратегій.

Класифікацію ігор проводять за різними ознаками:

1) по числу гравців;

2) по числу стратегій;

3) по властивостях платіжної функції;

4) по характеру попередній домовленості між гравцями.

5) по вигляду функцій виграшів;

6) по кількості ходів.

1) Гру, в якій бере  участь n- гравців, називають грою з n- учасниками. Кількість n учасників може бути рівною 2, 3 і т.д. За наявності 2-х гравців можуть виникати і конфліктні ситуації, і необхідність в координованих діях – кооперація.

Якщо в грі бере участь не менш 3-х гравців, то можуть створюватися коаліції, тобто групи з двох або більш за гравців, що мають загальну мету і координуючих свої стратегії.

2) По кількості стратегій розрізняють ігри кінцеві і нескінченні:

якщо хоч би один з гравців має в своєму розпорядженні нескінченний безліччю стратегій, то гру називають нескінченною;

якщо ж кожний з гравців має в своєму розпорядженні кінцеву безліч стратегій, то гру називають кінцевою.

3) Ще один спосіб класифікації ігор – по властивостях платіжної функції.

У грі з нульовою сумою загальна сума виграшів всіх гравців дорівнює нулю. У загальному випадку в грі з нульовою сумою, як правило, мають місце і конфлікти, і узгоджені дії гравців.

У грі з нульовою сумою і 2-ма учасниками виграш одного з них рівний програшу іншого. Таким чином, в іграх з нульовою сумою існує конфлікт між гравцями, і тому їх називають також антагоні-стічеськімі іграми.

Прямою протилежністю іграм з нульовою сумою є ігри двох гравців з постійною різницею, в яких обидва гравці виграють або програють одночасно. Тому гравцям вигідно діяти погоджено.

4) Залежно від характеру попередньої домовленості між ігроками розрізняють кооперативні і некооперативні ігри.

Гра кооперативна, якщо до її початку гравці утворюють коаліції і приймають взаємноузгоджуючі угоди про координацію своїх стратегій. Інакше гра буде некооперативною.

5) по вигляду функцій виграшів.

Ігри діляться на: матричні ігри

                            біматрічні ігри

                            безперервні ігри

                            опуклі ігри і ін.

Введемо ще два поняття, широко використовуваних в теорії ігор.

Хід – це момент гри, коли гравці повинні вибрати один з можливих варіантів дій, тобто прийняти одне з допустимих рішень.

Партія гри – це певна сукупність ходів і виборів можливих варіантів дій.

Тоді:

6) По кількості ходів гри діляться на:

однокрокові (що завершуються після одного ходу кожного з гравців)  і  багатокрокові, які, у свою чергу, діляться на

a)         позиційні ігри (кожний з гравців може послідовно в часі робити декілька ходів)

b)        стохастичні ігри (де при виборі нових позицій є певна вірогідність повернення на попередню позицію)

c)         диференціальні ігри (у яких допускається робити ходи безперервно і підпорядковувати поведінку гравців умовами, описуваними диференціальними рівняннями)

d)        ігри типу дуелей (що характеризуються моментом вибору ходу і вірогідністю отримання виграшів залежно від часу, що пройшов від початку гри до моменту вибору).