Инструкционная карта по дисциплине «Математика» Тема: Решение логарифмических уравнений и неравенств

КГУ «Риддерский многопрофильный колледж»

Инструкционная карта

по дисциплине «Математика»

Тема: Решение логарифмических уравнений и неравенств

Цель: Научиться вычислять логарифмические выражения.

Норма времени: 90 минут

Оснащение рабочего места: инструкционная карта, микрокалькулятор.

СОДЕРЖАНИЕ РАБОТЫ.

Задание 1. Решить логарифмические уравнения.

а)log ₂ (x + 8) = log ₂3 + log ₂5

6)

в)log ₂ (x + 1) = log ₂ (3x) 7) 

г)log ₅ (2x + 1) – log ₅ x = 0 

д)log ₂ (x – 1) = - 1

е)7 · 2 = 196

Методические указания

Ниже приведены основные формулы, которые надо знать, чтобы справиться с логарифмами:

1.  
2.  
3. log_a xⁿ = n · log_a x
4. 
5. 

Кроме того, надо уметь заменять корни и дроби на степени с рациональным показателем, иначе в некоторых выражениях выносить из под знака логарифма будет просто нечего. Формулы замены:

Из определения логарифма вытекают две формулы, которые постоянно встречаются в реальных задачах. Эти формулы позволяют заменить знак логарифма нормальными числами:

1.                 

2.                 

Задание 2. Решить логарифмическое неравенство.

 а)

б)

в)

г)

Методические указания

1.Неравенство   в случае, если  сводится к равносильному неравенству . Если же  - то к неравенству .

Аналогично неравенство   равносильно неравенствам для   : ;  для  : .

Решения полученных неравенств надо пересечь с ОДЗ: 

2.Решение логарифмического неравенства вида  равносильно решению следующих систем:

а) 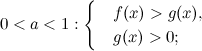      б)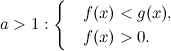 

Неравенство  в каждом из двух случаев сводится к одной из систем:

а) 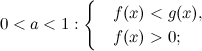      б)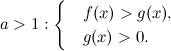 

Контрольные вопросы

1.Понятие логарифмического уравнения.

2. Показательное уравнение

Преподаватель: Синявская Анна Федоровна