ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА

Итоговая контрольная работа

В а р и а н т  1

1. Решите систему неравенств:

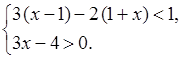
2. Упростите выражение: .

3. Упростите выражение: .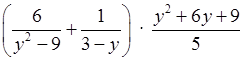

4. Два автомобиля выезжают одновременно из одного города в другой, находящийся на расстоянии 560 км. Скорость первого на 10 км/ч больше скорости второго, и поэтому первый приезжает на место на 1 ч раньше второго. Определите скорость каждого автомобиля.

5. При каких значениях х функция y = 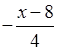 + 1 принимает положительные значения?

В а р и а н т  2

1. Решите систему неравенств:

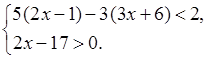
2. Упростите выражение: .

3. Упростите выражение: .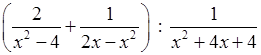

4. Пассажирский поезд был задержан в пути на 16 мин и нагнал опоздание на перегоне в 80 км, идя со скоростью, на 10 км/ч большей, чем полагалось по расписанию. Какова была скорость поезда по расписанию?

5. При каких значениях х функция y =  – 2 принимает отрицательные значения?

В а р и а н т  3

1. Решите неравенство: 4(2х – 1) – 3(3х + 2) > 1.

2. Упростите выражение: .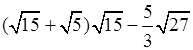

3. Упростите выражение: .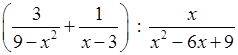

4. «Ракета» на подводных крыльях имеет скорость на 50 км/ч большую, чем скорость теплохода, и поэтому путь в 210 км она прошла на 7 ч 30 мин скорее, чем теплоход. Найдите скорость «Ракеты».

5. При каких значениях х функция y =  + 4 принимает отрицательные значения?

В а р и а н т  4

1. Решите неравенство: 9(х – 2) – 3(2х + 1) > 5х.

2. Упростите выражение: .

3. Упростите выражение: .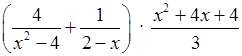

4. Из пункта А отправили по течению реки плот. Через 5 ч 20 мин вслед за ним вышла из пункта А моторная лодка, которая догнала плот на расстоянии 20 км от А. С какой скоростью двигался плот, если известно, что моторная лодка шла быстрее его на 12 км/ч?

5. При каких значениях х функция y = 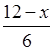 + 1 принимает положительные значения?

Решение вариантов контрольной работы

В а р и а н т  1

1.

   

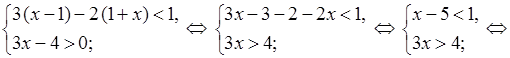
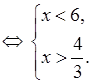
О т в е т: .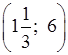

2.

    .

3. 1)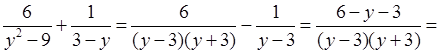

        ;

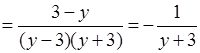2) .

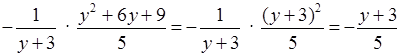О т в е т: .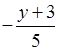

4. Пусть скорость первого автомобиля х км/ч, тогда скорость второго автомобиля (х – 10) км/ч.

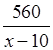Время, затраченное первым автомобилем на прохождение пути в 560 км, равно  ч, а время, затраченное вторым автомобилем на похождение этого же пути, равно  ч.

Первый автомобиль приезжает на место на 1 ч раньше второго. Получим уравнение:

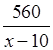 –  = 1.

Решим это уравнение:

560х – 560 (х – 10) = х (х – 10);

560х – 560х + 5600 = х² – 10х;

х² – 10х – 5600 = 0;

х₁ = –70 (не подходит по смыслу задачи);

х₂ = 80.

Получим, что скорость первого автомобиля равна 80 км/ч, а скорость второго 70 км/ч.

О т в е т: 80 км/ч и 70 км/ч.

5. Чтобы узнать все значения х, при которых функция y = 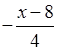 + 1 принимает положительные значения, нужно решить неравенство:

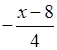 + 1 > 0;

 > –1;

8 – х > –4;

–х > –12;

х < 12.

О т в е т: при х < 12.

В а р и а н т  2

1.

   

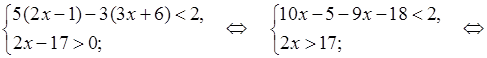
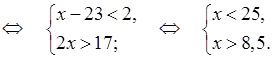
О т в е т: (8,5; 25).

2.

    .

3. 1)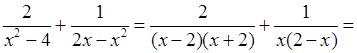

        .

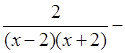
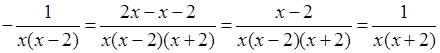2) .

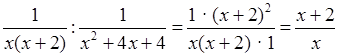О т в е т: .

4. Пусть х км/ч – скорость поезда по расписанию, тогда (х + 10) км/ч – его скорость на перегоне в 80 км. Если бы на перегоне в 80 км поезд шёл по расписанию, то он затратил бы на это  ч. В реальности этот перегон он преодолел за 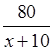 ч. Отрезок пути, равный 80 км, поезд в реальности прошёл на 16 мин (или  ч) быстрее, чем предполагал по расписанию.

Получим уравнение:

 –  = .

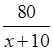Решим это уравнение:

15 · 80(х + 10) – 15 · 80х = 4х(х + 10);

15 · 80х + 15 · 80 · 10 – 15 · 80х = 4х² + 40х;

4х² + 40х – 15 · 80 · 10 = 0;

х² + 10х – 3000 = 0;

х₁ = –60 (не подходит по смыслу задачи);

х₂ = 50.

О т в е т: 50 км/ч.

5.  – 2 < 0;

    6 – х – 10 < 0;

    – х < 4;

    х > –4.

О т в е т: х > –4.

В а р и а н т  3

1. 4(2х – 1) – 3(3х + 2) > 1;

    8х – 4 – 9х – 6 > 1;

    –х > 11;

    х < –11.

О т в е т: (–∞; –11).

2.

    .

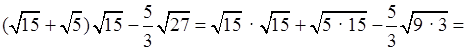
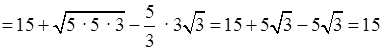3. 1)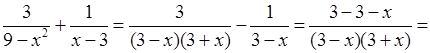  

         ;

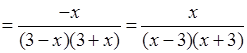2) .

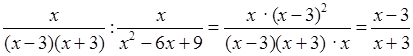О т в е т: .

4. Пусть скорость «Ракеты» х км/ч, тогда скорость теплохода (х – 50) км/ч. Путь в 210 км «Ракета» проходит за  ч, а теплоход – за 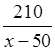 ч. По условию этот путь «Ракета» проходит быстрее теплохода на 7,5 ч.

Получим уравнение:

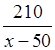 –  = 7,5.

Решим это уравнение:

210х – 210 (х – 50) = 7,5х(х – 50);

210х – 210х + 210 · 50 = 7,5х² – 7,5 · 50х;

7,5х² – 7,5 · 50х – 210 · 50 = 0;

15х² – 15 · 50х – 210 · 100 = 0;

х² – 50х – 1400 = 0;

х₁ = –20 (не подходит по смыслу задачи);

х₂ = 70.

О т в е т: 70 км/ч.

5.  + 4 < 0;

    х – 3 + 12 < 0;

    х < –9.

О т в е т: х < –9.

В а р и а н т  4

1. 9(х – 2) – 3(2х + 1) > 5х;

    9х – 18 – 6х – 3 > 5х;

    3х – 5х > 21;

    –2х > 21;

    х < – 10,5.

О т в е т: (–∞; –10,5).

2.

    .

3. 1)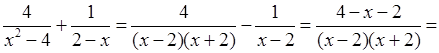

          ;

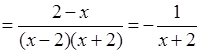2) .

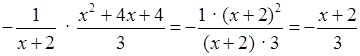О т в е т: .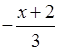

4. Пусть х км/ч – скорость течения реки, тогда моторная лодка шла со скоростью (12 + х) км/ч. Расстояние в 20 км плот прошёл за  ч, а моторная лодка – за 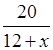 ч. Лодка была в пути на 5 ч меньше, чем плот.

Получим уравнение:

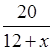 –  = 5.

Решим это уравнение:

;

;

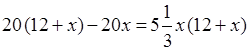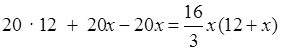60 · 12 = 16х (12 + х);

15 · 3 = х (12 + х);

х² + 12х – 45 = 0;

х₁ = –15 (не подходит по смыслу задачи);

х₂ = 3.

О т в е т: 3 км/ч.

5. 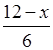 + 1 > 0;

    12 – х + 6 > 0;

    –х > –18;

    х < 18.

О т в е т: х < 18.

 

 

Литература

1. Алгебра : учеб. для 8 кл. общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова ; под ред. С. А. Теляковского. – М. : Просвещение, 2009.

2. Макарычев. Ю. Н.  Дидактические  материалы по алгебре для 8 класса / Ю. Н. Макарычев, Н. Г. Миндюк, Л. М. Короткова. – М. : Просвещение, 2008.

3. Математические диктанты для 5–9 классов : кн. для учителя / Е. Б. Арутюнян, М. Б. Волович, Ю. А. Глазков, Г. Г. Левитас. – М. : Просвещение, 1991. – 80 с.

4. Решение задач по статистике, комбинаторике и теории вероятностей. 7–9 классы  /  авт.-сост.  В. Н. Студенецкая.  –  2 изд.,  испр.  –  Волго-град : Учитель, 2006. – 428 с.

5. Ткачева, М. В. Элементы стохастики в курсе математики 7–9 классов основной школы / М. В. Ткачева, Н. Е. Федорова // Математика в школе. – 2003. – № 3. – С. 36–50.

 

 

Скачано с www.znanio.ru