Итоговая контрольная работа 7

Итоговая контрольная работа

Демоверсия

№ 1. В треугольнике CDE известно, что ∠C = 30°, ∠E = 83°. Укажите верное неравенство: 1) DE > CD; 2) CD > CE; 3) CE > DE; 4) DE > CE.

№ 2. Докажите, что AC = BD (рис. 71), если AО = ОC и ∠DAС = ∠CBD.(О- точка пересечения отрезковAC и BD)

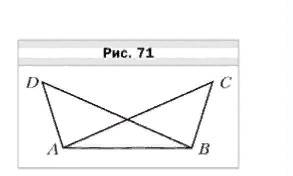
№ 3. В треугольнике ABC известно, что ∠A = 80°, ∠B = 40°. Биссектриса угла A пересекает сторону BC в точке M. Найдите угол AMC.

№ 4. Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 3:8, считая от вершины угла при основании треугольника. Найдите стороны треугольника, если его периметр равен 190 см.

Вариант 1

№ 1. В треугольнике CDE известно, что ∠C = 28°, ∠E = 72°. Укажите верное неравенство: 1) DE > CD; 2) CD > CE; 3) CE > DE; 4) DE > CE.

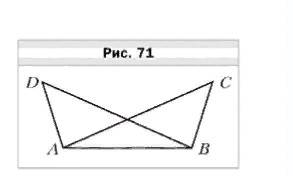
№ 2. Докажите, что AC = BD (рис. 70), если AD = BC и ∠DAB = ∠CBA.

№ 3. В треугольнике ABC известно, что ∠A = 70°, ∠B = 50°. Биссектриса угла A пересекает сторону BC в точке M. Найдите угол AMC.

№ 4. Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 2:7, считая от вершины угла при основании треугольника. Найдите стороны треугольника, если его периметр равен 110 см.

Вариант 2

№ 1. В треугольнике CDE известно, что ∠C = 55°, ∠D = 110°. Укажите верное неравенство: 1) CE < CD; 2) CE < DE; 3) DE < CD; 4) CD < DE.

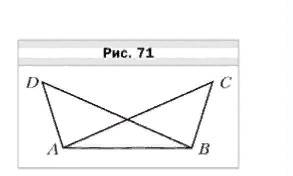
№ 2. Докажите, что ∠ACB = ∠BDA (рис. 71), если AD = BC и ∠BAD = ∠ABC

№ 3. В треугольнике MNK известно, что ∠N = 50°. Биссектриса угла N пересекает сторону MK в точке F, ∠MFN = 74°. Найдите угол MKN.

№ 4. Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 4:5, считая от вершины угла при основании треугольника. Найдите стороны треугольника, если его периметр равен 104 см.

Критерии оценивания