Итоговая КР за курс алгебры 8 класса

Таблица количества баллов за выполнение задания

Максимальное количество баллов за 1 задание			Количество баллов за работу в целом
Часть 1	Часть 2
задания 1-8	задания 9-11	задания 12-13
1 балл	2 балла	3 балла	20 баллов

Таблица перевода тестовых баллов в школьные отметки

Тестовый балл	Школьная отметка
7-10	«3»
11-14	«4»
15-20	«5»

Ответы на итоговую аттестацию по алгебре в 8 классе:

13.1. Второй ехал со скоростью x, значит первый: x + 4. Всю дорогу первый прошел за 96/(x+4) часа, а второй за 96/x часа. Значит: 4 + 96/(x+4) = 96/x

X² + 28x = 24x + 96

X² + 4x - 96 = 0

D = 4 + 96 = 100

x = -2 +-10 = -12 или 8

-12 не удовлетворяет, так как скорость не может быть минусовой.

Значит скорость второго: 8 км/ч, он же и пришел к финишу на 4 часа позже первого, значит:

Ответ: 8км/ч

13.2. Пусть скорость второго велосипедиста x км/ ч. Он ехал 130 / x часов.

Скорость первого велосипедиста (x + 3) км/ч. Он ехал 130 / (x + 3) часов.

Разница 130 / x - 130 / ( x + 3) = 3;

130 * (x + 3) - 130 x = 3x * (x +3);

130x + 390 – 130x = 3x² + 9x;

3x² + 9x – 390 = 0;

x² + 3x – 130 = 0;

D = 3² – 4 * (-130 * 1) = 9 + 520 = 529 =23²;

x1 = -3 - 23 / 2 <  0 – не удовлетворяет условию задачи;

x2 = -3 + 23 / 2 = 10.

Значит, скорость второго велосипедиста 10 км/ч.

Ответ: 10 км/ч.

 

Итоговая контрольная работа по алгебре за 8 класс

Вариант 1

 Часть 1

1. Найти значение выражения +0,09

2. Выберите неверное равенство:

1)

                                                                                 

3. Установите соответствие между графиками функций и формулами, которые их задают.

А)

Б)

В) б

Г)

 

1) у=2х           2) у=-2х            3) у=х+2             4) у=2              5) у = х²

 

А	Б	В	Г

 

 

 

4. Упростите выражение         

 1);       2)10;         3);       4)2.

 

5. Решите уравнение  х²+3х-4=0.Найдите среднее арифметическое корней.

 

 1)1.   2) -1,5.  3) -3.          4) нет корней.

 

6. Решите систему уравнений: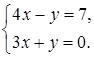

1) (- 3; 1);   2) (3; 1);      3) (1; - 3);   4) (- 1; - 3).

 

7. Решить неравенство  и выбрать, на каком рисунке изображено множество его решений.

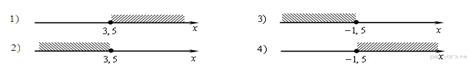
8. Решите систему неравенств: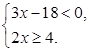

 

 

Часть 2. (запишите полное решение и ответ)

 

9. Найдите отрицательный корень уравнения 2х²-72=0

10. Решите уравнение: .     

11. Найти значения а, при которых уравнение  не имеет корней

 

12. Решите систему уравнений: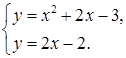  

 

13. Два велосипедиста одновременно отправились в 96-километровый пробег. Первый ехал со скоростью, на 4 км/ч большей, чем скорость второго, и прибыл к финишу на 4 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым.

Итоговая контрольная работа по алгебре за 8 класс.

 Вариант 2.  

Часть 1.

1. Найти значение выражения   0,08+

2. Выберите неверное равенство:

1)

 

А)

Б)

В)

Г)

3.Установите соответствие между графиками функций и формулами, которые их задают

1) у =           2) у = | х |           3) у=х+2             4) у=2          5) у = х²    

А	Б	В	Г

 

 

 

 

4.  Упростите выражение   

 

1)1;      2);           3);       4)2.

 

5. Решите уравнение  х²-7х+10=0. Найдите  среднее арифметическое корней.

  1) -3,5        2) 2       3) 3,5      4) нет корней

 

6.  Решите систему уравнений: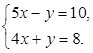     

      1) ( 2; 1);      2) (2; 0);          3) (1;  2) ;             4) (1; 2).

 

7.  Решить неравенство  

1) (− ∞; 8)         2) (− ∞;1).        3) (8; +∞).    4) (1; +∞)

 

8.  Решите систему неравенств:

 

 

 

 

Часть 2.

  9.  Найдите отрицательный корень уравнения 2х² -50=0

 

10. Решите уравнение: .

 

11. Найти значения а, при которых уравнение  имеет два различных корня.

 12. Решите систему уравнений: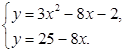

13. Два велосипедиста одновременно отправились в 130-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым.