Конспект по физике на тему "Закон всемирного тяготения"

Закон всемирного тяготения

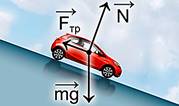
Из законов динамики нам хорошо известно, что для того, чтобы тело двигалось ускоренно, на него должна действовать сила, как в данном примере с автомобилем на рис. 1. Равнодействующая направлена таким образом, что машина ускоряется.

Рис. 1. Иллюстрация действий сил на тело

В то же время мы хорошо знаем, что земля сообщает одинаковое ускорение любым падающим на нее телам. Эту силу, с которой действует земля на падающие тела, мы традиционно называем сила тяжести. На рис. 2 проиллюстрировано действие силы тяжести.

Рис. 2. Иллюстрация действия силы тяжести

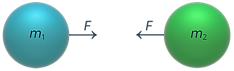
В конце XVII века Исаак Ньютон, которому на тот момент было всего 22 года, предположил, что свойство притягивать тела характерно не только для земли, но и для любых тел, обладающих массами (рисунок 3). Такую силу он назвал силой всемирного тяготения, а взаимодействие, ответственное за появление этой силы, было названо гравитационным (от латинского gravitas – «тяжесть»).

Рис. 3. Взаимодействие двух тел обладающих массой

Формулировка закона

Закон всемирного тяготения позволяет описывать не только падение тел на землю, но и движение планет, звезд, приливы, отливы и множество других универсальных явлений, которые протекают в природе. Попробуем восстановить ход рассуждений Ньютона, а он получил математическую формулу, описывая движение Луны вокруг Земли, и тоже получить закон всемирного тяготения.

Если Земля сообщает любому телу, находящемуся на ее поверхности, ускорение свободного падения g, которое, как мы знаем, по модулю равно g = 9,8 , то Луне притяжение Земли сообщает центростремительное ускорение. Запишем некоторые характеристики.

Радиус Земли (он нам понадобится в расчетах) R₃ = 6370 км, орбиты Луны R_Л = 384000 км, период обращения Луны вокруг Земли, так называемый лунный месяц Т = 27,3 суток.

Ньютон предположил, что сила, с которой Земля притягивает те или иные объекты, зависит от расстояния между объектом и центром Земли. Известно, что расстояние от Луны до центра Земли примерно в 60 раз больше чем радиус Земли, т. е. расстояние от любого тела находящегося на поверхности Земли.

Закон всемирного тяготения: тела притягиваются друг к другу с силой, модуль которой пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними. Сила направлена вдоль прямой, соединяющей центры тел.

Математическая запись этой формулы:

Как Луна влияет на Землю

Несмотря на то, что Луна расположена от Земли достаточно далеко, расстояние составляет порядка 400 000 км, ее влияние на Землю все-таки весьма ощутимо. Итак, поговорим о том, как Луна влияет на вес тел, находящихся на Земле. Сразу оговоримся: мы не будем учитывать влияние Солнца и других небесных тел, так как оно по сравнению с влиянием Луны значительно меньше.

Если подсчитать, воспользовавшись законом всемирного тяготения, влияние Луны на вес тел на Земле, то окажется что в наиболее близкой к Луне и в наиболее удаленной от Луны точках земной поверхности вес тела несколько уменьшается, а в точке, лежащей на средней линии, вес тела немного увеличивается. При этом изменение веса, показанное на рисунке 4 красным цветом, в два раза меньше, чем изменение веса, показанное на рисунке 5 также красным цветом, для точек наиболее близкой и наиболее удаленной.

Если бы Луны вообще не было на земной орбите, то вес тела уменьшился бы совершенно незначительно. Если перейти от ньютонов к единицам ускорения , то эта величина составляла бы всего лишь 0,0001 . По сравнению, например, с ускорением свободного падения 10  (мы здесь его округлили от 9,8 до 10), вы видите, что разница составляет порядка одной стомиллионной доли. Немного? Да, немного, но если сравнивать с радиусом Земли те изменения, которые привносит такое небольшое измерение ускорения в результате отсутствия Луны, то мы получим, что Rз = 6400 км. И эти стомиллионные доли изменения приводят к тому, что высота уровня воды в точках, показанных на рис. 4, поднимается на 54 см, в точках, показанных на рис. 5, она падает на 27 см (см. рис. 3).

Речь идет о явлении приливов и отливов. Именно Луна определяет наличие приливов и отливов на Земле.

Благодаря вращению Земли места подъемов и опусканий уровня воды постоянно перемещаются. Именно такие постоянные перемещения мы и ощущаем в виде приливов и отливов. Конечно же, приливы и отливы зависят и от географического места на Земле, например, на Черном море или на Каспийском море приливы практически не наблюдаются, однако в Охотском море есть бухта, в которой высота приливных волн достигает нескольких метров.

Еще одно интересное влияние Луны на Землю – в результате приливов и отливов, волна, которая бежит вдоль земли трется о поверхность земли и, значит, несколько замедляет вращение Земли. Интересно, что тот факт, что мы всегда видим Луну повернутой к нам одним боком, тоже предопределил теперь уже влияние Земли на Луну.

Границы применимости

А сейчас поговорим об ограничениях, о границах применимости той формулировки закона всемирного тяготения, которую мы записали. В каких случаях он справедлив? К примеру, есть два тела А и В. Они, согласно закону всемирного тяготения, притягиваются друг к другу. Если эти тела притягиваются и, например, находятся на расстоянии, показанном на рисунке 6, то какую величину брать в качестве r (расстояния между ними) – либо самое маленькое между ними, либо расстояние между наиболее дальними краями, или же расстояние между серединками? А где взять эту серединку? Итак, возникает вопрос: применима ли формула закона всемирного тяготения для тел неправильной формы, находящихся на таком расстоянии друг от друга?

Рис. 6. Положение тел А и В

Ответ мы можем получить, для этого увеличим расстояние между телами. Когда мы их разнесли достаточно далеко друг от друга, нужно ли учитывать их размеры? Нет, ведь их размеры по сравнению с расстоянием между ними очень малы, поэтому в данном случаи мы их можем полагать материальными точками. Итак, первое ограничение:

1. Закон всемирного тяготения применим для тел, размеры которых несущественны по сравнению с расстоянием между ними. Такие тела мы называем материальными точками. Это первое условие.

Однако есть ситуации, когда можно рассматривать тела, обладающие реальными размерами и находящиеся на небольшом расстоянии друг от друга. Это тела примерно такой формы, как показано на рисунке 7.

Рис. 7. Положение тел сферической формы

Представьте себе, что это идеальные сферы. Если тела, обладающие сферической формой, или, говорят, сферической симметрией, находятся даже на небольшом расстоянии друг от друга, мы можем пользоваться формулой закона всемирного тяготения в качестве расстояния r. В этом случае мы берем расстояние между центрами тел, именно в такой форме мы пользуемся законом всемирного тяготения, когда рассматриваем наше притяжение к центру Земли.

Второе условие, при котором можно применять закон всемирного тяготения в той форме, которую мы записали:

2. Тела должны обладать сферической симметрией.

Гравитационная постоянная

Поняв, в каких случаях можно применять формулу для закона всемирного тяготения, вернемся к величине G (коэффициенту пропорциональности):

Эта величина носит название гравитационной постоянной. Выясним какой смысл у гравитационной постоянной G. Запишем еще раз закон всемирного тяготения:

Отсюда несложно получить, что гравитационная постоянная G может быть вычислена по формуле:

Итак, отсюда мы получаем физический смысл гравитационной постоянной. В самом деле, если мы возьмем две материальные точки, расположенные на расстоянии 1 м друг от друга, а масса этих материальных точек равна 1 кг, то гравитационная постоянная будет численно равна силе, с которой притягиваются эти две точки. Физический смысл гравитационной постоянной: она численно равна силе, с которой мысленно притягиваются две материальные точки массами по 1 кг, расположенные в вакууме на расстоянии 1 м друг от друга. 

Эта величина и носит название гравитационной постоянной и является так называемой универсальной физической постоянной, т. е. одинаковой в любой точке Вселенной.

Выводы

1.                  Взаимодействие, свойственное всем телам во Вселенной и проявляющееся в их взаимном притяжении друг к другу, называют гравитационным, а само явление – всемирным тяготением или гравитацией.

2.                  Закон всемирного тяготения имеет следующий вид: 

Сила взаимодействия между двумя телами массами , находящимися на расстоянии  друг от друга, прямо пропорционально произведению масс этих тел и обратно пропорционально квадрату расстояния между ними.

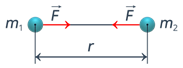
Направление силы вдоль прямой, соединяющей центры тел, представлено на рисунке 10.

Рис. 10. Направление силы вдоль прямой, соединяющей центры тел

3. Справедлив этот закон в таком виде для:

·                     если тела можно положить материальными точками, т. е. их размерами можно пренебречь по сравнению с расстоянием между телами;

·                     если тела обладают сферической симметрией.

Скачано с www.znanio.ru