Математический аппарат физики

Вектора не всегда расположены «удобно» и производить вышеперечисленные действия с ними бывает трудоёмко. Поэтому действия с векторами сводят к действиям с положительными и отрицательными числами – проекциями векторов.

Проекция вектора на ось. Проекцией вектора 𝑎⃗ на ось 𝑥 называется длина отрезка 𝑎_$ между проекциями на эту ось начала и конца вектора.

Если проекция вектора на ось совпадает положительным направлением оси, то она положительна, в противном случае – отрицательна

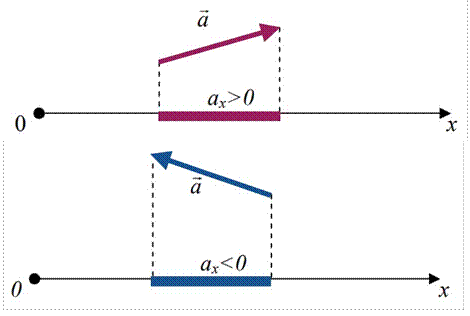
Если вектор перпендикулярен оси, то его проекция равна 0.

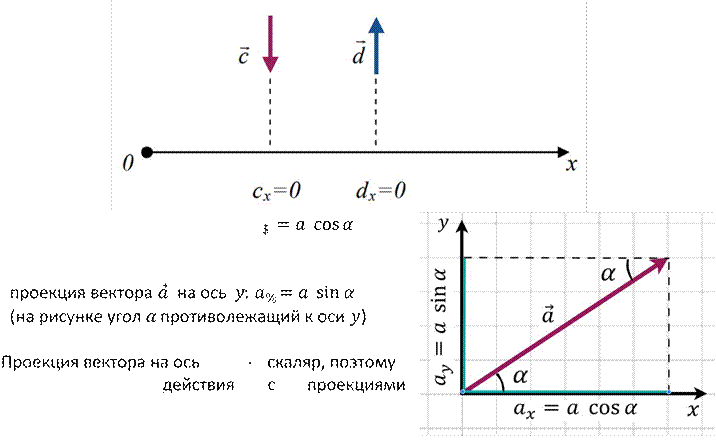проекция вектора 𝑎⃗  на ось  х: 𝑎

(на рисунке угол 𝛼 прилежащий к оси 𝑥)

математические производятся алгебраически.

Основные понятия механики

Механика — это раздел физики, изучающий механическое движение тел.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение (не рассматриваются силы).

Механическое движение - изменение положения тела в пространстве относительно других тел с течением времени. 

Механическое движение может быть:

1. По характеру движения

•   поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;

•   вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;

•   колебательным — это движение, которое повторяется с течением времени.

2. По виду траектории

•   прямолинейным — это движение, траектория которого прямая линия;

•   криволинейным — это движение, траектория которого кривая линия;

3. По скорости

•   равномерным — движение, при котором скорость тела с течением времени остается постоянной;

•   неравномерным — это движение, при котором скорость тела с течением времени изменяется; 4. По ускорению

•   равноускоренным — это движение, при котором скорость за любые равные промежутки времени тела увеличивается с течением времени на одну и ту же величину; • равнозамедленным — это движение, при котором скорость тела за любые равные промежутки времени уменьшается с течением времени на одну и ту же величину

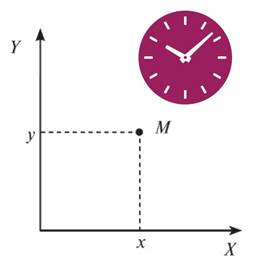
Система       отсчёта         служит          для     количественного описания механического      движения. Поэтому вследствие определения механического движения систему отсчёта образуют:

1.        тело отсчёта (не меняющее своей формы); 2.    система координат, жёстко связанная с телом отсчёта;

3.        часы (прибор для измерения времени), жёстко связанные с телом отсчёта.

Модель тела, собственными размерами которого в условиях данной задачи можно пренебречь, называют материальной точкой. Тело можно считать материальной точкой, если:

•   расстояние, которое проходит тело, много больше его размера; • расстояние от данного тела до другого тела много больше его размера;

•   тело движется поступательно (не вращается).

Материальная точка — это модель реальных объектов, реальных тел. Считая тело материальной точкой, мы отвлекаемся от несущественных для решения конкретной задачи признаков, в частности от размеров тела.

Траектория — это линия, которую описывает тело при своем движении.

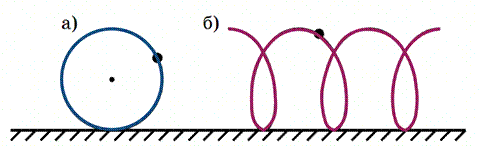
Движение тел может выглядеть по-разному для различных наблюдателей. В этом заключается относительность механического движения. Траектория движения тела относительна: её форма зависит от выбора системы отсчёта. Так, траекторией точек обода колеса велосипеда, движущегося по прямой дороге, относительно оси колеса является окружность (а), а относительно Земли — винтовая линия (б). 

Путь (𝑙) — это скалярная величина, равная длине траектории.

Путь обозначают буквой (𝑙 (иногда 𝑠), основная единица пути 1 м: [𝑙] = 1м. Кратная единица пути — километр (1 км = 1000 м); дольные единицы — дециметр (1 дм = 0,1 м), сантиметр (1 см = 0,01 м) и миллиметр (1мм = 0,001 м).

Путь является скалярной величиной, то есть не имеющей направления. 

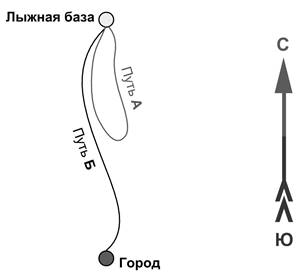Однако для решения практических задач недостаточно знать только путь. Например, из лыжной базы в 15 км к северу от города вышел лыжник и за 2 ч прошел 15 км. Как определить, куда он пришел? Он мог дойти до города - путь Б, а мог и вернуться обратно - путь А. В любом случае путь будет равен 15 км, но положение в пространстве будет разным. 

Чтобы избежать такой неопределенности, вводится понятие перемещения.

Перемещение (𝑠⃗) — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени. Перемещение — векторная физическая величина имеет направление и числовое значение.

Единица перемещения [s] = 1 м

В том случае, когда вектор перемещения лыжника был направлен на юг, то модуль перемещения равен 15 км, и мы можем сказать, что лыжник дошел до города. А в случае, когда лыжник пришел обратно на базу, его перемещение равно нулю.

Обрати внимание!

В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.

При    прямолинейном движении   в          одном           направлении         путь    равен модулю перемещения, а при криволинейном — путь больше перемещения. Перемещение на замкнутой траектории равно нулю.  

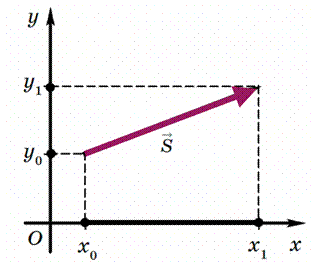При решении задач пользуются проекциями вектора перемещения.      На       рисунке  изображены система координат и вектор перемещения в этой системе координат.

Координаты начала перемещения — 𝑥_&, 𝑦_&; координаты конца перемещения — 𝑥_!, 𝑦_!. Проекция вектора перемещения на ось ОХ равна:           𝑠_$        = 𝑥_!–  𝑥_&.      Проекция    вектора перемещения на ось ОY равна: 𝑠_%   = 𝑦_!– 𝑦_&.

Модуль вектора перемещения равен: 𝑠 =

I𝑠$" + 𝑠%"