Конспект урока алгебры в 8 классе по теме_ «Решение систем неравенств с одной переменной»

8 класс                                              Алгебра                                Дата________________                      
 Урок № ___

Тема: Решение систем неравенств с одной переменной.

Тип: урок изучения нового материала.

Основные дидактические цели и задачи урока: изучить понятие решения системы неравенств с одной переменной; получить и закрепить навык решения систем неравенств с одной переменной.

ХОД УРОКА

I. Организационный момент

Учитель и ученики приветствуют друг друга. Проверяется готовность к уроку. Выявление отсутствующих на уроке.

II. Проверка домашнего задания

Учитель берёт тетради для проверки выполнения домашнего задания у 2–3 учащихся.

III. Актуализация опорных знаний учащихся

– Какую тему мы проходили на прошлом уроке?
– Уверены ли вы, что до конца научились решать неравенства с одной переменной?
– Сейчас мы это и проверим. А сделаем мы это с помощью самостоятельной работы, которую вы должны будете выполнить в течении 3–5 минут.

Ученики достают двойные листочки, на которых они будут выполнять самостоятельную работу. Учитель раздаёт карточки с заданиями:

IV. Изучение нового материала

1. Рассмотрим задачу:
Боковая сторона равнобедренного треугольника равна 3 см, а его периметр больше 8 см. Какую длину может иметь основание треугольника.

Решение
Пусть основание – х см. Значение х должно удовлетворять нескольким условиям:
1) Периметр должен быть больше 8 см. Получаем неравенство 3 + 3 + х > 8, которое поле упрощения принимает вид 6 + х > 8.
2) Должно выполняться равенство треугольника (каждая сторона треугольника должна быть меньше суммы двух других сторон), т.е. х < 3 + 3, что означает х<6.

Требуется найти те значения х, при которых верны неравенства 6 + х > 8 и х<6. Нам надо найти общее решение этих неравенств. В таких случаях говорят, что надо решить систему неравенств, и используют запись с фигурной скобкой. Запишем получившуюся систему неравенств: .

В первом неравенстве перенесём число 6 направо: , и после упрощения получим систему: . Значит х должно удовлетворять условию 2 < х < 6. Получили, что основание треугольника больше 2 см, но меньше 6 см. Мы нашли решение системы неравенств.

Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое неравенство системы.

В задаче, которую мы рассмотрели, решение системы
удовлетворяет двойному неравенству 2 < х < 6. Если
изобразить его на числовой прямой, то ответ можно
записать в виде интервала (2; 6).

2. Решим систему методом последовательного упрощения неравенств.

1) Раскроим скобки:

2) Перенесём слагаемые с переменными налево, а слагаемые без переменных направо, не забывая при переносе менять знак слагаемого: .

3) После приведения подобных слагаемых получим: .

4) Разделив обе части первого неравенства на -2, а обе части второго неравенства на 7, получим: .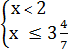

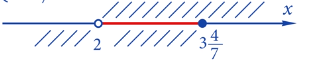Изобразим решение каждого неравенства
на одном чертеже. Для этого воспользуемся
 геометрическими моделями каждого числового
промежутка. Найдём пересечение, полученных числовых множеств. Запишем ответ в виде промежутка.

Ответ: (2; 3].

V. Закрепление изученного материала. Решение упражнений

1. Решение упражнений из учебника

№ 875 – решатся устно
№ 876 – решают два ученика возле доски, а остальные – в тетради.
№ 878 – два учащихся, сидя за партой, решают и диктуют остальным учащимся решение.
№ 879 – решают два ученика возле доски, а остальные – в тетради.

2. Решение упражнений из доп. литературы

1) Решите системы неравенств
а) ;             б) .
2)  Решите неравенство |12 + y| < 5.

VI. Рефлексия учебной деятельности

– Что такое решение системы неравенств с одной переменной?
– Понадобятся ли нам решения систем неравенств с одной переменной при решении геометрических задач? А при решении бытовых задач?

VII. Домашнее задание

·        Прочитать п. 35

·        Решить № 874, 877

VIII. Подведение итогов урока

Учитель выставляет оценки учащимся за работу на уроке, тем самым подводит итоги урока.