Конспект урока Коллинеарные и компланарные векторы

Заплани-

рованные этапы урока, время

Деятельность, запланированная на уроке

Ресурсы

Начало урока

Орг. момент.

Проверка домашнего задания.

Вопросы для повторения

1.       Что называют вектором?

2.       Выполняется ли правило параллелограмма и правило треугольника в случае сложения векторов в пространстве?

3.       Сформулируйте правило параллелепипеда для сложения векторов в пространстве?

4.       Какие векторы называются равными?

5.       Какие векторы называются сонаправленными в пространстве; противоположно направленными в пространстве?

Презентация

Середина урока

https://drive.google.com/file/d/1SpAuXqH38NmLBI6T8KP_uBqVQhuR2PID/view?usp=sharing

http://school-collection.edu.ru/catalog/res/3208b518-f002-4c6a-a8ce-210e81e71261/view/

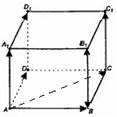
Определение

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны; три вектора, среди которых два коллинеарные, также компланарны.

Пример: рис. 1.

На рис. 1 изображен параллелепипед.

Векторы  - компланарны, так как, если отложить от точки О вектор, равный  то получится вектор  а векторы  лежат в плоскости ОСЕ.  - некомпланарны, так как вектор  не лежит в плоскости ОАВ. Признак компланарности 3-х векторов: если вектор  можно разложить по векторам  то есть представить в виде:  (х, у - некоторые числа), то векторы  - компланарны.

Доказательство: Пусть  не коллинеарные (рис. 2) (если коллинеарные - компланарность очевидна). Отложим отточки О векторы:  и  лежат в плоскости ОАВ. В плоскости ОАВ лежат и векторы  и  лежит в той же плоскости.  Что и требовалось доказать. Обратное утверждение: если векторы  компланарны, а векторы  некомпланарны, то вектор  можно разложить по векторам  то есть  причем коэффициенты х и у определяются единственным образом.

Ads by optAd360

Доказательство: (самостоятельно) на основании теоремы о разложении вектора по двум неколлинеарным векторам.

1)  - компланарны (по условию).

Если их отложить от точки А, то они будут лежать в одной плоскости.

2) Построим параллелограмм ABCD: 

3)  коллинеарные  аналогично 

4)  что и требовалось доказать (единственность коэффициентов х, у доказать самостоятельно дома).

Правило параллелепипеда (для сложения трех некомпланарных векторов).

Дано:  (рис. 3).

Ссылка 1, 2

Презентация к уроку.

Закрепление.

Закрепление нового материала.

Пример 1.

Дано:  (рис. 4).

1) Доказательство: 

2)  - компланарны - ?

согласно признаку компланарности, векторы  компланарны.

Презентация

Конец урока

Рефлексия

Слайд

Домашнее задание:

1.      Написать конспект.

2.      Решить задачу.

3.      Составить вопросы к лекции.

Карточка-задание

№

Выполненное задание:

Баллы

1.       

Составить конспект.

30

2.       

Решить задачу.

40

3.       

Составить вопросы к лекции.

30