
КГУ «Индустриально-технологический колледж»
Поурочный план № 149-150
Понятие многогранника. Призма и ее элементы, виды призм. Развертка, площадь боковой и полной поверхности призмы.
(тема занятия)
Наименование
дисциплины: Математика
Подготовил педагог: Тихоненко С.А.
Дата урока: 26.04.2021 года
1. Общие сведения
1.1 Курс, группы: первый, 9СЛ20, 9МК20, 9ОП20
1.2 Тип занятия: комбинированный/ дистанционный
1.3 Межпредметные связи: физика, черчение.
2. Цели, задачи:
Образовательные цели: сформировать представления об основных элементах пространственной геометрической фигуры - призмы, их основных свойствах; сформировать умения распознавать на чертежах, моделях и в реальном мире многогранные геометрические фигуры; способствовать формированию умения организовывать собственную деятельность, выбирать типовые методы и способы выполнения упражнений.
Воспитательные цели: развивать коммуникативные способности; создавать условия для развития скорости восприятия и переработки информации, культуры речи; формировать умение работать в коллективе и команде.
Развивающие цели: способствовать выработке навыков выполнения упражнений на построение прямых и наклонных призм.
способствовать формированию и развитию культуры учащихся, повышению уровня познавательного интереса к предмету.
2.2 Результаты обучения:
1) Усвоить понятие многогранник.
2) Решать задачи на нахождение элементов многогранников, площади поверхности.
2.3 Критерии оценки:
1) Раскрывает содержание понятия многогранника и его элементов;
2) Объясняет свойства многогранников по видам.
3) Изображает многогранники и выполняет их развёртки;
4) Определяет виды правильных многогранников;
5) Решает задачи на нахождение элементов многогранников;
6) Применяет формулы площади боковой и полной поверхности многогранников при решении задач.
3. Оснащение занятия
3.1 Учебно-методическое оснащение: дидактические материалы, справочно-инструктивные таблицы, карточки с заданиями, оценочные листы.
Справочная литература: А.Е.Әбылқасымова, В.Е. Корчевский, З.Ә. Жумагулова, Алгебра и начала анализа: Учебник для 10 классов естественно- математического направления обшеобразовательных школ.1-2 часть. Алматы: Мектеп, 2019г.
3.2 Техническое оснащение, материалы, ИКТ: мультимедийный проектор, ноутбук, экран.
4. Ход занятия
|
Заплани- рованные этапы урока, время |
Деятельность, запланированная на уроке
|
Ресурсы
|
|
Начало урока |
Орг. момент. |
|
|
|
Проверка домашнего задания. Вводная беседа по теме «Многогранники». |
Презентация
|
|
Середина урока |
https://drive.google.com/file/d/1SpAuXqH38NmLBI6T8KP_uBqVQhuR2PID/view?usp=sharing
http://school-collection.edu.ru/catalog/res/3208b518-f002-4c6a-a8ce-210e81e71261/view/
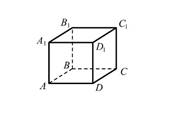
Многогранник — это тело, ограниченное конечным числом плоскостей. Эти плоскости, пересекаясь, образуют грани многогранника — многоугольники. Стороны этих многоугольников называются рёбрами многогранника, а концы рёбер — его вершинами. Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами. На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.
Элементы призмы Для рисунка выше: · Основания – равные многоугольники. Это могут быть треугольники, четырех-, пяти-, шестиугольники и т.д. В нашем случае – это параллелограммы (или прямоугольники) ABCD и A1B1C1D1. · Боковые грани – это параллелограммы: AA1B1B, BB1C1C, CC1D1D и AA1D1D. · Боковое ребро – отрезок, соединяющий соответствующие друг другу вершины разных оснований (AA1, BB1, CC1 и DD1). Является общей стороной двух боковых граней. · Высота (h) – это перпендикуляр, проведенный от одного основания к другому, т.е. расстояние между ними. Если боковые ребра расположены под прямым углом к основаниям фигуры, значит они одновременно являются и высотами призмы. · Диагональ основания – отрезок, который соединяет две противолежащие вершины одного и того же основания (AC, BD, A1C1 и B1D1). У треугольной призмы данного элемента нет. · Диагональ боковой грани – отрезок, который соединяет две противолежащие вершины одной и той же грани. На рисунке изображены диагонали только одной грани (CD1 и C1D), чтобы не перегружать его. · Диагональ призмы – отрезок, соединяющий две вершины разных оснований, не принадлежащих одной боковой грани. Мы показали только две из четырех: AC1 и B1D. · Поверхность призмы – суммарная поверхность двух ее оснований и боковых граней. Формулы для расчета площади поверхности (для правильной фигуры) и объема призмы представлены в отдельных публикациях. Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:
Примечание: свойства призмы представлены в отдельной публикации. Варианты сечения призмы 1. Диагональное сечение – секущая плоскость проходит через диагональ основания призмы и два соответствующих боковых ребра.
Примечание: У треугольной призмы нет диагонального сечения, т.к. основанием фигуры является треугольник, у которого нет диагоналей. 2. Перпендикулярное сечение – секущая плоскость пересекает все боковые ребра под прямым углом.
Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем. Виды призм Рассмотрим разновидности фигуры с треугольным основанием. 1. Прямая призма – боковые
грани расположены под прямым углом к основаниям (т.е. перпендикулярны им).
Высота такой фигуры равняется ее боковому ребру. 2. Наклонная призма – боковые
грани фигуры не перпендикулярны ее основаниям. 3. Правильная призма – основаниями являются правильные многоугольники. Может быть прямой или наклонной.
Усеченная
призма –
часть фигуры, оставшаяся после пересечения ее плоскостью, не параллельной
основаниям. Также может быть как прямой, так и наклонной. |
Ссылка 1, 2 Презентация к уроку. |
|
|
Закрепление. Задача 1. В основании прямой четырёхугольной призмы лежит четырёхугольник со сторонами 3см, 6см, 2 см и 4 см. Высота призмы равна 10 см. Найдите площадь боковой поверхности призмы. Решение.
Задача 2. Дана шестиугольная наклонная призма с боковым ребром l=10 см. Периметр сечения призмы плоскостью, перпендикулярной боковому ребру, равен 42 см. Найдите площадь боковой поверхности призмы. Решение.
|
Презентация
|
|
Конец урока |
Рефлексия |
Слайд |
|
|
Домашнее задание: 1. Написать конспект. 2. Выполнить задания 1-3. |
Карточка-задание |
5.Рефлексия по занятию
Рефлексия «+, -, интересно».
- Понравился ли вам урок?
- Что было трудным для вас?
- Что вам больше понравилось?
6. Домашнее задание
Оценочный лист:
|
№ |
Выполненное задание: |
Баллы |
|
1. |
Составить конспект. |
30 |
|
2. |
Выполнить задание 1. |
20 |
|
3. |
Выполнить задание 2. |
20 |
|
4. |
Выполнить задание 3. |
30 |
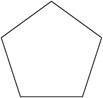
Задание 1.
Найдите для каждой картинки пару
1)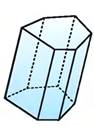 2)
2) 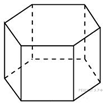 3)
3) 
4)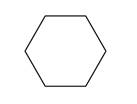 5)
5)
 6)
6)

Задание 2
Какие из перечисленных объектов могут быть элементами призмы? Какими и чем – пояснить.
1) параллельные плоскости
2) отрезок
3) точка
4) четырехугольник
Задание 3.
В правильной четырехугольной призме все ребра равны 2 м. Найти площадь боковой и полной поверхности призмы.
Подпись преподавателя________________________
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.