
|
Название предмета |
Алгебра
|
|
Класс |
9 |
|
УМК (название учебника, автор, год издания) |
Алгебра 9 класс Авт.: Ю.Н.Макарычев |
|
Уровень обучения |
базовый
|
|
Тема урока |
Сумма первых п
членов |
|
Место урока в системе уроков по теме |
2 урок Урок закрепления и применений формулы суммы геометрической прогрессии. |
|
Цель урока |
закрепить понятие суммы геометрической прогрессии; формировать умение применять формулу суммы геометрической прогрессии, совершенствовать навыки решения задач. |
|
Задачи урока
|
Общеобразовательные: расширить и углубить знания о числовых последовательностях, в ввести понятие суммы геометрической прогрессии; вывести формулу суммы геометрической прогрессии, совершенствовать навыки решения задач., показать практическое применение формулы суммы геометрической прогрессии при решении задач. Развивающие: развитие аналитического мышления; познавательной активности мышления, умения работать с текстовой, графической информацией через использование задач моделирующих жизненные ситуации Воспитательные: формирование умения работать в группе.
|
|
Планируемые результаты
|
Учащиеся научатся: Применять формулу суммы геометрической прогрессии; решать задачи с использованием этой формулы. -рассматривать примеры из реальной жизни, иллюстрирующие изменение в геометрической прогрессии - умение аргументировать и обосновывать собственную позицию, уважать разные точки зрения; - умение работать в группах, индивидуально |
|
Техническое обеспечение урока |
мультимедиапроектор, презентация по теме урока |
Сумма первых п членов
геометрической прогрессии
Ход урока
I. Организационный момент.
II. Актуализация знаний обучающихся.
1. Устная работа.
1. Является ли геометрической прогрессией последовательность 5, 20, 80, 320…
2. Назовите два предыдущих и два последующих члена геометрической прогрессии, знаменатель которой равен 3.
…, …, 27 …, … .
3. (bп) – геометрическая прогрессия, q<0.
b2 = -7; b4 = –28, .
b1 – ? b3 – ? q-?
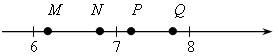
4. Какая из точек, отмеченных на координатной прямой, соответствует числу
![]() .
.
5. Какие из прямых параллельны?
1) у = 4; 2) у = –4х; 3) х = 2х –2; 4) у = 2х.
.
2. Работа у доски по карточкам (2 обучающихся).
Работают вместе с учителем, если возникает необходимость.
Карточка 1.
Найдите сумму первых четырех членов геометрической прогрессии (bп), в которой b1 = 2, b4 =54, q > 0.
Карточка 2.
Найдите сумму пяти первых членов геометрической прогрессии (bп), в которой b2 = 4, b4 = 16, q < 0.
Решение заданий
1. Найдите первый член геометрической прогрессии, в которой S4
= 65, q = ![]() .
.
.
3. Проверочная работа (остальные обучающиеся).
Вариант I Вариант II
Рассматривается геометрическая прогрессия, заданная формулой п-го члена:
bп
= 16 · 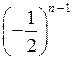 сп
= 27 ·
сп
= 27 · 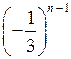
а) Найдите сумму ее первых пяти членов.
б) Сколько надо сложить последовательных членов этой прогрессии, начиная с первого, чтобы получить сумму, равную
![]() ?
?
![]() ?
?
IV. Подведение итогов.
– Сформулировать определение геометрической прогрессии.
– Записать формулу п числа геометрической прогрессии.
– Записать формулу суммы первых членов геометрической прогрессии (q = 1, q ≠ 1).
Домашнее задание.
№ 650а, 652 в, 656
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.