Контрольная работа по дисциплине «Математика»: оформление, написание, методические рекомендации

Яковлева Татьяна Петровна,

доцент кафедры математики и физики

Камчатского государственного университета имени Витуса Беринга,

кандидат педагогических наук, доцент,

г. Петропавловск – Камчатский,

Камчатский край

 

 

 

Контрольная работа по дисциплине «Математика»: оформление, написание, методические  рекомендации

 

 

1. Правила оформления контрольной работы

 

При выполнении контрольной работы по дисциплине «Математика» необходимо строго придерживаться указанных ниже правил:

1.      Контрольная работа выполняется в отдельной тетради в клетку с полями.

2.      На обложке тетради должны быть ясно написаны фамилия, инициалы, название дисциплины, вариант. Титульный лист оформляется в соответствии с требованиями, предъявляемым к контрольным работам.

3.      Номер варианта определяется последней цифрой шифра зачетной книжки. Цифре «0» соответствует вариант 10.

4.      Контрольная работа, содержащая задания не своего варианта, является не зачтенной.

5.      Перед решением каждого задания надо полностью выписать его условие.

6.      Задания располагаются по порядку.

7.      Решения задач следует излагать подробно и аккуратно. При необходимости следует делать соответствующие ссылки с указанием формул, теоретического материала (теоремы, следствия, свойства и др.). Все вычисления, основные и вспомогательные, необходимо делать полностью.

8.      Рисунки и чертежи выполняются карандашом, с помощью линейки.

9.      Контрольная работа должна быть выполнена самостоятельно.

10. Контрольная работа сдается за 10 дней до зачета или экзамена.

2. Контрольные задания

 

В данном пункте даны формулировки контрольных заданий, а необходимые данные для их выполнения берете в пункте 3. из таблиц согласно своего варианта.

 

Задание  1. Множества A и B заданы числовыми промежутками.

Найти:

а)    ;

б)   ;

в)    A \ B;

г)    B \ A;

д)   ;

е)    .

Замечание.  – это дополнение множества A до универсального множества. Универсальным множеством в данном задании является множество действительных чисел.

 

Задание  2. Известно . Найти элементы множеств:

а)    Т;

б)   А;

в)    .

 

Задание  3. Из высказывания С и высказывания L:

а)    образовать конъюнкцию;

б)   образовать дизъюнкцию;

в)    образовать импликацию;

г)    образовать эквиваленцию;

д)    найти значения истинности образованных высказываний.

 

Задание  4. Множество состоит из 7 элементов: a, b, c, d, e, f, g. Если его упорядочивать всеми возможными способами, то во скольких случаях это произойдет при данных (смотри свой вариант) условиях.

 

Задание  5. В закрытой коробке разложено 5 одуванчиков, 6 ромашек, 4 астры, 3 лилии и 2 хризантемы. Найти вероятность того, что взятый наугад цветок будет … (смотри свой вариант).

 

Задание 6. В результате 10 опытов получена выборка. Составить таблицу, которая для нее будет законом распределения.

 

Задание 7. Игральный кубик бросают два раза. Найти вероятность того, что на верхней грани два раза выпадает указанное количество очков.

 

Задание   8.     Дана выборка. Найти:

а)     вариационный ряд;

б)    объем выборки;

в)     моду выборки;

г)     медиану выборки;

д)    среднее выборочное вариационного ряда.

 

 

 

 

3. Задания к вариантам контрольной работы

 

 

Задание 1

 

 

Задание 2

 

 

Задание 3

 

 

Задание 4

 

 

 

Задание 5

 

 

 

Задание 6

 

 

 

Задание 7

 

 

 

Задание 8

 

 

 

 

4. Образец составления варианта

 

 

Оформим текст контрольных заданий на примере варианта 0:

 

Вариант 0

 

Задание  1.  Множества A и B заданы числовыми промежутками А = (–1,1; ∞); .

Найти:

а)     ;

б)    ;

в)     A \ B;

г)     B \ A;

д)    ;

е)     .

 

Задание  2. Известно =. Найти элементы множеств:

а)     Т;

б)    А;

в)     .

 

Задание  3. Из высказывания C – «11 простое число» и высказывания L  –  «6 нечетное число»:

а)     образовать конъюнкцию;

б)    образовать дизъюнкцию;

в)     образовать импликацию;

г)     образовать эквиваленцию;

д)    найти значения истинности образованных высказываний.

 

Задание  4. Множество состоит из 9 элементов: a, b, c, d, e, f, g, t, k. Если его упорядочивать всеми возможными способами, то во скольких случаях элементы a, d, k будут стоять соответственно на 3, 4, 7 местах.

 

Задание  5. В закрытой коробке разложено 5 одуванчиков,  6 ромашек, 4 астры, 3 лилии, 2 хризантемы и 1 тюльпан. Найти вероятность того, что взятый наугад цветок будет ромашка или тюльпан.

 

Задание 6. В результате 10 опытов получена выборка:  2; 5; 2; 3; 4; 3; 4; 3; 5; 2. Составить таблицу, которая для нее будет законом распределения.

 

Задание 7. Игральный кубик бросают два раза. Найти вероятность того, что на верхней грани два раза выпадает четное число очков, не большее 4.

 

Задание   8.     Дана выборка: 1, 0, 2, 1, 3, 0, 2, 0, 9. Найти:

а)     вариационный ряд;

б)    объем выборки;

в)     моду выборки;

г)     медиану выборки;

д)    среднее выборочное вариационного ряда.

 

 

5. Методические рекомендации по выполнению заданий, их решение и оформление

 

 

Задание 1. Множества A и B заданы числовыми промежутками: А = (–1,1; ∞); . Найти:

а)     ;

б)    ;

в)     A \ B;

г)     B \ A;

д)    ;

е)     .

Решение. Изобразим результат операций над множествами A и B сначала на числовой прямой, а затем запишем его в виде числового промежутка, либо пустым множеством, либо объединением двух числовых промежутков (это будет зависеть от того, какие множества A и B). Чтобы получить объединение множеств A и B (), нужно взять все элементы одного множества и присоединить недостающие элементы другого множества. Далее также применить определения , , , ,.

В этой задаче универсальным множеством является множество действительных чисел U = R = (–; +). Тогда , . На числовой прямой изобразим данные множества А и В (рис. 1).

 

Рис. 1.

 

На рисунке 2 изображены множества , , , , .

Разность множеств В и А () – есть пустое множество. По определению:  есть множество, состоящее из всех элементов множества В, которых нет во множестве А. Во множестве В таких элементов нет, так  как .

 

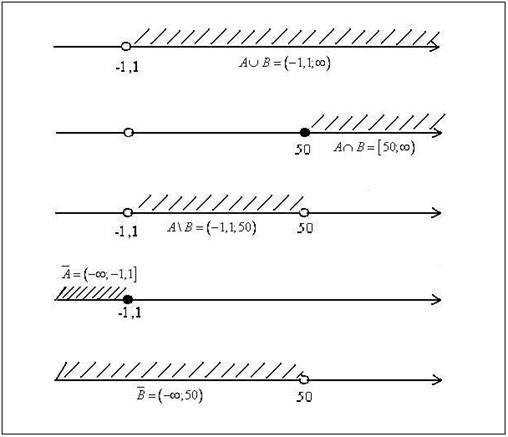
Рис. 2.

 

Ответ:

а)     ;

б)    ;

в)     ;

г);

д)    ;

е)     .

 

Задание 2. Известно =. Найти:

а)     T,

б)    A,

в)     .

Решение.  – есть прямое (декартово) произведение множеств T и A, состоящее из пар, первый элемент которых берется из множества T, второй – из множества A. Значит, T=, A=,                                                  =.

Ответ:

а)     T=,

б)    A=,

в)     =.

 

Задание 3. Из высказывания C – «11 простое число» и высказывания L – «6 нечетное число»:

а)     образовать конъюнкцию;

б)    образовать дизъюнкцию;

в)     образовать импликацию;

г)     образовать эквиваленцию;

д)    найти значения истинности образованных высказываний.

Решение.

а)      Конъюнкцией этих высказываний (CL) является предложение «11 простое число и 6 нечетное число».

б)     Дизъюнкцией этих высказываний (CL) является предложение «11 простое число или 6 нечетное число».

в)     Импликацией этих высказываний (CL) является предложение «Если 11 простое число, то 6 нечетное число».

г)      Эквиваленцией этих высказываний (CL) является предложение «11 простое число тогда и только тогда, когда 6 нечетное число».

д)     Значения истинности всех высказываний внесем в таблицу 1. Для ее заполнения начинаем: с определения значений истинности данных высказываний C и L; затем используем таблицы значений истинности для дизъюнкции, конъюнкции, импликации и эквиваленции. Заметим, если высказывание истинно (верное) ставим 1, если ложно (неверно), то ставим 0 .

 

  Таблица 1

 

 

Задание 4. Множество состоит из 9 элементов: a, b, c, d, e, f, g, t, k. Если множество упорядочивать всеми возможными способами, то во скольких случаях элементы a, d, k будут стоять соответственно на 3, 4, 7 местах.

Решение. Точками представим места, которые должны занимать элементы множества и согласно условия будут всегда занимать элементы a, d, k (рис. 2).

 

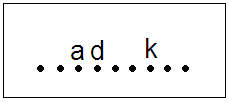
Рис. 2.

 

Оставшиеся 6 букв располагаем на свободных местах. Значит, количество способов их расположения определится числом перестановок, которые можно составить из 6 элементов по формуле: . У нас , следовательно,

.

Ответ: 720.

 

Задание 5. В закрытой коробке разложено 5 одуванчиков, 6 ромашек, 4 астры, 3 лилии и 2 хризантемы, 1 тюльпан. Найти вероятность того, что взятый наугад цветок будет ромашкой или тюльпаном.

Решение. Всего исходов: , то есть .

1-й способ. Нас интересуют только два исхода – взятый наугад цветок ромашка или взятый наугад цветок тюльпан, их количество , то есть . Вводим событие A. A – «событие, состоящее в том, что взятый наугад цветок будет ромашка или тюльпан».

Воспользуемся формулой для вычисления вероятности нашего события A: P (A) =, где m- количество интересующих нас исходов, n- количество всевозможных исходов. Подставим наши данные в формулу, получим:.

Ответ: .

2-й способ. Вводим события: А – «взятый наугад цветок будет ромашка»; В – «взятый наугад цветок будет тюльпан»; С – «взятый наугад цветок будет ромашка или тюльпан». Вероятность события А: . Вероятность события В: . Вероятность события С определяется по формуле . Подставим в нее наши данные .

Ответ: .

 

Задание 6. В результате 10 опытов получена выборка:  2; 2; 2; 3; 3; 3; 4; 4; 5; 5. Составить таблицу, которая для нее будет законом распределения.

Решение. Составим для нашей выборки таблицу, которая является законом распределения вероятностей случайной величины Х (принимающей значения x_i , i = 1; 2; 3; 4). ,  так как , она у нас встречается в выборке 3 раза из 10. Аналогично, ; ; . Проверяем, что . Действительно . Составляем             таблицу 2 – закон распределения.

 

Таблица 2

 

 

Ответ: таблица 2.

 

Задание 7. Игральный кубик бросает два раза. Найти вероятность того, что на верхней грани два раза выпадает четное число очков, не большее 4.

Решение. Вводим события:

Событие A – «событие, состоящее в том, что при подбрасывании кубика первый раз на верхней грани выпадает четное число очков, не большее 4».

Событие B – «событие, состоящее в том, что при подбрасывании кубика второй раз выпадает на верхней грани четное число очков, не большее 4».

Событие C – «событие, состоящее в том, что при подбрасывании кубика на верхней грани оба раза выпадает четное число очков, не большее 4». Тогда событие С вычисляется по формуле .

Интересующие нас исходы события A (то же и для B) – это выпадение 2-х очков и 4-х очков, то есть два исхода. Всего   исходов 6, тогда вероятности событий А, В, С определяются так:

 P (A) ==,   P (B) ==, .

Ответ: .

 

Задание 8. Дана выборка 1, 0, 2, 1, 3, 0, 2, 0, 9. Найти:

а)    вариационный ряд;

б)   объем выборки;

в)    моду выборки;

г)    медиану выборки;

д)   среднее выборочное вариационного ряда.

Решение.

а)     Расположим варианты в порядке возрастания: 0, 0, 0, 1, 1, 2, 2, 3, 9 – это вариационный ряд.

б)    Количество элементов в выборке 9, значит  объем .

в)     Чаще всех в выборке встречается число 0, значит, мода равна 0.

г)     Для нахождения медианы при нечетном количестве вариант берем число, находящееся в середине вариационного ряда, то есть 1.

д)    Среднее выборочное  находим:

.

Ответ: а) 0, 0, 0, 1, 1, 2, 2, 3, 9;   б) 9;   в) 0;  г) 1;  д) 2.