Министерство образования и молодежной политики Свердловской области

ГАПОУ СО «Каменск-Уральский радиотехнический техникум»

 

 

ОДОБРЕНО

цикловой комиссией общеобразовательных дисциплин 

Протокол заседания ЦК № ___  от «__»__________2019 г.

Председатель ЦК ________ (Аркушина А. Н.)

 

 

 

 

 

 

 

 

 

 

 

 

 

КОНТРОЛЬНЫЕ РАБОТЫ

по дисциплине ЕН.01 «Математика»

 

                      по специальности:               

09.02.05 Прикладная информатика

 

 

                                            

 

 

 

 

 

 

 

 

 

 

Каменск-Уральский, 2019 г.

 

Введение

 

Рабочей программой учебной дисциплины ЕН.01 Математика по специальности 09.02.05 Прикладная информатика предусмотрено проведение четырех контрольных работ:

-            контрольная работа № 1 по теме «Основы линейной алгебры»,

-            контрольная работа № 2 по теме «Последовательности и функции», - контрольная работа № 3 по теме «Приложение производной», - контрольная работа № 4 по теме «Интеграл и его приложения».

        

Для каждой контрольной работы приведена система оценивания и перевод полученных баллов в оценку.

 

2

 

Контрольная работа № 1 по теме «Основы линейной алгебры»

 

Критерии оценивания: 

За первое задание студент получает 1 балл (по половине балла за каждый определитель второго порядка), за второе задание – 2 балла, за третье задание – 4 балла (по два балла за каждую систему), за четвертое задание – 7 баллов (за составление расширенной матрицы системы, за осуществление всех трех этапов прямого хода Гаусса, за переход от матрицы к системе уравнений, за вычисление переменных в обратном ходе Гаусса), за пятое задание – 9 баллов (по два балла за вычисление каждого из четырех определителей третьего порядка, за вычисление неизвестных по формулам Крамера). Максимальный балл за работу – 23 балла.

Шкала перевода баллов в оценку:

21 – 23 балла	-      «5» - отлично
17 – 20 баллов	-      «4» - хорошо
12 – 16 баллов	-      «3» - удовлетворительно
0 -  11 баллов	-       «2» - неудовлетворительно

 

Контрольная работа представлена в 28 вариантах.

 

Вариант № 1 1 Вычислить определитель второго порядка:

                         а)       б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)            б)  

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса: 

 

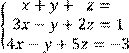
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера:

 

 

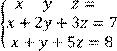
Вариант № 2 1 Вычислить определитель второго порядка:

                        а)       б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)            б)  

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса: 

 

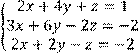
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера:

 

 

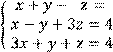
Вариант № 3 1 Вычислить определитель второго порядка:

а)         б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)            б)  

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса: 

 

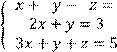
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера:

 

 

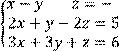
Вариант № 4 1 Вычислить определитель второго порядка:

а)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)            б)  

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса: 

 

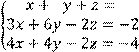
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера:

 

 

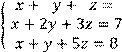
Вариант № 5 1 Вычислить определитель второго порядка:

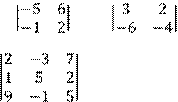
Крамера:

а)                          

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

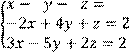
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

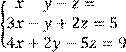
Вариант № 6 1 Вычислить определитель второго порядка:

а)         б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                б) 

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

       

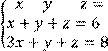
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

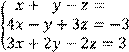
Вариант № 7 1 Вычислить определитель второго порядка:

а)         б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                    б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

 

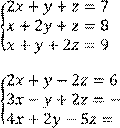
Вариант № 8 1 Вычислить определитель второго порядка:

а)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                    б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

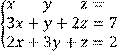
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

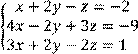
Вариант № 9 1 Вычислить определитель второго порядка:

а)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                 б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

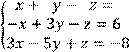
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

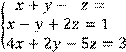
Вариант № 10 1 Вычислить определитель второго порядка:

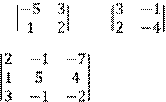
Крамера:

а)                          

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

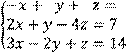
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

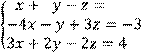
Вариант № 11 1 Вычислить определитель второго порядка:

а)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                    б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

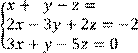
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

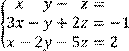
Вариант № 12 1 Вычислить определитель второго порядка:

а)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                      б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

 

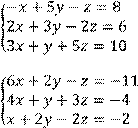
Вариант № 13 1 Вычислить определитель второго порядка:

а)         б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                    б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

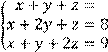
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

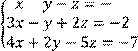
Вариант № 14 1 Вычислить определитель второго порядка:

а)         б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                       б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

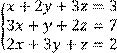
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

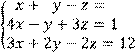
Вариант № 15 1 Вычислить определитель второго порядка:

 

Крамера:

а)                          

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

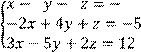
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

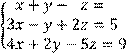
Вариант № 16 1 Вычислить определитель второго порядка:

а)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                         б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

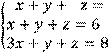
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

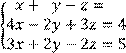
Вариант № 17 1 Вычислить определитель второго порядка:

а)         б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                 б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

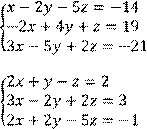
Вариант № 18 1 Вычислить определитель второго порядка:

а)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                        б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

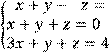
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

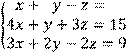
Вариант № 19 1 Вычислить определитель второго порядка:

а)         б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                    б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

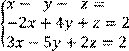
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

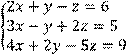
Вариант № 20 1 Вычислить определитель второго порядка:

2 Вычислить определитель третьего порядка:

 

Крамера:

а)                б) 

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

       

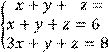
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

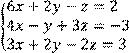
Вариант № 21 1 Вычислить определитель второго порядка:

а)         б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                    б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

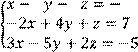
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

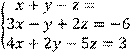
Вариант № 22 1 Вычислить определитель второго порядка:

а)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                б) 

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

 

 

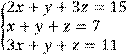
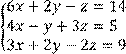
Вариант № 23 1 Вычислить определитель второго порядка:

а)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                    б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

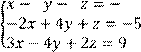
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

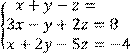
Вариант № 24 1 Вычислить определитель второго порядка:

а)         б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                         б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

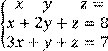
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

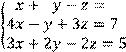
Вариант № 25 1 Вычислить определитель второго порядка:

2 Вычислить определитель третьего порядка:

 

Крамера:

а)                    б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

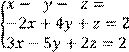
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

 

 

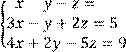
Вариант № 26 1 Вычислить определитель второго порядка:

а)         б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                б) 

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

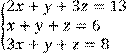
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

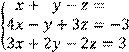
Вариант № 27 1 Вычислить определитель второго порядка:

а)         б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                     б)   

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

 

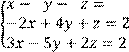
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

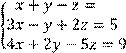
Вариант № 28 1 Вычислить определитель второго порядка:

а)         б)  

2  Вычислить определитель третьего порядка:

 

3  Решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера:

а)                 б) 

4  Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса

       

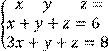
5  Решить систему трех линейных уравнений с тремя неизвестными по формулам Крамера

 

 

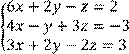
Контрольная работа № 2 по теме «Последовательности и функции»

 

Критерии оценивания: 

За первое – пятое задание студент получает по одному баллу, за шестое - девятое задание – по два балла, за десятое – тринадцатое задание – по три балла. Максимальный балл за работу – 25 баллов.

Шкала перевода баллов в оценку:

23 – 25 баллов	-      «5» - отлично
18 – 22 баллов	-      «4» - хорошо
13 – 17 баллов	-      «3» - удовлетворительно
0 -  12 баллов	-       «2» - неудовлетворительно

 

Контрольная работа представлена в 6 вариантах.

 

Вариант 1 Найдите предел функции:

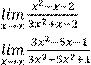
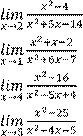
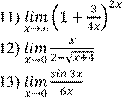
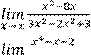
1)     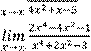                                                                                              6)                 

2)                                                                                                   7)

 

3)                                                                                                   8)

4)                                                                                                   9)

5)                                                                           

Найдите предел функции:

Вариант 2

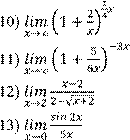
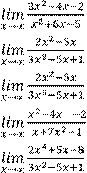
1)   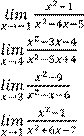                                                                                                6) 

2)                                                                                                   7)

 

3)                                                                                                   8)

4)                                                                                                   9)

5)

Найдите предел функции:

Вариант 3

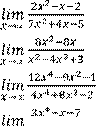
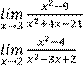
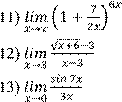
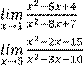
1)     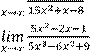                                                                                              6)                

2)                                                                                                   7)

 

3)                                                                                                   8)

4)                                                                                                   9) 

5)                                                  

 

Вариант 4 Найдите предел функции:

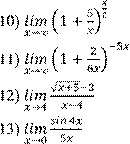
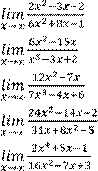
1)   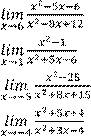                                                                                                6)

2)                                                                                                   7) 

3)                                                                                                   8) 

4)                                                                                                   9)

5)  

Найдите предел функции:

Вариант 5

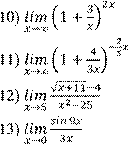
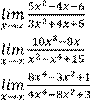
1)   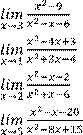                                                                                                6)

2)                                                                                                   7)

 

3)                                                                                                   8)

4)                                                                                                          9)          

5)                                                                                                             

Найдите предел функции:

Вариант 6

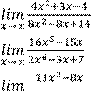
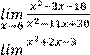
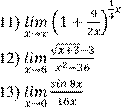
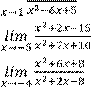
1)     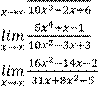                                                                                              6)            

2)                                                                                                   7)

 

3)                                                                                                   8) 

4)                                                                                                   9)

5) 

 

Контрольная работа № 3 по теме «Приложение производной»

 

Критерии оценивания: 

Студент получает по одному баллу за нахождение области определения функции, за определение точек пересечения с осями координат, за нахождение производной функции, за нахождение критических точек, за определение промежутков возрастания (убывания) функции и точек максимума и минимума, за нахождение значения функции в точках минимума и максимума, за нахождение второй производной, за определение критической точки, за определение промежутков выпуклости (вогнутости) и точек перегиба, за определение значения функции в точках перегиба, за построение графика функции, за выделение критических точек принадлежащих заданному интервалу, за нахождение значения функции в концах интервала, за определение наибольшего и наименьшего значения функции на заданном интервале. Максимальный балл за работу – 14 баллов.

Шкала перевода баллов в оценку:

14 баллов	-      «5» - отлично
11 – 13 баллов	-      «4» - хорошо
7 – 10 баллов	-      «3» - удовлетворительно
0 -  6 баллов	-       «2» - неудовлетворительно

 

Контрольная работа представлена в 12 вариантах.

 

Вариант 1

Исследовать функцию  и построить ее график. Найти наибольшее и наименьшее значение функции на интервале [-2;1].

 

Вариант 2

Исследовать функцию  и построить ее график. Найти наибольшее и наименьшее значение функции на интервале [0;3].

 

Вариант 3

Исследовать функцию  и построить ее график. Найти наибольшее и наименьшее значение функции на интервале [2;5].

 

Вариант 4

Исследовать функцию  и построить ее график. Найти наибольшее и наименьшее значение функции на интервале [-3;0].

 

Вариант 5

Исследовать функцию  и построить ее график. Найти наибольшее и наименьшее значение функции на интервале [0;3].

 

Вариант 6

Исследовать функцию  и построить ее график. Найти наибольшее и наименьшее значение функции на интервале [0;4].

 

Вариант 7

Исследовать функцию  и построить ее график. Найти наибольшее и наименьшее значение функции на интервале [-2;2].

 

Вариант 8

Исследовать функцию  и построить ее график.   Найти наибольшее и наименьшее значение функции на интервале [-1;1]. Вариант 9

Исследовать функцию  и построить ее график. Найти наибольшее и наименьшее значение функции на интервале [0;5].

 

Вариант 10

Исследовать функцию  и построить ее график. Найти

наибольшее и наименьшее значение функции на интервале [-1;4]

 

Вариант 11

Исследовать функцию   и построить ее график. Найти наибольшее и наименьшее значение функции на интервале [-3;2].

 

Вариант 12

Исследовать функцию  и построить ее график. Найти наибольшее и наименьшее значение функции на интервале [-1;2].

 

Контрольная работа № 4 по теме «Интеграл и его приложения»

 

Критерии оценивания: 

За первое задание студент получает один балл, за второе задание – три балла, за третье задание – два балла, за четвертое и пятое задание по три балла. Максимальный балл за работу – 12 баллов.

Шкала перевода баллов в оценку:

11 – 12 баллов	-      «5» - отлично
9 – 10 баллов	-      «4» - хорошо
6 – 8 баллов	-      «3» - удовлетворительно
0 -  5 баллов	-       «2» - неудовлетворительно

 

Контрольная работа представлена в 4 вариантах.

 

Вариант 1

1  Вычислить интеграл  

2  Вычислить интеграл методом замены переменной:  

3  Вычислить определенный интеграл  

4  Вычислить методом интегрирования по частям интеграл  

5  Найти площадь фигуры, ограниченной линиями: ,  ,  ,   

 

Вариант 2

1  Вычислить интеграл  

2  Вычислить интеграл методом замены переменной:  

3  Вычислить определенный интеграл  

4  Вычислить методом интегрирования по частям интеграл  

5  Найти площадь фигуры, ограниченной линиями: ,  ,  ,   

 

Вариант 3

1  Вычислить интеграл  

2  Вычислить интеграл методом замены переменной:  

3  Вычислить определенный интеграл  

4  Вычислить методом интегрирования по частям интеграл  

5  Найти площадь фигуры, ограниченной линиями: ,  ,  ,   

 

Вариант 4

1  Вычислить интеграл  

2  Вычислить интеграл методом замены переменной:  

3  Вычислить определенный интеграл  

4  Вычислить методом интегрирования по частям интеграл  

5  Найти площадь фигуры, ограниченной линиями: ,  ,  ,