Круги Эйлера

Круги Эйлера

Цели: ознакомить учащихся с возможностями иллюстрации соотношения между множествами с помощью кругов Эйлера; продолжить формировать умения находить объединение и пересечение множеств.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Пусть даны множества А = {х | х – имя девочки} и В = {х | х – имя мальчика}. Выпишите:

а) два элемента, принадлежащих множеству А, но не принадлежащих множеству В;

б) два элемента, принадлежащих множеству В, но не принадлежащих множеству А;

в) два элемента, принадлежащих и множеству А, и множеству В;

г) два элемента, не принадлежащих ни множеству А, ни множеству В.

2. Найдите А В, если:

а) А = {0, 1, 2, 3, 4} и В = {1, 2, 3, 4, 5};

б) А = {х | х – двузначное число} и В = {х | х – число, меньше 75}.

3. Найдите А В, если:

а) А = {17, 18, 19} и В = {3};

б) А = {у | у – число, меньшее 32} и В = {у | у – число, большее 7, но меньшее 45}.

III. Объяснение нового материала.

1. М о т и в а ц и я   и з у ч е н и я.

Предложим учащимся для решения задачу, которую достаточно трудно решить без наглядного представления информации.

З а д а ч а. В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 – в биологическом, 10 ребят не посещают кружки. Сколько биологов увлекаются математикой?

Р е ш е н и е

Изобразим различные множества учащихся в виде кругов. Большой круг будет изображать всех учащихся класса. В этот круг поместим два поменьше. Один обозначим буквой М, и он будет изображать математиков класса. Другой круг обозначим Б – биологи класса. Очевидно, в общей части кругов, обозначенной МБ, окажутся те самые биологи-математики, которые нас интересуют. Теперь посчитаем: всего внутри большого круга 35 ребят, внутри двух меньших 35 – 10 = 25 ребят. Внутри «математического» круга М находятся 20 ребят, значит, в той части «биологического» круга, которая расположена вне круга М, находятся 25 – 20 = 5 биологов, не посещающих математический кружок. Остальные биологи, их 11 – 5 = 6 человек, находятся в общей части кругов МБ. Там образом, 6 биологов увлекаются математикой.

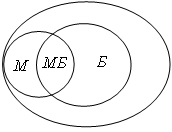
О т в е т: 6 биологов увлекаются математикой.

2. С о о б щ а е м   у ч а щ и м с я,  что эти круги называются кругами Эйлера.

Один из величайших математиков петербургской академии Леонард Эйлер (1707–1783) за свою долгую жизнь написал более 850 научных работ. В одной из них появились круги, которые «очень подходят для того, чтобы облегчить наши размышления». С помощью этих кругов удобно геометрически иллюстрировать операции над множествами. Можно рисовать не только круги, но и овалы, прямоугольники и другие геометрические фигуры.

В учебнике на с. 169–170 рассматриваем иллюстрацию пересечения и объединения двух множеств с помощью кругов Эйлера.

IV. Формирование умений и навыков.

На этом уроке учащиеся решают качественно новые упражнения, в которых необходимо рассматривать множества различной природы, а не только числовые. Востребуются знания из других разделов математики.

1. № 803.

2. Известно, что точки A, B, C и D расположены на одной прямой, причём пересечением множеств точек отрезков AB и CD являются:

а) отрезок CD;         б) отрезок СВ.

Для каждого случая сделайте чертёж.

Р е ш е н и е

а) 

б) 

3. № 804 (а).

Р е ш е н и е

– Вспомним определения.

Прямоугольником называется параллелограмм, у которого есть прямой угол.

Ромбом  называется  параллелограмм,  у  которого  смежные  стороны равны.

Изобразим соотношение множества этих фигур с помощью кругов Эйлера.

Пересечением двух множеств будет множество параллелограммов, у которых есть прямой угол и равны смежные стороны. Это множество квадратов.

О т в е т: множество квадратов.

4. № 805.

Р е ш е н и е

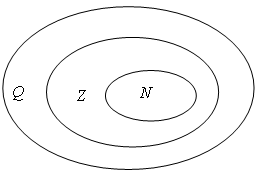
Из темы «Действительные числа» учащиеcя знают, что N Z Q R.

а) N Z = N;   N Z = Z;

б) Z Q = Z;   Z Q = Q;

в) Q I = ;   Q I = R.

5. № 806.

Р е ш е н и е

А = {х | х – кратное 4},

В = {у | у – кратное 3}.

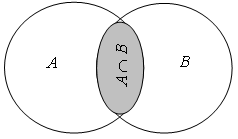
А В – множество чисел, которые одновременно делятся на 3 и на 4, значит, это множество чисел, кратных 12.

О т в е т:  А В = {z | z – кратное 12}.

6. № 808 (а).

Р е ш е н и е

Х У = ;

Х У = N \ {1}.

Так как по определению:

– натуральное число называется простым, если оно имеет только два различных делителя: 1 и само это число;

– число, имеющее более двух делителей, называется составным;

– число 1 не относится ни к простым, ни к составным, так как имеет только один делитель.

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Для чего служат круги Эйлера?

– Как с помощью кругов Эйлера изобразить пересечение множеств? объединение множеств?

Домашнее задание.

1. № 804 (б), № 807, № 808 (б).

2. № 937.