
Лабораторная работа № 3. ГРАФИКИ ФУНКЦИЙ
1 ЦЕЛЬ РАБОТЫ
Изучить основные методы создания графиков в среде MATLAB.
2 КРАТКИЕ СВЕДЕНИЯ
MATLAB предоставляет обширные возможности для визуализации функций одной и двух переменных. Использование функций для построения графиков с минимальным набором задаваемых параметров (остальные выбираются автоматически) приводит к получению качественных графиков. MATLAB позволяет строить графики функций в линейном, логарифмическом и полулогарифмическом масштабах. Причем в одном окне можно строить графики нескольких функций, даже определенных на разных отрезках.
3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
ПРИМЕР 1 Графики в линейном масштабе
Построение графиков функций одной переменной в линейном масштабе осуществляется при помощи функции plot. В зависимости от входных аргументов функция plot позволяет строить один или несколько графиков, изменять цвет и стиль линий и добавлять маркеры на каждый график. Приведем простейший пример (рис. 4):
>> x = 0:0.005:1;
>> y = exp(-x).*sin(10*x);
>> plot(x, y)
>>
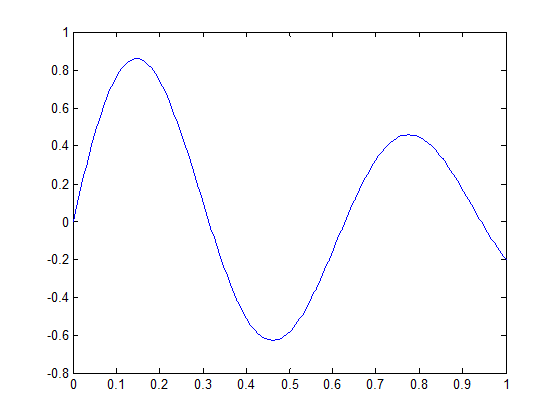
Рис. 4. График одной функции
Сравнение нескольких функций легко
производить, построив графики на одних
координатных осях. Постройте графики функций ![]() и
и ![]() на отрезке
на отрезке ![]() . Сгенерируйте
вектор-строку значений
аргумента х и вектор-строки f и g, содержащие значения функций. Команда plot с двумя парами аргументов приводит к графику, изображенному на рис. 5.
. Сгенерируйте
вектор-строку значений
аргумента х и вектор-строки f и g, содержащие значения функций. Команда plot с двумя парами аргументов приводит к графику, изображенному на рис. 5.
>> x = -2*pi:0.01:2*pi;
>> f = exp(-0.1*x).*sin(x).^2;
>> g = exp(-0.2*x).*sin(x).^2;
>> plot(x, f, x, g)
>>
Аналогичным образом при помощи задания в plot через запятую пар аргументов: вектор абсцисс, вектор ординат, осуществляется построение графиков произвольного числа функций.
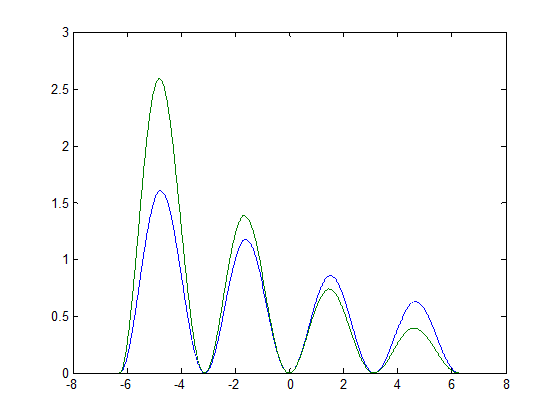
Рис. 5. Графики двух функций
Для построения графиков в логарифмическом и полулогарифмическом масштабах служат функции:
- loglog (логарифмический масштаб по обеим осям);
- semilogx (логарифмический масштаб только по оси абсцисс);
- semilogy (логарифмический масштаб только по оси ординат).
Аргументы loglog, semilogx и semilogy задаются в виде пары векторов значений абсцисс и ординат так же, как для функции plot.
Постройте графики функций ![]() и
и ![]() на отрезке
[0.1, 5] в логарифмическом масштабе по оси х:
на отрезке
[0.1, 5] в логарифмическом масштабе по оси х:
>> x = 0.1:0.01:10;
>> f = log(0.5*x);
>> g = sin(log(x));
>> semilogx(x, f, x, g)
>>
Получающиеся графики изображены на рис. 6.
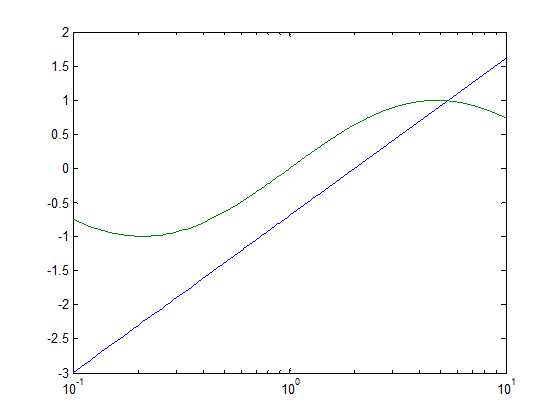
Рис. 6. Графики в полулогарифмической шкале
ПРИМЕР 2 Изменение свойств линий и оформление графиков
Построенные в первом примере графики функций должны быть максимально удобными для восприятия. Часто требуется нанести маркеры, изменить цвет линий, а при подготовке к монохромной печати – задать тип линии (сплошная, пунктирная, штрих-пунктирная и т. д.). MATLAB предоставляет возможность управлять видом графиков, построенных при помощи plot, loglog, semilogx и semilogy, для чего служит дополнительный аргумент, помещаемый за каждой парой векторов. Этот аргумент заключается в апострофы и состоит из трех символов, которые определяют: цвет, тип маркера и тип линии. Используются одна, две или три позиции, в зависимости от требуемых изменений. В табл. 1 приведены возможные значения данного аргумента с указанием результата.
Например, для построения первого графика на рис. 5 красными точечными маркерами без линии, а второго – пунктирной черной линией следует использовать команду plot(x, f, ‘r.’, x, g, ‘k:’). При этом абсциссы маркеров будут совпадать со значениями аргумента, содержащимися в х. Это не всегда хорошо, ведь для получения гладкой кривой требуется вычислить вектор значений функции в достаточно большом числе точек, что приводит к слишком частому расположению маркеров или даже их перекрытию. Простой прием позволяет поместить маркеры в заранее выбранные позиции. Строится два графика функции, один – сплошной линией, а второй – только маркерами для небольшого набора значений аргумента (рис. 7):
>> x = -1:0.01:1;
>> y = sin(2*pi*x.^2);
>> xm = -1:0.2:1;
>> ym = sin(2*pi*xm.^2);
>> plot(x, y, 'k', xm, ym, 'ko');
>>
Таблица 1
|
Цвет |
Тип маркера |
Тип линии |
|||
|
y |
желтый |
. |
точка |
- |
сплошная |
|
m |
розовый |
o |
кружок |
: |
пунктирная |
|
c |
голубой |
x |
крестик |
-. |
штрих-пунктирная |
|
r |
красный |
+ |
знак «плюс» |
-- |
штриховая |
|
g |
зеленый |
* |
звездочка |
|
|
|
b |
синий |
s |
квадрат |
|
|
|
w |
белый |
d |
ромб |
|
|
|
k |
черный |
v |
треугольник вершиной вниз |
|
|
|
|
|
^ |
треугольник вершиной вверх |
|
|
|
|
|
< |
треугольник вершиной вправо |
|
|
|
|
|
> |
треугольник вершиной влево |
|
|
|
|
|
p |
пятиконечная звезда |
|
|
|
|
|
h |
шестиконечная звезда |
|
|
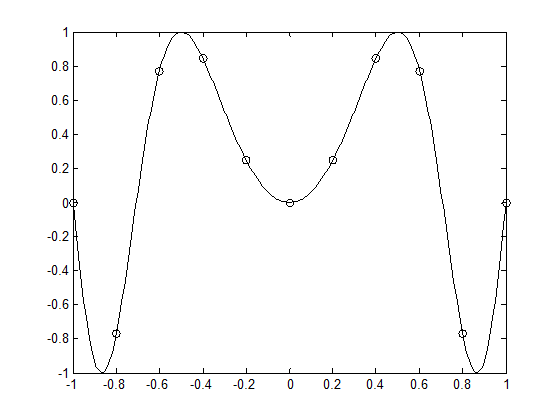
Рис. 7. График функции с использованием маркеров
Удобство использования графиков во многом зависит от дополнительных элементов оформления: координатной сетки, подписей к осям, заголовка и легенды. Такие возможности реализуются либо с помощью дополнительных параметров, задающих свойства объектов, либо с помощью вспомогательных команд и функций. Перечислим основные из них. Сетка наносится командой grid on, функции xlabel, ylabel служат для размещения подписей к осям, а title – для заголовка. При необходимости сопроводить график легендой следует использовать функцию legend. Все перечисленные команды применимы к графикам как в линейном, так и в логарифмическом и полулогарифмическом масштабах. Следующие команды выводят графики изменения суточной температуры, изображенные на рис. 8, которые снабжены всей необходимой информацией.
>> time = [0 4 7 9 10 11 12 13 13.5 14 14.5 15 16 17 18 20 22];
>> temp1 = [14 15 14 16 18 17 20 22 24 28 25 20 16 13 13 14 13];
>> temp2 = [12 13 13 14 16 18 20 20 23 25 25 20 16 12 12 11 10];
>> plot(time, temp1, 'ro-', time, temp2, 'go-')
>> grid on
>> title('Суточные температуры')
>> xlabel('Время (час.)')
>> ylabel('Температура(С)')
>> legend('10 мая','11 мая')
>>
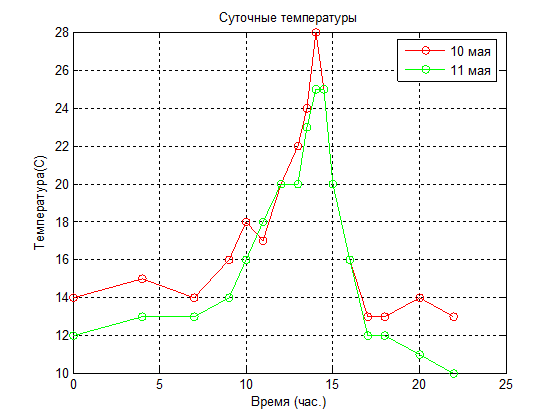
Рис. 8. Пример оформления графика
4 КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Для чего применяется функция plot?
2. Какие функции служат для построения графиков в логарифмическом и полулогарифмическом масштабах?
3. Каким образом MATLAB предоставляет возможность управлять видом графиков?
4. С помощью какой команды включается отображение сетки на графике?
5. Для чего служат функции xlabel, ylabel, tittle и legend?
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.