
Федеральное агентство по образованию
Федеральное государственное образовательное учреждение высшего профессионального образования
«Сибирский федеральный университет»
ГЕОИНФОРМАЦИОННЫЕ СИСТЕМЫ
И ТЕХНОЛОГИИ
Направление 120100 – “Геодезия и дистанционное зондирование”
Специальность 120201 «Исследование природных ресурсов аэрокосмическими методами»
Красноярск – 2007
Содержание
ТЕМА 1. ГЕОИНФОРМАТИКА И ГЕОИНФОРМАЦИОННЫЕ СИСТЕМЫ..............................4
ТЕМА 2. МОДЕЛЬ ДАННЫХ ВЕКТОРНЫХ ГИС................................................................................10
УРОВНИ ЛОКАЛИЗАЦИИ ОБЪЕКТОВ В ВЕКТОРНЫХ ГИС .........................................................................11
Точечные данные..............................................................................................................................11
Линейные данные .............................................................................................................................11
Площадные данные..........................................................................................................................12
МОДЕЛЬ ДАННЫХ ВЕКТОРНЫХ ГИС .......................................................................................................14
РАБОТА С ТОПОЛОГИЧЕСКОЙ ИНФОРМАЦИЕЙ В ВЕКТОРНЫХ ГИС.........................................................16
ТЕМА 3. ПРОСТРАНСТВЕННЫЕ ОТНОШЕНИЯ В ГИС-АНАЛИЗЕ.........................................18
ТОПОЛОГИЧЕСКАЯ СТРУКТУРА ЦИФРОВОЙ КАРТЫ.................................................................................18
АЛГОРИТМЫ ВЫЧИСЛИТЕЛЬНОЙ ГЕОМЕТРИИ.........................................................................................20
Пересечение линий............................................................................................................................20
Операции с полигонами....................................................................................................................23
Точка внутри или снаружи полигона .............................................................................................24
Определение особых точек полигона .............................................................................................25
ОВЕРЛЕЙ ПОЛИГОНОВ .............................................................................................................................26
ТЕМА 4. ВВОД ПРОСТРАНСТВЕННЫХ ДАННЫХ В ГИС...........................................................31
ПЕРИФЕРИЙНЫЕ УСТРОЙСТВА ЭВМ ДЛЯ ВВОДА ДАННЫХ В ГИС..........................................................32
ОЦИФРОВКА КАРТЫ................................................................................................................................35 СВОДКА СЕГМЕНТОВ ГИС-ПРОЕКТА.......................................................................................................36
ГЕНЕРАЛИЗАЦИЯ КАРТОГРАФИЧЕСКОГО ИЗОБРАЖЕНИЯ В ГИС.............................................................37
ТЕМА 5. ПРИВЯЗКА ГЕОДАННЫХ К КАРТЕ И ПРЕОБРАЗОВАНИЯ КООРДИНАТ.....................41
МАТЕМАТИЧЕСКАЯ ОСНОВА И ПРОЕКЦИИ ЦИФРОВЫХ КАРТ..................................................................41
КАРТОГРАФИЧЕСКАЯ ПРОЕКЦИЯ ГАУССА...............................................................................................41
Формулы проекции Гаусса...............................................................................................................42
Система координат Гаусса-Крюгера............................................................................................44
ПРЕОБРАЗОВАНИЯ СИСТЕМ КООРДИНАТ КАРТОГРАФИЧЕСКИХ ПРОЕКЦИЙ ............................................44
ТЕМА 6. ВЕКТОРИЗАЦИЯ КАРТОГРАФИЧЕСКОГО ИЗОБРАЖЕНИЯ ..................................50
ПРЕДОБРАБОТКА ОТСКАНИРОВАННОЙ КАРТЫ ........................................................................................51
РАЗБИЕНИЕ КАРТЫ НА ТЕМАТИЧЕСКИЕ СЛОИ ........................................................................................51
ВЫДЕЛЕНИЕ ГРАНИЦ. ГРАДИЕНТНЫЕ ФИЛЬТРЫ......................................................................................52
ОПЕРАТОРЫ МАТЕМАТИЧЕСКОЙ МОРФОЛОГИИ......................................................................................53
АЛГОРИТМЫ РАСТРОВО-ВЕКТОРНОГО ПРЕОБРАЗОВАНИЯ.......................................................................56
СЕГМЕНТАЦИЯ ЧЕРЕЗ ПОДБОР МОДЕЛИ. ПРЕОБРАЗОВАНИЕ ХОХА.........................................................58
ТЕМА 7. ГЛОБАЛЬНЫЕ СИСТЕМЫ ПОЗИЦИОНИРОВАНИЯ..................................................62
ПРИНЦИПЫ РАБОТЫ GPS.........................................................................................................................63
Определение местоположения по расстояниям до спутников...................................................63
Измерение расстояния до спутника ..............................................................................................64
Обеспечение совершенной временной привязки.............................................................................65
Определение положения спутника в космосе................................................................................66
Ионосферные и атмосферные задержки сигналов.......................................................................67
Другие виды погрешностей.............................................................................................................68
ОБЗОР ПОРТАТИВНЫХ GPS-ПРИЕМНИКОВ..............................................................................................69
ТЕМА 8. РАСТРОВЫЕ ГИС: МОДЕЛЬ ДАННЫХ И АЛГОРИТМЫ АНАЛИЗА.....................71
ПРОСТРАНСТВЕННЫЙ АНАЛИЗ В РАСТРОВЫХ ГИС.................................................................................74
Описание характеристик растра..................................................................................................74
Локальные операции ........................................................................................................................74
Фокальные операции........................................................................................................................76
Зональные операции.........................................................................................................................77 ТЕМА 9. ФИЗИЧЕСКАЯ ОРГАНИЗАЦИЯ ПРОСТРАНСТВЕННЫХ ДАННЫХ ГИС............78
ХРАНЕНИЕ РАСТРОВЫХ ДАННЫХ ............................................................................................................78
ИЕРАРХИЧЕСКИЕ СТРУКТУРЫ ДАННЫХ...................................................................................................80
АЛГОРИТМЫ НА КВАДРОДЕРЕВЬЯХ .........................................................................................................83
ПРОСТРАНСТВЕННЫЕ ИНДЕКСЫ..............................................................................................................84
ТЕМА 10. МОДЕЛИ 3D – ПОВЕРХНОСТЕЙ В ГИС ........................................................................86
РАСТРОВЫЕ ЦИФРОВЫЕ МОДЕЛИ МЕСТНОСТИ........................................................................................87
НЕРЕГУЛЯРНЫЕ ТРИАНГУЛЯЦИОННЫЕ СЕТИ (TIN) ................................................................................92
ТЕМА 11. ГЕОДЕЗИЯ И ЦИФРОВАЯ ФОТОГРАММЕТРИЯ В ГИС ..........................................98
ОПРЕДЕЛЕНИЕ ПРЯМОУГОЛЬНЫХ КООРДИНАТ ТОЧЕК ............................................................................98
Полярная засечка............................................................................................................................100
Прямая угловая засечка................................................................................................................102
Линейная засечка............................................................................................................................103
Триангуляция, трилатерация и полигонометрия........................................................................104
ЦИФРОВАЯ ФОТОГРАММЕТРИЯ .............................................................................................................105 Получение изображения................................................................................................................106
Системы координат......................................................................................................................107
Внутреннее ориентирование снимка ...........................................................................................108
Внешнее ориентирование снимка.................................................................................................109
Последовательность операций при фотограмметрической обработке......................................111
ТЕМА 12. КАРТОГРАФИЧЕСКИЕ МОДЕЛИ СТРУКТУРЫ ЯВЛЕНИЙ В ГИС ....................113
МОДЕЛИ АППРОКСИМАЦИИ ПОВЕРХНОСТЕЙ ГЕОГРАФИЧЕСКИХ РАСПРЕДЕЛЕНИЙ..............................113
МОДЕЛИ ПРОСТРАНСТВЕННОГО РАЗМЕЩЕНИЯ ТОЧЕЧНЫХ ОБЪЕКТОВ.................................................116
Карта плотности населения ........................................................................................................116
Модель равномерности размещения населенных пунктов.........................................................117
Карты потенциала поля расселения............................................................................................118
МОДЕЛИРОВАНИЕ ТИПОЛОГИЧЕСКИХ СИНТЕТИЧЕСКИХ ХАРАКТЕРИСТИК ..........................................119
ТЕМА 13. КАРТОГРАФИЧЕСКИЕ МОДЕЛИ ВЗАИМОСВЯЗИ ЯВЛЕНИЙ В ГИС...............124
КОЭФФИЦИЕНТ СООТВЕТСТВИЯ ПЛОЩАДЕЙ, МАТРИЦА СХОДСТВА И 2 - СТАТИСТИКА......................124
ИНФОРМАЦИОННЫЕ МОДЕЛИ ВЗАИМОСВЯЗИ ЯВЛЕНИЙ .......................................................................126
КОРРЕЛЯЦИОННЫЕ МОДЕЛИ ВЗАИМОСВЯЗИ ЯВЛЕНИЙ .........................................................................128
ТЕМА 14. КАРТОГРАФИЧЕСКИЕ МОДЕЛИ ДИНАМИКИ ЯВЛЕНИЙ В ГИС .....................131
МЕТОД МОНТЕ-КАРЛО..........................................................................................................................131
“ГРАВИТАЦИОННЫЕ” МОДЕЛИ ПРОСТРАНСТВЕННОГО РАСПРОСТРАНЕНИЯ ЯВЛЕНИЙ.........................134
ТЕМА 15. ИНСТРУМЕНТАЛЬНЫЕ СРЕДСТВА СОЗДАНИЯ ГИС-ПРИЛОЖЕНИЙ...........136
ТЕМА 16. ВЫВОД ДАННЫХ В ГИС..................................................................................................139
ПЕРИФЕРИЙНЫЕ УСТРОЙСТВА ВЫВОДА ИНФОРМАЦИИ В ГИС.............................................................139
ПОДГОТОВКА КАРТ К ИЗДАНИЮ............................................................................................................140
Рамка карты и зарамочное оформление .....................................................................................141
Размещение подписей географических объектов на карте.......................................................141
ПРЕДСТАВЛЕНИЕ КАРТ И КОСМИЧЕСКИХ СНИМКОВ В ИНТЕРНЕТ.........................................................142 Картографический сервер UMN MapServer................................................................................143
Размещение растровых карт. Сервер MapIT!. ...........................................................................146
ТЕМА 17. ЗАКЛЮЧЕНИЕ: БУДУЩЕЕ ГИС....................................................................................147
ЛИТЕРАТУРА.........................................................................................................................................149
Тема 1. Геоинформатика и геоинформационные системы
В 1990-х годах в нашей стране усилился интерес к геоинформатике – научно-техническому комплексу, объединяющему одноименную отрасль научного знания, технологию и прикладную деятельность, связанные с разработкой и реализацией географических информационных систем (ГИС) .
Геоинформатика охватывает научную, техническую и производственную сферы. Геоинформатика как наука изучает природные и социальноэкономические геосистемы, их структуру, связи, динамику, функционирование в пространстве-времени посредством компьютерного моделирования на основе пространственных баз данных. Геоинформатика как технология изучает законы образования и функционирования пространственно-временной информации, связанной с географическими объектами и явлениями, её свойства, методы сбора, обработки, хранения, анализа и распространения. Геоинформационные технологии в этом случае рассматриваются как метод по отношению к географии, экономике, социологии и т.п. Геоинформатика как производство включает разработку аппаратных и программных средств ГИС, создание баз данных, цифровых карт, приложений.
Геоинформатика как наука имеет междисциплинарный характер, и сформировалась на стыке таких дисциплин, как география, информатика, картография, геодезия, теория информационных систем и баз данных, а также других дисциплин с привлечением общенаучных методов познания, таких как системный подход, моделирование. Этот список в настоящее время расширяется (пространственная статистика, Internet). Геоинформатика наиболее тесно связана с картографическими методами.
Геоинформационные системы являются технологической основой геоинформатики. Из множества встречающихся определений ГИС можно сказать, что информационная система является географической, если в ней интегрируются данные и знания о территории, которые используются для решения научных и прикладных географических задач, связанных с инвентаризацией, пространственным анализом и моделированием, прогнозированием, управлением экономикой, территориальным развитием общества, защитой окружающей среды.
В литературе ГИС чаще всего классифицируются по проблемнотематической ориентации, назначению, территориальному охвату, способу организации географических данных. В зависимости от характера решаемых задач выделяют информационно-справочные, мониторинговые, инвентаризационные, исследовательские, учебные, издательские, поддержки принятия решений. По области применения ГИС можно классифицировать на следующие виды: экологические и природопользовательские, социальноэкономические, земельно-кадастровые, геологические, инженерных коммуникаций и городского хозяйства, чрезвычайных ситуаций, навигационные, транспортные, торгово-маркетинговые, археологические и т.д. По территориальному охвату выделяются глобальные, общенациональные, региональные, локальные, муниципальные ГИС.
Несмотря на все многообразие задач, решаемых на основе геоинформационных технологий, во всех ГИС можно выделить некоторые блоки, выполняющие приблизительно одинаковые функции. К числу таких «обязательных» блоков относятся блоки сбора и ввода данных, обработки, моделирования и анализа, распространения и использования в процессах принятия решений (рисунок 1.1). Исторически ГИС функционально развивались от задач инвентаризации к анализу и моделированию, а затем – к автоматизированному принятию решений.
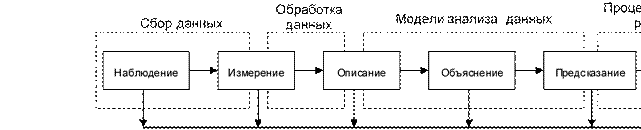
Рисунок 1.1 – Функции геоинформационной системы
Основной особенностью ГИС является географическая привязка обрабатываемых данных. Представление в ЭВМ географических объектов и явлений предполагает формализованное описание их позиционных и непозиционных свойств. Пространственно - распределенная информация в ГИС кодируется в одной из моделей пространственных данных, а атрибутная информация – в виде реляционных таблиц, обрабатываемых СУБД. При выборе цифрового представления географических объектов и явлений обычно учитываются следующие критерии: точность представления, достоверность прогнозов и решений, принятых на основе выбранного представления, объем данных, скорость вычислений, совместимость с программным обеспечением.
В геоинформационных системах используется особое – пространственное представление географических объектов и явлений. Восприятие окружающего мира можно свести к пониманию протекающих в нем явлений, описание которых в какой-либо форме мы называем данными. Географические явления бесконечно сложны и разнообразны. Чем ближе мы находимся к географическому объекту, тем больше деталей мы можем видеть. Поэтому для абсолютно точного описания сущностей реального мира потребовались бы бесконечно большие базы данных. Для того, чтобы быть обработанными в компьютере, данные должны быть редуцированы до конечных размеров.
Данные – зарегистрированные факты о явлениях. Знание – опытно проверенный результат познания действительности, верное её отражение в мышлении человека, обладание опытом и пониманием, которые являются правильными и в субъективном, и в объективном отношении, и на основании которых можно строить суждения и выводы, кажущиеся достаточно надежными для того, чтобы рассматриваться как знание. Если в результате переработки данных возникает приращение знания, то это приращение – информация.
При описании данных на естественном языке сами данные и их интерпретация обычно фиксируются совместно. В компьютерном представлении данные и интерпретация разделены: программы обычно имеют дело с данными как таковыми, а семантика часто вообще не фиксируется в явном виде. Задачу интерпретации данных возлагают на программу, использующую некоторую модель данных.
База данных в ГИС – больше, чем просто хранилище данных; данные в ней организованы особым образом, чтобы обеспечить работу с пространственными географическими данными. Далее понятие базы данных будет рассматриваться как представление или модель сущностей окружающего мира для специфического «пространственного» применения. Создание базы данных может требовать до 75% затрат на реализацию проекта ГИС.
Пространственно-распределенные данные могут быть представлены в базе данных при помощи векторной или растровой моделей данных. Любая реальная географическая ситуация может быть представлена и векторной, и растровой модели. Данные из растровой могут быть конвертированы в векторную модель и наоборот.
В векторной модели пространственных данных графические данные представлены в виде объектов – точек, линий и регионов – с которыми связаны атрибутные данные. Координатами точек являются декартовы координаты в некоторой прямоугольной системе координат (например, в системе координат Гаусса-Крюгера) или географические координаты – широта и долгота. Линии или дуги представляются последовательностью точек. Структуры данных, основанные на векторном представлении, используются для кодирования сущностей, которые могут быть выделены как объект. В этих структурах объекты представлены в виде множества векторных примитивов, покрывающих лишь часть исследуемой территории.
Основным преимуществом "векторного" представления геоинформации является возможность описания топологических отношений между объектами. Это позволяет компактно представлять в памяти ЭВМ контурные объекты, сети, эффективно анализировать эти данные. Линейно-узловое топологическое представление основано на описании объектов в виде узлов, соединяющих их дуг и полигонов, образуемых дугами. Между элементами существуют топологические отношения, описываемые в виде таблиц смежности узлов и дуг, дуг и полигонов, смежности полигонов и т.п.
Растровые представления образуются путем соотнесения объектов с ячейками правильной геометрической формы, которые образуют регулярную сеть, покрывающую исследуемую территорию. Эти ячейки являются наименьшей единицей информации, их размеры могут в зависимости от приложения варьироваться от нескольких микрон до километров. Для привязки пиксела растрового изображения к пространственным координатам используется один из углов пиксела или его центроид. Каждая ячейка растра имеет дискретные атрибуты. Примерами использования растровой модели в ГИС являются данные дистанционного зондирования, полученные с ИСЗ, цифровые модели местности (DEM).
Основным преимуществом растровых представлений является совмещение позиционной и содержательной информации, что значительно упрощает реализацию алгоритмов анализа данных. Растровая модель является наиболее простой моделью представления пространственных данных. Растровые модели полностью покрывают исследуемое пространство и обеспечивают прямой доступ к информации о выделенном участке. Недостатком этих моделей является трудность представления геометрии объектов (точность представления зависит от разрешения сетки). Они требуют больших размеров памяти и ограничены в точности представления географических сущностей.
Для представления поверхностей в ГИС используются модели, основанные на разбиении компактного планарного домена карты на множество непересекающихся ячеек. Используются как регулярные разбиения, соответствующие растровой модели, так и нерегулярные – триангуляционные сети.
Геоинформационные системы предоставляют богатые возможности для обработки пространственно-распределенных данных: космических снимков, цифровых карт, триангуляционных и регулярных сетей. Функциональные возможности ГИС во многом определяются моделью данных. Первую группу функций составляют операции ввода пространственных и атрибутных данных. Ввод данных, имеющих координатную привязку, осуществляется при помощи дигитайзерной и сканерной технологии. Дигитайзеры применяются для оцифровки материалов, имеющих векторный характер, а сканеры – для ввода данных в grid-модели и для оцифровки изображений для автоматических векторизаторов. Средства ввода атрибутных данных в различных ГИС весьма разнообразны, однако большинство из них сводится к поддержке стандартных форматов обмена данными или драйверов внешних СУБД.
Функции обработки пространственных данных включают действия по преобразованию систем координат и трансформации картографических проекций, растрово-векторные преобразования, обработку данных дистанционного зондирования. Хранение позиционных и атрибутных данных в ГИС осуществляется в пространственной базе данных. Способ организации данных в системе во многом определяет ее функциональные возможности. Особенностью системы управления базой данных в ГИС является возможность обработки пространственных запросов.
Атрибутные данные в ГИС обеспечивают связь между местоположением символа и его значением. Этим символом может быть как ячейка матрицы в растровых ГИС, так и графический объект векторной ГИС. Связь осуществляется при помощи уникального номера пространственного объекта. Непространственные данные могут существовать в различных формах: в виде "плоского" файла, иерархической, сетевой или реляционной базы данных.
"Плоский" файл - самый простой способ хранения атрибутных данных. В "плоском" файле все свойства отображаемой географической сущности содержатся в одном файле в виде таблицы. Все записи об объектах имеют одинаковое число полей и фиксированную длину.
Обычно различают три класса баз данных: иерархические, сетевые и реляционные. Входящие в иерархическую модель записи образуют древовидную структуру – каждая из них связана с одной записью, находящейся на более высоком уровне иерархии. Доступ к любой из записей осуществляется путем прохода по строго определенной цепочке узлов дерева с последующим просмотром соответствующих этим узлам записей. Для простых задач иерархическая система эффективна, но она практически непригодна для использования в сложных системах с оперативной отработкой запросов и распределенной архитектурой. Иерархическая организация не может обеспечить быстродействие, необходимое для работы в условиях одновременного модифицирования файлов несколькими пользователями ГИС.
Сетевые модели устраняют некоторые недостатки иерархических моделей. Здесь каждый из узлов может иметь не один, а несколько узловродителей. Записи, входящие в состав сетевой структуры, содержат в себе указатели, определяющие местоположение других записей, связанных с ними. Такая модель позволила ускорить доступ к данным, но изменение структуры базы данных по прежнему требовало значительных усилий и времени.
Концепция реляционной модели данных была впервые выдвинута в 1950-е годы, но первые реализации появились только в 1970-х. СУБД реляционного типа освобождает пользователя от всех ограничений, связанных с организацией хранения данных и спецификой аппаратуры. Изменение физической структуры базы данных не влияет на работоспособность прикладных программ, работающих с нею. В распоряжение пользователя предоставляется простая структура данных – они рассматриваются как таблицы. Пользователь может не знать, каким образом его данные структурированы в базе – это обеспечивает независимость данных.
Аналитические возможности векторных ГИС включают как простые операции (измерения, оверлеи, буферы и скелетоны и т.п.), так и сложные операции: анализ сетей, выбор оптимального маршрута. Векторная модель данных подразумевает наличие для каждого объекта атрибутной составляющей, поэтому в таких ГИС обычно имеются возможности семантической выборки. Обязательным компонентом блока аналитических функций большинства современных ГИС являются операции топологического оверлея, определение принадлежности точки полигону, линии полигону и полигона полигону. В системах, поддерживающих описание межобъектной топологии, эти операции выполняются на порядки быстрее.
Простейший анализ в растровых ГИС основывается на "алгебре карт" и включает локальные, зональные, фокальные операции. Техника хранения, обработки и анализа данных в растровой модели типичны для компьютерной графики и цифровой обработки изображений. Аналитические возможности растровых ГИС простираются от простейших операций комбинирования нескольких слоев и вычисления различных статистических показателей до операций классификации, анализа соседства и т.д. Современные ГИС имеют возможности геометрической коррекции изображения – ортотрансформации и привязки к карте, генерализации, классификации изображений. Анализ поверхностей в ГИС представлен операциями вычисления углов наклона и экспозиций склонов, интерполяции высот, определения зон видимости, генерации горизонталей.
К числу функций вывода данных относятся воспроизведение
результирующих карт на экране графического дисплея, печать карт при помощи принтеров,
плоттеров. В последние годы популярным методом вывода информации ГИС конечному пользователю
является передача картографических изображений через Интернет.
Тема 2. Модель данных векторных ГИС
Окружающий нас мир слишком сложен для нашего непосредственного понимания. Мы создаем модели реальности, имеющие некоторые общие свойства с исследуемыми сущностями реального мира. На основе этих моделей создаются базы данных. Первоначально под словом “модель” подразумевался “образец в малом виде”, уменьшенная копия предмета. Впоследствии моделями стали называть любые образы (изображения, описания, схемы, карты и т.д.) объектов, процессов, явлений, используемые в качестве “заместителя”, “представителя”, оригинала данной модели.
Сущности реального мира в пространственно – распределенных базах данных представлены пространственными объектами, с которыми связаны атрибутные данные. Современные ГИС представляют пространственное распределение сущностей в виде объектов: точек, линий, ломаных, путей, площадей, поверхностей. Атрибуты содержат пространственную и непространственную информацию о сущностях и связаны с пространственными объектами.
Атрибут – свойство, качественный или количественный признак, характеризующий пространственный объект (но не связанный с его местоуказанием) и ассоциированный с его уникальным номером, или идентификатором. Наборы значений атрибутов обычно представляются в форме таблиц средствами реляционных СУБД. Классу атрибута при этом соответствует имя колонки, или столбца или поля таблицы. Данные в ГИС обычно разделяются на пространственную и непространственную составляющие. Различие между этими данными не является четким в силу наличия тесной взаимосвязи между ними.
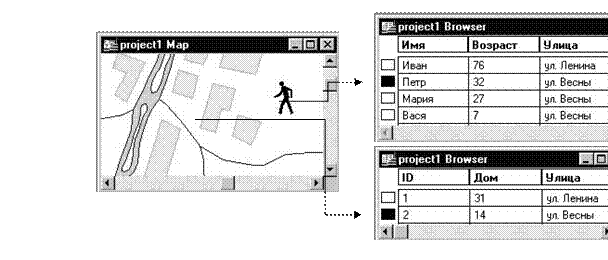
Рисунок 2.1 – Пространственные и атрибутные данные в ГИС
По степени сложности пространственные объекты подразделяются на элементарные (простые), составные и сложные. Элементарный объект имеет структурированное описание семантических и графических атрибутов, а также фактов и характера его взаимодействия с другими объектами. Составной объект имеет структурированное описание образованный группой других объектов с определенным (направленным) порядком их следования при образовании определяемого объекта. Сложный объект образуется группой других объектов (элементарных, составных, сложных), порядок следования которых при образовании определяемого объекта не фиксирован.
Выбор сущностей, которые будут отображены в модели точечными объектами, зависит от масштаба карты, изученности территории и т.д. Например, на крупномасштабных картах населенные пункты представлены точками, а на мелкомасштабных – площадными объектами.
Условия, при которых объект изображается в виде точки, могут быть выражены следующими положениями: пространственное расположение его важно; метрические размеры – не важны; размер объекта не выражается в масштабе модели. Точечные объекты – самый простой тип пространственных объектов. Координаты каждой точки могут быть представлены парой дополнительных столбцов базы данных. В этом случае каждая строка – точка, вся информация о точке заключена в строке, столбцы, не содержащие ординат, – атрибуты. Точки не зависят друг от друга.
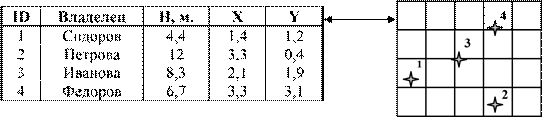
Рисунок 2.2 – Представление точечных объектов
Линейными объектами представляются сущности, “не имеющие ширины, а лишь протяженность”. Линейные данные часто называют сетями. Примеры сущностей, представляемых сетями: сети инфраструктуры, транспортные сети, линии электропередачи, газопроводы; естественные сети – речная сеть.
Объекты линейной сети состоят из узлов – мест, где линия заканчивается, прерывается, и дуг, соединяющих узлы. Узел – начальная точка или конечная точка дуги в векторно-топологическом представлении (линейноузловой модели) пространственных объектов типа линии или полигона. Узлы содержат атрибуты, устанавливающие топологическую связь со всеми замыкающимися в нем дугами. Дуга – последовательность сегментов, имеющая начало и конец в узлах; элемент векторно-топологических представлений линейных и полигональных пространственных объектов.
|
0-D |
Точка |
|
1-D |
Строка |
|
|
0-D |
Узел |
|
1-D |
Дуга |
|
|
1-D |
Отрезок |
|
1-D |
Направленная дуга |
|
|
1-D |
Сегмент |
|
1-D |
Цепочка |
|
Рисунок 2.3 – Элементы линейно-узлового представления сети
Валентность узла – число дуг, связанных с узлом. Окончание линии имеет валентность 1, узлы с валентностью 4 часто встречаются в дорожных сетях, а с валентностью 3 – в сети рек. Разновидностью сети является дерево, имеющее только один путь между парами узлов. Большинство речных сетей являются деревьями. Дуги могут иметь атрибуты, например: направление и объем трафика, время движения по дуге; Примеры атрибутов узлов: названия пересекающихся в узле улиц; количество трансформаторов на подстанции. Некоторые атрибуты связаны с частями дуг: например, часть железнодорожной ветки может проходить внутри тоннеля.
Границы контуров могут представлять различные природные феномены, такие, как озера, леса, крупные населенные пункты. Сущности являются изолированными областями, возможно перекрывающимися. Объекты могут не полностью покрывать исследуемую область (точка может находиться внутри нескольких объектов). Если каждая находится внутри одного объекта, объекты полностью покрывают территорию. Каждая линия границы разделяет два площадных объекта. Площадные объекты не могут пересекаться. Любой слой первого типа может быть преобразован в слой второго типа: каждый площадной объект может теперь иметь любое число атрибутов. Площадные объекты могут иметь «дыры», имеющие набор атрибутов, отличных от атрибутов основного объекта. Например, на реках есть острова.

Рисунок 2.4 – Сложные (многосвязные) площадные объекты
Некоторые явления и феномены, непрерывно изменяющиеся в пространстве, не могут быть точно представлены в виде дискретных точек, линий или областей – эти объекты наилучшим образом представляются в ГИС непрерывными поверхностями. Примеры непрерывных поверхностей: рельеф, температура, давление, плотность населения.
Характеристиками поверхностей являются критические точки: - пики и углубления – самые высокие и низкие точки;
- проходы – место схождения двух хребтов или низин; - дефекты – резкие изменения значения (например, утесы); - фронты - резкие изменения угла наклона поверхности.
Поверхности представляются в виде точек, линий и областей. Представление поверхностей в виде точек называется цифровой моделью местности и основано на выборке через регулярные интервалы значений с исследуемой поверхности. В результате получается матрица значений, называемая также растром, сеткой, решеткой. Многие цифровые модели местности создаются именно в таком виде и могут быть просто конвертированы в растровое изображение для визуализации.
|
|
|
Рисунок 2.5 – Представление поверхностей регулярной сетью точек
Представление поверхностей в виде линейных объектов идентично тому, что мы видим на топографических картах и основано на использовании изолиний (линий равных значений, например, высот). Линии соединяют выборочные точки, имеющие одинаковые значения атрибута.
Поверхности удобно также представлять площадными объектами. Чаще всего используют треугольники, так как эта фигура всегда выпуклая и лежит в одной плоскости. Представление поверхности набором треугольников называется триангуляцией. Выборочные точки являются вершинами треугольников, в сами треугольники полностью покрывают исследуемую территорию. Выборочные точки чаще всего располагаются в пиках и впадинах, вдоль линий хребтов и низин, и соединяются дугами.
При использовании непрерывных данных мы часто хотим знать значения атрибута вне точек, линий или вершин треугольника, представляющих поверхность. Эти значения вычисляются путем интерполяции по ближайшим точкам, в которых величина атрибута известна. Поверхности обычно обладают одним атрибутом, но иногда могут иметь несколько (например, многозональные космические снимки). Каждая ячейка имеет одно значение на всей описываемой ею площади.

Рисунок 2.6 – Представление поверхностей изолиниями и триангуляционной сетью
Векторная модель данных основана на векторах (в противоположность покрывающим все пространство растровым структурам). Фундаментальным примитивом является точка. Объекты создаются путем соединения точек прямыми линиями. Некоторые системы позволяют соединять точки дугами окружностей. Площадные объекты определяются как набор линий. Термин полигон является синонимом «площадного объекта» в силу использования прямых линий для соединения точек. Векторные базы данных создаются для различных целей: векторная модель доминирует в транспортных задачах, коммуникациях, управлении и т.д. Для управления ресурсами используются как векторные, так и растровые ГИС. В векторной базе данных объекты собираются в единое целое посредством топологии.
Топологические отношения в ГИС позволяют описывать связанность и отделимость точек или линий, определяющих взаимосвязи объектов в слое. Топологические отношения являются одним из наиболее полезных видов отношений, поддерживаемых пространственными базами данных. Топологическая структура данных определяет, где и как точки и линии соединяются в узлах на карте. Порядок соединения определяет форму дуги или полигона.
Рассмотрим пример кодирования топологических связей в ГИС и топологию «дуга-узел». После того, как векторизованы объект карты и построена топология, возможно определять связанность объектов, например, с какими полигонами соседствует полигон А, какой полигон граничит с полигоном Б через границу d, найти все возможные пути из третьего узла во второй.
Топология объектов может быть построена по «спагетти» следующим образом. Объекты и атрибуты позволяют описывать условия, существующие на карте или в реальности. Векторные объекты, используемые для описания пространственного изменения явления должны подчиняться правилам: два площадных объекта не должны перекрываться и каждая точка изучаемого пространства должна находиться внутри только одного площадного объекта.
|
1. Сохранение местоположения всех узлов, т.е. оконечных точек и точек пересечения линий или границ полигонов.
|
|
|
|
|||||||||||||||||||||||||
|
2. На основе этих узлов определяются дуги. Для этого указываются начальные и конечные точки дуги (узлы) и задается направление (начальный и конечный узел). Направление дуги позволяет определить маршрут между двумя узлами.
|
|
b |
|
|||||||||||||||||||||||||
|
3. Полигоны определяются дугами путем их перечисления по часовой стрелке вокруг объекта. Сохраняются дуги, составляющие полигон, порядок их следования и ориентация. Внутренние области (границы) полигона соответствующим образом помечаются (например, знаком «минус»).
|
|
|
b |
|
||||||||||||||||||||||||
|
4. Наконец, для каждой дуги можно определить, какой полигон находится слева и справаb от направления ориентации. Если дуга находится на границе изучаемой зоныc , соответствующая область помечается как «универсум» или внешний мир.
|
|
|
|
+ универсум Л – слева П – справа |
||||||||||||||||||||||||
Рисунок 2.7 – Кодирование топологических отношений в модели «дуга-узел»
Если редактируются точки объектов слоя, топология должна быть построена заново. Построение топологии включает в себя вычисление и кодирование взаимосвязей между объектами на основе планарных правил, использующихся для построения объектов по оцифрованным линиям. Планарные правила позволяют исправлять ошибки, возникающие при оцифровке.
Функции анализа в векторных ГИС отличаются от функций анализа растровых ГИС. Имеется больше возможностей для работы с отдельными объектами; в различных вычислениях, например, вычислениях площадей объектов, используются координаты объектов вместо подсчета количества ячеек в растровых ГИС. Это обуславливает большую точность вычислений. Некоторые операции выполняются быстрее (поиск оптимального пути в дорожной сети), а некоторые – медленнее (комбинирование слоев, буферные зоны).
Представим, что несколько слоев имеют построенную топологию (требуемую во многих ГИС, хотя и не во всех). Когда два слоя комбинируются (совмещаются), результат также должен удовлетворять условиям планарных правил. Для этого находятся все пересечения линий, и на каждом пересечении создается новый узел. Например, прямая, пересекающая выпуклый площадной объект, делит его на два полигона. Топологическое наложение – общее название для комбинирования слоев с использованием построенной топологической модели. Для получившейся в результате комбинирования слоев карты топологические связи обновляются.

Рисунок 2.8 – Комбинирование слоя линий и полигонов
При наложении полигонов их границы разбиваются на каждом пересечении объектов. Наложение линейных объектов на площадные также использует отношение “содержится в”. Линии разрываются на каждом их пересечении с границей полигона. Количество линий в результате этой операции становится больше. Содержащий линию полигон становится новым атрибутом каждой линии. Например, по карте на рисунке 2.8 можно определить ландшафт, по которому проходит каждый сегмент слоя дорог. Для наложения слоя точечных объектов на слой площадных объектов используется отношение «содержится в»., а результатом такой операции является новый атрибут для каждой точки. На рисунке 2.9 показаны две карты – точечный слой избушек и площадной слой видов ландшафта. В результате комбинирования этих слоев для каждого объекта в слое избушек получим вид ландшафта, на котором она расположена.

Рисунок 2.9 – Комбинирование слоя точек и полигонов
Операция переклассификации объектов применяется в работе с площадными объектами. В них объекты собираются вместе на основе атрибутов. Например, карта почв содержит объекты, имеющие атрибуты «тип почвы» (A, B, C) и «потенциал роста» (d и f). Чтобы получить карту по какому-то одному признаку, нужно объединить соседние объекты, имеющие одинаковые значения признака (рисунок 2.10), т.е. удалить границы между полигонами одного типа.


 Ad
Ad
а) б) в)
Рисунок 2.10 – Переклассификация объектов: а) – классификация объектов; б) – удаление границы между объектами одного типа; в) – сборка из дуг полигонов одного типа
Тема 3. Пространственные отношения в ГИС-анализе
ГИС предоставляют пользователю эффективные механизмы для хранения местоположения географических сущностей и их атрибутов, но кроме этого во многих задачах требуется проследить отношения между географическими объектами. Между объектами в векторной модели данных могут существовать пространственные отношения: близость, соседство, а также бинарные отношения "находится внутри", "находится снаружи", "пересекаются", "примыкает" и другие (рисунок 3.1).

Рисунок 3.1 – Пространственные отношения между объектами
Отношения между объектами могут быть вычислены на основе метрической информации об объектах. Например, язык создания приложений MapBasic в ГИС MapInfo позволяет выяснить взаимное расположение объектов в пространстве при помощи специальных географических операторов, встраиваемых в SQL-запрос.
Географические базы данных содержат множество пространственных данных, представляющих различные взгляды на окружающий мир в различные моменты времени. Термин пространственные означает, что объекты позиционированы в географическом пространстве. Пространственные объекты являются представлениями элементов реального мира – рек, городов, дорог и т.п. В зависимости от уровня детализации, эти объекты могут иметь различную пространственную размерность. Например, исток реки может быть выражен точечным объектом, ручьи – линейными объектами, а озера – полигональными объектами. Каждый пространственный объект описывается пространственными и непространственными атрибутами. Пространственные атрибуты, такие, как форма, размер, обычно складываются из позиционной и метрической информации об объекте. Пространственные объекты участвуют в пространственных отношениях, описывающих топологические свойства, такие, как связанность, ориентация, соседство, и вложенность.
Топологическая информация является неотъемлемой частью любой географической базы данных в геоинформационных системах и содержит пространственные отношения между объектами. Топологическая информация обычно хранится на уровне представления объектов. Например, представление линейного объекта может включать ссылки на другие связанные с ним объекты. В настоящее время топологические представления стали общепринятым методом организации геоданных в ГИС.
В модели топологических отношений Эгенхофера формализуются топологические отношения, которые могут существовать между двумя пространственными объектами. Такие топологические понятия, как смежность, вложенность и д.р., описываются совокупностью пересечений между внутренностями, границами и дополнениями двух элементов. Топологическое отношение R между двумя элементами A и B может быть задано матрицей:
Ao Bo Ao B Ao B
R(A,B) A Bo AB A B . (3.1)
o
A B A B A B
Значениями ячеек матрицы являются либо пустое значение , означающее, что сравниваемые внутренности, границы или дополнения не пересекаются, либо непустое значение , если в пересечении имеется хотя бы одна точка. Различные комбинации значений ячеек матрицы описывают 512 различных топологических отношений. Любое пространственное отношение между двумя элементами является инвариантом одного из отношений, описываемых матрицей. Однако на плоскости возможно реализовать лишь часть этих отношений (рисунок 3.2).
|
A не касается B
|
A касается B
|
A пересекает B
|
A содержит B
|
|||||||||
|
A эквивалентно B
|
A покрывает B
|
A содержится в B
|
A покрывается B
|
Рисунок 3.2 – Топологические отношения между двумя полигонами на плоскости
Если топологическое отношение между AX и BX в X эквивалентно топологическому отношению AY и BY в Y, то матрицы пересечений инвариантов для этих отношений будут идентичны. Обратное не верно, идентичность матриц пересечений инвариантов не означает эквивалентности отношений. Описанная модель топологических отношений полностью описывает пространственные отношения между объектами на уровне констатации факта отношения, но не содержит средств описания характера отношения. Например, если два региона касаются в двух точках, в модели будет зафиксирован только факт касания.
В векторных ГИС для передачи кодирование объектов используется модель данных “дуга–узел”, в которой полилинии и полигоны представляются в виде ориентированных графов. При этом фиксируются отношения инцидентности узлов и дуг, принадлежности дуги границе полигона, смежности полигонов. При векторизации карт векторные объекты представляют собой т.н. “спагетти”. Процесс преобразования спагетти в модель “дуга–узел” называется planar enforcement. Наличие в модели данных заранее рассчитанных топологических свойств объектов позволяет снизить вычислительную сложность многих алгоритмов.
В геоинформационных системах сложные алгоритмы анализа часто строятся из простых алгоритмов. Рассмотрим сначала некоторые простые алгоритмы, а далее покажем, как из этих простых алгоритмов строятся сложные аналитические процедуры.
Операция нахождение пересечения линий является одной из базовых в ГИС–анализе. Она используется в оверлейных операциях с полигонами, при соединении и разъединении (merge и dissolve) линий и полигонов. Эта операция является базисной при определении нахождения точки в полигоне, при удалении расщепленных полигонов. Поэтому эффективные алгоритмы определения пересечения линий важны в любой векторной ГИС.
Рассмотрим простейший пример: требуется определить, пересекается ли отрезок AB (4, 2) – (2, 0) с отрезком CD (0, 4) – (4, 0) и если да, то в какой точке? Для этого нужно найти уравнения прямых AB и CD и решить их совместно (рисунок 3.3-а). Уравнение прямой y=a+bx может быть найдено по двум точкам, через которые она проходит. Коэффициент наклона прямой b=(y2–y1) / (x2–x1). Используя любую из точек, через которые проходит прямая, найдем a=yi–bxi . Уравнение первой линии y=x–2, а второй линии y=4–x.
Сложив два уравнения, получим точку пересечения (3, 1).
В общем виде две линии,заданные уравнениями y=a1+b1x и y=a2+b2x, пересекаются в точке x = –(a1–a2) / (b1–b2); y = a1+b1x. Однако таким способом можно найти только точку пересечения непараллельных линий бесконечной длины. Возможно отрезки не пересекаются, а пересекаются продолженные по этим отрезкам прямые (рисунок 3.3-б). Отрезки пересекаются, если для точки пересечения (x, y) и точек A, B, C, D выполнены условия:
(xA– x)(x– xB) >= 0; (xC– x)(x– xD) >= 0; (3.2) (yA– y)(y– yB) >= 0; (yC– y)(y– yD) >= 0. (3.3)

0 2 4 0 2 4 а б
Рисунок 3.3 – Точка пересечения прямых: а) внутри отрезков; б) снаружи
Необходимо учитывать специальные случаи. Для вертикальных линий угол наклона b стремится к бесконечности, поэтому точку пересечения ищут особым способом. Если обе линии вертикальные, они не пересекаются. Если вертикальная только одна из линий, то подстановкой решается система уравнений y=const и y=a2+b2x. Невертикальные параллельные линии также вызывают сбой в работе алгоритма, поэтому перед решением системы уравнений следует проверять b1–b2 на равенство нулю.
Рассмотрим теперь способы определения пересечения полилиний. Пусть имеются две полилинии с n1 и n2 сегментами соответственно. Самым простым способом нахождения их точек пересечения является последовательная проверка пересечения каждого сегмента первой линии с каждым сегментом второй линии. Сложность этого алгоритма, пропорциональная произведению n1 * n2 , может быть уменьшена при помощи разнообразных эвристических алгоритмов. Хотя в этих алгоритмах требуются дополнительные шаги обработки и, возможно, структуры данных, общая трудоемкость алгоритма снижается. Рассмотрим некоторые из таких методов.
Сложность алгоритма вычисления пересечения полилиний может быть снижена, если предварительно проверять на пересечение минимальные ограничивающие прямоугольники полилиний (MBR – minimal bounding rectangle). Эти прямоугольники определяются минимальными и максимальными координатами x и y. Две полилинии не пересекаются, если не пересекаются их ограничивающие прямоугольники. Можно применить этот подход и для определения пересечения отдельных сегментов полилиний. Два отрезка AB и CD не пересекаются, если не пересекаются интервалы (xA, xB) и (xC, xD) или не пересекаются интервалы (yA, yB) и (yC, yD).
Следующий метод, впервые использованный в ГИС ArcInfo, основан на разбиении полилинии на секции, в которых линия монотонно возрастает или убывает по x и по y (рисунок 3.4-а). Разбиение происходит в точках локального минимума или максимума по x или по y. Горизонтальная или вертикальная линия пересекает такую секцию только в одной точке. Это дает возможность уменьшить трудоемкость алгоритма поиска пересечения полилиний. Если для двух секций найдена точка пересечения, не нужно проверять оставшиеся пары точек, т.к. это пересечение единственное при условии, что вторые производные в секциях не меняют знак. Это ограничение может быть разрешено либо разбиением секции в критических точках, либо полным перебором пар сегментов для таких секций. Модифицированный таким способом алгоритм в некоторых случаях позволяет получить вычислительную сложность порядка O(n1 + n2).
На рисунке 3.4-б представлены два различных случая пересечения секций. В одном случае секции пересекаются только в одной точке, в другом – в нескольких точках. Определим условия, при которых точка пересечения единственна. Если две секции одновременно возрастают или убывают по одному направлению, одна из них возрастает, а другая убывает по другому, то полилинии на этих секциях пересекаются не более чем в одной точке. На рисунке 3.4-в серым цветом выделены условия, при которых можно применять вышеописанный метод оптимизации алгоритма поиска пересечений полилиний.
|
|
x возр. y возр. |
x возр. y убыв. |
X убыв. y возр. |
x убыв. y убыв. |
|
x возр. y возр. |
|
|
|
|
|
x возр. y убыв. |
|
|
|
|
|
x убыв. y возр. |
|
|
|
|
|
x убыв. y убыв. |
|
|
|
|

 б)
б)
а) в)
Рисунок 3.4 – Оптимизация алгоритма пересечения полилиний, основанная на разбиении на монотонные секции: а) разбиение на секции; б) различные варианты пересечения секций; в) схема определения единственности точки пересечения секций
Если требуется найти точки пересечения большого числа полилиний, как, например, в оверлейной задаче, можно организовать пространственную индексацию полилиний. Наиболее часто в ГИС используются индексы на квадродеревьях. При такой индексации поиск пересечений ведется только для полилиний, у которых ветви квадродерева пересекаются.
Перейдем теперь к операциям с полигонами, заданными последовательностью вершин. Рассмотрим задачу определения площади полигона. Чаще всего применяется алгоритм, основанный на разбиении многоугольника на трапеции, ограниченные линией сегмента полигона, перпендикулярами, опущенными из вершин сегмента на ось x, и осью x (рисунок 3.5-а). Для сегмента, соединяющего вершины (xA,yA) и (xB,yB), площадь такой трапеции равна S=(xB– xA)* (yB– yA) / 2.
Вычислим площади трапеций для всех сегментов полигона и просуммируем их. Для сегментов, у которых xi > xi+1, площадь берется отрицательной (рисунок 3.5-б). Следует заметить, что полигон – замкнутая фигура, поэтому нужно учитывать сегмент, соединяющий последнюю вершину с первой.

Рисунок 3.5 – Вычисление площади полигона: а) исходная фигура;
б) разбиение на трапеции
Таким способом можно вычислить площади не только для выпуклых многоугольников, но и для вогнутых, а также для полигонов, имеющих дыры. Алгоритм непригоден для вычисления площадей полигонов, имеющих самопересечения границ. Для полигонов, оцифрованных против часовой стрелки, площадь получается отрицательной. Проблемы возникают также при отрицательных значениях координат y вершин полигона. В таком случае можно либо прибавить к координатам y достаточно большое число, либо опускать перпендикуляры из вершин на прямую y=const, где const меньше самой малой y-координаты в полигоне.
Если используется система координат с большими значениями x и y (например, в системе координат Гаусса-Крюгера в районе Красноярска действуют координаты x=6200000; y=16500000), то при многократном суммировании площадей трапеций будет накапливаться вычислительная ошибка. Относительная погрешность получается особенно высокой для малых полигонов. Эта проблема может быть решена линейным преобразованием полигона к новой системе координат, в которой не будет столь больших значений, и вычислением в ней площади. Далее вычисляется площадь в исходной системе.
В модели “дуга-узел” полигоны формируются из дуг. При этом кодируется расположение полигона относительно направления цифрования дуги. Очевидно, определяемую границей двух смежных полигонов площадь достаточно вычислить один раз. Затем для правых полигонов эта площадь суммируется со знаком “плюс”, а для левых – со знаком “минус”.
Рассмотрим следующую задачу, часто встречающуюся в процедурах ГИС-анализа. Для заданной точки A(u, v) и полигона P=(xi, yi) i=1..n требуется определить, находится точка внутри полигона или снаружи. Задача может быть решена с использованием топологических свойств полигонов. Из точки A проведем вертикальную линию (xi, yi) – (xi, ) и вычислим количество пересечений этой линии с сегментами границы полигона. Если это число нечетное, точка лежит внутри полигона. Если число четное – точка лежит вне полигона (рисунок 3.6).

Рисунок 3.6 – Схема определения принадлежности точки полигону.
Вертикальная линия x=u пересекает сегмент с концевыми точками (xi, yi) и (xi+1, yi+1) когда эти точки расположены по разную сторону от вертикальной линии. Уравнение прямой сегмента y=a+bx определяется по его концевым точкам, а пересечение сегмента с вертикальной прямой x=u находится в точке (u, a+b*u). Вертикальные сегменты границы являются для этого способа определения принадлежности точки полигону специальным случаем. Когда xi=xi+1 и xi<>u, линия и сегмент границы не пересекаются. Когда xi=xi+1 и xi=u, прибавим к количеству пересечений 0 или 2. Для сохранения детерминированности алгоритма нужно также проверять, расположена ли точка на границе полигона (a+b*u=v). Иначе алгоритм в разных случаях будет выдавать разные результаты (рисунок 3.7).

 2 пересечения 3 пересечения Точка снаружи
Точка внутри
2 пересечения 3 пересечения Точка снаружи
Точка внутри
Рисунок 3.7 – Неопределенность при расположении точки на границе
Если граница полигона разбита на монотонные секции, вертикальная линия пересекает секцию не более чем в одной точке. Поэтому когда найдено одно пересечение, можно не проверять оставшиеся сегменты секции на пересечение с вертикальной линией. Алгоритм можно применять также и вогнутых полигонов, для полигонов, имеющих дыры и самопересечения границ.
Перейдем к задаче определения центральной, репрезентативной точки полигона. В ГИС с этой целью часто используется понятие центроида – точки, являющейся центром тяжести полигона. Как видно из рисунка 3.8, центроид расположен не всегда внутри полигона. Однако эта операция может применяться, например, в картографической генерализации при замене площадных объектов точечными.

Рисунок 3.8 – Расположение центроидов полигонов.
Координаты центроида региона с площадью A вычисляются по сле-
дующим формулам: xц= ((yi – yi+1) (xi2 + xi xi+1 + xi+12) / 6A); yц= ((xi – xi+1) (yi2 + yi yi+1 + yi+12) / 6A). В некоторых программах координаты центроида вычисляются как среднее значение x и y.
Рассмотрим следующую полигональную операцию – вычисление скелета полигона. Скелет полигона определяется как сеть линий, построенная таким образом, что каждая точка сети расположена на равном расстоянии от ближайших двух сегментов границы полигона. При помощи этой операции можно определить оптимальные места для подписи полигона. Скелет получается путем “сжатия” полигона (рисунок 3.9). Сегменты границы полигона сдвигаются внутрь полигона на равные расстояния, поэтому можно считать эту операцию обратной построению буфера.
Выпуклые вершины многоугольника сдвигаются внутрь в направлении биссектрисы угла, формируемого смежными с вершинами сегментами. Вогнутые участки в скелете полигона заменяются дугами окружности. Правильные многоугольники превращаются в точки, являющиеся центрами вписанных окружностей.

Рисунок 3.9 – Схема получения скелета полигона.
Наложение картографических слоев является основным средством для реализации сложных пространственных отношений, называемых в англоязычной литературе spatial join. Геометрические аспекты оверлея тематических слоев основаны на методах вычислительной геометрии. Однако в пространственных запросах не только вычисляются пересечения объектов на входных картах, но и выполняется комбинирование их атрибутов.
Оверлеи слоев в растровых форматах сводятся к комбинированию значений соответствующих ячеек. Такие операции достаточно просты и не требуют использования методов вычислительной геометрии. Для выравнивания растров, имеющих различную ориентацию или размер ячеек, могут использоваться различные алгоритмы трансформации.
В векторных ГИС встречается несколько типов оверлейных операций: оверлеи двух разбиений (например, регионов), оверлеи двух линий, оверлеи линии и региона, оверлеи точки и региона. Для оверлеев типа "регионрегион" и "линия-регион" входные данные могут представлять собой результат предыдущих оверлейных операций. Картографический оверлей сводится к нескольким стандартным задачам: поиску точек пересечения двух сегментов, удалению расщепленных полигонов, вычислению пересечений двух разбиений, определения принадлежности точки региону.
Простые алгоритмы, рассмотренные в предыдущих разделах, формируют базис для более сложных алгоритмов ГИС-анализа, таких, как оверлеи полигонов. Эта операция традиционно используется в ландшафтном планировании, где с целью управления использованием земель исследуются пространственные взаимосвязи между наложенными друг на друга географическими слоями.
Оверлеи полигонов изоморфны операциям теории множеств. Когда накладываются два полигона A и B, получается графическая интерпретация объединения или пересечения множеств A и B. На рисунке 3.10 показаны 16 возможных оверлейных операций с двумя полигонами, выраженные через объединение, пересечение и отрицание помеченных цифрами 1 .. 4 множеств.
На основе оверлейных операций строятся некоторые другие функции ГИС.
При визуализации данных интерес представляют только объекты, попадающие в “окно” пользователя, а остальные объекты для ускорения отображения должны быть пропущены. Для этого на слои карты накладывается прямоугольник – экстент карты, вне которого объекты не отображаются. При построении буферов вокруг точек, полилиний и полигонов создаются круги и прямоугольники, которые впоследствии оверлейной операцией сливаются в один объект.
Оверлейные операции применяются при площадной интерполяции. Здесь требуется распределить некоторую величину, связанную с полигоном A, между пересечением A B и разностью A – B пропорционально их площади. При этом считается, что плотность этой величины по всему полигону постоянна.

Рисунок 3.10 – Связь оверлеев полигонов с операциями теории множеств.
Перейдем теперь к способам реализации оверлейных операций. Будем рассматривать наиболее распространенный в ГИС-анализе случай, когда накладываются два слоя с непересекающимися полигонами. Представим, что в одном из слоев содержатся “красные” полигоны, а в другом – “синие”. Тогда задача заключается в поиске полигонов на комбинированном слое. Атрибуты этого слоя содержат конкатенацию характеристик “синих” и “красных” полигонов. Количество полигонов, получившихся в результате наложения слоев, заранее предсказать нельзя.
Чтобы получить оверлей двух полигонов, вначале необходимо вычислить все пересечения между их границами. На рисунке 3.11 изображен “красный” полигон с атрибутом “A” (тонкие линии) и синий полигон с атрибутом “1” (толстые линии). Внешняя часть на обеих картах имеет атрибут “0”. Каждый полигон представлен одной дугой, для каждой из них известно, с какой стороны расположен полигон. После вычисления пересечений этих дуг образуются шесть новых дуг и четыре новых полигона, наследовавших атрибуты 00, A0, A1, 01. Для новых дуг также известно, какие полигоны лежат справа и слева. По таблице смежности получившихся дуг и полигонов можно сформировать любой из возможных шестнадцати полигонов, показанных на рисунке 3.11.

a) б)
Рисунок 3.11 – Оверлей полигонов в модели “дуга–узел”: а) исходные объекты;
б) вычисление пересечений дуг; в) метки смежности дуг и полигонов.
Рассмотрим более сложный пример (рисунок 3.12). Здесь накладываются слой с объектом “1” и слой с тремя объектами “A”, “B” и “C”. Вычислим пересечения дуг объектов и получим метки правых и левых полигонов получившихся новых дуг.

Рисунок 3.12 – Оверлей полигонов с непересекающимися границами.
Как видно из рисунка, дуги 3, 6 и 8 не имеют пересечений с объектом “1”. Определим метки для третьей дуги. Легко видеть, что метки внутри полигона могут передаваться от дуги к дуге. Правый полигон третьей дуги тот же, что правые полигоны второй и четвертой дуги – “А1”. Левый полигон шестой дуги тот же, что левые полигоны второй и четвертой дуги – “А1”. Для третьей дуги, как для части сети “красного” слоя, известна “красная” часть метки левого полигона – это “B”. “Синяя” часть левой метки берется из метки правого полигона. В результате получается метка “B1”. Аналогично, метка правого полигона для шестой дуги будет “B1”.
Восьмая дуга не пересекается с границей полигона “1” и не является смежной с другими дугами сети “красного” слоя. Для изолированной дуги при помощи алгоритма “точка в полигоне” следует определить вмещающий полигон “синего” слоя. Получим для восьмой дуги правый полигон “С1” и левый полигон “01”. Последний шаг оверлейного алгоритма заключается в формировании полигонов из новых дуг путем обхода полигона от дуги к дуге до тех пор, пока полигон не замкнется.
Точность представления координат сегментов в машинной форме более высока, чем погрешности оцифровки и векторизации. Поэтому при поиске пересечений сегментов полигона могут возникать ошибки, связанные с отсутствием сведений о топологической структуре объектов. На рисунке 3.13 показаны два различных случая пересечения линий.


 а)
а)
б)
Рисунок 3.13 – Проблемы поиска пересечения полигонов:
а) пересекающиеся сегменты; б) ложные пересечения сегментов смежных полигонов; в) расщепленные полигоны.
Из рисунков видно, что в первом случае линии пересекаются на самом деле, а во втором случае пересекающиеся участки линий представляют одну и ту же границу. Необходимо составлять оверлейные алгоритмы таким образом, чтобы различать эти ситуации. Полигоны, образующиеся при оверлее двух полигонов с ошибочно векторизованными общими границами, называются расщепленными. Для двух полигонов, состоящих из n1 и n2 точек, может образоваться до ( 2n1n 2/ (n1+n2) – 3 ) расщепленных полигонов.
Расщепленные полигоны могут быть устранены либо в процессе оверлейной операции, либо после ее выполнения. В большинстве коммерческих ГИС используется первый подход, заключающийся в “нечетком” представлении линий. При этом для каждой линии задается уровень толерантности, связанный с возникающей из-за ошибок векторизации неопределенностью геометрии линии. Поиск пересечений ведется для “полос”, заданных самой линией и уровнем толерантности (рисунок 3.14-а). Следует заметить, что определение пересечений для нечетких линий не является транзитивным.

![]() 2 A
2 A
а) б)
Рисунок 3.14 – Удаление расщепленных полигонов: а) до оверлейной операции;
б) после оверлейной операции
Для устранения расщепленных полигонов после оверлейной операции необходимо определить критерии, по которым расщепленный полигон можно отличить от настоящего. Расщепленные полигоны обычно имеют небольшую площадь и вытянутую форму. Они чаще всего состоят из двух дуг. Расщепленные полигоны характеризуются также “перемежающимися” атрибутами. Если синяя дуга с атрибутами “1” и “2” накладывается на “красную” дугу с атрибутами “A” и “B”, расщепленные полигоны будут иметь атрибуты “B1” и “A2” (рисунок 3.14-б). Дуги расщепленных полигонов заканчиваются в четырехвалентных узлах, а в реальных полигонах валентность узлов обычно равна трем. Состоящий из двух дуг расщепленный полигон можно заменить одной дугой, проходящей через центр полигона.
Тема 4. Ввод пространственных данных в ГИС
Географические явления и феномены бесконечно сложны и разнообразны. Для того, чтобы абсолютно полно представить их в ГИС, потребовались бы бесконечно большие пространственные базы данных. Чтобы описывать, обрабатывать и анализировать объекты реального мира в ГИС, используют модели данных, в которых абстракцией и агрегацией данных устанавливается необходимый для решения поставленной задачи уровень детальности информации. Это касается как атрибутной, так и пространственной составляющих геоданных. На географических картах уровень детальности информации определяется масштабом карты. Здесь в качестве примера абстракции данных можно привести процесс камерального создания мелкомасштабных карт на основе крупномасштабных путем их генерализации. Пользователь ГИС смотрит на окружающий мир через модель пространственных данных, которая должна с достаточной полнотой и точностью описывать объекты и явления.
Изображения объектов и явлений на географических картах и космических снимках обычно описываются функцией двух переменных F(x,y), где x,y – географические координаты. Аналитический способ определения функции F(x,y) с целью определения пространственного положения географических объектов практически не применяется. Вместо этого функцию F(x,y) сэмплируют – т.е. представляют выборочными значениями в некоторых точках (их называют выборочными точками).
Способ дискретизации функции F(x,y) определяет модели данных ГИС: растровые модели, DLG-графы векторных ГИС, модели поверхностей TIN и DEM. Представление феноменов и явлений объективной реальности выборочными значениями и кодирование этих значений в пространственной базе данных называется вводом данных в ГИС.
Большая часть характеристик географических объектов и явлений существует на всей территории и изменяется непрерывно (рельеф территории, температура, атмосферное давление и т.п.). Если взять выборочные точки в узлах регулярной решетки, получим растровую модель данных. Размещение точек вдоль трансект либо вдоль границ объектов порождает векторную модель (в виде полилиний и полигонов), а изображение объектов и явлений в изолиниях приводит к 3D-моделям.
Феномены окружающего мира могут быть рассмотрены в трех аспектах: пространственном (вариации значений от одного места на карте до другого), временном (изменения между двумя моментами времени) и тематическом (вариации от одной характеристики до другой). Измеряемые или описываемые свойства объектов попадают в одну из этих категорий, и их полное описание во всех трех аспектах практически невозможно. При построении ГИС-моделей одна из категорий фиксирована, другая – контролируется, а третья – свободно изменяется. Например, при переписи населения фиксируется время (год переписи), контролируется местоположение, используя census track, и измеряется разная тематическая информация (возраст, пол и т.п.).
Ввод данных – наиболее узкое место в геоинформационных технологиях. Затраты на ввод данных часто превосходят 80% от общей стоимости ГИС-проекта. Процесс ввода данных обычно требует участия большого количества операторов, сами операции ввода – утомительны (однообразная, рутинная работа), требуется постоянно контролировать ошибки ввода данных. Поэтому для снижения трудозатрат и стоимости ввода и для повышения качества ГИС-продуктов нужно автоматизировать процессы ввода данных, насколько это возможно.
В ГИС используется несколько режимов ввода данных. Путем ручного ввода (например, с клавиатуры) могут быть введены табличные данные, элементы оформления и дизайна карты, реже пространственные данные (из-за их большого объема). Ручные устройства определения координат, при помощи которых оператор непосредственно указывает местоположение географического объекта и фиксирует его координаты, позволяют оцифровывать карты, выполнять ручное дешифрирование снимков. Автоматизированные устройства ввода автоматически извлекают геоданные с карт и снимков. В настоящее время производители ГИС пытаются использовать для ввода данных новые технологии, например, голосовой ввод, но в общераспространенном программном обеспечении ГИС эти возможности пока недоступны.
Данные для ГИС-проекта могут быть также получены из других ГИС и CAD/CAM – систем; в этом случае ввод данных сводится к преобразованиям между различными ГИС-форматами. Существуют специальные обменные форматы для передачи пространственных данных между разными ГИС (DFX/DBF, MIF/MID и т.п.). Современные попытки разработки стандартов на пространственные данные и на процедуры обмена базируются на XML.
Одним из способов снижения затрат на ввод данных является также разделение цифровых данных (data sharing), когда несколько коллективов, занятых разработкой ГИС, совместно создают, владеют и используют банк геопространственных данных, что позволяет избежать ситуаций, когда две организации тратят ресурсы на ввод одинаковых карт. Кроме того, сейчас в сети Интернет появляется все больше свободно доступных пространственных данных (космические снимки и цифровые карты GoogleEarth, цифровые модели местности NASA и многое другое).
Для ввода данных в ГИС необходимы технические и программные средства преобразования пространственных данных различных типов в цифровую форму. Пространственные данные кодируются в виде списка координат, а атрибутные данные чаще всего представлены в виде таблиц. Для пространственных данных часто требуются преобразования между различными проекциями и системами координат цифровой карты, космического снимка и т.п.
Первыми устройствами для аналого-цифрового преобразования картографической информации в ГИС были дигитайзеры – устройства ручной оцифровки карт, схем и планов в виде последовательности точек, положение которых описывается прямоугольными декартовыми координатами плоскости. Дигитайзер состоит из плоского стола и указующего устройства – съемника информации в виде курсора или пера. Рабочее поле стола может быть выполнено из прозрачного материала и иметь подсветку. Дигитайзеры различаются размером рабочего поля (форматы А4–А0), точностными характеристиками: точностью (accuracy), контролируемой погрешностью курсора, точностью поля дигитайзера, конструктивным разрешением (величиной минимального шага – инкремента). Интегральная точность современных дигитайзеров обычно лежит в пределах сотых или десятых долей миллиметра.
Первые дигитайзеры создавались в начале 1960-х на базе светостолов – столов со столешницей из прозрачного материала, под которой был размещен источник света. Оператор перемещал по закрепленной на столе карте курсор, внутри которого располагался электромагнит. Магнитное поле, создаваемое курсором, движет расположенный под столом кулачок. Механические перемещения кулачка вдоль осей oX и oY кодировались и передавались в ЭВМ, где специальная программа формировала из этих перемещений векторные полилинии и полигоны.
Первые электромеханические дигитайзеры были механически связанными; дигитайзеры со свободным перемещением курсора были очень дороги и нестабильны в работе. Так, в одном из первых дигитайзеров со свободным перемещением курсора курсор генерировал звук, который фиксировался линейкой микрофонов. Дигитайзер выдавал много ошибок из-за проблем с шумами.
В современных дигитайзерах чаще всего используется решетка катушек, спрятанная в столе и детектирующая электромагнитное поле, генерируемое курсором. По величине ЭДС, наведенной в каждой из катушек, процессор дигитайзера определяет положение курсора с точностью лучше 0,1 миллиметра (эта точность выше, чем точность позиционирования курсора любым оператором). Во многих дигитайзерах функция географической привязки изображения по реперным точкам заложена в само устройство или в его драйвер.
Рассмотрим процесс ввода карты в ГИС при помощи дигитайзера. Сначала карта фиксируется на столе: при сдвиге карты привязку нужно проводить заново. Карта должна плотно прилегать к поверхности стола, иначе неизбежно возникают ошибки геопривязки изображения. Для привязки снимаются координаты трех реперных точек – этого достаточно, если используются аффинные преобразования, и есть уверенность в точности определения координат реперных точек. Для контроля ошибок при определении координат или если используется функция преобразования координат более высокого порядка, оператору потребуется определить большее количество реперных точек.
Реперные точки удобно брать в местах пересечения дорог, на углах зданий, в устьях рек и т.п. Для каждой реперной точки должны быть известны её координаты в системе координат дигитайзера (обычно задаются в виде расстояния от края рабочего поля) и в системе координат оцифровываемой карты. Координаты реперных точек используются для вычисления параметров функции трансформации координат.

Рисунок 4.1 – Сканеры: а) – планшетный; б) – барабанный
 Сканеры – устройства аналого-цифрового
преобразования изображения для его ввода в ЭВМ в растровом формате путем
сканирования в отраженном или проходящем свете с непрозрачного и прозрачного
оригинала (рисунок 4.1). Видеосканеры (телекамеры, светочувствительные матрицы)
позволяют менее чем за 1 сек. получать полностью сканируемое изображение, формируя
растровый массив значений яркостей, цвета. Полученное при помощи видеосканера изображение
содержит значительные геометрические искривления, что затрудняет использование видеосканеров
для ввода карт.
Сканеры – устройства аналого-цифрового
преобразования изображения для его ввода в ЭВМ в растровом формате путем
сканирования в отраженном или проходящем свете с непрозрачного и прозрачного
оригинала (рисунок 4.1). Видеосканеры (телекамеры, светочувствительные матрицы)
позволяют менее чем за 1 сек. получать полностью сканируемое изображение, формируя
растровый массив значений яркостей, цвета. Полученное при помощи видеосканера изображение
содержит значительные геометрические искривления, что затрудняет использование видеосканеров
для ввода карт.  а
а
)
Рис 4.2. – Устройство сканеров: а) – барабанных; б) – планшетных (www.pcmore.ru)
Электромеханические сканеры, более дорогие и более медленные, чем видеосканеры, выдают более качественные изображения. Эти сканеры разделяют на планшетные, барабанные и ручные. В планшетных сканерах (рисунок 4.2-а) над неподвижной картой перемещается источник света и линейка светочувствительных элементов, фиксирующих яркость отраженного от карты света. В барабанных сканерах нерах (рисунок 4.2-б) наоборот – над неподвижным источником света и линейкой светочувствительных элементов «прокатывается» карта. Ручные сканеры, перемещаемые над сканируемым документом вручную, в ГИС используются крайне редко из-за низкой позиционной точности результата и малого формата документа, который можно отсканировать за один проход.
Оцифровку содержимого карты можно производить в точечном режиме, когда оператор устанавливает точки явно нажатием кнопки на курсоре, или в потоковом режиме, при котором положение точек снимается автоматически через некоторый промежуток времени (обычно 0,1–1 сек.) или при движении курсора на заданное количество позиций. В точечном режиме точки выбираются субъективно; два оператора никогда не оцифруют одну и ту же ломаную одинаково. Но оператор в этом режиме может размещать точки более правильно, т.е. чаще ставить точки на изгибах линий и реже – на прямых участках. В потоковом режиме точки размещаются независимо от формы кривой, поэтому создается много избыточных точек, которые нужно отфильтровать.

Рисунок 4.3 – Влияние особенностей картографического изображения на процесс векторизации
Большая часть существующих бумажных карт создается без учета того, что когда-нибудь их будут оцифровывать, поэтому при оцифровке карт неизбежно возникают проблемы. Часто на картах в целях более наглядного изображения географических объектов жертвуют их позиционной точностью. Например, по узкой береговой полосе проходят ЛЭП, автомобильная и железная дороги (рисунок 4.3). Если вынести эти объекты на карту точно по тем координатам, где они расположены, три линии могут слиться в одну. В этом случае эти линии рисуют на небольшом расстоянии друг от друга, пренебрегая позиционной точностью и сохраняя топологию объектов. Если граница территорий проходит по естественным объектам (по реке, не выраженной в масштабе карты по ширине), линию границы изображают поочередно на разных берегах этой реки.

Рисунок 4.4 – Типичные ошибки оператора при оцифровке карты
Планшет топографической карты, основной источник данных для создания цифровых карт, является самостоятельным картографическим произведением. В геоинформационных системах планшеты цифровых карт часто используются совместно с целью создания топографических основ какойлибо территории, например, административного района или края в целом. Для решения этой задачи необходимо совмещение тополого-метрической информации на границах планшетов.
Совместное использование планшетов цифровых топографических карт в системе координат Гаусса–Крюгера требует пересчета координат в одну зону. Но даже после этого метрика объекта, пересекающего границы планшета, будет разорвана. Величина расхождения в метрике чаще всего лежит в пределах картографической точности, поэтому корректной будет операция по усреднению метрики объектов на стыках листов. Эта операция называется "сводкой" планшетов топографических карт (рисунок 4.5).

а) б) в)
Рисунок 4.5 – Сводка топографических планшетов: а) – выделение объектов, имеющих выход на границу листа; б) – поиск пар, представляющих один объект на местности; в) – усреднение метрики сводимых объектов.
Сводка планшетов сводится к выполнению ряда простых операций. В зависимости от расположения сводимых листов задается широта или долгота сведения. Задается критерий близости объектов – минимальное расстояние между вертексами линейных объектов на соседних листах, при котором они считаются различными. Алгоритм сводки состоит в последовательном сравнении с критерием близости расстояний между вертексами всех элементах декартового произведения множеств объектов двух сводимых листов (рисунок 4.5). Чтобы не перебирать все пары объектов, по заданной ширине полосы сведения выбираются объекты, имеющие выход на границу со сводимым листом. В результате получим множество пар объектов, вертексы которых находятся достаточно близко друг от друга, чтобы считать эти объекты изображением одного предмета. Если расстояние между вертексами объектов не превосходит точности карты, их можно свести без ошибок в одну точку.
Под картографической генерализацией понимают процесс обработки картографического изображения, осуществляемый посредством абстрагирования и содержательного обобщения объекта в соответствии с масштабом и назначением карт. Цифровые карты крупных масштабов являются источником данных для создания мелкомасштабных карт, применяемых для печати обзорных карт небольших форматов. Мелкомасштабные карты создаются путем генерализации исходных цифровых карт.

|
замена масштабного изображения внемасштабным изображением |
генерализация геометрии картографических объектов |
![]()
![]() исходная
цифровая карта сокращение объектного состава карты и удаление мелких
объектов
исходная
цифровая карта сокращение объектного состава карты и удаление мелких
объектов
Рисунок 4.6 – Генерализация карты масштаба 1 : 1 000 000
В ГИС понятие генерализации задается в более обобщенном виде – как редукция "информационной плотности" в пространственной базе данных, при которой сохраняется ее общая структура и семантика. Процесс генерализации в ГИС сложен и требует больших вычислительных затрат. Высокая вычислительная сложность машинной генерализации объясняется тем, что в этом процессе учитываются как геометрические аспекты географических сущностей – форма, структура, детализация, так и негеометрические – роль и важность объекта в контексте карты (рисунок 4.6).
В настоящее время в литературе встречаются работы по моделированию отдельных стадий этого процесса. Достижение полной автоматизации этого процесса невозможно по причине бесконечного многообразия отношений между объектами и явлениями. Наиболее изученная часть проблемы – упрощение геометрии объектов. Здесь самым известным и часто используемым алгоритмом возможно является эвристический алгоритм Дугласа и Пекье для простой открытой полигональной цепи.
На мелкомасштабных картах отображается обзорное представление картографируемого объекта или явления. Для этой задачи мелкие детали, имеющиеся на картах более крупного масштаба, только препятствуют комплексному взгляду на предмет. Поэтому при создании карт мелких масштабов на исходной карте выделяются наиболее общие классы объектов: реки, озера, крупные населенные пункты, автомобильные и железные дороги.
Содержательная разгрузка карты выполняется также путем удаления мелких объектов. С исходной карты удаляются линейные объекты, длина которых меньше некоторой величины, определяемой масштабом карты. Таким же способом – выборкой по площади – удаляются мелкие полигональные объекты.
При уменьшении масштаба объекты могут менять свою пространственную локализацию. Площадные объекты, которые в новом масштабе не выражаются по одному из направлений, заменяются линейными объектами. Если площадной объект перестает выражаться по всем направлениям, то он заменяется точечным. Линейный объект заменяется точечным, если его длина перестает выражаться в масштабе карты (рисунок 4.7).
Агрегация предполагает переход от частных понятий к общим понятиям и контролируется в основном негеометрическими правилами. Группа близко расположенных объектов при уменьшении масштаба может быть выражена единым условным знаком, обозначающим некоторое собирательное понятие.
Геометрическая сторона картографической генерализации алгоритмически наиболее сложна. Для разных типов объектов решение задачи генерализации будет своим. Однако, можно выделить общие операции, которые применяются при генерализации картографических объектов: замена ломаной отрезком при заданном предельном угле излома, удаление точек, лежащих на одной прямой, объединение нескольких условных знаков один, замена масштабного изображения внемасштабным (рисунок 4.7-г).
![]()
![]()

а) б)

в) г)
Рисунок 4.7 – Генерализация объектов: а) – замена ломаной линии прямой при заданном предельном угле излома; б) – замена масштабного изображения внемасштабным знаком;
в) – удаление точек, лежащих между близкими параллельными прямыми; г) – объединение нескольких условных знаков
Существует несколько алгоритмов генерализации полилиний. Алгоритмы, независимые от формы линии, наиболее просты – в них просто удаляется заданное количество точек (например, удаление каждой точки), но генерализируют форму линии очень грубо и могут порождать топологические ошибки.
В локальных алгоритмах чтобы определить, оставить текущую точку или нет, используются характеристики соседних точек. Линейные и площадные объекты цифровой карты описываются последовательностью точек, которые должны быть расположены достаточно близко, чтобы обеспечить плавность линии при визуализации в исходном масштабе карты. В мелком масштабе плавность линий обеспечивается меньшим числом точек. Поэтому ломаная на участках, имеющих небольшой угол излома, заменяется прямой линией. Если несколько идущих подряд точек лежат на одной прямой, они не несут информации и удаляются.

а) б)
Рисунок 4.8 – Генерализация полилинии алгоритмом Дугласа-Пекье: а) – определение самой дальней точки от прямой; б) – рекурсия
В глобальных алгоритмах генерализации полилиния рассматривается целиком. Типичным примером глобальной генерализации, нашедшим применение во многих современных ГИС-пакетах (в частности, в ГИС ArcInfo), является алгоритм Дугласа-Пекье. Рассмотрим его работу (рисунок 4.8).
![]() Сначала
введем параметр толерантности ,
устанавливающий степень генерализации карты, зависимый от масштаба и выбираемый
эмпирически. Пусть Vi – начальная точка, а Vj
– конченая точка полилинии. Вычислим расстояния от всех остальных точек полилинии
до прямой Vi ,Vj , найдем из них максимальное
dmax и обозначим наиболее удаленную от Vi ,Vj
точку Vf . Если dmax < , то все точки между Vi
и Vj удаляются, а Vi ,Vj представляет генерализированную
линию. Если dmax
, то полилиния
Vi ,Vj расщепляется на две
Сначала
введем параметр толерантности ,
устанавливающий степень генерализации карты, зависимый от масштаба и выбираемый
эмпирически. Пусть Vi – начальная точка, а Vj
– конченая точка полилинии. Вычислим расстояния от всех остальных точек полилинии
до прямой Vi ,Vj , найдем из них максимальное
dmax и обозначим наиболее удаленную от Vi ,Vj
точку Vf . Если dmax < , то все точки между Vi
и Vj удаляются, а Vi ,Vj представляет генерализированную
линию. Если dmax
, то полилиния
Vi ,Vj расщепляется на две
![]()
части – Vi ,Vf и Vf ,Vj , для которых рекурсивно
выполняется данный алгоритм.
Тема 5. Привязка геоданных к карте и преобразования координат
Картографическое отображение действительности заключается в пространственном, математически определенном и генерализованном представлении информации об окружающем мире в знаковой форме карты. Привязка географических данных к математической координатной основе (проекции) в ГИС выполняется чаще всего по топографическим картам и реперным точкам.
Математическая основа карты определяет взаимосвязь между картой и отображаемой поверхностью и включает в себя картографическую проекцию, систему координат, масштаб. В картографии используются геодезические координаты эллипсоида – широта и долгота и прямоугольные координаты на плоскости карты, изображенной в какой-либо проекции. Основной задачей математической картографии является построение проекций – способов изображения объектов, расположенных на поверхности земного эллипсоида, на плоскости. Общее уравнение картографических проекций связывает геодезические и плоские прямоугольные координаты и записывается в виде x f1(,); y f2(,) , где и - географические координаты точки на географической поверхности, x и y - прямоугольные координаты на плоскости карты.
Выбор картографической проекции определяется географическим положением картографируемого объекта, особенностями создаваемой карты и требованиями к характеру и величине искажений. Картографическая проекция выбирается таким образом, чтобы ее центральные точки находились в центре картографируемой области, а центральные линии располагались по направлению наибольшей протяженности объекта.
В нашей стране основной проекцией для создания традиционных и цифровых топографических карт является проекция Гаусса – Крюгера. Проекция Гаусса-Крюгера – равноугольная, симметричная относительно осевого меридиана и экватора. Осевой меридиан в этой проекции изображается прямой, вдоль которой длины отображаются без искажений.
В проекции Гаусса вся поверхность Земли условно разделена на 60 зон меридианами, проведенными через 6°; форма зоны – сферический двуугольник (рисунок 5.1); счет зон ведется от Гринвичского меридиана на восток. Средний меридиан зоны называется осевым; долгота осевого меридиана L0 любой зоны в восточном полушарии подсчитывается по формуле: L0=6°*n – 3°, (5.1) где n – номер зоны.
Представим себе земной эллипсоид, вписанный в эллиптический цилиндр. Ось цилиндра расположена в плоскости экватора и проходит через центр эллипсоида (рисунок 5.1). Цилиндр касается эллипсоида по осевому меридиану данной зоны. Вся поверхность зоны проектируется на поверхность цилиндра нормалями к эллипсоиду так, что изображение малого участка на цилиндре подобно соответствующему участку на эллипсоиде. Такая проекция называется конформной или равноугольной; в ней углы не искажаются, а длины линий искажаются по закону:
S Y 2
![]() 2 , (5.2)
2 , (5.2)
S 2 R
где: ΔS – величина искажения линии,
S – длина линии на эллипсоиде,
Y – удаление линии от осевого меридиана,
R – средний по линии радиус кривизны эллипсоида.

Для территории нашей страны искажения длин линий находятся в допустимых пределах для карт масштабов 1/10000 и мельче; для карт масштаба 1/5000 и крупнее приходится применять трехградусные зоны Гаусса. Поверхность цилиндра разрезается и развертывается на плоскости; при этом осевой меридиан и экватор изображаются в виде двух взаимно перпендикулярных прямых линий. В точку их пересечения помещают начало прямоугольных координат зоны. За ось OX принимают изображение осевого меридиана зоны (положительное направление оси OX – на север), за ось OY принимают изображение экватора (положительное направление оси OY – на восток). При координате Y впереди пишут номер зоны; для исключения ее отрицательных значений условились, что в начале координат значение координаты Y равно 500 км.
Общее уравнение равноугольных проекций может быть записано в виде x iy F(q i) где q и – изометрические координаты. Функция F может быть получена различными способами; в проекции Гаусса используется разложение в ряд Тейлора:
dF(q) (i)2 d2F(q) (i)3 d3F(q)
![]() F(q i) F(q) i 2 3 L , (5.3)
dq 2! dq 3! dq
F(q i) F(q) i 2 3 L , (5.3)
dq 2! dq 3! dq
откуда, приравняв действительные и мнимые части, получим
![]()
![]() 2 d2F(2q) 4 d4F(4q) ; ydF(q) 3 d3F(3q) 5 d5F(5q)L . (5.4) xF(q) L
2 d2F(2q) 4 d4F(4q) ; ydF(q) 3 d3F(3q) 5 d5F(5q)L . (5.4) xF(q) L
2 dq 24 dq dq 6 dq 120 dq
Из условия отображения без искажений вдоль линии осевого меридиана следует, что F(q) sm , где sm – расстояние от экватора до текущей параллели. Для эллипсоида Красовского
sm 6367558,516036,5sin216,8sin4.
2 d 2 s 4 d 4 s
![]() x s m
2m
4m
L
; (5.5) 2 dq 24 dq
x s m
2m
4m
L
; (5.5) 2 dq 24 dq
![]() ds 3 d 3 s 5 d 5 s y
m
3m
5m L .
ds 3 d 3 s 5 d 5 s y
m
3m
5m L .
dq 6 dq 120 dq
Запишем первые производные sm :
![]() dsm r N cos
;
dsm r N cos
; ![]() d4s4m N cos3sin5t2 92 44 ; dq dq
d4s4m N cos3sin5t2 92 44 ; dq dq
![]()
![]() d2sm
; d5s5m
N cos5518t2 t4 142 582t2
;
d2sm
; d5s5m
N cos5518t2 t4 142 582t2
;
r sin N cossin
dq2 dq
![]()
![]() d3sm 3
MN cossin22
N cos31t2 2
;
N cos dq3
d3sm 3
MN cossin22
N cos31t2 2
;
N cos dq3
sin2 где
t2 ![]() 2 ,
e2 cos2, cos
2 ,
e2 cos2, cos
a
N - радиус кривизны сечения первого вертикала,
![]() 1e2 sin2 e2 - квадрат первого эксцентриситета
эллипсоида, e2 - квадрат второго эксцентриситета
эллипсоида.
1e2 sin2 e2 - квадрат первого эксцентриситета
эллипсоида, e2 - квадрат второго эксцентриситета
эллипсоида.
Подставим найденные производные в уравнения (5.3) и получим уравнения проекции Гаусса:
2 4
3 2 2 4
x sm ![]() N sincos
N sincos ![]() N sincos (5t 9
4
)K; (5.6)
N sincos (5t 9
4
)K; (5.6)
2 24
3 3 2 2 5 5 2 4 2 2 2
y
N cos B ![]() N cos (1t
)
N cos (1t
) ![]() N cos (5 18t
t 14 58 t ) .
N cos (5 18t
t 14 58 t ) .
6 120
Координатами Гаусса-Крюгера точки земного эллипсоида называются плоские прямоугольные координаты изображения этой точки в проекции Гаусса-Крюгера. Поверхность земного эллипсоида делится меридианами на шестиградусные зоны. Часть поверхности эллипсоида, соответствующая некоторой зоне, проецируется на плоскость, на которой задана прямоугольная система координат с началом в точке пересечения осевого меридиана зоны с экватором (рисунок 5.2-а). В системе координат Гаусса-Крюгера в каждой зоне используется собственная система координат.
Координатой X в этой системе координат является расстояние точки от экватора, координатой Y – расстояние от осевого меридиана (рисунок 5.2-
б). Чтобы исключить отрицательные значения координат, к координате Y прибавляют 500000 м. Для описания принадлежности точки к зоне, к координате Y слева приписывается номер зоны.

P2
а) б)
Рисунок 5.2 – Система координат Гаусса–Крюгера 1942г.:
а) – изображение зоны; б) – совмещение координат на границе зон
Одной из важнейших функций ГИС для обработки пространственных данных является преобразования координат картографических проекций. Эти операции чаще всего встречаются при вводе пространственных данных, визуализации, а также при трансформации карт из одной проекции в другую.
Во время оцифровки бумажных карт дигитайзером векторное изображение создается в системе координат дигитайзера. При этом получившийся слой “наследует” проекцию, в которой выполнен исходный картографический материал. Для пространственной привязки оцифрованных материалов следует преобразовать данные в систему координат проекции исходной карты. Для этого достаточно операций сдвига, поворота и масштабирования. Коэффициенты линейного преобразования определяются по опорным точкам.
Рассмотрим группу операций аффинного преобразования. В неё входят масштабирование, поворот изображения и перенос начала координат. В общем случае эти операции сводятся к преобразованию прямоугольных координат точек объектов карты при помощи матрицы P :
|
X x 1 Y P y, P AAA 0 1 1 0 |
0 1 0 |
xx y 0 1 0 |
0 y 0 |
0 cos 0sin 1 0 |
sin cos 0 |
0 0 , (5.7) 1 |
где x и y – исходные координаты точки, X и Y – новые координаты, x,y – смещения начала координат, x ,y – коэффициенты изменения масштаба по осям, – угол поворота осей новой системы координат относительно старой. Матрица A отвечает за перенос начала координат, матрица
A - за изменение масштабов по осям x и y , а матрица A- за поворот изображения. Аффинное преобразование выражается линейными уравнениями
X a0 a1x a2y; Y b0 b1x b2y.
Часто возникает задача трансформации координат при неизвестных значениях x,y , x ,y , . В этом случае для получения уравнения преобразования используются опорные точки, для которых известны координаты (xi , yi )i1Ln в исходной системе координат и (X i ,Yi )i1Kn в новой системе. Будем искать функцию преобразования системы координат (X,Y) F(x, y) , X Fx (x, y), Y Fy (x, y) при помощи метода наименьших квадратов в виде
m m
X Fx (x, y) a j f j (x, y) , Y Fy (x, y) bj f j (x, y), где fi (x, y) - множество ба-
j0 j0
зисных функций. Вычислим коэффициенты a j . Будем искать минимум
n m 2
функции Ex X i ( a j f j (xi , yi )) min. Для этого приравниваются к нулю
i1 j1
частные производные от Ex по коэффициентам a j . Необходимые условия минимума образуют систему уравнений
E n m
![]() 2 (X i a j f j (xi , yi )) f1(xi , yi
)
0
2 (X i a j f j (xi , yi )) f1(xi , yi
)
0
a1 i1 j1
M , (5.8)
n m
![]() E i1 2 (Xi j1a j f j (xi , yi ))
fm (xi ,
yi ) 0
E i1 2 (Xi j1a j f j (xi , yi ))
fm (xi ,
yi ) 0
am
которая после тождественных преобразований приобретает вид
m n n
a j f1(xi , yi ) f j (xi , yi ) X i f1(xi , yi )
j1 i1 i1
M . (5.9)
m n n
a j fm (xi , yi ) f j (xi , yi ) X i fm (xi , yi )
j1 i1 i1
В матричном выражении условия минимума запишутся как
(f1, f1) (f1, f2) L (f1, fm)a1 (f1,X)
(f2, f1) (f2, f1) L (f2, fm)a2 (f2,X)
M M O M M M , (5.10)
(fm, f1) (fm, f2) L (fm, fm)am (fm,X)
где ( f j , fk ) f j (xi , yi ) fk (xi , yi ), ( f j ,X) f j (xi , yi ) X i .
i i
Необходимая точность преобразования достигается расширением количества базисных функций. Если после нахождения аппроксимирующей
n m 2
функции на некотором базисе невязка Ex X i ( a j f j (xi , yi )) превышает
i1 j1
требуемую точность, то нужно добавить в набор базисных функций новые функции. Приближение для функции Fy (x, y) находится аналогично.
Более сложные преобразования координат становятся необходимы, когда цифровая карта трансформируется из одной картографической проекции в другую. Для выполнения таких операции уже недостаточно линейных преобразований. Здесь используются уравнения проекций, итерационные методы, и аппроксимация функции преобразования по опорным точкам.
Выделим три вида преобразований картографических проекций. Преобразования геодезических координат в координаты некоторой проекции выполняются непосредственно по уравнениям проекции. В программном обеспечении большинства современных ГИС имеются встроенные средства для вычисления координат наиболее распространенных проекций. Поэтому целесообразно хранить координаты объектов в географической системе координат и при необходимости преобразовывать карту в нужную проекцию. Для преобразования координат проекций в ГИС-приложениях можно использовать также Си-библиотеку PROJ4.
Второй вид преобразований картографических проекций соответствует обратной задаче: по известным плоским прямоугольным координатам требуется получить геодезические координаты. Исторически основной задачей математической картографии являлось изображение на плоскости карты объектов, расположенных на поверхности эллипсоида. Поэтому проекции выражаются в виде уравнений, связывающих геодезические координаты точки (широту и долготу) с плоскими прямоугольными координатами. Следует отметить, что непосредственное получение из уравнений проекции нужных преобразований затруднительно. Вместо этого используется принцип сжимающих отображений. По уравнениям картографической проекции
f3(,,x, y)
x f1(,); y f2(,) составим систему уравнений вида: .
f4(,,x, y) Если функции f3 и f4 определены, действительны и непрерывны в окрестности решения *,*, система может быть решена методом итераций:
n1 f3(n ,,x, y)
. (5.11)
n1 f4(n ,,x, y)
Например, для проекции Гаусса–Крюгера по уравнениям проекции можно построить быстро сходящийся (рисунок 5.3) итерационный процесс нахождения геодезических координат по координатам проекции.
![]() n1 x16036,5sin2n 16,8sin4n
n1 x16036,5sin2n 16,8sin4n ![]() 2 N sinn cosn
2 N sinn cosn ![]() 4 N sinn cos3n K;
(5.12)
4 N sinn cos3n K;
(5.12)
2 24
![]()
![]() n1 1
n3 3 n5 5
. (5.13)
n1 1
n3 3 n5 5
. (5.13)
y N cos N cos
N cosB 6 120
В качестве начального приближения 0,0 можно принять значения, найденные при помощи аппроксимации функций f3 и f4 полиномами невысокого порядка по опорным точкам.
|
|
|
Рисунок 5.3 – Сходимость итерационного процесса нахождения географических координат по координатам Гаусса-Крюгера
Если имеется цифровая карта в некоторой заданной проекции, можно преобразовать ее в другую проекцию, преобразовав ее в географическую систему координат и воспользовавшись уравнениями требуемой проекции.
Третий вид преобразований картографических проекций включает преобразования координат между двумя проекциями, когда проекция исходной карты неизвестна. Если имеется достаточное количество опорных точек, для которых известны координаты (xi , yi )i1Ln и (X i ,Yi )i1Kn в обеих проекциях, то можно найти функции, аппроксимирующие f3(x, y) и f4(x, y). Чаще
n n всего их ищут в виде алгебраических степенных полиномов вида aijij .
i 0 j 0
На выбор аппроксимирующих функций оказывают влияние вид картографической сетки, характер искажений проекций. Оценивать точность преобразования можно по невязке в контрольных точках, для которых известны координаты в обеих проекциях и которые не используются в качестве опорных.
Способы построения аппроксимирующих зависимостей позволяют обеспечить необходимую точность только для локального преобразования, но не дают возможностей для трансформирования в пределах всей области. Однако для трансформации небольших участков карты или при отсутствии уравнений исходной проекции этот метод может оказаться более удобным.
Нелинейные преобразования координат необходимы и при регистрации космических снимков. Здесь также определяются опорные точки, по которым находится уравнение, связывающее системы координат растрового изображения и векторного слоя.

Рисунок 5.4 – Географическая привязка изображения в ГИС MapInfo
Существует два подхода к использованию растровых изображений в векторных ГИС. Первый из них подразумевает трансформацию растрового слоя под проекцию цифровой карты. Преобразованный снимок совмещается с цифровой картой линейным преобразованием, что позволяет совместно визуализировать их непосредственно во время работы. Второй подход основан на привязке векторного изображения к растровому слою. Векторная модель хотя и имеет более сложную структуру, чем растровая, но обычно содержит на порядок меньшие объемы пространственных данных. Поэтому возможно совместное отображение растровых и векторных слоев с нелинейными преобразованиями координат векторов непосредственно во время просмотра.
На рисунке 5.4 показан процесс привязки растровой карты
в ГИС MapInfo. В качестве опорных точек используются пересечения линий координатной
сети. Координаты точек определяются по подписям километровой сети в зарамочном оформлении
карты.
Тема 6. Векторизация картографического изображения
Цифровые карты, схемы и планы являются одним из основных источников данных в ГИС-проектах. Объекты, изображаемые на картах, чаще всего представляются в математических моделях графами, а в ГИС – векторной моделью данных. Векторизация — перевода растрового изображения в векторное, процесс обратный растеризации. В отличие от растеризации, этот процесс очень сложен и не может быть выполнен полностью автоматически.
Процесс ввода карт в ГИС весьма трудоемок. Итоговая цифровая карта содержит десятки тысяч объектов, каждый из которых может состоять из нескольких сотен сегментов. Так при ручной векторизации даже средней по размерам карты оператор вводит сотни тысяч и даже миллионы точек.
В настоящее время используется две основных технологии векторизации карт: векторизация исходного бумажного материала при помощи электромеханических дигитайзеров и векторизация сканированного изображения карты программным путем. Дигитайзерная технология векторизации карт автоматизации не поддается, поэтому все попытки уменьшения трудоемкости процесса векторизации основаны на «сканерной» технологии и автоматизации операций выделения векторных объектов на растровом слое. Подходы к векторизации сканированной карты можно разделить на три группы.
При ручной векторизации оператор обводит линии и контуры картографических объектов по растровой подложке (по трудоемкости этот способ эквивалентен дигитайзерной векторизации и позволяет векторизовать в среднем 1-2 объекта в минуту). При полуавтоматической (интерактивной) векторизации используется программы, в которых оператор устанавливает стартовую точку линейного сегмента, и далее программа автоматически трассирует линию до её окончания или разветвления. Дальнейшее направление трассировки программа получает из диалога с оператором.
При автоматической векторизации программа автоматически преобразуют в векторы все объекты растровой карты заданного класса, оставляя оператору лишь окончательное редактирование и коррекцию ошибок в полученном векторном слое. Однако на практике из-за низкого качества исходных материалов автоматические векторизаторы часто выдают высокий процент ошибок, необходимость ручного исправления которых снижает эффект от автоматизации процесса векторизации.
Технологическая схема векторизации по «сканерной» технологии (рисунок 6.1) начинается со сканирования и геопривязки исходного материала, разработки структуры ГИС-проекта (декомпозиции карты, определения состава слоев и таблиц и т.д.). Для наиболее полного использования возможностей автоматической векторизации проводится предварительная обработка растрового поля, а для распараллеливания работы между операторами – сегментация проекта. Сегментация проекта может проводиться как по слоям, когда каждый оператор векторизует отдельный тематический слой, так и по территории. После того, как карта тем или иным способом векторизована и верифицирована, проводится сшивка сегментов и данные поступают в ГИС.

Рисунок 6.1 – Схема векторизации картографического изображения
Основное назначение предобработки отсканированной карты – преобразовать растровое картографическое изображение так, чтобы улучшить его распознаваемость картографических объектов в автоматических векторизаторах. На исходных бумажных картах часто присутствуют пятна, потертости, типографский брак и другие дефекты, затрудняющие автоматическое распознавание объектов и преобразование их в векторы. Для улучшения изображений используют алгоритмы локальной фильтрации, улучшения гистограмм и др.
Разбиение отсканированной карты на слои осуществляется тематическим цветоделением – выделением на изображении смысловых классов по цвету. При печати карт в типографии используется ограниченное количество цветов. Так, на топографических картах используются оттенки 6 цветов: черного, синего, голубого, коричневого, зеленого, малинового. Оператор при помощи инструмента “пипетка”, имеющегося во всех современных пакетах обработки растровых изображений, выделяет основной цвет тематического слоя – (R0, G0, B0) и вводит величину разброса Δ. Этим в пространстве палитры RGB задается параллелограмм (рисунок 6.2). Если цвет пикселя растрового изображения попадает внутрь этого параллелограмма, то пиксель включается в выборку.

Рисунок 6.2 – Тематическое цветоделение. Параллелепипед RGB
Выделение линейных и площадных объектов на растровом изображении выполняется при помощи алгоритмов выделения границ, большая часть которых основана на предположении, что граница проходит там, где имеются разрывы в функции интенсивности I или крутой градиент. Используя это предположение, вычисляют значения магнитуды градиента интенсивности изображения и находят точки, где она максимальна. Эти точки образуют границы (рисунок 6.3). На дискретных растровых изображениях градиент можно вычислить, просто взяв разность значений интенсивности соседних пикселей (рисунок 6.3-б), что эквивалентно свертке изображения с маской [-1,1].
![]() I I Градиент
изображения (функции I ) задается вектором I
x , y
.
I I Градиент
изображения (функции I ) задается вектором I
x , y
.
 x
.
x
.
Рисунок 6.3 – Профиль границы на изображении и его производная
Для вычисления градиента можно использовать любую пару ортогональных направлений, хотя обычно используются направления вдоль линии столбцов и строк растрового изображения (оси oX и oY). В простейшем градиентном операторе (Robert's Cross operator) используются диагональные
0 1 1 0 направления, которому соответствуют маски и .
1 0 0 1
Рассмотрим способы преобразования бинарных изображений, основанные на операторах математической морфологии – аппарата для исследования структуры множеств однотипных объектов (от греч. μορφή «форма» и греч. λογία). В бинарном изображении – упорядоченном множестве черно-былых пикселей – под объектом изображения обычно понимается некоторое подмножество пикселей изображения со значениями 0 или 1 (если фон – черный, то объекты – белые; если фон – белый, то объекты – черные).
Операции бинарной математической морфологии являются некоторым преобразованием этого множества, в котором в качестве исходных данных принимается бинарное изображение B и структурный элемент S, комбинируют их используя множественные операции , , и др., а результатом является бинарное изображение N.

Рисунок 6.4 – Примеры формы структурных элементов
Морфологические операции преобразуют объекты входного изображения на основе характеристик их формы. Эти характеристики задаются в структурном элементе – двоичном изображении произвольного размера и формы. Чаше всего используются симметричные элементы: прямоугольник фиксированного размере BOX(l,w), круг некоторого диаметра DISK (d) (рисунок 1). В каждом элементе выделяется особая точка, называемая начальной (origin). При выполнении операции каждый пиксель исходного изображения со своей окрестностью сопоставляются со структурным элементом. При этом место начальной точки структурного элемента должно совпадать с положением обрабатываемого в текущий момент пикселя изображения. Если эти два множества удовлетворяют условиям, заданным множественным оператором, значение пикселя в выходном слое устанавливается в “1”, иначе – в “0”.
В математической морфологии есть две базисные операции – расширение (dilation) и сужение (erosion). Производные операции – это некоторая комбинация базисных, выполняемых последовательно. Основными из производных операций являются открытие (opening) и закрытие (closing).
Перенос (translation) множества пикселей X на вектор t определяется как X t {x t | x X}. Перенос t может быть определен как упорядоченная пара чисел (x,y) , где x - движение вдоль оси х, а y - движение вдоль оси y.
Расширение двоичного изображения B на структурный элемент S записывается в виде B S и определяется как B S USb . Если при обходе рас-
bB
тра начальная точка структурного элемента накладывается на 1, то весь структурный элемент записывается в результирующее изображение. Таким образом, при выполнении расширение размеры изображения увеличиваются.
Сужение двоичного изображения B на структурный элемент S записывается в виде B S и определяется как BS {b | bsBsS}. Проверяется, что каждая 1 в структурном элементе накладывается на 1 в исходном изображении. Если это условие выполнено, то в результирующее изображение записывается пиксель под начальной точкой структурного элемента.
Закрытие двоичного B на структурный элемент S записывается B S и определяется как B S (B S) S . Операция закрытия «закрывает» небольшие внутренние «дырки» в изображении, и убирает углубления (bays) по краям области. Открытие двоичного B на структурный элемент S записывается как BoS и определяется как B o S (B S) S . Открытие позволяет избавиться от небольших кусочков изображения, выходящих за границу области. Над парой двоичных изображений также могут применяться обычные теоретико-множественные логические операции как AND, OR, NOT, MINUS.

Структурный элемент S
Рисунок 6.5 – Примеры выполнения морфологических операций
Для поиска на бинарном изображении особых шаблонов из 1 и 0 применяется преобразование Hit&Miss. В этом преобразовании в отличие от предыдущих морфологических операторов структурный элемент может содержать не только 1, но и 0 (рисунок 6.6).
Преобразование Hit&Miss выполняется почти также, как другие морфологические операторы – трансляцией структурного элемента на все пиксели изображения. Если значения клеток структурного элемента (нули и единицы на рисунке 1-А) лежат точно совпадают со значениями пикселей лежащего под структурным элементом изображения, то значение пикселя под начальной точкой структурного элемента устанавливается в «1», в противном случае – в «0».
Структурный элемент на рисунке 6.6-а позволяет находить левые нижние углы объекта. Чтобы на бинарном изображении найти все углы, нужно четыре раза выполнить Hit&Miss-преобразование с этим структурным элементом, каждый раз поворачивая шаблон на 90, и сложить четыре получившихся бинарных изображения функцией OR (рисунок 6.6-б).
На рисунке 1-В показан структурный элемент, использующийся для поиска изолированных точек (шум перец – pepper-noise), на рисунке 1-Г – шаблон для обнаружения оконечных точек бинарного скелетона (нужно выполнить 4 сравнения, каждый раз поворачивая шаблон на 90). Для поиска ветвлений границы используются шаблоны на рисунке 1-Д (шаблон также в 4 позициях).

|
|
|
|
в) г) д)
Рисунок 6.6 – Схема выполнения и примеры Hit&Miss-преобразований
Преобразование Hit&Miss могут использоваться для утоньшения линий (скелетонизация). На рисунках 6.8-а и 6.8-б приведены структурные элементы для этой операции. Для выделения 4-связных и 8-связных границ используются шаблоны на рисунках 6.8-в и 6.8-г. Границы объектов на бинаризованом изображении часто содержат «шпоры», удалить которые можно итеративным выполнением операции спрямления (pruning), рисунок 6.8-д и 6.8-е.

Рисунок 6.7 – Эффект применения Hit&Miss-оператора (рисунок 6.6-б)
Утоньшение Поиск границ Прунинг
|
0 |
0 |
0 |
|
|
0 |
0 |
|
1 |
1 |
1 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|||||
|
1 |
1 |
1 |
|
1 |
|
1 |
1 |
1
|
0 |
1 |
0 |
0 |
|
|
|
|
0 |
а) б) в) г) д) е)
Рисунок 6.8 – Hit&Miss-преобразования для работы с границами
Утоньшенное изображение преобразуется в векторную структуру, сохраняющую топологию объектов исходной отсканированной карты, т.е. в графы. Методы получения векторного представления можно разделить на отслеживающие, сканирующие и их комбинации. Алгоритмы растрововекторных преобразований работают в основном с бинарными изображениями и основаны на сборке связных пикселов растра в цепочки пикселов с последующим преобразованием их центроидов в узлы полилиний и полигонов. Для определения связности пикселов используют соседство по 8 направлениям (ход королевы, рисунок 6.9-а) или по 4 направлениям (ход ладьи, рисунок 6.9-б). Будем считать, что значение пикселя «1» означает присутствие объекта, а «0» – его отсутствие. Валентность пикселя со значением «1» называется число соседних пикселей со значением «1». Легко видеть, что начало и конец цепочки пикселей (будущей полилинии или полигона) имеют валентность 1, внутренние точки цепочки пикселей – валентность 2, а места разветвлений – валентность 3 (рисунок 6.9-д).

а) б) в) г) д) Точка А
Рисунок 6.9 – Выделение цепочки пикселей
Используя эти свойства, нетрудно построить алгоритмы выделения на растровом изображении изолированных связных цепочек пикселей и превратить эти цепочки в полилинии и полигоны. Предложим один из таких способов автоматического растрово-векторного преобразования.
Выполним перебор всех пикселей растра со значением «1» и будем заносить их в структуру данных, показанную на рисунке 6.10. Здесь цепочки представлены однонаправленными списками пикселей, а сам список цепочек – списком списков пикселей. Если первый или последний пиксель в списке любой из цепочек 1..k соседствуют с добавляемым пикселем, текущий пиксель помещается соответственно в начало или в конец этой цепочки.
Если текущий пиксель не попал ни в одну из существующих цепочек, создается новая цепочка и в нее заносится текущий пиксель. Если валентность добавляемого в существующую цепочку пикселя не равна 2, то достигнут конец линии или ее ответвление, и с этого конца цепочки пиксели дальше не добавляются.

Рисунок 6.10 – Структура данных для глобального растрово-векторного преобразования
В полуавтоматическом режиме оператор указывает «затравочную точку» – пиксель со значением «1» и далее алгоритм векторизации трассирует цепочку, рекурсивно перемещаясь к соседнему пикселю, пока не будет достигнут конец цепочки или её ответвление (т.е. пиксель с валентностью, не равной 2).
Известны алгоритмы векторизации утоньшенного растра, использующие для векторизации линий метод цепного кодирования с помощью кодов Фримана. Пиксели скелета предварительно кодируются следующим образом: 0 – пиксель фона, 1 – конечный пиксель линии, 2 – промежуточный пиксель, 3 – узловой пиксель. Линии трассируются, начиная с пикселей 1 и 3, и сохраняются в виде цепочек Фримана. Такой метод векторизации обеспечивает высокую степень сжатия изображения при сохранении топологии исходного изображения.
Преобразование Хоха позволяет находить на монохромном изображении заданные параметрически плоские кривые (прямые, окружности, и др.), образованные пикселями со значением «1». Идея преобразования Хафа состоит в поиске кривых, которые проходят через достаточное количество точек интереса.
Рассмотрим семейство кривых на плоскости, заданное параметрическим уравнением: F(a1, a2, …, an, x, y) = 0; где F – некоторая функция, a1, a2, …, an – параметры семейства кривых, x, y – координаты на плоскости. Параметры семейства кривых образуют фазовое пространство, каждая точка которого (конкретные значения параметров a1, a2, …, an) соответствует некоторой кривой. Ввиду дискретности машинного представления и входных данных (изображения), требуется перевести непрерывное фазовое пространство в дискретное. Для этого в фазовом пространстве вводится сетка, разбивающая его на ячейки, каждая из которых соответствует набору кривых с близкими значениями параметров. Каждой ячейке фазового пространства можно поставить в соответствие число (счетчик), указывающее количество точек интереса на изображении, принадлежащих хотя бы одной из кривых, соответствующих данной ячейке. Анализ счетчиков ячеек позволяет найти на изображении кривые, на которых лежит наибольшее количество точек интереса.
Прямую на плоскости можно задать уравнением: x cosθ + y sinθ = R, где R – длина перпендикуляра опущенного на прямую из начала координат, θ - угол между перпендикуляром к прямой и осью OX (рисунок 6.11), θ изменяется в пределах от 0 до 2π, а R – ограничено размерами входного изображения. Таким образом, функция, задающая семейство прямых, имеет вид: F (R, θ, x, y) = x cosθ + y sinθ - R.

а) б) в)
Рисунок 6.11 – Параметрическое представление прямой
Через каждую точку (x, y) изображения можно провести несколько прямых с разными R и θ (рисунок 6.11-б), то есть каждой точке (x, y) изображения соответствует набор точек в фазовом пространстве (R, θ), образующий синусоиду (рисунок 6.11-в). Каждой точке пространства (R, θ) соответствует набор точек (x, y) на изображении, образующий прямую. Каждой точке (R0, θ0) пространства (R, θ) можно поставить в соответствие счетчик, соответствующий количеству точек (x, y), лежащих на прямой x cosθ0 + y sinθ0 = R0.
Ввиду дискретности машинного представления и входных данных, требуется перевести непрерывное фазовое пространство в дискретное. Введем сетку на пространстве (R, θ), одной ячейке которой соответствует набор прямых с близкими значениями R и θ. Теперь счетчик ставится в соответствие каждой ячейке сетки: ячейке [Ri, Ri+1] x [θi,θi+1] соответствует число точек, удовлетворяющих уравнению x cosθ + y sinθ = R, где θi ≤ θ ≤ θi+1, Ri ≤ R ≤ Ri+1.
Размер ячеек стоит выбирать, учитывая следующие соображения. Если ячейки будут очень большими, то за "прямую" может приниматься разрозненный набор точек. Если же ячейки будут слишком малы, возможно не найдется ни одной прямой – все счетчики будут иметь небольшое значение. Алгоритм преобразования Хоха выглядит так: обнулить счетчики всех ячеек; для каждой точки интереса:
для каждой прямой, проходящей через данную точку:
- увеличить соответствующий счетчик;
- выбрать ячейку с максимальным значением счетчика;
- параметры прямой, проходящей через максимальное число точек принять равным координатам центра выбранной ячейки в фазовом пространстве;
Если прямых нужно найти несколько, можно отсортировать счетчики по убыванию или рассматривать точки локальных максимумов фазового пространства. На рисунке 6.12 изображены примеры исходных изображений и соответствующих им фазовых пространств. Следует отметить, что преобразование Хоха мало чувствительно к шуму и пробелам.

Рисунок 6.12 – Пример работы преобразования Хоха. Величина счетчика в каждой точке фазового пространства показана яркостью
Геометрическое место точек окружности можно представить в виде формулы: (x – a)2 + (y – b)2 = R2, где (a, b) – координаты центра окружности, а R – ее радиус. Т.е. формула, задающая семейство окружностей, имеет вид:
F (a, b, R, x, y) = (x – a)2 + (y – b)2 – R2.
Если ставится задача найти окружность заранее известного радиуса, фазовым пространством будет плоскость параметров центра окружности (a, b). В таком случае, алгоритм выделения окружностей полностью аналогичен алгоритму нахождения прямых. Если радиус окружности заранее неизвестен, то пространство параметров будет трехмерным – (a, b, R), что существенно увеличивает вычислительную сложность решения задачи.
Следует помнить, что эффективность использования преобразования Хафа резко падает при увеличении размерности фазового пространства, поэтому перед его применением желательно минимизировать каким-либо образом количество параметров кривой. Вообще, преобразование Хафа можно применить не только для выделения плоской параметрической кривой, но и любой фигуры, форма которой полностью определяется некоторым набором параметров, например прямоугольника, треугольника, и т.д.

Рисунок 6.13 – Иллюстрация работы преобразования Хоха
На рис. 6.13-а приведено исходное изображение– два пересекающихся прямоугольника. Градиентный фильтр выделяет линии границы этой фигуры. На рисунке 6.13-б видны все границы фигуры, но результат не говорит об опознанности объекта (и качестве распознавания). Применим преобразование Хоха (детектор линий) чтобы выделить восемь отдельных прямых сегментов границы и идентифицировать настоящую геометрическую структуру объекта. Полученные прямые в пространстве (R, θ) в виде массива счетчиков изображены на рис. 6.13-в. Улучшив контрастность изображения, видим пиксели с высокой интенсивностью, отражающие структуру объекта (рисунок 6.13-г).
Заметим, что (R, θ) – полярные координаты, а «пространство счетчиков» изображено в виде прямоугольной матрицы. Это пространство «заворачивается» на вертикальной границе изображения, поэтому на самом деле имеем только 8 реальных пиков. Прямые линейные сегменты на градиентном изображении (рисунок 6.13-б) пересекаются в пиках в пространстве (R, θ). Существуют несколько способов выделения этих ярких точек (локальных максимумов) из массива 6.13-в. Например, можно использовать пороговую фильтрацию с последующим применением Thining-алгоритма к изолированным кластерам.
Обратное преобразование из пространства (R, θ) в декартову
систему координат порождает множество описаний линий сегмента границы. Оверлей результата
и инвертированного исходного изображения показан на рисунке 6.13-д. Точность выравнивания
оригинального изображения и результата неидеальна из-за квантования аккумулирующей
матрицы, а полученные прямые имеют
длину.
Тема 7. Глобальные системы позиционирования
Последним крупным достижением в области геодезии является автономное определение координат точек, расположенных на и вблизи земной поверхности. Слово "автономный" означает, что при производстве наблюдений на определяемом пункте не требуется прямой видимости на соседние пункты. Спутниковые навигационные системы используются в ГИС для геодезического обеспечения картографирования территории страны и акваторий окружающих ее морей, геодезического обеспечения проведения земельной реформы, ведения кадастров, строительства, добычи и разведки природных ресурсов, определение местоположения транспортных средств на суше, на воде и в воздухе.
Автономное определение координат выполняется с помощью спутниковых навигационных систем – 1-го поколения ЦИКАДА (Россия) и TRANSIT (США) и 2-го поколения ГЛОНАСС (Россия) и NAVSTAR (США). Система NAVSTAR также имеет название Global Positioning System (GPS). Cпутники NAVSTAR вращаются вокруг Земли по круговым орбитам на высоте около 20000 км, наклон орбиты – 55. Наземный командноизмерительный комплекс этой системы включает координационновычислительный центр, командно-измерительную станцию, станции слежения и станции закладки служебной информации (рисунок 7.1). При использовании российских навигационных систем координаты определяемых пунктов получаются в системе координат 1942 года (СНС ЦИКАДА) или в системе СГС-90 (СНС ГЛОНАСС), при использовании американских – в системе координат WGS-84.

Рисунок 7.1 – Сеть контрольных станций GPS
Используются абсолютный и относительный режимы определения координат с помощью СНС. При абсолютном способе получают координаты антенны в принятой системе координат; при относительном способе комплект аппаратуры распределяется на два пункта, один из которых имеет известные координаты, и из наблюдений определяют приращения координат между этими пунктами. Точность получаемых величин зависит от способа определения координат, от типа аппаратуры и от кода сигналов спутника и варьируется от десятков метров до миллиметров.
В спутниковых навигационных системах 1-го поколения для определения местоположения использовался эффект сдвига частот радиоизлучения движущегося источника (эффект Доплера). Одно наблюдение спутника позволяет написать уравнение одной линии положения, имеющей форму либо гиперболы (доплеровский дифференциальный метод) либо более сложной кривой изодопы (доплеровский интегральный метод). При n наблюдениях положение наблюдателя получается в одной из точек пересечения n соответствующих гипербол или изодоп.
В спутниковых навигационных системах 2-го поколения измеряются "дальности" – расстояния от определяемой точки до спутников, координаты которых известны на любой момент времени. Геометрическая идея такого определения заключается в нахождении положения точки из трехмерной линейной засечки; положение точки фиксируется либо тремя прямоугольными координатами X, Y, Z либо геодезическими координатами на эллипсоиде (широтой B и долготой L) и высотой H над поверхностью эллипсоида.
При обработке наблюдений спутников приходится учитывать параметр "время", поэтому для однозначного решения засечки требуется наблюдать 4 спутника, расположенных равномерно по азимуту (через 90°) и под углом наклона = 40° – 60° к горизонту (рисунок 7.2).

Рисунок 7.2 – Линейная пространственная засечка
Работа GPS основана на простой геометрической идее – определении координат местоположения по расстояниям до спутников. Координаты приемника вычисляются на основе измеренных расстояний до группы спутников в космосе, спутники выполняют роль точно координированных точек отсчета. Например, расстояние от приемника до спутника А – 23000 км, то это значит, что приемник находится где-то на воображаемой сфере радиусом в 23000 км с центром, совпадающим со спутником А. Если расстояние от этого приемника до спутника В – 25000 км, можно сказать, что приемник находится на линии пересечения двух сфер, т.е. на окружности. Если до известно расстояние третьего спутника С, то можно определить две точки пересечения сферы С с окружностью, получившейся от пересечения сфер A и B. При этом обычно одна из двух полученных точек представляет неправдоподобное решение (рисунок 7.3). Если точно известна высота (например, морские корабли находятся на уровне моря), можно исключить одно из спутниковых измерений. Одна из сфер на рисунке 7.3 может быть заменена на сферу с центром в центре Земли и радиусом, равным сумме радиуса Земли и известной высотой наблюдателя.

Рисунок 7.3 – Определение места точки по расстояниям до спутников
Измерения расстояния до спутника сводится к определению времени прохождения радиосигнала от спутника до антенны приемника. Если точно определить момент времени, в который спутник начал посылать радиосигнал, а также момент, когда его принял приемник, и умножить скорость распространения сигнала на это время, получим расстояние до спутника. При этом часы приемника и передатчика должны быть очень точно синхронизованы, т.к. время прохождения сигнала от спутника к приемнику – всего несколько сотых секунды. Поэтому на спутниках GPS применяется способ измерения времени, основанный на атомном стандарте частоты, который обеспечивает ход бортовых часов спутника с наносекундной точностью.
Главной трудностью при измерении времени прохождения радиосигнала является точное выделение момента времени, в который сигнал передан со спутника. Для этого аппаратура спутников и приемники одновременно генерируют одну и ту же последовательность псевдослучайных кодов, повторяющуюся каждую миллисекунду. Приемник получает код от спутника и определяет сдвиг своей последовательности кодов по отношению к кодам спутника, т.е. как давно был сгенерировал этот же код. Выявленный сдвиг соответствует времени прохождения сигналом расстояния от спутника до приемника.
Если спутник и приемник рассинхронизованы всего на 0,01 сек., измерение расстояния будет произведено с ошибкой около 3000 км. На спутниках установлены несколько комплектов очень точных атомных часов. Поместить такие часы в недорогой компактный GPS-приемник невозможно. В приемниках используются недорогие кварцевые часы умеренной точности, а необходимая точность измерений достигается при помощи дополнительного измерения дальности еще до одного спутника.
Если три точных измерения определяют положение точки в трехмерном пространстве, то четыре неточных позволят исключить относительное смещение шкалы времени приемника. Рассмотрим способ определения поправки t при помощи дополнительного измерения расстояния до спутника, позволяющий синхронизовать часы приемника со спутниковыми часами. Для простоты изложения рассмотрим этот способ в двух измерениях.

Рисунок 7.4 – Определение поправки при помощи дополнительного измерения
Пусть измерены расстояния от спутников A, B и С до антенны приемника. Если часы приемника точно синхронизованы с часами на передатчиках (система GPS обеспечивает точную синхронизацию спутниковых часов между собой), три окружности с центрами в точках A, B и С и радиусом RA, RB, RC, пересекутся в одной точке (рисунок 7.4). Если часы приемника имеют уход t, радиус этих окружностей изменится на d = t c, и окружности уже не будут пересекаться в одной точке, а образуют некоторый «треугольник», внутри которого находится искомое местоположение.
Компьютер приемника подбирает поправку t, минимизируя E – площадь этого треугольника. Он продолжает корректировать время во всех измерениях до тех пор, пока не найдет решение, в котором все окружности проходят через одну точку. При определении местоположения в трехмерном пространстве необходимо выполнить четыре измерения. Необходимость в четырех измерениях сказывается на оборудовании GPS-приемников. Если требуется выполнять непрерывное местоопределение в реальном времени, то используют приемники, имеющие по крайней мере четыре канала измерений, т.е. с каждым из четырех спутников постоянно работает отдельный канал приема и первичной обработки сигналов.
Как узнать координаты в космическом пространстве спутника, двигающегося с большой скоростью и удаленного на тысячи километров? Спутники GPS движутся по высокой 18000-км орбите, т.е. полностью вне земной атмосферы. Полет спутника по орбите вокруг Земли в этом случае будет описываться относительно простыми уравнениями, поэтому движение спутников GPS – вполне предсказуемое. Орбиты известны заранее, а приемники имеют "альманах", размещаемый в памяти их компьютеров, из которого известно, где будет находиться каждый спутник в любой момент времени.
Чтобы сделать систему более совершенной, движение спутников GPS находится под постоянным контролем специальных наземных станций слежения. Обращаясь вокруг планеты один раз за 12 часов, спутники GPS проходят над контрольными станциями дважды в сутки. Это дает возможность точно измерять их высоту, положение и скорость. После того, как станции определили параметры движения спутника, они передают эту информацию обратно на спутник, заменяя ею в памяти бортового компьютера прежнюю. Далее эти небольшие поправки вместе с дальномерными кодовыми сигналами будут непрерывно передаваться спутником на Землю. Спутники GPS передают не только псевдослучайный дальномерный код, но также и информационные сообщения о своем точном положении на орбите и о состоянии своих бортовых систем. Все виды приемников GPS используют эту информацию вместе с информацией, заключенной в альманахе, для того, чтобы установить точное положение каждого спутника в космическом пространстве.

Рисунок 7.5 – Формат навигационных данных GPS
Существуют два источника погрешностей, которые очень трудно избежать. Наиболее существенные из погрешностей возникают при прохождении радиосигналом ионосферы Земли – слоя заряженных частиц на высоте от 120 до 200 км. Эти частицы влияют на скорость распространения света, а следовательно, и на скорость распространения радиосигналов GPS. Это вносит погрешности в вычисления расстояний до спутников, поскольку они построены на предположении, что скорость распространения радиоволн постоянна.
Существуют два метода, которые можно использовать, чтобы сделать ошибку минимальной. Во-первых, можно предсказать, каково будет типичное изменение скорости в обычный день, при средних ионосферных условиях, а затем ввести поправку во все наши измерения.
Другой способ заключается в сравнении скоростей распространения двух сигналов, имеющих разные частоты несущих колебаний. Таким образом, если мы сравним время распространения двух разночастотных компонент сигнала GPS, то сможем выяснить, какое замедление имело место. Этот метод корректировки достаточно сложен и используется только в более совершенных, "двухчастотных" приемниках GPS.
После того, как сигналы GPS пересекли ионосферу, они входят в слои атмосферы, в которых происходят различные погодные явления. Водяные пары в атмосфере также могут влиять на радиосигналы. Ошибки по величине схожи с ошибками, вызываемыми ионосферой, но их почти невозможно скорректировать. К счастью, их суммарный вклад в погрешность местоположения значительно меньше, чем ширина обычной улицы.

Атомные часы на спутниках также имеют небольшие погрешности. Специальные станции следят за этими часами и могут настроить их, если выявится уход. Приемники GPS могут выдавать ошибки: при округлении результатов математических операций, из-за электрических помех и т.п. Еще один источник погрешностей – многолучевой прием. Он возникает, когда сигналы, передаваемые со спутника, многократно отражаются от окружающих предметов и поверхностей до того, как попадают на антенну приемника
Для достижения наибольшей точности в дорогих приемниках GPS учитывается геометрический принцип "Geometric Dilution of Precision – GDOP" (геометрический фактор снижения точности). В зависимости от взаимного расположения спутников на небосводе геометрические соотношения, которыми характеризуется это расположение, могут многократно увеличивать или уменьшать все неопределенности.
В зависимости от угла между направлениями на спутники область пересечения размытых окружностей (область неопределенности местоположения) может быть либо аккуратным небольшим квадратиком, либо сильно растянутым и неправильным четырехугольником. Чем больше угол между направлениями на спутники, тем точнее определение места. Поэтому хорошие приемники снабжают вычислительными процедурами, которые анализируют относительные положения всех доступных для наблюдения спутников и выбирают из них четырех кандидатов, расположенных наилучшим образом.
Результирующая погрешность GPS определяется суммой погрешностей от различных источников. Вклад каждого из них варьируется в зависимости от атмосферных условий и качества оборудования. Кроме того, точность может быть целенаправленно снижена Министерством обороны США в результате установки на спутниках GPS режима S/A – селективного доступа. Этот режим разработан для того, чтобы не дать возможному противнику тактического преимущества в определении местоположения с помощью GPS. Когда этот режим установлен, он создает наиболее существенную компоненту суммарной погрешности GPS.
В настоящее время существует около тысячи различных моделей GPSприемников, выпускаемых более чем полутора сотнями компаний. В России наибольшую популярность завоевали портативные навигаторы Garmin и Magellan. Существует большое разнообразие моделей в ценовом диапазоне от 170 до 450 долларов. Приемники другой группы — GPS II, III, V, StreetPilot, StreetPilot ColorMap – имеют широкие картографические возможности и обладают расширенным набором функций для навигации в автомобиле, большей массой (250–500 г) и относительно высокой стоимостью (от 300 до 1200 долларов).
На рисунке 7.7. показан приемник Garmin GPS 72 и его основные интерфейсные страницы. Круговая диаграмма на рисунке 7.7-а отображает схематичное расположение спутников, гистограмма со столбиками указывает уровень сигнала от каждого из них. Контурный силуэт столбиков означает, что навигатор принимает сигнал спутника, но не использует его в целях местоопределения.

а) б) в) г)
Рисунок 7.7 – Портативный приемник GPS: а) – Magellan Meridian Color и Garmin GPS 72;
б) – информационная страница; в) – страница карты;
г) – страница компаса
Активно используемый сигнал показывается темным столбиком. Внизу дисплея высвечиваются текущие координаты – широта и долгота. Треугольная метка на рисунке 7.7-б указывает текущее местоположение и всегда находится в конце постоянно записываемого трека. Вверху дисплея — поле данных, которое можно конфигурировать по своему усмотрению. При необходимости на странице карты могут отображаться сохраненные в памяти прибора маршруты или треки. Предусмотрены три вида ориентации карты: на север, по курсу или вверх. С помощью страницы компаса можно точно ориентироваться в движении и знать направление на выбранную точку.
Промежуточное положение занимают навигаторы серии GPS 12. Существуют приемники, предназначенные для работы с ноутбуками и КПК. Они не имеют навигационного экрана, и все вычисления выполняются на компьютере. Например, Garmin GPS 35, похожий на мышь без кнопок, подключается к компьютеру через COM- или USB-порт и запитывается либо от автомобильного прикуривателя, либо от USB-порта. Он комплектуется магнитом (для установки, например, на крышу автомобиля) или присосками (на ветровое стекло или иллюминатор).
Тема 8. Растровые ГИС: модель данных и алгоритмы анализа
Растровая модель пространственных данных описывает характер исследуемого географического явления на всей. Растровая модель представляет окружающий мир в виде регулярной сети ячеек и является самой простой из распространенных моделей пространственных данных. Растр – набор данных, имеющих географический характер, значения которых организованы в прямоугольный массив объектов.

Рисунок 8.1 – Растровая модель данных
Разрешение растрового слоя можно охарактеризовать как минимальный линейный размер самого мелкой части географического пространства, для которого в слое записываются данные. В общем случае эта часть прямоугольная, но чаще всего - квадратная. Ориентация слоя – угол между действительным географическим севером и направлением, заданным линией столбцов растра. Зона растрового слоя – множество соприкасающихся клеток растра, имеющих одинаковое значение. Не все растровые карты содержат зоны - если клетки слоя содержат значения непрерывно изменяющегося в пространстве явления, этот слой не будет содержать зон. Значения ячеек - хранящаяся в слое информация о географическом явлении по строкам и столбцам. Ячейки, принадлежащие одной зоне, имеют одинаковые значения. Местоположение определяется упорядоченной парой ординат (номером сроки и столбца ячейки). Обычно известны реальные географические координаты нескольких углов растрового изображения.
В большинстве случаев с ячейкой растра связано только одно значение. Совокупность этих ячеек со связанными значениями образуют растровый слой. База данных может содержать несколько таких слоев, но они должны быть идеально выровнены. Каждый слой должен быть совместим с остальными слоями. Во всех слоях должно быть одинаковое количество строк и столбцов, и они должны отображать одно местоположение в пространстве.
Типы значений, содержащихся в ячейках, зависят как от типа моделируемых географических сущностей, так и от используемого программного обеспечения ГИС. Различные системы позволяются использовать разные классы значений: целые числа, вещественные числа, строковые значения. Большинство систем, работающих с растровыми изображениями, используют для значений ячеек только целые числа. Целые значения часто используются как коды, идентифицирующие класс покрываемой ячейкой территории:
|
2 |
2 |
2 |
2 |
2 |
|
1 1 1 |
1 |
2 |
2 |
2 |
|
1 |
3 |
3 |
3 |
|
|
1 |
3 |
0 |
0 |
Нет объекта
Сельхозземли
Лесные земли Автодороги
Рисунок 8.2 – Кодирование классов целыми числами
Растры чаще всего ассоциируются с представлением полей. Однако, возможно использовать растр для представления множеств дискретных объектов. Например, в растровом слое, имеющем целые значения ячеек, "1" может означать объект, а "0" - отсутствие объекта. При этом должны быть установлены правила, определяющие принадлежность объекта дискретному растровому слою:
- правило "большинства" – когда объект занимает более 50% покрываемой ячейкой площади, значение ячейки равно "1";
- правило "центральной точки" – когда в центральной точке ячейки есть объект, значение ячейки равно "1";
- правило "пересечения" – когда объект лежит на территории, покрываемой ячейкой, ее значение равно "1".
Так как ячейка растра может пересекать любое количество объектов, можно хранить количество объектов в каждой ячейке. Другое решение - присвоить идентификаторы объектам. Тогда ячейка со значением "0" будет обозначать отсутствие объектов, а ячейки с каким-либо значением будут обозначать наличие объекта с идентификатором, равным значению ячейки. Если на территорию, покрываемую ячейкой, попадают несколько объектов, значение идентификатора берется от объекта, имеющего большую площадь пересечения. Таким образом, идентификатор объекта служит для связи растра с таблицей объектов.
Во многих случаях значение, присвоенное ячейке растра, не является верным для всей покрываемой ячейкой территории. Смешанная ячейка - ячейка, которой соответствуют несколько классов объектов. В некоторых растровых базах данных есть возможность хранить несколько значений в ячейке одного слоя, что позволяет кодировать принадлежность ячейке нескольких объектов. Однако эта опция не является широко распространенной в современном программном обеспечении растровых ГИС.
Дискретные растровые слои аналогичны слоям векторных ГИС. Представление непрерывных поверхностей – одна из наиболее мощных возможностей растровых ГИС. Определяют два типа поверхностей: скалярные поверхности имеют в точке одно значение – магнитуду; векторные поверхности имеют в точке магнитуду и направление.

Рисунок 8.3 – Скалярные и векторные поверхности
Скалярное значение – одно число, например, возвышение над уровнем моря. Векторное значение имеет количественную характеристику и направление. Векторное поле является одним из примеров многокомпонентной поверхности, одно значение которой может быть выражено двумя растровыми слоями. Например, в ArcInfo существует различие между двумя видами феноменов, представляемых непрерывными поверхностями. Первый из них отражает измерение изменяющихся уровней, концентраций, температур и т.п. Второй тип представляет отношение между точками пространства и феноменом. Например, карты ветров, утечки нефти, распространения эпидемии.

Рисунок 8.4 – Скалярные и векторные поверхности в ГИС ArcInfo
Рассмотрим несколько примеров и определим, являются данные дискретными или непрерывными.
Данные дистанционного зондирования об уровне радиации, поступающие с одного канала искусственного спутника Земли в виде восьмибитового числа (0..255).
Классифицированное изображение, на котором ячейки растра, полученного со спутника, ассоциированы с одним из классов, обозначающих разнообразное использование земель. Например, "1" – города, "2" – сельскохозяйственные земли, "3" – моря, реки и озера.
Цифровая модель местности. Значение ячейки растра соответствует возвышению над уровнем моря точки в пространстве, соответствующей центральной точке ячейки.
Растровый слой дорог, где значение ячейки, равное "1", обозначает наличие дороги, а "0" – ее отсутствие.
При использовании растровой модели данных теряются мелкие детали. Но растровая модель имеет мощные аналитические возможности, и это преимущество гораздо значительнее, чем недостаток точности представления пространственных данных. Для сложного манипулирования растром на локальном, фокальном, зональном уровнях, для описания характеристик растров, для поиска взаимосвязей используются встроенные в ГИС математические функции и операторы.
При работе с растровыми географическими данными важно иметь процедуры автоматического описания содержания растрового слоя. Для растрового слоя или любой зоны слоя могут быть вычислены статистические характеристики, включающее среднее значение, медиану, наиболее часто встречающееся значение, дисперсию и другие статистические характеристики. Для нескольких слоев может быть проведено их статистическое сравнение, например, при помощи регрессионного или дисперсионного анализа.
Локальные операции создают новый растровый слой из одного или нескольких входных слоев. Значение ячейки нового слоя зависит только от значений ячеек входных слоев, имеющих те же растровые координаты. Обратите внимание, что применение арифметических операций требует наличия соответствующей шкалы измерений. Если значениями ячеек являются коды классов, бессмысленно применять к ним математические или статистические функции.
Перекодирование – класс локальных операций – использует только один входной слой. В качестве примера можно привести присвоение новых значений ячейкам путем присвоения значений классам, построенным на основе старых значений. Так, ячейки со значениями от 0 до 99 принимают значение "1", от 100 до 200 – значение "2", а более 200 – значение "3". Другой пример – сортировка уникальных значений, обнаруженных в растре и их замена на новые упорядоченные значения. Так, уникальные значения 0, 2, 5, 8 будут соответственно заменены на 0, 1, 2, 3.
|
|
|
|
Особую значимость в ГИС-анализе имеют оверлеи растров. Эти операции используют в качестве входных несколько растровых слоев, отсюда они и получили такое название. В некоторых ГИС, работающих с растровыми данными, встроен ряд математических функций для использования в оверлейных операциях. Процесс математического "наложения" слоев в ArcInfo называется алгеброй карт. Когда выходное значение зависит от двух или нескольких входных слоев, говорят, что происходит оверлей, "наложение" растров. Это похоже на наложение полигонов в векторной модели, но так как растровая модель значительно проще векторной, результат может быть получен на порядки быстрее.
Рассмотрим несколько примеров.
1. Выходное значение соответствует арифметическому среднему значений входных слоев. Эта операция может быть полезна, когда во входных слоях содержатся наблюдения какого-либо явления за несколько лет, и нужно найти среднее за эти годы значения показателя.
2. Выходное значение соответствует наибольшему (или наименьшему) значению соответствующих ячеек входных слоев.
3. Слои могут быть скомбинированы при помощи арифметических операций (рисунок 8.6). Если x и y - входные слои, то примерами выходных слоев могут быть z1=x+y, z2=x*y, z3=x/y.
4. Слои могут быть скомбинированы с помощью логических условий. Например, если y>0 значение выходного слоя будет z=y, а иначе z=x.
5. Каждой уникальной комбинации значений может быть присвоен уникальный идентификатор. Эту операцию можно применить для классификации ячеек.
Алгебра карт обеспечивает исследователей большими функциональными возможностями для конструирования сложных алгоритмов анализа растровых пространственных данных. Это позволяет создавать очень модели пространственного распределения феноменов.

Рисунок 8.6 – Использование арифметических операций
В фокальных операциях значение ячейки выходного слоя зависит от значения самой ячейки и от значений соседних ячеек. В пакетах для работы с растровыми данными имеются разнообразные способы описания соседних ячеек: в виде прямоугольной матрицы, круга, клина и т.д. Для понимания процесса наиболее подходит квадрат, поэтому остановимся на нем.
Одним из видов фокальных операций является фильтрация, осуществляемая методом “скользящего окна”. Определим окно размером, например, 3 на 3 пиксела, которым мы будем “скользить” по всем ячейкам входного растра. Каждой клетке окна приписывается некоторый вес. При этом сумма весов во всех клетках должна составлять единицу. Ячейка выходного слоя соответствует центральной ячейке окна, поэтому размер ячейки всегда выбирают нечетным. Значение ячейки выходного слоя вычисляется как взвешенное среднее значений, попадающих в окно.
|
0 ,11 |
0,11 |
0,11 |
|
0,05 |
0,05 |
0,05 |
|
-0,1 |
-0,1 |
-0,1 |
|
0,11
|
0,11 |
0,11 |
0,05 |
0,6 |
0,05 |
-0,1 |
1,8 |
-0,1 |
||
|
0 ,11 |
0,11 |
0,11 |
0,05 |
0,05 |
0,05 |
-0,1 |
-0,1 |
-0,1 |
а) б) в)
Рисунок 8.7 – Фокальные операции и фильтры: а) – сглаживающий;
б) – сильно сглаживающий; в) – увеличивающий резкость
Путем изменения весов в клетках окна мы можем программировать различные эффекты. Во многих программах, работающих с растровыми изображениями, имеются встроенные фильтры. К основным фильтрам относятся сглаживание и выделение границ. Фильтр, показанный на рисунке 8.7–а заменяет значения ячеек на среднее девяти ячеек (себя и соседей). Этот фильтр сильно сглаживает изображение.
Фильтр на рисунке 8.7-б вычисляет взвешенное среднее ячеек, считая вес самой ячейки в 12 раз больше веса её соседей. Этот фильтр несильно сглаживает исходное изображение. Фильтр на рисунке 8.7-в улучшает резкость изображения. В ГИС фильтры используются для улучшения детальности изображения в задаче ввода данных и для сглаживания изображения, если нужно из изображения выделить тренды.
Растровую модель геоданных можно использовать для представления однородных зон или классов почти также, как это делается при помощи полигонов. Зональные операции используются для анализа этих зон. В операциях выявления зон путем анализа смежных клеток растрового изображения определяются все зоны, имеющие одинаковое значение. Каждой такой зоне присваивается уникальный номер. Для каждой зоны вычисляется площадь или периметр и вычисленное значение присваивается каждой ячейке растра вместо номера зоны. Другой вариант – формируется таблица, в которой для каждого номера зоны указывается площадь и периметр.
Периметр вычисляется путем суммирования длин границ внешних пикселей зоны. Точность вычислений площади и периметра сильно зависит от ориентации зоны. Также могут вычисляться расстояние пикселей от границы зоны, определяться форма зоны. Последняя операция выполняется сравнением периметра зоны и квадратного корня из её площади. Если их отношение разделить на 3,54, мы получим число, изменяющееся от 1 для окружностей (наиболее компактная форма размещения пикселей) до 1,13 для квадратов. Большее значение этого числа соответствует более вытянутым зонам.
Тема 9. Физическая организация пространственных данных ГИС
В геоинформационных системах широко распространена растровая модель данных. Растры применяются для хранения и обработки данных дистанционного зондирования, для представления цифровых моделей рельефа, при визуализации геоданных и т.д. Существует множество вариантов кодирования растровых структур. Некоторые из них более экономно расходуют память, другие позволяют получать более быстрые алгоритмы. Растровая модель соответствует двумерному ячеистому изображению, которое хранится в памяти компьютера в виде одномерной последовательности значений. Растровые изображения обычно разлагаются по строке сверху – слева. Далее будут описаны другие способы эффективного представления растров.
В некоторых форматах графических файлов используется сжатие изображения, основанное на замене длительных последовательностей повторяющихся значений парой <значение, количество повторов> (рисунок 2.18-а). Географические данные обычно автокоррелированны. В растровой модели это означает, что соседние ячейки имеют большую вероятность быть одинаковыми, чем разобщенные. При обычном порядке сканирования в конце каждой строки происходит скачок на начало следующей строки. Предложим простое изменение порядка сканирования. Нечетные строки будем кодировать слева направо, а четные – в обратном направлении (рисунок 2.18-б). Направление сканирования напоминает движение быка, вспахивающего поле. Отсюда название этого способа– Boustrophedon (греч. – бык, вспахивающий поле). Теперь при переходе к новой строке первая ячейка является смежной последней ячейке старой строки. Так в линейном разложении растра сохраняется автокорреляция и повышается эффективность кодирования.

AAAA BBBA AABB BAAA 16 байт
AAAA ABBB AABB AAAB 16 байт 4A 3B 3A 3B 3A 8 байт
5A 3B 2A 2B 3A 1B 12 байт
Рисунок 9.1 – Порядки сканирования растров, их линейное разложение и сжатие: а) обычный порядок; б) Boustrophedon
Порядок сканирования Мортона (назван по имени Гая Мортона, впервые использовавшего этот способ в Canada GIS) основан на иерархическом разбиении карты. В предыдущих способах сканирования учитывалась автокорреляция значений ячеек только по одному направлению (по строке). Географические объекты образуют на растровом изображении пятна. В порядке Мортона предпринимается попытка сканирования ячеек таким образом, чтобы охватить линией обхода эти двумерные пятна.
Для растра размером 2 x 2 применяется обычный порядок сканирования. На следующем уровне матрица размера 4 x 4 складывается из четырех матриц размера 2 x 2, расположенных в таком же порядке, как ячейки матрицы 2 x 2 (рисунок 2.19). Аналогично формируется линия сканирования любой матрицы порядка 2n. Матрица формируется уровень за уровнем, повторяя один и тот же шаблон размера 2 x 2. При сканировании растра по Мортону линия сканирования представляет собой фрактал. Недостатки сканирования по Мортону очевидны. Во-первых, присутствуют скачки, например, от ячейки 7 к ячейке 8. Во-вторых, таким способом можно кодировать только растры размера, кратного двум.
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рисунок 9.2 – Порядок сканирования растра по Мортону
Рассмотрим следующий способ сканирования, в котором отсутствуют скачки между ячейками. На рисунке 2.20 ячейки растра сканируется по линии Пеано. Имеется базовый П-образный шаблон, который поворачивается от уровня к уровню так, чтобы обеспечить непрерывность линии сканирования.
При работе с растровыми данными важной является задача определения местоположения ячейки в последовательном файле по растровым координатам и наоборот. Для обычного порядка сканирования и для Boustrophedon – сканирования получение такого отображения не составляет труда. При сканировании по Мортону задача усложняется.
Рассмотрим пример. Пусть требуется по растровым координатам ячейки A(2, 3) определить ее номер в последовательности Мортона. Для этого представим координаты A в двоичной системе счисления и на их основе сформируем число N так, что координаты столбца ячейки A задают нечетные биты N, а координаты строки – четные биты. Получившееся число N=( 1 1 0 1 )2=13 соответствует позиции ячейки A в последовательности Мортона.
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
AAAAABBBBBAAABAA
5A 5B 3A 1B 2A
Рисунок 9.3 – Порядок сканирования растра Пеано
Обратная задача решается похожим способом. Пусть ячейка B записана в десятой позиции последовательности Мортона. Представим ее номер в двоичной системе счисления и разделим четные и нечетные биты между растровыми координатами столбца и строки ячейки: N=10=(1010)2 . Получим растровые координаты ячейки A(3, 0).
Рассмотренные выше порядки сканирования растровых изображений дают незначительные различия в компрессии данных. Основное преимущество Мортон-сканирования и других иерархических структур данных заключается в более быстром доступе к данным. Информация распределена по карте неравномерно. Увеличение разрешения растрового изображения приводит к увеличению размеров файлов, а уменьшение – к потере информации. Далее пойдет речь об адаптивных методах представления растровых данных с разной плотностью информации.
На рисунке 2.21 изображена растровая матрица размера 16 x 16, в которой содержатся 255 значений “A” и одно “B”. Индексируем растр следующим способом. Разделим матрицу на четыре подматрицы размера 8 x 8 и нумеруем их 0, 1, 2, 3 в порядке Мортона. Назовем подматрицу гомогенной, если в ней содержатся одинаковые значения. Будем рекурсивно разбивать негомогенные подматрицы до тех пор, пока не достигнем гомогенности всех подматриц. Таким способом получим адаптивное разрешение растрового изображения, где участки с меньшей плотностью информации представлены крупными блоками ячеек, а с большей плотностью – мелкими блоками ячеек.
Идея выделения гомогенных блоков растра тождественна кодированию растра по Мортону. Гомогенный блок растра размера m x m при сканировании по Мортону соответствует коду <m2,A>.

Рисунок 9.4 – Разбиение растра на гомогенные блоки
Соответствие двумерных растровых координат ячейки и адреса ячейки в последовательном файле похоже на аналогичное преобразование при кодировании растра по Мортону. Единственное отличие в том, что используется система счисления с основанием четыре. В примере на рис. 4 ячейка “B” имеет код 0311. В двоичной системе счисления N=0311=(00110101)2. Разделим биты между растровыми координатами и выясним, что ячейка лежит в четвертой строке и седьмом столбце.
Представленные таким способом растровые данные соответствуют квадродереву, вершина которого – исходное изображение, а листья – гомогенные блоки ячеек. При кодировании квадродеревьев ячейки на каждом уровне могут содержать либо значение гомогенного блока, либо указатель на следующий уровень. Дерево, показанное на рисунке 2.22 может быть представлено в виде линейной последовательности следующим образом.

Рисунок 9.5 – Кодирование квадродерева
Как уже отмечалось выше, основное преимущество иерархической организации данных в ГИС заключается в пространственном упорядочении информации и более быстром ее поиске. Поэтому рассматриваются две задачи ГИС, связанные с индексированием квадродеревьями: первая – поиск всех частей карты с заданным значением и вторая – определение содержимого некоторой ячейки.
Обозначим n – число уровней квадродерева (тогда размер растра 2n*2n) и через m – число листьев в дереве. Чтобы найти части карты с некоторым значением B, необходимо проверить каждый лист дерева, что потребует m шагов. Определение значения ячейки происходит путем спуска по квадродереву до тех пор, пока не будет получен гомогенный блок. В худшем случае, когда ячейка находится на самой вершине дерева (как, например, ячейка B на рисунке 2.21), поиск займет n шагов. Сравним теперь трудоемкости обеих задач на квадродереве с трудоемкостями этих задач при различных вариантах сканирования растра.
Таблица 9.1
|
Структура данных |
Поиск частей с заданным значением |
Определение значения ячейки |
|
Квадродерево |
M |
n |
|
Обычный порядок |
4 n2 * |
1 ** |
|
Boustrophedon |
m *** |
m **** |
|
Мортон |
m *** |
m **** |
Примечание: * – проверяется каждая ячейка матрицы; ** – непосредственное вычисление позиции ячейки; *** – число цепочек примерно соответствует числу листьев; **** – проверяется каждая цепочка.
Существуют различные модификации квадродеревьев, позволяющие, например, эффективно индексировать трехмерные данные (при этом куб рекурсивно делится на восемь частей). При кодировании глобальных данных в проекции Меркатора, представленных в растровой форме, существует проблема различий в форме и размерах ячеек, что приводит к отклонениям в модели. Проблема может быть решена путем представления данных в иерархической форме. Для этого строится глобальная тесселяция: земная поверхность проецируется на октаэдр, содержащий восемь пронумерованных треугольников. Далее каждый треугольник делится на четыре треугольника соединением отрезками середин его сторон. Получившаяся модификация квадродерева позволяет получать разрешение 1 метр при уровне вложенности дерева, равном 20.
Иерархическая организация данных позволяет получать быстрые способы доступа к пространственным данным. Рассмотрим теперь некоторые алгоритмы ГИС на квадродеревьях: вычисление площади, оверлейный алгоритм и алгоритмы определения смежности ячеек.
Чтобы определить площадь ячеек с некоторым значением в растровом слое, необходимо обойти дерево и подсчитать количество ячеек, кодированных этим значением, взвешенное площадью ячейке на данном уровне дерева. Вычислим, например, на карте 1 (рисунок 2.23) площадь ячеек со значением “A”. Площадь SA = 1*(Count leaf (00,02,03,32)) + 4*(Count leaf (2)) = 8.
|
A |
A |
A |
B |
Карта 2 |
1 |
2 |
2 |
2 |
|
A |
A |
B |
B |
1 |
1 |
2 |
2 |
|
|
A |
A |
B |
B |
1 |
2 |
2 |
2 |
|
|
A |
B |
B |
B |
2 |
2 |
2 |
2 |
Карта 1
![]()

Рисунок 9.6 – Оверлейная операция на квадродереве
Оверлейная задача на квадродеревьях заключается в совмещении квадродеревьев двух карт и получении нового квадродерева, индексирующего обе карты. Для этого требуется одновременно обойти оба дерева, следуя ветвям, существующим в обоих деревьях. В тех узлах, где у одного из деревьев будет отсутствовать ветвление, значение атрибута переносится на все последующие подуровни. В результате образуется “широкое” дерево, содержащее оба атрибута (рисунок 2.23).
Многие операции ГИС, работающие с иерархическими структурами данных, требуют наличия способов определения смежности ячеек. Для этого будем использовать представление координат ячеек в системе счисления с основанием 4 и разделять биты так, как это делалось в сканировании растра по Мортону. При этом используется tesseral – арифметика, в которой перенос между разрядами осуществляется через две позиции. Например, разность 1000 – 1 = 0010 , а сумма 1 + 0001 = 0100.
Будем различать два случая: когда проверяемые ячейки имеют коды одинаковой и разной длины. Блоки одинакового размера являются смежными, если их представления в tesseral – арифметике отличаются на 1 или 10. Например, блоки 01 и 03 являются смежными, так как 0011 – 0001 = 10. Блоки 033 и 211 также смежные, так как 001111 + 10 = 100101. Блоки 01 и 30 не являются смежными, так как 1100 – 0001 = 1001.
Для определения смежности блоков разного размера коды приводятся к основанию 2. Далее с кодом большей длины суммируются 01 и 10. Из получившихся четырех кодов отбрасываются как невозможные все отрицательные (по переносу). Оставшиеся коды сдвигом вправо приводятся к длине кода меньшей длины. Два блока являются смежными, если трансформированный и обрезанный код большей длины равен короткому коду.
Например, требуется определить, являются ячейки 02 и 2 смежными. Приведем коды в двоичной системе: 024 = 00102 , 24 = 102 . Прибавим к длинному коду 01 и 10. Получим 0010+1=0001, 0010+10=1000, 0010–10=0000. Разность 0010–1 отрицательная, эта комбинация отбрасывается как невозможная. Выбрав два старших разряда из оставшихся результатов, получим коды 002=04 и 102=24. Один из получившихся кодов равен короткому коду, поэтому ячейки 2 и 02 являются смежными.
В векторных ГИС пространственные индексы используются для более быстрого доступа к объектам на определенном участке карты. Индексирование пространственных объектов позволяет уменьшить вычислительную сложность процедур поиска пересекающихся и вложенных объектов, поэтому индексы являются важной частью алгоритмов оверлея полигонов.
Процесс построения индекса для цифровой карты включает следующие шаги. Сначала для каждого объекта базы данных находится наименьший лист квадродерева, полностью включающий объект. Некоторые крупные объекты могут лежать более чем в одном квадранте первого уровня квадродерева. В этом случае объекты помечаются значением “NULL”. Остальные объекты помечаются кодом включающего листа квадродерева. Затем объекты сортируются по возрастанию получившегося ключа, а сам индексный файл в свою очередь индексируется обычным способом (рисунок 2.24).
Построенные таким способом индексы используются для поиска объектов, пересекающих заданный полигон или линию. Для этого определяется минимальный лист квадродерева, включающий заданный объект. Поднявшись из полученного узла до вершины дерева и выполнив обход поддерева, корнем которого является этот узел, получим список листьев дерева, внутри которых объекты могут пересекаться с заданным объектом.
Очевидно, пространственные индексы, построенные на квадродеревьях, более эффективны по сравнению с независимым упорядочиванием объектов по x и y, так как в этом случае учитывается пространственный характер данных. Индексирование квадродеревьями наиболее целесообразно для мелких объектов (особенно для точек). Большим объектам обычно соответствуют крупные блоки. Для них часто требуется определять пересечения с другими объектами.
|
|
|
Рисунок 9.7 – Индексирование цифровой карты квадродеревом
Проблему индексации крупных объектов можно решить с использованием R-деревьев (R – rectangle, прямоугольник), в которых также используется концепция минимального вмещающего прямоугольника. Здесь требуется найти два прямоугольника таких, что внутри них расположено максимально возможное число объектов. При этом нужно стремиться, чтобы количество объектов в прямоугольника должно быть приблизительно одинаковым. Прямоугольники могут пересекаться, но площадь пересечения должна быть настолько малой, насколько возможно. Далее эта процедура рекурсивно повторяется (рисунок 2.25).

Рисунок 9.8 – Индексирование цифровой карты R–деревом
Тема 10. Модели 3D – поверхностей в ГИС
В отличие от цифровых представлений точечных, линейных и площадных объектов, трехмерные объекты требуют особых форм представления, т.к. их местоположение описывается не только двумерными, но и высотными координатами. К наиболее распространенному типу трехмерных объектов относится топографический рельеф земной поверхности. При помощи трехмерных объектов могут быть также смоделированы карты плотности населения, атмосферного давления, влажности и т.п. Однако трехмерные модели традиционно связывают с цифровыми моделями рельефа (digital elevation model - DEM). Далее мы будем рассматривать модели рельефа, подразумевая возможность моделирования и других непрерывных феноменов и явлений.
Цифровые модели рельефа позволяют по конечному набору выборочных точек определять возвышение, крутизну склона, направление ската в произвольной точке на местности. Возможно выявление особенностей местности – бассейнов рек, дренажных сетей, пиков, впадин и т.п. Такие модели широко применяются во многих процедурах ГИС-анализа: при выборе места строительства зданий и коммуникаций, в анализе дренажных сетей, в анализе видимости, при выборе маршрута движении по пересеченной местности.
Особенно широко цифровые модели рельефа применяются в гидрологии.
Поверхности являются непрерывными феноменами в противоположность дискретным объектам, выражаемым точками, линиями и полигонами. Но существуют способы представления поверхностей, в которых используется конечное количество точек. Разные подходы к выбору узловых точек, в которых известно значение возвышения поверхности, определяют две наиболее распространенные модели данных. В геоинформационных системах поверхности обычно описываются при помощи растровых моделей и триангуляционных сетей. В растровых моделях выборочные точки расположены в узлах регулярной растровой решетки, а в триангуляционных сетях – располагаются нерегулярно так, чтобы наилучшим образом “обогнуть” поверхность (отсюда название – triangulated irregular networks – TIN).
При моделировании непрерывных поверхностей также являются важными вопросы оценки возвышения поверхности в произвольной ее точке. В растровых моделях используется билинейная интерполяция, а триангуляционных сетях возвышение определяется из уравнения плоскости, заданной вершинами треугольника.
В обеих моделях могут быть вычислены производные к поверхностям, из которых наиболее часто используются угол и экспозиция склона. Угол наклона поверхности в некоторой точке обычно измеряют в градусах или процентах. Плоские регионы имеют нулевую крутизну склонов. Чем круче горы, тем больше угол наклона. Экспозиция склона характеризует направление наибольшего угла наклона в некоторой точке поверхности. Следует помнить, что подобные измерения имеют смысл только для прямоугольных систем координат, а для системы координат широта/долгота результаты будут неточны (особенно в северных широтах).
Исходными данными для создания цифровых моделей рельефа могут быть данные полевых измерений, изолинии рельефа топографических карт, профили фотограмметрических стерео–изображений, гидрографические и гипсометрические карты и т.п. Обратная операция также возможна. На основе растровых DEM или триангуляционных сетей можно построить карты рельефа в изолиниях, рассчитать профили поверхности между заданными точками. Эффектным средством визуализации топографической поверхности являются трехмерные изображения.
Растровые цифровые модели местности
В случае, когда выборочные точки располагаются в узлах регулярной решетки, цифровая модель рельефа может быть построена при помощи растровой модели. Как известно, эта модель имеет преимущества перед объектными моделями в простоте алгоритмов обработки и анализа данных, обусловленной простотой организации данных. Растровые DEM являются самым простым способом представления топографических данных и широко распространены.
Чтобы оценить возвышение произвольной точки, нужно определить, лежит точка в каком-нибудь узле сети. Если так, то значение возвышения выбирается непосредственно из базы данных. В противном случае необходимо выбрать процедуру оценки возвышения по ближайшим узловым точкам. Как грубое приближение можно использовать высоту ближайшей узловой точки (рисунок 10.1-а). При этом значения высоты будут изменяться скачкообразно.

а) б) в)
Рисунок 10.1 – Оценка возвышения в произвольной точке: а) – по ближайшей узловой точке; б) – аппроксимация МНК; в) – билинейная интерполяция
Более гладкую поверхность можно получить, если аппроксимировать значения высоты в области, ограниченной четырьмя точками сети (рисунок 10.1-б). При этом необходимо учитывать, что полученная методом наименьших квадратов поверхность не обязательно проходит через узлы решетки, следовательно, в полученной поверхности вдоль соединяющих узлы линий будут разрывы. Будем искать приближение в окрестности узлов в виде плоскости Z (x, y) = c0 + c1x + c2y. Коэффициенты c0 + c1x + c2y находятся из СЛАУ.
i 1 i x i y c 0 i z
2
x x xy c1 zx .
i y i xy i y 2 c 2 i zy
i i i i
Поверхность без разрывов (с разрывом первой производной) можно получить, используя билинейную интерполяцию (рисунок 10.1-в). Выберем такую систему координат, что x1 = x2 , y2 = y3, x3 – x2 = 1, y2 – y1 = 1. Найдем возвышения Z5 = Z2 + (Z3 – Z2) x и Z6 = Z1 + (Z4 – Z1) x. Тогда Z = Z6 + (Z5 – Z6) y.
Наклон и направление в произвольной точке растровой DEM вычисляются с использованием соседних точек. Обычно используется окно 3 x 3. Наклон поверхности определяется как отношение изменения возвышения к изменению горизонтального местоположения и выражается в процентах или градусах (рисунок 10.2-а). Наклон измеряется в направлении наиболее крутого изменения возвышения. Чаще всего это направление не совпадает с направлением строк и столбцов растра (рисунок 10.2-б). Для вычисления угла наклона будем использовать формулу Sград = arctan [(Z/x)2 + (Z/y)2]1/2 . Направление склона (aspect) определяется как A = arctan [– (Z/y) / (Z/x)].
![]()
![]() S%h/l100%;
S%h/l100%;
Sград arctan(h/l).
а) б)
Рисунок 10.2 Вычисление наклона поверхности: а) – вычисление угла наклона поверхности; б) – направление наиболее крутого изменения возвышения.
Рассмотрим следующий способ определения угла наклона поверхности в растровой ячейке DEM. Вычислим отношение Z /x по значениям ячеек Z4 и Z5 , а Z /y – по ячейкам Z4 и Z5 (рисунок 10.3-а). В этом примере расстояния между центроидами ячеек равно десяти, поэтому Z/x = (49 – 40) /
20 = 0.45; Z/y = (45 – 48) / 20 = –0.15. Отсюда угол наклона поверхности Sград = arctan [(0.45)2 + (–0.15)2]1/2 = 25.38. Вычислим направление склона: A = arctan [ – (–0.15) / (0.45) ] = 18.43.

Рисунок 10.3 – Вычисление угла наклона поверхности в растровой ячейке по 4 соседним: а) – схема вычисления; б) –ядра преобразования.
Вычислить угол наклона поверхности во всех ячейках растрового слоя можно при помощи двух преобразований, ядра которых приведены на рисунке 10.3-б. Эти преобразования позволяют получить для ячейки значения
Z/x и Z/y , по которым вычисляется угол наклона. Исходный растровый слой m x n точек обрабатывается скользящим окном размера 3 x 3. В результате этой фокальной операции получается растровый слой, в ячейках которого содержатся значения угла наклона, и имеющий размер (m – 2) (n – 2).
Как видно из рисунка 10.3-а, при определении угла наклона поверхности в растровой ячейке DEM по четырем соседним не используются угловые ячейки окна – z1, z3, z6, z8. Рассмотрим способ вычисления угла наклона поверхности по конечным разностям третьего порядка (рисунок 10.4-а).
![]() а)
б)
а)
б)
Рисунок 10.4 – Вычисление угла наклона поверхности в ячейке по конечным разностям 3-го порядка: а) – схема вычисления; б) – ядра преобразования.
Здесь Z/x = [1*(47–42) + 2*(49–40) + 1*(52–44)] / 80 = 0.39; Z/y = [1*(47–52) + 2*(45–48) + 1*(42–44)] / 80 = –0.16. Отсюда угол наклона поверхности Sград = arctan [(0.39)2 + (–0.16)2]1/2 = 22.9, а направление склона А = arctan [ – (–0.16) / (0.39) ] = 22.36.
По растровому слою, содержащему углы наклона поверхности, может быть построена тематическая карта. Для этого задается легенда – шкала углов наклона с соответствующими цветами отображения. Пример такой тематической карты приведен на рисунке 10.5-а. На физических картах с целью улучшения восприятия изображения рельеф показывается с отмывкой – пластическим полутоновым изображением рельефа путем наложения теней. На цифровых картах такой эффект можно получить, раскрашивая ячейки растровой DEM в соответствии с экспозицией склонов. Если источник освещения расположен на северо-западе, светлыми цветами раскрашиваются ячейки с экспозицией 270–360, темными цветами – 90–180, средними цветами – 0–90и 180–270 (рисунок 10.5-б).

Рисунок 10.5 Карты рельефа: а) – тематическая карта углов наклона топографической поверхности; б) – изображение рельефа с отмывкой по экспозиции
Растровые DEM могут использоваться в гидрологии для построения моделей стока, определения водоразделов рек (рисунок 10.6). Направление стока из ячейки растра определяется ее высотой и высотой соседних ячеек. При этом могут рассматриваться все восемь соседей (движение королевы) или четыре соседа по вертикали и горизонтали (движение ладьи). Будем считать, что из данной ячейки имеется сток на соседнюю, если высота соседней ячейки меньше высоты других соседних ячеек и высоты данной ячейки.
В растровых DEM анализ видимости по вычислительной сложности значительно проще. Анализ видимости - операция обработки цифровых моделей рельефа, обеспечивающая оценку поверхности с точки зрения видимости или невидимости отдельных ее частей путем выделения зон и построения карт видимости с некоторой точки обзора или множества точек, заданных их положением в пространстве (рисунок 10.7-а).

Рисунок 10.6 Использование растровых DEM в гидрологии: а) - направление стока, водоразделы и дренажная сеть б) –карта дренажной сети и водоразделов.
Пусть наблюдатель находится в ячейке с высотой 100 м. Справа от наблюдателя расположены ячейки с высотами { 110; 125; 115; 160; … }. Легко видеть, что ячейки с высотами 110, 125, 160 будут наблюдателю видны, а ячейка с высотой 115 – нет. На рисунке 10.7-б показана трехмерная модель с рассчитанными для заданного положения наблюдателя зонами видимости.

а)
Рисунок 10.7 – Анализ видимости: а) – схема определения видимости;
б) – пример зон видимости для заданного положения наблюдателя (белый цвет)
Нерегулярные триангуляционные сети (TIN)
Нерегулярные триангуляционные сети (Triangulation Irregular Network – TIN) являются альтернативой растровым DEM и используются во многих геоинформационных системах, системах автоматизированного картографирования, пакетах построения контуров. Модели TIN разработаны в 1970-х годах как простой способ построения поверхностей по нерегулярно расположенным точкам.
Модель TIN обладает некоторыми преимуществами перед растровыми DEM. В первую очередь, расположение точек адаптировано к местности: в равнинных участках точки расположены реже, а гористых – чаще. Выборочные точки соединяются прямыми отрезками, образующими треугольники, внутри которых поверхность задается плоскостью. Поверхность непрерывна, треугольники соединены между собой. Структуры данных в TIN-моделях более компактны и экономичны: TIN-модели из сотен точек может соответствовать растровая DEM из десятков тысяч точек. Несмотря не простоту модели, создание TIN требует решения ряда сложных задач: как размещать выборочные точки, как соединять точки в треугольники, как моделировать поверхность внутри треугольника.
Рассмотрим задачу выбора размещения точек триангуляции на следующем примере: имеется растровая DEM или оцифрованные изолинии рельефа, необходимо выбрать точки таким образом, чтобы наиболее точно представить поверхность в TIN-модели. Рассмотрим алгоритмы выбора точек DEM.
Алгоритм Фаулера – Литтла основан на поиске особых точек поверхности – пиков, хребтов, впадин и т.п. Поверхность проверяется скользящим окном размера 3 x 3. При этом соседи центральной ячейки помечаются плюсом, если их высота больше, и минусом если меньше. Очевидно, точка является пиком, если все восемь ее соседних ячеек помечены минусом. Аналогично, точка является впадиной, если все восемь ее соседних ячеек помечены плюсом. Точка является ущельем или перевалом, если плюсы и минусы вокруг точки образуют хотя бы два полных цикла:
{ + + – – – – + + } = 2 цикла; { + – + – + – + – } = 4 цикла.
Далее слой обрабатывается окном 2 x 2 таким образом, что каждая ячейка по очереди становится во все позиции окна. Точка является гребнем горы, если в каждом из четырех окон она не самая низкая. Аналогично, точка принадлежит протоку, если во всех четырех окнах она не самая высокая. Затем, начиная от ущелий или впадин, ищутся связные протоки, пока не будут достигнуты пики (поиск можно вести и в обратном направлении). В результате получаются соединенные линиями пики, протоки, впадины, ущелья и перевалы. По выбранным точкам создаются треугольники.
Алгоритм VIP (очень важная точка) в отличие от предыдущего алгоритма, в котором идентифицируются основные особенности местности, проверяет поверхность локально, используя окно 3 x 3. Это упрощение впервые использовано в ГИС ESRI Arc/Info. Ячейка в растровой DEM имеет восемь соседей, образующих четыре тройки (рисунок 10.8-а).
![]()
 Тройка 1: { 8 – 6 – 4 } Тройка
3: { 10 – 6 – 8 }
Тройка 1: { 8 – 6 – 4 } Тройка
3: { 10 – 6 – 8 }
б) а)
Рисунок 10.8 – Алгоритм VIP: а) – 4 тройки ячеек; б) –расчет вариаций
Для каждой тройки ячеек по соответствующей вариограмме рассчитывается коэффициент вариации (рисунок 10.8-б). Первая тройка имеет нулевой коэффициент вариации, вторая и четвертая – низкий, а третья – высокий коэффициент вариации. Далее оценивается средняя вариация значения узла растровой DEM. Узлы с высокими показателями вариации включаются в результирующее разбиение, остальные отбрасываются.
Третий алгоритм выбора точек триангуляции основан на оптимизации существующего разбиения. Для заданной растровой DEM требуется найти такое подмножество точек (заданной мощности), что при соединении их линиями в треугольники получится как можно лучшее представление поверхности.
По узлам регулярной сети легко построить исходное разбиение на треугольники. В начале работы алгоритма разбиение полностью соответствует исходной растровой DEM. Далее все точки разбиения поочередно проверяются следующим способом. Точка временно удаляется, соответственно изменяется и разбиение. Затем определяются треугольники, содержащие удаляемую точку, оценивается разность возвышений этой точки, полученных из DEM и из трех верши треугольника. Эта разность записывается в базе данных и удаленная точка восстанавливается. Когда таким образом будут обработаны все точки, нужно удалить точки с наименьшими значениями запомненных в базе данных разностей.
После того, как выбрано необходимое количество узлов TIN, нужно выбрать способ разбиения поверхности на треугольники. При этом желательно получить близкие к равносторонним треугольники, чтобы произвольная точка поверхности была как можно ближе к узлам TIN, где значения возвышения известны точно. Рассмотрим два способа разбиения на треугольники.
Триангуляция может быть получена путем упорядочивания точек по расстоянию между ними. Для этого вычисляются и сортируются по возрастанию расстояния между всеми парами точек. Ближайшие пары точек соединяются линией, если эта линия не пересекает полученные на предыдущих шагах линии. Процесс завершается, когда невозможно создать ни одной новой линии. В результате получится TIN-разбиение, в котором будет много остроугольных треугольников.
Этого недостатка лишена триангуляция Делоне. По определению три точки формируют треугольник в триангуляции Делоне тогда и только тогда, когда в окружности, описанной вокруг этого треугольника нет других точек разбиения. Разобьем поверхность на области, в которых каждая точка расположена ближе всего к некоторому узлу сети – генерирующей точке. Полученные границы называют полигонами Тиссена или полигонами Вороного. Две точки соединяются линией в триангуляции Делоне, если их полигоны Тиссена имеют общую границу. Этот метод позволяет получить требуемые “жирные” треугольники.

Рисунок 10.9 – Алгоритм Уотсона: а) – исходное разбиение; б) – выбор треугольников, описанная вокруг которых окружность содержит новую точку;
в) – удаление треугольников; г) – разбиение выпуклого многоугольника
Триангуляция Делоне может быть получена при помощи алгоритма Уотсона. В начале работы этого алгоритма создается супертреугольник, содержащий все точки разбиения. Точки последовательно добавляются в существующее разбиение. Опишем процедуру образования нового разбиения при добавлении новой точки (рисунок 10.9). Сначала выбираются треугольники, описанная вокруг которых окружность содержит добавляемую точку. По определению эти треугольники не могут входить в триангуляцию Делоне, поэтому их следует удалить из разбиения. Выбранные треугольники разбиваются на отрезки, дублирующиеся отрезки удаляются. Оставшиеся отрезки формируют границу выпуклого многоугольника, который разбивается на новые треугольники простым соединением вершин с добавляемой точкой. По окончании работы алгоритма супертреугольник удаляется.
Существует два основных способа хранения TIN: по треугольникам и по точкам. При кодировании сети по треугольникам для каждого треугольника в базе данных создается запись, содержащая его уникальный номер, координаты трех его вершин, а также номера трех смежных с ним треугольников (рисунок 10.10-а). Во втором способе (рисунок 10.10-б) для каждой точки разбиения сохраняется ее уникальный номер, координаты и список точек, с которыми она соединена прямыми (по часовой стрелке).

|
ID треугольника |
10 |
|
Координаты точек |
(X 10, 1 ; Y 10, 1 ; Z 10, 1 ) (X 10, 2 ; Y 10, 2 ; Z 10, 2 ) (X 10, 3 ; Y 10, 3 ; Z 10, 3 ) |
|
Сосед №1 |
1 |
|
Сосед №2 |
4 |
|
Сосед №3 |
7 |
|
ID |
8 |
|
Координаты точки |
(X 8 ; Y 8 ; Z 8 )
|
|
Соседи |
6, 7, 9, 4, 5 |
а)
Рисунок 10.10 – Модели хранения TIN: а) – по треугольникам; б) – по точкам
Рассмотрим способ вычисления наклона поверхности и экспозиции склона в TIN-модели. Для этого вычислим нормали к каждому треугольнику разбиения. Треугольник задается тремя точками (xa,ya), (xb,yb), (xc,yc). Тогда нормаль P к плоскости треугольника может быть выражена через векторное произведение двух его сторон как
(yb ya) (zc za) (zb za) (yc ya) pa
P (zb za) (xc xa) (xb xa) (zc za) pb . (xb xa) (yc ya) (yb ya) (xc xa) pc
Теперь вычислим направляющие косинусы и проекцию нормали P к горизонтальной плоскости:
pa pb pc pa pb g ; h ; i ; e ; f .
![]()
![]()
![]()
![]()
![]() pa2 pb2 pc2 pa2 pb2 pc2 pa2 pb2 pc2 pa2 pb2 pa2 pb2
pa2 pb2 pc2 pa2 pb2 pc2 pa2 pb2 pc2 pa2 pb2 pa2 pb2
После этого можно вычислить угол наклона поверхности треугольника и экспозицию склона к северному направлению (рисунок 10.11):
arccos(i) arccos pc ; arccos( f ) arccos pb .
![]()
![]() pa2 pb2 pc2 pa2 pb2
pa2 pb2 pc2 pa2 pb2

Рисунок 10.11 – Графическое представление положения угла наклона и экспозиции склона треугольника
Возвышение произвольной точки внутри треугольника определяется по уравнению плоскости, заданной вершинами треугольника. Плоскость с нормальным вектором (мы его уже вычисляли) P = {pa, pb, pc}, проходящая через точку M0(x0, y0, z0), описывается уравнением pa ( x – x0) + pb ( y – y0) + pc ( z – z0) = 0. Отсюда по известным значениям x и y находятся возвышения произвольных точек.
Анализ стока в триангуляционных сетях осуществляется на основе рассчитанных для каждого треугольника угла наклона и экспозиции склона. При этом можно выделить два подхода к моделированию стока. В первом из них с треугольниками сети обращаются как с дискретными элементами: вода стекает с одного треугольника на другой в направлении максимального наклона. Второй способ предполагает работу с поверхностью как с мозаикой плоскостей треугольников. Здесь вода течет в треугольнике, собирается и движется вдоль дуг.
По растровым DEM и по триангуляционным сетям можно построить карты распределения характеристики по территории. Для этого нужно задать список значений z, по которым будут проведены изолинии. Например, можно взять максимальное и минимальное значения характеристики, разделить полученный интервал на несколько частей и с полученным шагом провести изолинии.
Изолинии заданной высоты строятся следующим способом. Рассмотрим все ячейки растровой DEM (или все треугольники триангуляционной сети). Будем искать пересечения ячеек (треугольников) с горизонтальной плоскостью Z=const. Из полученных отрезков нужно собрать полилинии (рисунок 10.12). Для этого следует объединять смежные отрезки. Полилинии могут быть сглажены, например, при помощи сплайн–функций.
100 100 100

100 130 50
Рисунок 10.12 – Построение изолиний в растровой модели рельефа (а) и в TIN (б)
Цифровые модели местности могут использоваться для построения профилей местности между выбранными точками. Для решения этой задачи нужно найти точки пересечения линии профиля с ячейками DEM или треугольниками TIN и оценить возвышение поверхности в полученных точках. Полученные точки соединяются и образуют полилинию: вдоль горизонтальной оси показывается протяженность профиля, а вдоль вертикальной – возвышения (рисунок 10.13).

Рисунок 10.13 – Профиль топографической поверхности
Тема 11. Геодезия и цифровая фотограмметрия в ГИС
Геодезия – наука, изучающая форму и размеры Земли и разрабатывающая вопросы создания координатной плановой и высотной основы для детального изучения физической поверхности Земли методами топографии и картографии – имеет исключительную важность для создания геоинформационных систем. Основной объем данных ГИС имеет пространственный характер, и чтобы обеспечить возможность выполнения даже простейших картометрических измерений по этим данным, требуется задать некоторую систему координат. В ГИС для пространственной привязки данных традиционно используются топографические карты, хотя развитие в последнее десятилетие систем GPS и ГЛОНАСС и их высокая экономическая эффективность подталкивает разработчиков ГИС к использованию автономных систем определения координат.
Геодезической основой топографических съемок всех масштабов является в нашей стране Государственная геодезическая сеть (ГГС). Плановая сеть создается методами триангуляции, полигонометрии, трилатерации и их сочетаниями, а высотная сеть создается построением нивелирных ходов и сетей геометрического нивелирования.
По последовательности и точности определения пунктов, по длинам сторон треугольников государственная геодезическая сеть делится на четыре класса, обозначаемые цифрами 1, 2, 3, 4. Наивысшей по точности является триангуляционная сеть 1-го класса, в которой выполняются астрономические и гравиметрические определения координат. Эта сеть используется для изучения фигуры Земли, распространения единой системы координат на всю территорию России. На ее основе строятся плановые геодезические сети последующих порядков.
Для того, чтобы использовать в ГИС данные дистанционного зондирования Земли, выполнять по ним измерения длин и площадей, отображать результаты дешифрирования на топографической основе, космические и аэрофотоснимки, имеющие различные геометрические искажения, должны пройти фотограмметрическую обработку.
Система прямоугольных координат на плоскости может задаваться тремя способами. Первый способ заключается в установке местоположения точки отсчета системы, ортогональных осей oX и oY, направления оси OY (левая или правая система), масштаба координат вдоль осей. При наличии координатных осей для определения координат точки C нужно опустить перпендикуляры из этой точки на оси oX и oY и измерить их длину. Длина перпендикуляра к оси oX равна координате Y, длина перпендикуляра к оси oY координате X точки. Указанный способ часто используется в геодезии (например, так задается система прямоугольных координат Гаусса).
Во втором способе проводятся две взаимно перпендикулярные системы равноудаленных параллельных линий, параллельных осям координат. Каждой линии приписывается значение соответствующей координаты. Таким способом на топографических картах задается километровая сетка.
В третьем способе указываются значения координат двух фиксированных точек. Этот способ используется на местности для определения системы прямоугольных координат. Для этого нужно найти несколько геодезических пунктов с известными координатами и определить положение новых точек относительно этих пунктов, выполняя некоторые измерения.
Определение координат произвольной точки по известным координатам других точек основывается на измерениях дирекционных углов и расстояний между точками. Дирекционный угол – угол между прямой, соединяющей эти точки, и прямой, параллельной оси абсцисс (в проекции Гаусса – вертикальной линии координатной сетки). Угол задается тремя точками: вершиной угла двумя точками, по которым находятся направления сторон угла. В простейшем случае в треугольнике хотя бы одна из трех точек не имеет координат и является определяемой. В общем случае определяемыми могут быть одна точка, две или три точки. Расстояние определяется по координатам двух точек, и в общем случае определяемыми могут быть одна или обе точки. Рассмотрим способы определения координат одной точки на основе трех элементарных измерений.
В первом элементарном измерении на пункте A с известными координатами (XА,YА) измеряется угол β между направлением с известным дирекционным углом αAB и направлением на определяемую точку P (рисунок 11.1). Дирекционный угол α направления AP получается по формуле AB .

0 YА 0 YB
Рисунок 11.1 – Элементарные измерения: углы и расстояния
Прямая AP, называемая линией положения точки P описывается уравнением Y YA tg X XA, где X и Y – координаты точек на прямой AP.
Для нахождения координат точки P одного такого уравнения недостаточно.
Во втором элементарном измерении определяется расстояние от пункта
A с известными координатами (XA, Ya) до определяемой точки P. Точка P лежит на окружности радиуса S с центром в точке A. Уравнение окружности имеет вид X XA2 YYA2 S2 . Для определения координат точки P одного уравнения окружности также недостаточно.
В третьем элементарном измерении на определяемой точке P измеряют угол β между направлениями на два пункта с известными координатами.
Для измерения углов и расстояний используются различные геодезические приборы. Расстояния раньше измеряли при помощи металлических штриховых лент со шпильками, рулеток длиной 5, 10, 20 и 50 м. Мерные линейные приборов изготавливались из инвара – сплава 64% стали и 36% никеля, имеющего коэффициент расширения в 40 раз меньше, чем у стали. Сейчас в основном используются оптические (в т.ч. и лазерные) дальномеры.
Для измерения горизонтальных и вертикальных углов на местности используются теодолиты. Основной рабочей мерой в теодолите служат горизонтальный и вертикальный круги с градусными делениями. Теодолитом измеряют и расстояния.
Тахеометр – геодезический прибор для измерения расстояний, горизонтальных и вертикальных углов – используется для вычисления координат и высот точек местности при топографической съемке местности. Различают оптические тахеометры и электронные тахеометры. В электронных тахеометрах расстояния измеряются по времени прохождения инфракрасного луча до отражателя и обратно или по сдвигу фаз. Дальность измерения зависит от типа отражателя. Для пленочных тахеометров дальность ограничена несколькими сотнями метров, для отражателя с призмой – до 10 километров.
Координаты X и Y точки P можно находятся из совместного решения двух уравнений, полученных из элементарных измерений. Взяв любые два элементарных измерения, получим простейшие способы определения координат точки, называемые геодезическими засечками. Два уравнения прямых дают прямую угловую засечку, по двум уравнениям окружности получают линейную засечку, по одному уравнению прямой и одному уравнению окружности – полярную засечку. Если на определяемой точке измеряется угол между направлениями на точки с известными координатами, получается обратная угловая засечка.
В полярной засечке исходными данными являются координаты точки A и дирекционный угол направления AB (или координаты пункта B), измеряемыми элементами являются горизонтальный угол β и расстояние S, а неизвестными элементами – координаты точки P (X, Y).
Для графического решения полярной засечки от направления AB откладывается угол β и проводится прямая AQ, а затем вокруг точки A проводится окружность радиусом S в масштабе карты. Точка пересечения прямой линии и окружности даст искомую точку P. Решим полярную засечку аналитически. Дирекционный угол α линии AР равен α= αAB + β. Запишем уравнения прямой AP и окружности радиуса S с центром в точке A:
Y YA tgX XA; (11.1)
X XA2 YYA2 S2

0 YB 100 200
Рисунок 11.2 – Полярная засечка
Решим систему уравнений методом подстановки. Подставим значение (Y – YA) из первого уравнения во второе и вынесем за скобки (X–XA)2:
(X–XA)2 (1 + tg2 α)= S2.
Используя тригонометрическое тождество 1 + tg2α = 1 / Cos2α , получим: (X–XA)2 =S2 Cos2α , откуда X – XA = S Cos α . Подставим это значение в первое уравнение и получим ординату Y–YA = S Sin α. Обозначим приращения (X–XA)=ΔX и (Y–YA)= ΔY. Полярная засечка однозначно решается по формулам:
α= αAB + β;
X S cos(); Y S sin() ; (11.2)
X XA X ; Y YA Y .
При помощи полярной засечки решается прямая геодезическая задача – вычисление координат точки (XB,YB), если известны координаты точки (XA,YA), расстояние между этими точками – SAB, а дирекционный угол равен α. Прямая геодезическая задача решается по формулам:
XB XA SAB cos(); YB YA SAB sin(). (11.3)
Обратная геодезическая задача заключается в вычислении дирекционного угла α и длины линии S, соединяющей две точки A и B с известными координатами (XА,YА) и (XB,YB). Для получения угла α можно вычислить угол arctg(Y /X) и определить квадрант, в который попадает точка (X,Y).
Если X<0, дирекционный угол α=180º+γ, иначе α=γ.

Рисунок 11.3 – Обратная геодезическая задача на плоскости
Пусть координаты Гаусса-Крюгера точки A – (5627301, 16494870), координаты точки B – (5637895, 16504224). Вспомним, что в системе координат Гаусса-Крюгера переменная X указывает расстояние точки от экватора, а Y – расстояние от осевого меридиана. Получим приращения координат X=10594, Y=9354. Отсюда расстояние между двумя точками A и B
![]() S
105942 93542 14132,59 метра,
угол γ равен 41º26’35”,
S
105942 93542 14132,59 метра,
угол γ равен 41º26’35”,
В примере на рисунке 2-Б дирекционный угол направления на точку B из точки A равен AB=135º. Этот угол можно определить, решая обратную геодезическую задачу. Тогда дирекционный угол направления из точки A на точку P найдем как α=AB–β= 135º–55º=80º. Воспользуемся формулами (1) для вычисления координат точки P:
XP=400+150*cos(80º)=426,04; YP=100+150*sin(80º)=247,72.
В случае прямой угловой засечки в двух точках A и B с известными координатами (XA,YA) и (XB,YB) измеряются углы A и B, каждый от своего направления с известным дирекционным углом. Графически решение представляет собой точку пересечения двух прямых, заданных точками A и B, через которые они проходят, и углами наклона. Дирекционный угол AP вычисляется по определенному ранее дирекционному углу линии AС и измеренному углу A: AP=AC +A. Аналогично находится угол BP=BC +B. Решим систему из двух уравнений прямых:
Y YA tgAPX XA
(11.4)
Y YB tgBPX XB.
Вычитая одно уравнение из другого, после несложных преобразований получим координаты точки P:
YB YAtgAP XA tgBP XB
X ![]() ; (11.5)
; (11.5)
tgAP tgBP
Y YA X X A tgAP .
В примере на рисунке 11.4 координаты точки A – (400,100), дирекционный угол на определяемую точку P равен 80. Точка B имеет координаты (300,200), а дирекционный угол на точку P равен 10. Используя формулу (11.5), определим координаты точки P – (421,221).

В линейной засечке измеряются расстояния SAP и SBP до определяемой точки от двух точек A и B с известными координатами (XA,YA) и (XB,YB). Графически решение находится как точка пересечения окружности с центром в точке А радиусом SAP и окружности с центром в точке B радиусом SBP. Этих точек пересечения окружностей получается две – Pлевая и Pправая (рисунок 11.5). Нужная точка выбирается по расположению (слева или справа) относительно прямой направления AB.

Рисунок 11.5 – Линейная засечка
Для аналитического решения линейной засечки решим обратную геодезическую задачу между точками A и B: определим дирекционные углы αAB и αBA, а также расстояние b между точками A и B. Вычислим углы βA и βB , воспользовавшись теоремой косинусов:
SBP b2 SAP2 2bSAP cos(A ); (11.6)
SAP b2 SBP2 2bSBP cos(B ) .
Далее нужно найти дирекционные углы сторон AP и BP. Если определяемая точка расположена справа от линии AB, то αAP= αAB+βA, αBP= αBA–βB. Если определяемая точка расположена слева от линии AB, то αAP= αAB–βA, αBP= αBA+βB. Теперь для определения координат точки P можно решить прямую геодезическую задачу из точки A на P и из точки B на P. Полученные два решения должны совпасть.
В примере на рисунке 11.5 дирекционный угол αAB=135º, угол βA=69,41º, угол βB=54,99º, а расстояние между точками A и B – 141,42 м. Решая прямую геодезическую задачу от точки A, получим координаты точки P – (457, 227).
Для определения относительного планового положения геодезических пунктов используется метод триангуляции, основанный на построении на местности систем примыкающих друг к другу треугольников, в которых измеряют их углы и длину хотя бы одной стороны треугольника, называемой базисом. Системы треугольников строят в виде цепей и сетей треугольников. Координаты пунктов триангуляции вычисляют на ЭВМ по программам, реализующим алгоритмы строгого уравнивания.
A Единичный ∆ P Цепочка Сеть

Рисунок 11.6 – Триангуляция
Трилатерация представляет собой сплошную сеть примыкающих друг к другу треугольников, в которых измеряются длины всех сторон. При этом как минимум две точки должны иметь известные координаты. Решение первого треугольника трилатерации, в котором известны координаты двух вершин и измерены стороны, выполняется по формулам линейной засечки. В каждом следующем треугольнике также становятся известны координаты двух вершин и длины сторон, поэтому их решение также выполняется по формулам линейной засечки.
Полигонометрия – метод определения координат геодезических пунктов путем проведения на местности полигонометрического хода – ломаной линии, в которой измеряются все углы и стороны. На рисунке 11.7 показан полигонометрический ход AabcB, проложенный между опорными пунктами A и B. Здесь AM и AN – исходные направления, a, b и c – вершины хода, βi – углы, а Si – стороны хода. Полигонометрическая сетью называется система связанных между собой ходов.

Рисунок 11.7 – Полигонометрия
Цифровая фотограмметрия
Фотограмметрия – техническая дисциплина, основной целью которой является определение вида и размеров какого-либо объекта путем изучения и измерения его фотографического изображения, – нашла наибольшее применение в топографии, где объектом изучения и измерения является местность. Задача фотограмметрии – заменить полевые измерения, необходимые для создания карты, измерениями аэрофотографии или космического снимка в камеральных условиях при помощи специальных фотограмметрических приборов и программного обеспечения.
Методы фотограмметрии начали разрабатываться в середине XIX века с возникновением техники фотографии. До появления самолетов фотограмметрия использовалась для поиска взаимосвязей между обычными фотографиями и большого практического значения не имела. С развитием воздухоплавания в начале XX века возникла потребность совмещать сделанные с летательного аппарата фотографии с картами. В аналоговой фотограмметрии для построения топографических карт и трехмерных объектов по двум перекрывающимся снимкам использовались оптические и механические приборы. В аналитической фотограмметрии некоторые дорогие компоненты системы фотограмметрической обработки заменялись компьютером, а аналоговые измерения – математическими вычислениями.
Цифровая фотограмметрия работает с цифровыми изображениями, получаемым путем сканирования аэрокосмических фотографий или непосредственно с цифровой камеры. Методы цифровой фотограмметрии позволяют еще сильней автоматизировать процесс подготовки фотокарт и ортопланов, а также получать новые ГИС-продукты, например, цифровые модели рельефа. Часть фотограмметрии, изучающая способы определения высоты объекта и измерения характеристик рельефа, называется стереофотограмметрией.
Использование данных дистанционного зондирования Земли значительно упрощает и удешевляет процесс создания топографических карт и дает принципиально новые возможности для тематического картографирования. Космический снимок можно рассматривать как некоторую картографическую проекцию земной поверхности. Если преобразовать снимок таким образом, чтобы его «проекция» соответствовала проекции создаваемой карты или слоя ГИС, этот снимок можно будет непосредственно использовать совместно с другими слоями. Так можно проводить ручное дешифрирование полученных из космоса фотографий по подложке, отображать на топографической основе результаты обработки и анализа снимков, совмещать при визуализации векторные карты и растровые снимки. Накладывая на фотокарту слои гидрографии и автодорог, получается весьма наглядный ГИС-продукт.
Непосредственно совмещать космические фотографии и карты нельзя, так как снимки содержат различные деформации. На геометрические искажения космических снимков влияет ряд факторов. На снимках в центральной проекции этими факторами являются угол наклона и кривизна Земли. На космических сканерных снимках факторов, влияющих на геометрию изображения, становится значительно больше. Если съемка нескольких последовательных сцен выполняется непрерывно во времени, большое значение имеет собственное вращение Земли, приводящее к деформации формы участков фотографируемой поверхности. Также необходимо учитывать время формирования строки, законы проецирования во время съемки, способ визуализации.
Поставщики космических снимков предоставляют пользователям изображения с различным уровнем коррекции. Например, уровень 1A сцены, полученной со спутника SPOT, означает изображение, полученное непосредственно с камеры, с выполненной радиометрической коррекцией. Изображения уровня 1B откорректированы с учетом вращения Земли, угла съемки.
Аэрофотоснимок – фотографическое изображение местности, полученное с самолета или другого летательного аппарата. Точки, лежащие на траектории полета самолета и в которых выполняются снимки, называются точками экспозиции. Масштаб изображения m – отношение расстояния между двумя точками на изображении к расстоянию между этими же точками на местности – определяется по формуле:
1 f
![]() ,
m H
,
m H
где f – фокусное расстояние камеры, H – высота полета.
Например, если высота полета самолета – 1000 метров, длина фокуса камеры – 15 сантиметров, то получаем масштаб снимка – 1 : 6667.

Рисунок 11.8 – Составление маршрутов и блоков
Маршрут состоит из нескольких снимков, сделанных на одной линии полета, обычно с перекрытием 60% (рисунок 11.8). Фотографии маршрута снимаются приблизительно с одной высоты и с постоянным расстоянием между точками экспозиции. Несколько маршрутов можно объединить в блок с перекрытием 20-30%. Чтобы трансформировать изображение в блоке так, чтобы они совмещались с точками на топографической поверхности, используется фотограмметрическая триангуляция.
В фотограмметрии используется несколько различных систем координат. Для определения положения элемента на растровом изображении используются координаты пикселя (r, c) – номер строки и номер столбца на растре. Нумерация строк и столбцов обычно ведется от верхнего левого угла. Позиция точки на изображении задается координатами изображения (x, y) в миллиметрах или в дюймах. В системе координат изображения точка (0, 0) располагается в центре изображения. Система координат на местности основана на некоторой картографической проекции, используются трехмерные координаты точки, выраженные в метрах или футах.
В геоцентрической системе начало координат расположено в центре референц-эллипсоида. Ось oZ совпадает с осью вращения Земли, ось oX проходит через Гринвичский меридиан перпендикулярно оси oZ, а ось oY перпендикулярна oX и oZ и образует с ними правую тройку.
Топоцентрическая система имеет начало координат в центре изображения, спроектированного на Земной эллипсоид. Ось oY ориентирована на север, ось oX – на восток, а по оси oZ откладываются вверх высоты.
Внутреннее ориентирование изображения восстанавливает перспективные отношения, существовавшие в момент съемки. Элементами внутреннего ориентирования называются переменные, определяющие положение центра проектирования относительно плоской системы координат оXY: фокусное расстояние f, и координаты главной точки. При фототриангуляции внутреннее ориентирование требуется, чтобы правильно установить внешнее ориентирование камеры.
Космические и аэрофотоизображения получаются проецированием лучей света, отраженных от объектов на поверхности Земли, через линзу на фотопленку или на матрицу светочувствительных элементов. Лучи распространяются по прямой и пересекаются в одной точке – центре перспективы или в фокусе. На плоскости, на которую проецируется действительное изображение поверхности Земли, размещаются светочувствительные элементы – фотопленка или матрица ПЗС-датчиков.
Мнимая фокальная плоскость называется плоскостью изображения. Центр перспективы, спроецированный на плоскость изображения, называется главной точкой изображения. Ортогональное расстояние от центра перспективы до плоскости изображения называется длиной фокуса линзы (рисунок 11.9-a).
![]() Плоскость кадра
Плоскость кадра
Поверхность Земли
а)
Рисунок 11.9 – Внутренняя геометрия изображения, сделанного камерой
На рисунке 11.9-б показаны восемь маркеров, зафиксированных на плоскости кадра камеры и видимых на каждом изображении. Координаты маркеров на изображении определяются при калибровке камеры или предоставляются поставщиком космического снимка. Координаты на растре (XF,YF) соответствуют номеру строки и столбца элемента. Для внутреннего ориентирования снимка нужно определить координаты маркеров (XF1,YF1)… (XF8,YF8).
Для трансформации снимка в систему координат изображения используют аффинные преобразования
x a0 a1X F a2YF , y b0 b1X F b2YF ,
где a0, a1, a2, b0, b1, b2 – коэффициенты аффинного преобразования, определяемые по измеренным координатам маркеров, (XF,YF) – координаты на растре, (x,y) – координаты на изображении.
Полученные коэффициенты аффинного преобразования позволяют преобразовать все пиксели исходного растра в систему координат изображения. Это преобразование выполняет перенос центральной точки пиксельных координат в центральную точку изображения и поворот снимка на некоторый угол так, чтобы направление строк и столбцов растра совпадали с осями oX и oY изображения.
X , номер столбца
![]() x
x
x
Рисунок 11.10 – Преобразование пиксельных координат в систему координат изображения
Основой этого этапа фотограмметрической обработки служат уравнения перехода от плоских координат растрового изображения к пространственным декартовым координатам объекта. Внешнее ориентирование снимка определяет связь растрового изображения и топографической координатной системы. Шесть переменных, определяющих позицию и ориентацию изображения в момент съемки, называют элементами внешнего ориентирования снимка.
Переменные X0 , Y0 , Z0 позицию точки центра перспективы снимка O в топоцентрической системе координат. Переменная Z0 показывает возвышение камеры над уровнем моря и зависит от используемого геодезического датума. Другие три элемента внешнего ориентирования являются угловыми и определяют положение плоскости изображения относительно плоскости топографической системы координат:
– угол поворота плоскости изображения вокруг оси oX фотографии; – угол поворота плоскости изображения вокруг оси oY фотографии; – угол поворота плоскости изображения вокруг оси oZ фотографии.

Рисунок 11.11 – Элементы внешнего ориентирования снимка
Элементы внешнего ориентирования снимка определяют из условий коллинеарности проектирующих лучей, если на снимке изображены не менее 3 опорных точек с известными геодезическими координатами:
r11(X X0) r21(Y Y0) r31(Z Z0)
x f ,
r13(X X0) r23(Y Y0) r33(Z Z0)
r12 (X X 0 ) r22 (Y Y0 ) r32 (Z Z0 ) y f ,
r13 (X X 0 ) r23 (Y Y0 ) r33 (Z Z0 )
где (x, y) – координаты изображения, (X, Y, Z) – геодезические координаты, f – фокусное расстояние, (X0, Y0, Z0) – геодезические координаты центра перспективы, r11…r33 – элементы 3х3-матрицы поворота, заданной углами ,,.
Для восстановления эпиполярных плоскостей стереопары, построения геометрической модели и получения стереоскопического изображения необходимо взаимное ориентирование одного снимка относительно другого. Снимки обычно лишь приблизительно горизонтальны, поэтому в начале процедуры взаимного ориентирования соответствующие проектирующие лучи двух снимков не пересекаются, что приводит к появлению вертикальных параллаксов. Горизонтальный параллакс можно устранить изменением высоты плоскости проектирования, вертикальный параллакс свидетельствует о неправильном взаимном ориентировании.
Приблизительная схема операций фотограмметрической обработки на примере системы PHOTOMOD показана на рисунке 11.12. Исходные снимки приводятся в цифровую форму при помощи сканера. Если для сканирования используется бытовые планшетные сканеры, имеющие невысокую точность, неравномерную скорость перемещения линейки светочувствительных датчиков и другие недостатки, приводящие к искажениям изображения, необходимо провести исправление сканированного снимка. Использование профессиональных фотограмметрических сканеров исключает операции корректировки сканированных изображений из технологической цепочки.
Исправленные снимки включаются в проект и формируется предварительно ориентированный блок. При этом задается тип проекта (моноблок, стереоблок, одиночный сканерный снимок), определяется система координат проекта, вводятся параметры съемочной аппаратуры. Затем проводится сбор данных для фототриангуляции. Выполняется внутреннее ориентрирование, вводятся и измеряются координаты опорных точек, межмаршрутные связи, связи между соседними изображениями в блоке, взаимное ориентирование.
Распределение и плотность опорных точек, получаемых путем опознания на снимке объектов с известными координатами, оказывает решающее влияние на точность фототриангуляции. Хорошо в качестве опорных точек использовать пункты государственной геодезической сети (если конечно детальность снимка это позволяет). Если пунктов геодезической сети недостаточно или их невозможно опознать на снимке, строят сети сгущения и определяют координаты легко опознаваемых объектов. Для измерения координат опорных точек можно использовать также профессиональные геодезические GPS-приемники, работающие в дифференциальном режиме.
Опорные точки не обязательно должны быть заданы для каждого изображения проекта. Возможность использовать для изображения координатную основу со смежных изображений дают связующие точки – опознанные и измеренные на двух или более изображениях объекты местности, координаты которых неизвестны и вычисляются в процессе фототриангуляции.
По измерениям опорных точек, выполненным на предыдущем шаге, выполняется уравнивание блока, вычисление элементов внешнего ориентирования и эпиполярное трансформирование. При неудовлетворительных результатах уравнивания возвращаются к сбору данных для фототриангуляции, проверяют и редактируют измерения. Обычно помимо опорных точек в проект вводят и измеряют дополнительные контрольные точки. По среднеквадратическим ошибкам в этих точках оценивают качество результатов уравнивания блока изображений.
Исходные снимки

TIN, DEM, 3D - вектора 3D - вектора Ортофотоплан
Рисунок 11.12 – Операции фотограмметрической обработки в PHOTOMOD
Результаты уравнивания используются для создания различных ГИСпродуктов. В режиме стереоизображения могут быть векторизованы трехмерные объекты, а также созданы 3D-модели TIN и DEM. Чтобы совместить несколько кадров в одно изображение, строится мозаика.
Тема 12. Картографические модели структуры явлений в ГИС
Карты, как особые модели окружающего мира, характеризуются рядом особенностей: непрерывностью, метричностью, обзорностью и наглядностью изображения, заданной картографической генерализацией, возможностью избирательного изображения объектов. Но карты обладают также важнейшими гносеологическими свойствами, позволяющими проводить по ним исследования географических объектов и явлений. В книге «Моделирование в картографии» В.С. Тикунов описывает множество математикокартографических моделей структуры географических явлений, их взаимосвязей и динамики. Отсылая изучающих к этому замечательному труду для подробного знакомства со всем разнообразием этих моделей, сосредоточимся в данной главе и в последующих двух главах на особенностях их реализации в геоинформационных системах.
Рассмотрим следующую практическую задачу. Имеется сеть из N метеорологических постов, на которых периодически измеряется температура воздуха. Известны точные координаты (xi, yi) i=1..N этих постов на географической карте; температуру в точке (xi, yi) обозначим zi. Площадь карты (экстент) задана прямоугольником (xmin, ymin)–(xmax, ymax). Данные со всех наблюдательных пунктов поступают в обрабатывающий центр, где на их основе требуется составить карту погоды.

Рисунок 12.1 – Построение карты температуры при помощи тренда
Данные измерений на постах представляют значения двумерной функции пространственного распределения F(x,y) в некоторых выборочных точках. Чтобы изучить общие закономерности пространственного расположения этих явлений на исследуемой территории, часто используются модели аппроксимации, в которых поверхность раскладывается на фоновую и остаточную составляющие, по которым создаются две производных карты. Карта тренда передает распределение в пространстве ведущего фактора, а карта остаточных поверхностей показывает размещение в региональных аномалий, вызванных влиянием неучтенных в модели факторов.
Для построения модели тренда чаще всего используют полиномы сте-
m m пени m : T Ci, j X iY j , где T – картографируемый показатель, Ci,j – коэф-
i 0 j 0
фициенты полинома, (X,Y) – координаты точек на карте. Задав вид аппроксимирующей функции T(X,Y) и используя метод наименьших квадратов, определим по опорным точкам (xi, yi, zi) коэффициенты Ci,j полинома T. Полученная таким способом аппроксимирующая функция T(X,Y) позволяет оценить значение картографируемого показателя в любой точке карты (при правильном размещении опорных точек). В выборочных точках вычисляются невязки – отклонения T(X,Y) от реальной поверхности: i=zi – T(xi, yi). По этим отклонениям строится остаточная поверхность R(X,Y).
Поверхности T(X,Y) и R(X,Y) на карте могут быть отображены в виде изолиний. Для этого наложим на карту на карту регулярную решетку, в узлах которой вычислим аппликаты трендовой и остаточной поверхности. Получим растровое представление поверхностей, или DEM. Чтобы получить из DEM изображение трендовой поверхности в виде изолиний, определим min T(X,Y) и max T(X,Y), установим шаг изолиний T и получим множество плоскостей {Z=min T(X,Y), Z=min T(X,Y)+ T , … , Z=max T(X,Y)}. Найдем точки пересечения этих плоскостей с ребрами регулярной решетки и соединим полученные точки в изолинии. Изолинии для остаточной поверхности формируются аналогично.
Аппроксимируем функцию пространственного распределения температуры плоскостью F(x,y)=A+Bx+Cy, седловой функцией F(x,y)=A+Bx+Cy+Exy, квадратичной поверхностью F(x,y)=A+Bx+Cy+Dx2+Exy+Fy2, кубической поверхностью F(x,y)=A+Bx+Cy+Dx2+Exy+Fy2+Gx3+Hx2y+Ixy2+Jy3. В таблице 12.1 приведены координаты постов (xi, yi), значения измеренной на них температуры zi, расчетные значения тренда T(xi,yi) и остаточной поверхности i, полученные сглаживанием эмпирических данных разными полиномами.
Таблица 12.1
|
xi |
yi |
zi |
Плоскость |
Седло |
Квадратичная |
Кубическая |
||||
|
T(xi, yi) |
i |
T(xi, yi) |
i |
T(xi, yi) |
i |
T(xi, yi) |
i |
|||
|
120 |
85 |
5 |
3,68 |
-1,32 |
4 |
-1 |
4,54 |
-0,46 |
5,13 |
0,13 |
|
120 |
90 |
6 |
4,78 |
-1,22 |
4,94 |
-1,06 |
5,78 |
-0,22 |
6,09 |
0,09 |
|
120 |
95 |
7 |
5,88 |
-1,12 |
5,88 |
-1,12 |
6,82 |
-0,18 |
6,84 |
-0,16 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
140 |
100 |
9 |
8,42 |
-0,58 |
8,58 |
-0,42 |
9,42 |
0,42 |
9,12 |
0,12 |
|
140 |
105 |
10 |
9,52 |
-0,48 |
9,84 |
-0,16 |
10,38 |
0,38 |
9,79 |
-0,21 |
![]()
![]()
![]() 105
105
105
105
85 85
120 140 120 140
![]()
![]() 105
105
105
105
![]() 85
85
85
85
120 140 120 140
![]()
![]() 105
105
85
120 140 120 140
105
 85
85

|
120 140 120 |
140 |
Рисунок 12.2 – Тренды T(x,y) и остаточные поверхности R(x,y) температуры
Рассмотрим модели пространственного расположения точечных объектов на примере моделирования размещения населения. В качестве исходных данных здесь можно использовать цифровые топографические карты. На картах масштаба 1 : 1000000 населенные пункты представлены площадными и точечными объектами (пунсонами). Размер и знак пунсона зависят от численности населения. На картах масштаба 1 : 200000 все населенные пункты показаны площадными объектами. Заменим площадные объекты слоя населенных пунктов их центроидами и введем для каждого пункта количество проживающих в нем жителей Pi.
В картографии давно используется способ построения карт плотности размещения объектов, называемый методом «скользящего окна». Картонный лист, в котором прорезано прямоугольное отверстие, перемещался горизонтально и вертикально над картой. При этом подсчитывалось и заносилось в таблицу количество попадающих в «окно» объектов. Соседние окна брались с перекрытием – эта простейшая свертка обеспечивала фильтрацию таблицы.
В современных ГИС легко реализовать подобный алгоритм. Будем перемещать окно Wx: xmin<x<xmax , ymin<y<ymax вдоль экстента карты с шагом (x,y) и подсчитывать для попадающих внутрь окна точек Pi . Тогда плотность населения в окне С=Pi /(x*y). Полученная DEM может быть конвертирована в изолинии способом, описанным в предыдущем разделе.

Рис. 12.3. Карта плотности населения Красноярского края
Полученная таким способом карта плотности населения Красноярского края (рисунок 12.3) хорошо отражает как агломерационные, так и линейные схемы размещения населения. Особенно высока плотность населения возле крупных населенных пунктов, вдоль Транссибирской железной дороги, автодорог с покрытием. В северных районах края население в основном распределено вдоль берегов Енисея и Ангары.
Равномерность распределения населенных пунктов по территории оценивается следующим образом. Возьмем в качестве эталона равномерного расположения идеальную гексагональную решетку Кристаллера. В качестве показателя равномерности будем использовать коэффициенты
100 1 12 1 12 2
![]()
![]() V d , d
i1 di , 12 i1 (di d) , (12.1)
V d , d
i1 di , 12 i1 (di d) , (12.1)
12
где di –расстояния между шестью пунктами, ближайшими к центральному, и между этими пунктами и центральным.
Коэффициенты (12.1) рассчитываются для каждого населенного пункта. Так как пункты представлены точечными объектами, между ними легко вычисляется расстояние. Выберем шесть населенных пунктов, ближайших к текущему, и при помощи алгоритма коммивояжера построим кратчайший замкнутый путь обхода этих пунктов. Длина ребер полученного шестиугольника даст оставшиеся шесть расстояний.
d
![]() d12
d12
d
) )
Рис. 12.4. Модель равномерности размещения точечных объектов:
а) – идеальная гексагональная решетка; б) – реальная решетка
В узлах гексагональной решетки значения коэффициента V равны нулю. Поэтому населенные пункты, в которых значения V малы (0–40%), распределены на карте равномерно. Показателем неравномерности распределения населенных пунктов являются высокие значения V (60–100%). Населенные пункты с вычисленными коэффициентами V образуют нерегулярную сеть. С целью построения изолиний эта сеть либо разбивается на треугольники, либо преобразуется в регулярную сеть при помощи интерполяции.
На рисунке 12.5 показана карта равномерности размещения населенных пунктов центральной части Красноярского края. Легко видеть, на однородных территориях, (равнинах с одинаковой плотностью и транспортным сообщением), населенные пункты в основном размещены равномерно. При этом линейные схемы размещения населенных пунктов, связанные с транспортными магистралями, влияния на равномерность расселения практически не оказывают.

Рисунок 12.5 – Равномерность размещения населенных пунктов
Для освоения природных ресурсов одним из важнейших факторов являются трудовые ресурсы. Большая часть населения Красноярского края проживает в его южных районах, что затрудняет освоение северных территорий Нижнего Приангарья.
В задачах картографирования распространения населения по территории традиционно используется понятие демографического потенциала. По аналогии с формулой тяготения сила взаимодействия населенных пунктов
Ni N j может быть записана
как Fi, j
![]() k , где Ni
и Nj – численность населения
k , где Ni
и Nj – численность населения
Di, j
в двух населенных пунктах, Di,j –расстояние между ними, а k – параметр модели. Потенциал произвольной точки j на карте соответствует степени взаимодействия этой точки со всеми населенными пунктами: Pj Ni / Dik, j . Для
i
картографирования трудового потенциала в узлах регулярной решетки вычисляется потенциал поля расселения и затем строится карта изолиний. На рис. 4.2. показана карта потенциала поля расселения для значения k=1,2.
 P, чел./км
P, чел./км
Рисунок 12.6 – Карта потенциала поля расселения
Задача классификации географических объектов на основе некоторого множества их характеристик широко распространены в геоинформатике. Классификация территорий подразумевает разбиение исходного множества районов на заданное или неизвестное число групп на основании некоторого математического критерия качества классификации. Для решения таких задач используются алгоритмы прикладной статистики: регрессионный анализ, факторный анализ, метод главных компонент.
Многочисленные статистические данные, связанные обычно с административными территориальными единицами, могут использоваться для классификации районов края. В качестве пространственной привязки может использоваться слой границ цифровой карты, на котором в соответствии с легендой карты выделяются полученные в результате классификации группы. Рассмотрим один из наиболее простых методов классификации географических объектов – "вроцлавская таксономия", заключающийся в выделении классов на основе вычисленных «расстояний» между объектами в ортонормированном пространстве их характеристик. Пусть имеется n территориальных единиц, характеризующихся набором из m показателей. Набор показателей для i-ой территории записывается как вектор-строка xi1, xi2 , xi3 K xim , i 1Kn, а для всех территорий – в виде матрицы размером m xn:
x11 x12 L x1m 21 22 L x2m x x
X . (12.2)
L L L L
xn1 xn2 L xnm
Характеристики объектов могут выражаться величинами, имеющими разный масштаб, или вообще несравнимыми величинами. Поэтому сначала нормируем исходные данные по дисперсиям:
xij
xj
xij ![]() ,
где i 1Kn, j 1Km . (12.3)
,
где i 1Kn, j 1Km . (12.3)
j
Характеристики объектов могут быть зависимыми. С целью перехода к независимым показателям выполняется процесс ортогонализации матрицы. Рассмотрим столбцы нормированной матрицы Xнорм как векторы. Тогда матрица Xнорм может быть записана в виде Xнорм X1, X2,L X m . Ортогональную матрицу будем искать в виде X~ X~1, X~2,L X~m .
Пусть X~1 X1. Вектор X2 может быть разложен на составляющие, одна из которых направлена по вектору X~1, а другая ортогональна к нему:
X2 a12X~1 X~2, где скалярное произведение X~1, X~2 0. Умножая скалярно обе части уравнения на X~1, получим X2, X~1 a12X~1, X~1. Отсюда a12 XX~12,,XX~~11 и
~2 2 12 ~1. Аналогично раскладывается вектор X3:
X X a X
X3 a13X~1 a23X~2 X~3 , где X~1, X~3 0, X~2, X~3 0; (12.4)
13 X3, X~1 23 X3, X~2 ~3 3 13 ~1 23 ~2. (12.5)
a
~1 ~1,
a
X~2,
X~2,
X
X
a X
a X
X , X
~k k kl11 lk ~l , alk
X~kl , X~~ll . Вычисляя
после-
В общем виде имеем X X a X X , X
довательно векторы X~i , i 1Km, получим искомую матрицу X~ , которая будет использоваться для вычисления расстояния между объектами.
По независимым характеристикам вычисляется расстояние между объектами. При этом объекты рассматриваются как точки в m-мерном пространстве характеристик, а значения характеристик объектов – как координаты этих точек. Расстояние между объектами вычисляется по известной формуле
m
![]() dik
(x x ) . Симметричная матрица таксонометрических расстояний
принимает вид
dik
(x x ) . Симметричная матрица таксонометрических расстояний
принимает вид
|
d21 Dd31 M d1n |
d12 0 d32 M d2n |
d13 d23 0 M d3n |
L L L O L |
M 0 |
(12.6) |
Группирование объектов в классы производится с использованием метода динамических ядер. Термином "ядро" называют символическое представление группы элементов. Алгоритм классификации заключается в эвристическом выделении нескольких исходных ядер, группировании путем присоединения к наиболее близкому ядру остальных элементов и вычислении новых ядер. Если новое разделение и его ядра на следующем шаге остаются неизменными, процесс прекращается, а получившееся разделение считается окончательным. Процедура группирования показана на рисунке:
![]()

а) б) в) г) д)
Рисунок 12.7 – Этапы группировки методом динамических ядер: а) – множество исходных объектов; б) – выбраны ядра для начальной группировки; в) – множество объектов разделяется на два класса по близости к ядрам; г) – вычисляются новые ядра;
д) – процедура повторяется
Применим вышеописанную модель типологических характеристик географических объектов для классификации административных районов по комплексу интегральных показателей, влияющих на здоровье населения по данным ГИС «Здоровье населения Красноярского края» (таблица 12.1).
Связи территориальных единиц по комплексу показателей могут быть наглядно представлены в виде дендрита – древовидного неориентированного графа (рисунок 12.8). На верхнем уровне иерархического разбиения выделяются северные районы края – Енисейский, Туруханский, Казачинский и город Игарка, что объясняется суровостью погодных условий и низким уровнем социально-экономического развития.
В разбиении оставшихся районов основное значение имеют средневзвешенный коэффициент токсичности выбрасываемых веществ, индексы ресурсов здравоохранения и эффективности их деятельности. В этой ветви дерева выделяются два класса. В первый класс (уровень 011) входят районы с большими значениями индексов антропогенной нагрузки по приведенному валовому выбросу и токсичности выбрасываемых веществ. Это районы, примыкающие к промышленным центрам, транспортным магистралям. Второй класс (уровень 012) включает районы центральной части Красноярского края с умеренным климатом и преимущественно сельской занятостью населения. Дальнейшее разбиение классов 011 и 012 выделяет районы с высоким уровнем социально-экономического развития, развитыми и эффективными ресурсами здравоохранения.
Построенная на основе дендрита тематическая карта показана на рисунке 12.9. Заметим, что районы, принадлежащие одному иерархическому уровню, сгруппированы и на карте. Особенно хорошо выделяются северные районы (уровень 02) и восточные районы (уровень 0112), группировка которых обусловлена климатическими факторами. В центральной части края вокруг расположены сельскохозяйственные районы (уровень 0122). Особо выделяются Новоселовский, Шарыповский и Ужурский районы, условия жизни населения которых более схожи с Кемеровской областью.
Таблица 12.1
|
№ |
Район |
ИСЭР |
СП января |
СП июля |
СКТВ |
РЗ |
ЭДЗ |
ИАНПВВ |
|
1 |
Абанский |
33,6 |
2,95 |
-0,24 |
5,60 |
0,63 |
0,86 |
0,097 |
|
2 |
Ачинский |
35,7 |
3,13 |
-0,24 |
17,16 |
1,08 |
0,50 |
11,96 |
|
3 |
Балахтинский |
38,5 |
2,74 |
-0,23 |
8,58 |
0,82 |
0,76 |
0,356 |
|
4 |
Березовский |
35,7 |
2,74 |
-0,22 |
6,20 |
0,53 |
0,76 |
0,329 |
|
5 |
Бирилюсский |
34 |
2,73 |
-0,21 |
7,22 |
0,74 |
1,09 |
0,119 |
|
6 |
Боготольский |
33,8 |
2,73 |
-0,21 |
8,17 |
0,77 |
0,69 |
0,449 |
|
7 |
Богучанский |
34,2 |
3,02 |
-0,24 |
7,26 |
0,86 |
0,46 |
0,88 |
|
8 |
Большемуртинский |
33,9 |
2,95 |
-0,24 |
4,38 |
0,76 |
0,73 |
0,12 |
|
9 |
Большеулуйский |
35,5 |
3,13 |
-0,24 |
13,79 |
0,69 |
0,97 |
28,712 |
|
10 |
Дзержинский |
34,7 |
2,95 |
-0,24 |
1,70 |
0,63 |
0,69 |
0,0385 |
|
11 |
Емельяновский |
37,4 |
2,74 |
-0,24 |
13,36 |
0,43 |
0,95 |
1,667 |
|
12 |
Енисейский |
32,5 |
2,9 |
-0,2 |
6,60 |
0,88 |
0,38 |
0,595 |
|
13 |
Ермаковский |
33,6 |
2,53 |
-0,3 |
5,25 |
0,58 |
0,58 |
0,041 |
|
14 |
Идринский |
33,7 |
2,62 |
-0,25 |
4,82 |
0,69 |
0,55 |
0,048 |
|
15 |
Иланский |
33,9 |
3,24 |
-0,3 |
8,63 |
0,68 |
0,77 |
0,41 |
|
16 |
Ирбейский |
34,1 |
2,41 |
-0,14 |
6,08 |
0,77 |
0,35 |
0,042 |
|
17 |
Казачинский |
32,6 |
2,9 |
-0,2 |
7,73 |
0,82 |
0,59 |
0,369 |
|
18 |
Канский |
34,4 |
3,24 |
-0,3 |
7,73 |
0,96 |
0,24 |
0,745 |
|
19 |
Каратузский |
33,8 |
2,53 |
-0,3 |
6,68 |
0,84 |
0,41 |
0,146 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
36 |
Тасеевский |
33,4 |
3,09 |
-0,23 |
5,35 |
0,74 |
0,43 |
0,346 |
|
37 |
Туруханский |
33 |
4,7 |
0,14 |
10,67 |
0,96 |
0,56 |
2,669 |
|
38 |
Тюхтетский |
33,8 |
2,73 |
-0,21 |
0,00 |
0,94 |
0,47 |
0 |
|
39 |
Ужурский |
35,6 |
2,66 |
-0,18 |
11,21 |
0,55 |
0,71 |
0,873 |
|
40 |
Уярский |
34,9 |
3,24 |
-0,3 |
7,58 |
1 |
0,54 |
0,401 |
|
41 |
Шарыповский |
36,3 |
2,66 |
-0,18 |
21,84 |
0,86 |
0,44 |
7,348 |
|
42 |
Шушенский |
33,8 |
2,53 |
-0,3 |
7,57 |
0,91 |
0,33 |
0,239 |
Прим.: ИСЭР – индекс социально-экономического развития; СП – суровость погоды, СКТВ – средневзвешенный коэффициент токсичности выбрасываемых веществ; РЗ – ресурсы здравоохранения; ЭДЗ – эффективность здравоохранения; ИАНПВВ – индекс антропогенной нагрузки.

Рисунок 12.8 – Классификация административных районов по комплексу факторов, влияющих на здоровье населения

Рисунок 12.9 – Картографическое изображение классификации районов
Влияние географических явлений друг на друга может быть выявлено путем анализа их взаимного территориального расположения при помощи сопоставления их изображений на географических картах. Существует множество алгоритмов, позволяющих выявлять не только ярко выраженные, но и скрытые, осложненные рядом факторов взаимосвязи. Большая часть этих алгоритмов основана на вычислении парных коэффициентов корреляции по дискретным территориальным ячейкам. Для оценки степени соответствия формы контуров объектов двух площадных слоев можно использовать информационные модели: полихорические показатели связи и карты энтропии контуров. Взаимосвязи в пространственном расположении явлений можно выявить также путем расчета коэффициентов соответствия площадей. Сила взаимосвязи оценивается при помощи 2 - статистики.
Для простой оценки взаимосвязи между географическими явлениями можно вычислять коэффициент соответствия площадей KCAC (CAC – Coefficient of Areal Correspondence) – отношение площади пересечения двух регионов к площади объединения этих регионов (рисунок 13.1). Вычисление коэффициента KCAC в ГИС осуществляется при помощи оверлейных операций. Два явления изображаются в одинаковом масштабе, и контуры одного явления накладываются на контуры другого. Если между картографическими объектами нет пространственного соответствия, коэффициент KCAC=0, а в случае полного совпадения границ объектов коэффициент KCAC=1:
Площадь(C)
KCAC ![]() (13.1)
(13.1)
Площадь(A) Площадь(B) Площадь(C)
![]()



KCAC ![]()
0; KCAC
0; KCAC ![]()
0,25; KCAC
0,25; KCAC ![]() 1;
1;
B C A
Рисунок 13.1 – Коэффициент соответствия площадей
Коэффициент соответствия площадей обеспечивает простую оценку пространственной связи между географическими явлениями, но не дает информации о статистической значимости этой связи. Этого недостатка лишена матрица сходства, введенная в 1970г. Коуртом и получаемая по формуле
Площадьсовпадение(i, j)Площадьнесовпадение(i, j)
MRi, j ![]() . (13.2)
. (13.2)
Площадьобщая(i, j)
Область значений элемента матрицы MRi,j, представляющего степень взаимосвязи i-го и j-го контура, лежит от –1 (полная взаимосвязь) до +1 (полная положительная взаимосвязь). Значение элемента матрицы MRi,j=0 показывает отсутствие взаимосвязи. Распределение в этом случае считают нормальным и используют тесты статистической значимости.
Рассмотрим следующую практическую задачу. На некоторую территорию имеются одномасштабные карты среднегодового количества осадков и урожайности пшеницы (рисунок 13.2). Требуется оценить взаимосвязь между количеством выпадающих осадков и урожайностью; сравнивая распределение явлений на картах, можно лучше понять взаимосвязь между явлениями.

Рисунок 13.2 – Преобразование карты в растр и наложение слоев
В примере на рисунке 13.2 на карты количества осадков и урожайности наложена регулярная сеть и получены растровые слои в ГИС. Чтобы получить более точную характеристику взаимосвязи, нужно уменьшить размер растровой ячейки. На исходных картах показаны по два значения для каждого слоя (высокая и низкая урожайность; большое и малое количество осадков). Поэтому на оверлее полученых растров возможны 4 варианта пар количество осадков – урожайность. Запишем число встречаемости каждой пары значений в таблице частот Oi,j, i=1..n, j=1..m и создадим таблицу ожидаемых частот Ei,j .
Урожайность Ei,j
n m
Or, j *Oi,s
Ei, j ![]() r1 n m s1
r1 n m s1
Oq,p
q 1 p 1
|
4 ,6 |
|
|
|
|
|
Oi,j |
Выс. |
Низ. |
|
Много |
8 |
2 |
|
Мало |
5 |
13 |
![]() Наблюдаемые частоты
Наблюдаемые частоты
Ожидаемые частоты
Рисунок 13.3 – Таблицы наблюдаемых и ожидаемых частот
Вычислим показатель 2 по формуле
2 n m (Oi, j Ei, j )2
![]() Oi, j .
(13.3)
Oi, j .
(13.3)
i 1 j 1
Большие значения 2 индицирует отсутствие взаимосвязи, большие значения 2 указывают на сильную взаимосвязь между географическими явлениями. Чтобы определить, является ли связь статистичеки значимой, используют специальные таблицы.
Для оценки взаимосвязи между географическими объектами используют также коэффициент ассоциации Юла Q, изменяющийся от –1 до 1 :
O1,1 *O2,2 O1,2 *O2,1
Q ![]() .
(13.4)
.
(13.4)
O1,1 *O2,2 O1,2 *O2,1 В нашем примере
2 (85)2 (25)2 (58)2 (1310)2
![]()
5,625;
5,625;

Видим, что между урожайностью пшеницы и количеством выпадающих осадков существует достаточно сильная взаимосвязь.
Чтобы обнаружить взаимосвязи между географическими явлениями через степень соответствия формы границ представляющих их регионов, можно использовать модели, основанные на информационных показателях связи и позволяющие строить карты энтропии контуров.
На карты, отражающие сравниваемые явления, накладывается регулярная сеть, шаг которой определяется детальностью карты, и создается два растровых слоя в ГИС. Построим таблицу сопряженности F (рисунок 4), в которой Fi,j – количество точек решетки, попадающих внутрь каждого контура на оверлее слоев, i – площадной объект слоя , j – объект слоя . Количество строк в таблице F обозначим N, число строк и столбцов таблицы – соответственно kb и ka. По каждой строке j и по каждому столбцу i матрицы F подсчитываются частоты точек n(b)j и n(a)i по градациям легенды карты для слоев и .
Слой Слой Оверлей

Рисунок 13.4 – Растеризация и оверлей карт, расчет таблицы сопряженности
Если между явлениями, изображенными на слоях и , существует прямая или обратная функциональная связь, все частоты в таблице сопряженности F будут сконцентрированы одной из диагоналей таблицы. По таблице сопряженности вычисляется полихорический показатель связи между явлениями, используя формулу:
![]()
S 1(ka 1)(kb 1)N1 , S ka 1 kb Fj2,i .
(13.6)
S 1(ka 1)(kb 1)N1 , S ka 1 kb Fj2,i .
(13.6)
![]()
(ka 1)(kb 1) i1 nai j1 nbj
1 42 32 1 22 72
В нашем примере S 7 6 10 9 6 10 =1.128, а показатель =0.256.
Пространственное распределение информационных показателей взаимосвязи явлений может быть показано в виде карты энтропии контуров одного явления относительно другого явления путем определения похожести контуров на сравниваемых картах. Пусть некоторый контур Aj, лежащий на карте , пересекает n контуров Bi на карте . Определим i – доли площадей пересечения Aj с каждым из контуров Bi и вычислим энтропию контура Аj :
n S(Aj Bi )
E(Aj )
i log2i ; i
![]() n ,
(13.7) i1 S(Aj Bk )
n ,
(13.7) i1 S(Aj Bk )
k1
где S(Aj Bi )– площадь пересечения контуров Aj и Bi .

Рисунок 13.5 – Расчет энтропии контуров
При вычислении энтропии контура на одном растровом слое относительно контуров на другом растровом слое S(Aj Bi )соответствует количеству узлов растровой решетки, лежащих одновременно внутри Aj и Bi. Вычислим энтропии контуров для карты заболеваемости относительно выбросов в атмосферу (рисунок 13.5). Если один контур полностью лежит внутри другого, =1, E= log2=0. Поэтому энтропия контура А2, полностью лежащего внутри контура B3, равна нулю. Определим энтропии оставшихся контуров и запишем результаты в таблице 1.
Таблица 13.1
|
|
B1 |
B2 |
B3 |
S(Aj Bi ) i |
1 |
2 |
3 |
E(Aj) |
|
А1 |
12 |
2 |
112 |
126 |
0,0952 |
0,0159 |
0,8889 |
0,569 |
|
А2 |
0 |
0 |
6 |
6 |
0 |
0 |
1 |
0 |
|
А3 |
47 |
0 |
13 |
60 |
0,7833 |
0 |
0,2167 |
0,754 |
|
А4 |
0 |
6 |
6 |
12 |
0 |
0,5 |
0,5 |
1 |
Для выявления взаимосвязей между пространственными и содержательными характеристиками географических явлений часто используют корреляционные модели: вычисляют парные коэффициенты корреляции, частные и множественные показатели связи.
Между случайными переменными X и Y существует корреляционная зависимость, если каждому значению независимой переменной X соответствует некоторое распределение переменной Y, причем с изменением значений
![]()
xi закономерно изменяются математические ожидания yi этих распределений. По тесноте различают связь сильную, среднюю и слабую, по характеру – прямую и обратную, по форме – линейную и нелинейную (рисунок 6).

)
Рисунок 13.6 – Графическое представление корреляционных зависимостей: а) – сильная прямая; б) – сильная обратная; в) – средняя прямая; г) – слабая
обратная; д) и е) – связь отсутствует; ж) и з) – нелинейная
Для аналитического изучения корреляционной зависимости между переменными x и y вычисляются коэффициенты корреляции. Если данные представлены в интервальной шкале измерений, подчиняются нормальному закону распределения и предполагается линейная корреляционная между ними, используют парный параметрический коэффициент корреляции Пирсона rxy :
n
![]() 1 i1 (xi x)(yi y)
1 i1 (xi x)(yi y)
rxy . (13.8) n nxy
Показатель корреляции рангов Спирмена rs часто используется в задачах, когда требуется оценить тесноту зависимости между признаками, не поддающимися количественному описанию. Если пронумеровать объекты, упорядоченные по какому-либо признаку, то такая совокупность объектов будет называться ранжированной. Если n – количество измерений каждой переменной, di – разница в рангах для каждой пары измерений, показатель корреляции рангов вычисляется по формуле
![]() n 23 rs 16di(n n) . (13.9)
n 23 rs 16di(n n) . (13.9)
i1
Коэффициент корреляции Спирмена является непараметрическим показателем. Его можно использовать даже без проверки гипотезы о нормальном распределении переменных и когда связь между переменными нелинейная. В качестве примера определим, существует ли взаимосвязь между количеством выпавших осадков и стоком реки. Исходные данные представлены в первом и втором столбцах таблицы 13.2.
Таблица 13.2
|
Количество выпавших осадков |
Сток реки |
d=Ранг(X)–Ранг(Y) |
d2 |
||
|
X, мм |
Ранг(Х) |
Y, тыс. м3 |
Ранг(Y) |
||
|
1,2 |
4 |
2,7 |
6 |
–2 |
4 |
|
1,8 |
5 |
2,4 |
4 |
1 |
1 |
|
4 |
10 |
8,1 |
10 |
0 |
0 |
|
3,6 |
9 |
7,2 |
9 |
0 |
0 |
|
1,9 |
6 |
2,5 |
5 |
1 |
1 |
|
2,4 |
7 |
3,7 |
7 |
0 |
0 |
|
2,7 |
8 |
4,6 |
8 |
0 |
0 |
|
0,4 |
2 |
1,7 |
2 |
0 |
0 |
|
0,1 |
1 |
1,8 |
3 |
–2 |
4 |
|
0,9 |
3 |
1,4 |
1 |
2 |
4 |
Предположим, данные не подходят для того, чтобы использовать парный коэффициент корреляции (например, не соответствуют нормальному распределению), и мы вынуждены использовать показатель корреляции рангов. Ранжируем оба ряда исходных данных возрастанию и вычислим rs:
rs 1 63 d2 1 ![]() 6314 10,085 0,915 n n 10 10
6314 10,085 0,915 n n 10 10

Рисунок 13.7 – Схема построения карты связи явлений в виде изокоррелят
Подробную картину пространственного варьирования взаимосвязей между явлениями можно получить, изображая показатели связи в виде изокоррелят. Для этого на сравниваемые карты строго скоординировано накладывается регулярная сетка точек, используемых для вычисления показателей связи при помощи «скользящего окна». В примере на рисунке 13.7 используется окно 3x3. На каждой карте попадающие внутрь окна ячейки преобразуются в ряды. Порядок развертки растровых ячеек при этом роли не играет – требуется только, чтобы на всех картах правила развертки были одинаковыми. По полученным рядам для каждой контрольной точки вычисляются коэффициенты корреляции, которые затем изображаются на карте в виде изокоррелят.
В картографическом моделировании наиболее сложны и трудно формализуемы модели пространственного распространения географических явлений. Для моделей структуры и взаимосвязей явлений большая часть операций может быть выполнена при помощи встроенных в ГИС функций. Конструирование моделей динамики явлений выполняется обычно на уровне ГИСприложений. Сложности существуют также при визуализации моделей динамики: изобразительных средств для показа распространения явления по территории в картографии имеется не так много, как для моделей других типов.
Для изучения закономерностей распространения явления по территории карты часто используется метод Монте-Карло. В таком случае явление рассматривается как некоторая абстрактная система, элементы которой могут находиться в нескольких состояниях. Для того чтобы определить элементы этой системы, изображенная на карте площадь разбивается на мелкие территориальные единицы. Разбиение может быть регулярным (здесь возможно использовать растровую модель данных ГИС) или нерегулярным.
Вероятность пребывания элемента в каком-либо состоянии подчиняется определенному закону распределения, характеризующему саму систему и связи между ее различными состояниями. Конкретные состояния системы генерируются при помощи датчиков псевдослучайных чисел. Выполнив эксперимент достаточно большое число раз и обработав полученные данные статистическими методами, получают численные показатели направления и скорости распространения явления.
В качестве примера использования метода Монте-Карло для моделирования динамики явлений рассмотрим модель распространения эпидемии по методике В.С. Тикунова. Имеется карта населенных пунктов в виде точек с характеристиками численности населения. Наложим на нее регулярную сеть и получим разбиение площади карты на n клеток. Для каждой ячейки сети при помощи оверлейной операции в ГИС легко определить dj – численность населения, проживающего на соответствующей этой ячейке территории. Координаты ячейки обозначим (xj,yj), j=1..n.
Ячейки полученного разбиения могут находиться в одном из трех состояний: “1” – эпидемия еще не начиналась, “2” – территория охвачена эпидемией, “3” – эпидемия закончилась. Возможны два перехода между состояниями системы: из состояния “1” в “2” и из состояния “2” в “3”. Ячейки изменяют свое состояние только через дискретные промежутки времени Δt=ti+1–ti. В начальный момент времени t0 по крайней мере одна ячейка охвачена эпидемией и находится в состоянии “2”. Если в j-й территориальной единице в какой-то момент времени ti начинается эпидемия, ячейка переходит из состояния “1” в состояние “2”. Длительность эпидемии пропорциональна численности населения в ячейке: Δtj=K · dj ,где К – некоторая постоянная величина для всей территории карты, выбираемая эмпирически. Эпидемия заканчивается и территория переходит в состояние “3”, когда истечет время Δtj.
|
|
|
|||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
Эпидемии еще не было
Охвачена эпидемией
Эпидемия закончилась
Рисунок 14.1 – Исходная матрица для моделирования распространения эпидемии
Вероятность pj возникновения эпидемии в момент времени ti больше нуля только в ячейках, находящихся в состоянии “1” (в состояние “2” можно перейти только из состояния “1”). Вероятность pj пропорциональна сумме
p j ~p j ![]() d j 2dLk
, (14.1) m
d j 2dLk
, (14.1) m
R
k1 j,Lk
где dj – численность населения в j-ой ячейке, dLk – численность населения в
Lk-ой ячейке, пребывающей в момент ti-1 в состоянии “2”, а R2j,Lk – квадрат расстояния между j-ой и Lk-ой ячейками.
m
Вычислим сумму ~p j и определим вероятности возникновения
j1
эпидемии в ячейках по формуле pj ~pj 1. Видим, что p j 1. Найдем
j
суммы Bj pk , где B0=0 и j=1..n. Для выбора ячейки, в которая на сле-
k1
дующем шаге перейдет в состояние “2”, сгенерируем датчиком псевдослучайных чисел переменную ξ, принимающую значения от 0 до 1. Выберем j-ю ячейку, для которой выполняется условие Bj1 Bj . Так на каждом шаге одна ячейка переходит в состояние “2”. Можно также непосредственно использовать pj для моделирования перехода ячейки с состояние эпидемии. Для этого сгенерируем для каждой ячейки случайную величину ξj , и если ξj pj , то ячейка переходит в состояние «2». В этом случае на каждом шаге в состояние “2” может перейти 0, 1 или несколько ячеек. Момент времени, когда
~
ячейка перешла в состояние “2”, запоминается в переменной tj . Ячейка на~ ходится в состоянии эпидемии в течение времени Δtj. Как только t j tj ti , ячейка переводится в состояние “3”.
Процесс моделирования можно прекратить после выполнения определенного числа циклов в момент ti, i=1,2,3…n , или если больше не осталось ячеек в состоянии “1”. На рисунке 14.2 изображены значения ячеек в различные моменты времени (с шагом 5). Здесь уже просматриваются некоторые закономерности распространения явления по территории карты. Однако при этом нужно помнить, что на рисунке мы видим результат, сгенерированный датчиком случайных чисел. Строить по нему достоверные объяснения характера распространения эпидемии по территории еще нельзя.

Рисунок 14.2 – Состояние ячеек для различных моментов времени ti
Повторим процесс моделирования m раз с одинаковыми исходными данными; в итоге для каждой j-той территориальной единицы получим выборку ~tj1, ~tj2,L~tjm , по которой можно получить статистические оценки случайной величине – времени начала эпидемии (рисунок 14.3-а). По полученной регулярной сетке можно построить карту в виде изолиний для ожидаемого времени начала эпидемии.
|
14 |
9 |
12 |
21 |
18 |
27 |
|
16 |
5 |
14 |
15 |
15 |
24 |
|
9 |
0 |
5 |
10 |
20 |
23 |
|
12 |
7 |
11 |
15 |
22 |
20 |
|
18 |
13 |
14 |
20 |
23 |
27 |
 б)
б)
а) 0 1 2 3 4 5
Рисунок 14.3 – Распространение эпидемии по территории:
а) – математические ожидания M~tj ; б) – карта в изолиниях
"Гравитационные" модели распространения явления по территории используются в тех случаях, когда развитие явлений трудно выразить при помощи математических уравнений. При помощи этих моделей исследуются потоки миграционные потоки населения и его категорий, объем потоков грузов и пассажиров, количество телефонных разговоров между населенными пунктами и т.п. "Гравитационные" модели основываются на формуле взаимодействия населенных пунктов Стьюарта, созданной по аналогии с моделью тяготения Ньютона. Предполагается, что интенсивность взаимодействия между двумя городами прямо пропорциональна их людности p1 и p2 и обратно пропорциональна квадрату расстояния между ними:
p1 p2
F ![]() 2 2
. (14.2)
2 2
. (14.2)
x1 x2 y1 y2
В качестве примера построим модель распространения абстрактной эпидемии по территории, используя методику Тикунова для расчета этапности развития эпидемии и картографирования ее распространения. Возьмем карту населенных пунктов окрестностей г. Красноярска с характеристикой численности проживающего в них населения. Для объяснения методики возьмем города с численностью жителей более 50000 человек; численность населения в них и их координаты приведены в таблице 14.1.
Таблица 14.1
|
№ п/п |
Город |
Население, чел. |
X, долгота |
Y, широта |
|
1 |
Красноярск |
873900 |
92,9062 |
56,0029 |
|
2 |
Ачинск |
123200 |
90,4856 |
56,2671 |
|
3 |
Канск |
107700 |
95,7076 |
56,2003 |
|
4 |
Лесосибирск |
69500 |
92,4779 |
58,2378 |
|
5 |
Назарово |
64400 |
90,3992 |
56,0217 |
По формуле 14.1 вычислим расстояния для каждой пары населенных пунктов и запишем результат в таблице 14.2. Зададим номер пункта, из которого начинается распространение эпидемии, например, г. Канск. Выберем из этой строки максимальный элемент, показывающий наибольшее взаимодействие Канска с Красноярском. Естественно предположить, что в первую очередь эпидемия распространится в Красноярск.
Таблица 14.2
|
|
Красноярск |
Ачинск |
Канск |
Лесосибирск |
Назарово |
|
Красноярск |
|
4.578 |
3.048 |
0.970 |
2.301 |
|
Ачинск |
4.578 |
|
0.126 |
0.137 |
10.225 |
|
Канск |
3.048 |
0.126 |
|
0.084 |
0.063 |
|
Лесосибирск |
0.970 |
0.137 |
0.084 |
|
0.058 |
|
Назарово |
2.301 |
10.225 |
0.063 |
0.058 |
|
На следующем шаге максимальный элемент нужно искать уже по двум строкам: по Канску и Красноярску, ведь эпидемия может распространиться далее из любого из этих городов. Заметим также, что при выборе максимального элементы столбцы, соответствующие городам, охваченным эпидемией, следует пропускать. Этапность распространения эпидемии можно показать на карте стрелками различной толщины (рисунок 14.4). На рисунке 14.5 показана карта этапности распространения эпидемии, построенная по 47 населенным пунктам центральной части Красноярского края.
![]() Красноярск
Красноярск
Красноярск
Красноярск
Рисунок 14.4 – «Гравитационная» модель распространения эпидемии:
a) – начальная точка в Канске; б) – в Лесосибирске

Рисунок 14.5 – Этапность распространения эпидемии при логарифмированных показателях людности населенных пунктов
Геоинформационные системы обеспечивают множество разнообразных операций обработки цифровых карт, данных дистанционного зондирования, моделей рельефа и др. Однако невозможно предусмотреть все функции работы с пространственными данными, необходимые для “тонкой настройки” системы под конкретную задачу. В ГИС первоначально эту проблему решали путем включения в пакет как можно большего количества функций. Современные системы используют другой подход – к ограниченному числу команд обработки пространственной информации, хорошо специфицированных и оптимизированных по скорости доступа и обработки геоданных, добавляют языковые средства, позволяющие создавать пользовательские приложения и тем самым приспосабливать ГИС к конкретным производственным условиям.
Средства создания приложений используются для расширения функциональных возможностей ГИС. Если существует возможность доступа к пространственным данным из программы, можно создавать любые дополнительные функции работы с этими данными. Для многих ГИС имеются свободные и коммерческие библиотеки таких дополнительных функций, приспосабливающие ГИС к практическим задачам.
Пользователями ГИС как средства автоматизированного принятия управленческих решений на основе геоданных часто являются специалисты, далекие не только от геоинформатики, но и вообще от информационных технологий. Поэтому разработчики ГИС-продуктов должны обеспечивать возможность максимально простого, не требующего специальных знаний режима работы пользователя с пространственной информацией.
Языки создания приложений также используются в ГИС для определения заданий. При работе с большим количеством однотипных слоев часто выполняется одна и та же последовательность операций обработки. Основная трудоемкость и затраты времени здесь ложатся на взаимодействие оператора с интерфейсом ГИС. Кроме того, такая однообразная, механическая работа приводит к снижению внимания оператора и возникновению ошибок. Чтобы автоматизировать труд оператора, создается программа-задание, полностью повторяющая действия оператора при работе с ГИС.
В современном программном обеспечении ГИС большая часть систем включает средства для решения поставленных выше задач. В ГИС Arcview используется язык создания приложений Avenue, в ГИС MapInfo – MapBasic, в ERDAS для создания скриптов имеется макроязык EML, в GRASS задания формируются на языке командной оболочки shell и т.д.
Язык MapBasic используется в среде программирования ГИС MapInfo и содержит более 300 операторов и функций для работы с пространственными данными. Как язык программирования MapBasic характеризуется модульной структурой программы, организацией циклов, возможностями управления процессами, построения обработчиков ошибок и откликов на события. В программах на MapBasic можно использовать вызовы к библиотекам DLL, организовывать взаимодействие с другими Windows-приложениями через DDE, обращаться к удаленным базам данных при помощи ODBC.
Для доступа к данным используется стандартный язык запросов SQL, возможности которого расширены пространственными запросами: вычислением длин и площадей, определением вложенности, соседства и пересечения объектов. Язык MapBasic позволяет создавать и модифицировать географические объекты (точечные, линейные, площадные объекты, текстовые подписи, буферные зоны и др.), модифицировать стили изображения картографических объектов. Также имеются средства для оверлея полигонов, включающие функции объединения, разрезания, удаление внешней и перекрывающей части объекта.
При помощи MapBasic формировать карты из отдельных слоев, создавать тематические карты и легенды к ним, выполнять поиск и геокодирование объектов, выполнять проекционные преобразования. В среде MapInfo язык MapBasic позволяет разрабатывать собственные меню, панели инструментов и диалоги, упрощающие работу конечного пользователя с ГИС и позволяющие решать практические задачи организации.
Язык Avenue – объектно-ориентированный язык программирования, использующийся в ГИС ArcView для создания приложений и “тонкой настройки” ГИС под конкретную задачу. Для ГИС ArcView на этом языке создано множество модулей обработки геоданных: Spatial Analyst – для пространственного анализа данных в растровом формате, 3D Analyst – для пространственного анализа триангуляционной нерегулярной сети, Geostatistical Analyst – для комплексного статистического анализа растровых данных, Network Analyst – для поиска оптимальных путей, построения зон обслуживания.
Существует также множество сторонних программных инструментов для создания ГИС-приложений, не связанных с разработчиками коммерческих ГИС. Многие из этих инструментов доступны на сайте www.freegis.org. Разработка программного обеспечения ГИС в свободном сегменте ведется чаще всего на языках Си, Java, Perl, TCL, Python. Для доступа к пространственным данным из приложений, разрабатываемых на различных языках программирования, используются интерфейсы API к файлам данных ГИС, библиотеки для преобразования форматов файлов и картографических проекций.
Приведем для примера описание наиболее популярных библиотек.
Библиотека LIBTIFF обеспечивает стандартный программный интерфейс Си чтения и записи информации в формате TIFF. Для работы с географическими тегами в этом формате существует надстройка – LIBGEOTIFF. Есть свободные библиотеки для работы с изображениями и в других растровых форматах – libjpg, libpng, gd и многие другие.
Если для растровых изображений общим форматом для большинства ГИС можно считать TIFF, в случае с векторными данными для каждой системы требуется свой API. Библиотека С++ MITAB, основанная на OGR и спецификации консорциума OpenGIS (OGC), используется для чтения и записи бинарных файлов ГИС MapInfo, а также файлов формата MIF/MID. Библиотека SHAPELIB предназначена для работы с shape-файлами ESRI ArcView и может использоваться с языками Си, Perl и Python. Библиотека Си DGNLib позволяет читать векторные данные из файлов Microstation DGN, библиотека классов C++ DIME – импортировать, манипулировать и экспортировать данные в формате DXF AutoCAD. Программный интерфейс GML4J для Java предназначен для работы с GML (Geography Markup Language) – структурой данных, основанной на XML и использующейся для кодирования географической информации в соответствии с рекомендациями OGC.
Среди конверторов пространственных данных в первую очередь следует упомянуть о библиотеке GDAL (Geospatial Data Abstraction Library), позволяющей манипулировать геопространственными данными в разнообразных форматах и представляющей единую абстрактную модель данных для вызовов из пользовательского приложения. Специализированных конверторов существует несколько десятков: gen2shape, sdtd2dem, shp2svg и др.
Для расчета картографических проекций во многих ГИС используется ставшая уже фактически стандартной библиотека PROJ4. Так, в классической ГИС ArcInfo компании ESRI преобразования проекций выполняются при помощи этой библиотеки. Программа proj конвертирует географические координаты в координаты на плоскости карты (,) (x, y) и позволяет использовать почти все распространенные картографические проекции и любые геодезические даты. Программа позволяет выполнять также обратные преобразования (x, y) (,).
При самостоятельной разработке программного обеспечения ГИС могут быть полезны многочисленные библиотеки обработки цифровых карт и растровых изображений, многие из которых уходят корнями в 70-е годы прошлого века и первоначально создавались на Фортране и в настоящее время транслированы на Си. Библиотека HIPR2 (Hypermedia Image Processing Reference) содержит разнообразные функции для обработки изображений, выполняющие арифметические, геометрические, морфологические операции над растровыми слоями, выделение объектов, цифровые фильтры, преобразование изображений (Фурье, Хоха), синтез изображений. Пакет DEMTools может быть полезен для визуализации цифровых моделей рельефа и представления моделей местности в Интернет – пакет включает конвертор модели DEM в формат VRML.
Для организации взаимодействия разрабатываемого ГИС-приложения с GPS-приемником существуют разнообразные программные интерфейсы и программы. Автомобильная навигационная система GPSDrive позволяет отображать местоположение машины на масштабируемой карте. Библиотека JEEPS содержит средства коммуникации с устройствами GPS Garmin, включая NMEA, и функции обработки полученных с приемника координат и маршрутов, их картографирования в различных проекциях.
Результаты обработки географических данных, покидая ГИС, неминуемо должны трансформироваться в “человеко-читаемый” документ. К таким документам принадлежат табличные данные, получаемые при помощи SQL-запросов к пространственной базе данных, построенные на их основе графики и диаграммы, изображения, карты и 3D-модели. Вывод ГИСпродуктов в виде таблиц, графиков и изображений может выполняться на обычных офисных компьютерах и принтерах. Карты, модели рельефа и космические снимки высокого разрешения выводятся на печать при помощи специализированных крупноформатных периферийных устройств.
В программном обеспечении ГИС содержится богатый набор средств для генерации выходного продукта, а аппаратные средства включают множество периферийных устройств для его печати на бумаге или пластике. С развитием технологий Интернет широкое распространение получили системы передачи картографической информации потребителю ГИС-продуктов через WEB-интерфейс.
Развитие средств вычислительной техники постепенно стирает грань между устройствами вывода информации общего назначения и устройствами вывода информации ГИС. В 1990-е мониторами с крупным разрешением комплектовались только очень дорогие графические рабочие станции, сейчас такие мониторы устанавливаются на обычные бытовые и офисные компьютеры. Это же касается вывода карт на бумажный носитель: разрешение бытовых принтеров становится достаточным для печати космических снимков. Можно сказать, что единственным специфичным для ГИС периферийным устройством остаются только графопостроители (рисунок 16.1).
Графопостроитель или плоттер – устройство для автоматического вычерчивания с большой точностью рисунков, схем, сложных чертежей, карт и другой графической информации на бумаге, пластике или кальке.
В первых планшетных графопостроителях бумага неподвижно закреплена на плоском столе. Использовалось электростатическое, вакуумное, либо механическое закрепление. Головка или блок перьев перемещалась по двум перпендикулярным направлениям. Современные плоттеры являются в основном высокоточными струйными принтерами крупного формата, приспособленными для задач ГИС и CAD. Плоттеры позволяет печатать карты на листах крупных форматов – А0, А1, А2. Некоторые модели могут печатать на листах шириной до пяти метров. Наиболее распространены плоттеры фирм Calcomp, Hewlett-Packard, Epson, Canon и др. Стоимость плоттеров варьируется от тысяч до десятков тысяч долларов и зависит в основном от формата печатного листа.

Рисунок 16.1 – Графопостроитель Canon W6200
Связь плоттера с компьютером параллельный или SCSI-интерфейс. Некоторые модели графопостроителей оснащаются встроенным буфером объемом несколько мегабайт. Для передачи данных на печатающее устройство используются форматы PostScript, HPGL и др. Общепринятым форматом передачи карт для печати в типографии является PostScript – язык описания страниц, используемый в издательских системах.
Вывод на печать крупноформатных карт – операция дорогостоящая. Снизить себестоимость отпечатков в 1,5-2 раза позволяет система непрерывной подачи чернил, впервые реализованная в струйных плоттерах Encad. Система обеспечивает непрерывное поступление чернил в картриджи из емкостей. При этом дозаправку плоттера чернилами можно выполнять непосредственно во время печати. Большой объем емкостей (от 500 мл каждого из 4-х CMYK цветов) позволяет использовать плоттер в течение длительного времени без участия оператора, избегать брака, вызванного преждевременным окончанием чернил во время печати.
Слои, полученные путем пространственного анализа в ГИС, наложенные на векторную тематическую основу или растровый снимок и выведенные на печатающее устройство еще нельзя назвать картой. Значительная часть работ по созданию карты начинается с завершением подготовки полотна карты. Процесс создания карты включает не только математически точное описание местоположения географических феноменов и явлений, но и работу над оформлением картографических объектов в принятой системе условных знаков, графическим дизайном карты.
В программном обеспечении ГИС основные усилия прикладываются на реализацию процедур ввода данных, моделирования и пространственного анализа, а вопросы дизайна выходного картографического продукта обычно отодвинуты на второй план. Лишь немногие системы позволяют создавать правильно и красиво оформленные карты.
При проектировании карты разрабатывается макет ее компоновки, определяющий положение изображаемой на карте территории относительно рамок карты размещение названия карты, ее легенды, дополнительных картврезок, графиков, схемы разграфки карты. Рамкой карты является система линий, окаймляющей изображение карты. Внутренняя рамка ограничивает картографическое изображение, и на нее наносятся линейные величины градусов и минут. Рамка содержит подписи наиболее значимого населенного пункта, год съемки и издания карты, линейный и численный масштаб, номенклатуры смежных листов и т.д. Внешняя рамка, окаймляющая все внутренние рамки карты, является декоративной.
Зарамочное оформление карты включает элементы, нарисовать которые стандартными средствами большинства ГИС невозможно. Для правильного построения элементов зарамочного оформления используют шаблоны и дополнительные программы. Одним из вариантов решения проблемы является передача подготовленного в ГИС картографического изображения в графический редактор общего назначения или издательскую систему.
Создание подписей географических объектов на карте – важная проблема автоматизированной цифровой картографии. Она заключается в позиционировании текстовых подписей на карте со следующими условиями: подписи должны разборчиво для читателя соотноситься с пространственными объектами, не должны перекрываться, закрывать другие важные элементы карты. В традиционной картографии эта задача по некоторым оценкам занимает до 20% времени подготовки карты, следовательно, создание автоматических процедур размещения подписей является важной задачей.
Проблема размещения подписей на карте разбивается на подзадачи в соответствии с размерностью подписываемых объектов (полигоны, линии и точки). Создание подписей для точечных объектов заключается в следующем. Задано множество отдельно расположенных точек и множество подписей, соответствующих этим точкам. Требуется расположить подписи так, чтобы минимизировать число пересечений меток между собой и с точками.
Для решения этой задачи подписи моделируются прямоугольниками переменного размера, точка привязки которых может находиться в одном уз углов прямоугольника или в одной из средних точек его сторон. Тогда для каждой точки возможны восемь вариантов размещения подписи, а на карте, содержащей n точек возможны 8n вариантов. Непосредственный перебор всех вариантов размещения, очевидно, невозможен. Однако на практике полный перебор и не требуется: подписываемые объекты на реальной карте разнесены по территории и пересекаются друг с другом не часто. Если для карты построен пространственный индекс, простой рекурсивный алгоритм обхода дерева позволяет быстро найти решение.
Развитие вычислительной техники привело к появлению Internet – наиболее разветвленной и стремительно развивающейся глобальной компьютерной сети, получившей в последнее время широкое распространение как универсальное средство передачи коммерческой, научной и учебной информации. В области геоинформатики возможности Internet могут применяться для решения такой актуальной проблемы, как обеспечение связи поставщиков и потребителей геоинформационных ресурсов, в том числе для организации доступа пользователей к цифровым картам.
В настоящее время сеть Internet широко используется в задачах ГИС. Существуют разнообразные технические средства для представления геоинформационных моделей в Internet. Язык разметки гипертекстовых страниц HTML предоставляет базовые средства для создания WEB-страниц. В HTML-странцу могут быть внедрены server-side CGI скрипты и client-side JavaScript. Для повышения функциональных возможностей WEB-страниц также могут использоваться программы на языке Java, компоненты ActiveX.
Современные разработки, связанные с появлением функциональных возможностей ГИС в Интернет, называются WebGIS. При помощи WebGIS распределенная геоинформация становится доступной широкой аудитории по всему миру. Пользователи WebGIS получают доступ к приложениям ГИС через WEB-браузер без покупки специального программного обеспечения.
Производители коммерческого программного обеспечения включают в свои системы модули WEB-картографии. Компания ESRI создает для публикации геоданных в Интернет картографический сервер ArcIMS, Mapinfo Corporation – сервер MapInfo MapXtreme для Windows и в Java-редакции. В секторе свободного программного обеспечения усилия по разработке WebGIS координируются консорциумом Open GIS. Лицензионные соглашения этих программ позволяют свободно использовать их в некоммерческих приложениях, модифицировать исходные тексты программ, что обеспечивает простоту их адаптации для конкретной задачи. На сайте www.opengis.org представлены несколько десятков свободных WebGIS. Среди пользователей наиболее популярны системы UMN MapServer, Geoserver – реализация на Java спецификаций OGC, MapIT! – сервер для публикации растровых карт, degree, Practical Map Server, GeoTools и др.
Картографический сервер UMN MapServer разработан в университете штата Миннесота. ГИС MapServer распространяется в виде исходных текстов, что обуславливает их хорошую переносимость. Программное обеспечение Mapserver представляет собой встраиваемое в поток CGI приложение, которое на основе файла описания карты и набора географических данных строит картографическое изображение. Пользователь получает результат в виде HTMLстранцы, в которую встроено созданное изображение и элементы интерфейса, позволяющие перемещать фокус изображения, изменять масштаб, обращаться к атрибутным таблицам картографических слоев (рисунок 16.2).

При обращении пользователя к MapServer браузер отправляет запрос на получение карты. Сервер HTTP принимает запрос и запускает CGIприложение – программу генерации изображения (рисунок 16.3). Эта программа открывает файл описания карты и выполняет его синтаксический разбор. В результате программа генерации изображения получает все необходимые для работы параметры. Созданное растровое изображение в формате GIF или PNG помещается в каталог временных файлов, доступный через HTTP.

Конфигурация цифровой карты в MapServer настраивается в файле описания карты, где определяется структура генерируемого картографического изображения, цвета, символы и шаблоны закраски объектов, взаимодействие с HTTP-сервером. Файл описания карты записывается в текстовом формате информационных объектов, из которых формируется карта. Иерархия объектов карты показана на рисунок 16.4. Этими объектами являются картографические слои, тематические классы, подписи объектов, стили точек, линий и полигонов, а также WEB-интерфейс, оформленный в виде HTML-шаблона.
На верхнем уровне иерархии находится объект Map, в котором указываются общие параметры картографического изображения: экстент карты, пути к файлам данных, размер формируемого изображения и т.п. Объекты, перечисленные в предыдущем абзаце, являются потомками объекта Map.

Рисунок 16.4 – Иерархия объектов в файле описания карты
В соответствии с общепринятой организацией данных в ГИС, в MapServer картографическое изображение формируется из нескольких тематических слоев. Комбинирование этих слоев само по себе является достаточно мощным средством для визуального анализа географических объектов и явлений. В секциях Layer файла описания карты определяются параметры отображения одного слоя карты: источник данных, максимальный и минимальный масштабы, в которых слой отображается на карте, графические атрибуты отображения, классификация по некоторому полю таблицы.
В качестве основного источника данных для построения карты в MapServer используются shape-покрытия, получаемые из ГИС ArcView, в которой покрытия SHP/SHX являются рабочим форматом, или из любой другой ГИС путем экспорта в обменные форматы. Атрибутные данные для объектов покрытия хранятся в DBF-файле, в котором каждая запись соответствует объекту с идентичным порядковым номером в покрытии.
Внутри слоя декомпозиция карты производится на основе классификации объектов по значениям определенного поля DBF-таблицы, название которого указано при помощи ключевого слова Classitem. Далее для каждого значения или интервала значений в секции Class файла описания определяется тематический класс. Здесь определяются цвета, которыми объекты класса будут показаны на карте, шаблоны линий, заливки полигонов. Принадлежность объектов к описываемому классу определяется в теге Expression.
Картографическая легенда формируется Mapserver автоматически на основе названий классов и стилей их отображения в картографических слоях. В описании Legend в качестве опций можно выбрать размер легенды в пикселях, различные изобразительные стили, а также способ изображения легенды. Легенда записывается в отдельном графическом файле или встраивается в изображение карты. Масштабная линейка карты описывается объектом Scalebar. Здесь задается стиль ее отображения – размер в пикселях, цвет, шрифты. Масштабная линейка также встраивается в изображение карты.
Как и в большинстве векторных ГИС, в MapServer имеется возможность обращения к атрибутным данным по графическому изображению объекта. Для этого в описании слоя указывается объект Query - запрос к DBFтаблице. Пользователь получает результат запроса в виде HTML-страницы, формируемой на основе шаблона. Шаблон представляет собой текст, форматированный в HTML, в котором в произвольных местах вставлены особые элементы – названия полей DBF-таблицы, ограниченные квадратными скобками. В процессе синтаксического разбора текста шаблона Mapserver подменяет эти элементы реальными значениями из DBF-файла.
Функционирование Web-интерфейса карты описывается в секции Webобъекта карты. С его помощью могут быть изменены масштаб и экстент карты. Для навигации предусмотрен объект Reference Map – заранее подготовленное уменьшенное изображение исходной карты. В описании этого объекта задается имя файла изображения и его размер в пикселах. Изображение в Reference Map должно быть в той же системе координат, что и карта.
Размещение растровых карт. Сервер MapIT!.
Программное обеспечение MapIt! разработано на Python и представляет собой серверное WEB-приложение для публикации растровых изображений: отсканированных карт и космических снимков. Для работы MapIt! требуется любой web-сервер, поддерживающий динамические страницы CGI (лучшее быстродействие MapIt показывает на серверах Apache и Caudium). Пользователи просматривают карты при помощи Интернет-браузера (рисунок 16.5). Сервер MapIT! прекрасно подходит для создания как карт-путеводитей, для туристов с мобильным Интернетом в кармане, но ограниченные возможности не позволяют использовать эту систему в более серьезных задачах.

Рисунок 16.5 – WEB-интерфейс MapIt! (карта с сайта www.mapit.de)
Система MapIT! возможно является самой простой из программ для WebGIS. Для подготовки Mapit! к работе с данными пользователя имеется набор утилит, позволяющих, нарезать большую карту или снимок на "черепицы" ("tiles"). Масштаб и реальные координаты черепиц растра задаются в текстовом файле. Интерактивно возможно изменять масштаб в заданных заранее границах, а также отображать поверх растра точечные объекты. На рисунке 16.5 на растровую карту наложены железнодорожные станции, подземные станции, почтовые отделения, больницы и гаражи. Выбирая из предложенного списка типы объектов, пользователь получает разные карты.
Потребности общества в цифровых моделях местности, космических снимках, картах и продуктах их обработки и анализа постоянно растут. Пространственные данные являются основой кадастра, необходимы для оценки природных ресурсов и мониторинга окружающей среды, планирования развития территорий, маршрутизации транспорта и во многих других областях. В будущем задачи ГИС останутся прежними: они так же будут использоваться для управления географическими данными, пространственного анализа и передачи его результатов пользователям. При этом, должно быть, изменится техника реализации этих задач. Усилится значимость геоданных при принятии решений, и увеличится доля ответственности ГИС-специалистов за достоверность продуктов пространственного анализа.
Программное обеспечение ГИС сейчас достигло того уровня развития, когда решены практически все поставленные несколько десятилетий назад задачи по обработке пространственной информации. Разработчики ГИС периодически выпускают новые версии программ, но изменения в них касаются в основном улучшения интерфейса и уменьшения времени выполнения операций путем использования особенностей новых операционных систем. Функционально ГИС, выпущенная 10 лет назад, отличается от современной системы незначительно. Поэтому дальнейшее развитие ГИС-технологий может произойти только за счет качественного скачка (рисунок 17.1).

Рисунок 17.1 – Направление развития ГИС-технологий
В будущем, вероятно, облегчатся процедуры ввода геоданных. Cреди источников информации значительную часть занимают бумажные топографические и тематические карты, созданные по традиционной технологии без учета того, что их впоследствии понадобится векторизовать. Сейчас карты создаются при помощи ГИС, а данные дистанционного зондирования и цифровые модели рельефа поставщики поставляют сразу в цифровой форме. Поэтому в ближайшем будущем проблема ввода данных постепенно будет терять свою значимость, и те 75% затрат на создание ГИС, которые по некоторым оценкам уходят в ГИС-проекте на сбор и ввод данных, превратятся в 5%. Освободившиеся ресурсы будут использованы на разработку аналитических процедур, что и определит развитие ГИС на ближайшие десятилетия.
На рисунке 17.1 показано, что затраты на работу с атрибутной информацией останутся неизменными. Сейчас табличные данные в ГИС хранятся и обрабатываются средствами внутренних или внешних реляционных баз данных, в которых модель данных и функциональные возможности были установлены в 1980-х и с тех пор мало изменялись. В настоящее время предпринимаются попытки приспособить для хранения атрибутных данных XML. Для хранения пространственных данных в будущем могут использоваться промышленные реляционные базы данных, а не данные в специализированные форматы ГИС.
В будущем можно ожидать дальнейшего развития вычислительной техники. Появятся компьютеры, выполняющие вычисления еще быстрее, увеличатся объемы оперативной памяти и жестких дисков, но качественного скачка, подобного тому, что произошел в 1990-е с появлением персональных компьютеров, уже не произойдет. В 1970-80-е годы основным сдерживающим фактором в развитии ГИС была недостаточная производительность и невысокая надежность компьютеров. В 1990-е годы на первый план вышли вопросы программного обеспечения, а в XXI веке – данные.
Основными техническими проблемами в области геоинформатики сейчас являются обеспечение доступности данных, внедрение в программное обеспечение ГИС моделей неопределенности и распространения ошибок, подготовка метаданных, создание протоколов передачи геоданных в компьютерных сетях, развитие свободного программного обеспечения ГИС, но отнюдь не быстродействие средств вычислительной техники.
Влияние на ГИС должно оказать появление массивов жестких дисков емкостью порядка петабайта (1015) и сверхскоростных сетей. Это позволит создавать распределенные хранилища пространственных данных высокого разрешения на территорию всей планеты и в разные моменты времени. Появление Интернет-сервиса Google Earth подтверждает это предположение. Можно также ожидать развития ГИС-технологий за счет конверсии оборонных технологий. Так система GPS – изначально созданная для военных – успешно используется сейчас в мирных целях и весьма популярна.
Возможности пространственного анализа в ГИС будут изменяться от статического описательного анализа к симуляции и моделированию географических явлений. Исторически сложилось так, что современные ГИС унаследовали структуру данных от двумерных бумажных географических карт, которые могут показывать ситуацию “как есть” или “как было”. В будущем будет возможна визуальная симуляция развития явлений по поступающим в реальном времени измерениям с реальных сенсоров – т.е. будет смоделирована виртуальная реальность. Эти модели будут показывать ситуацию “как есть” или “как может быть”. Уже сейчас ГИС включают средства для работы с 3D-моделями; в будущем появится возможность работы с четвертым измерением – временем.
1. Берлянт, А.М. Картография: Учебник для вузов / А.М. Берлянт. – М.: Аспект Пресс, 2001. – 336 с.
2. Бугаевский, Л.М. Преобразования координат из одной картографической проекции в другую / Л.М. Бугаевский, Ю.И. Маркузе // Известия высших учебных заведений. Геодезия и аэрофотосъемка. – 2000. – №6. – С.3-19.
3. Васмут, А.С. Автоматизация и математические методы в картосоставлении: Учеб. пособие для вузов / А.С. Васмут, Л.М. Бугаевский, А.М. Портнов. – М.: Недра, 1991г. – 391 с.
4. Вахрамеева, Л.А. Математическая картография: Учебник для вузов / Л.А. Вахрамеева, Л.М. Бугаевский, З.Л. Казакова. – М.: Недра. – 1986. – 286 с.
5. Дьяков, Б.Н. Геодезия. Общий курс: Учеб. пособие для вузов /
Б.Н. Дьяков. – Новосибирск: Изд-во Новосиб. ун-та, 1993. – 171 с.
6. Замай, С.С. Программное обеспечение и технологии геоинформационных систем / С.С. Замай, О.Э. Якубайлик. – Красноярск: Изд-во СО РАН, 1998. – 100с.
7. Киенко, Ю.П. Введение в космическое природоведение и картографирование: Учебник для вузов / Ю.П. Киенко. – М.: Картгеоцентр – Геодезиздат. – 1994. – 212 с.
8. Кошкарев, А.В. Геоинформатика / А.В. Кошкарев , В.С. Тикунов. – М.: Картоцентр-Геоиздат. – 1993. – 213с.
9. Никитин, А.А. Становление и развитие геоинформатики в СССР и России / А.А. Никитин // Геоинформатика. – 1998. –№3. – С.55–56.
10. Прэтт, У. Цифровая обработка изображений / У. Прэтт. – М.: Мир, 1982. – Кн.1. – 320 с. – Кн.2. – 780 с.
11. Тикунов, В.С. Моделирование в картографии: Учебник / В.С. Тикунов. –
М.: Изд-во МГУ, 1997. – 405 c.
12. Шлихт, Г.Ю. Цифровая обработка цветных изображений / Г.Ю. Шлихт. – М.: Издательство ЭКОМ, 1997. – 336 с.
13. Краткий топографо-геодезический словарь / Б.С. Кузьмин, Ф.Я. Герасимов, В.М. Молоканов и др. изд 3-е, перераб. И доп. М., Недра, 1979, 310с.
14. Коновалова Н.В., Капралов Е.Г. Введение в ГИС. Учебное пособие. Изд-е 2-е исправленное и дополненное. М.: 1997, – 160 с.
15. Берлянт А.М., Гедымин А.В., Кельнер Ю.Г. и др. Справочник по картографии. – М.: Недра, 1988 – 421 с.
16. Геоинформатика. Толковый словарь основных терминов / Под. ред. А.М. Берлянта и А.В. Кошкарева. М.: ГИС-Ассоциация, 1999.
17. Геоинформационное картографирование. Пространственные данные, цифровые и электронные карты. Общие требования. ГОСТ Р 50828-95. М.: Изд-во стандартов, 1996.
18. Королев Ю.К. Общая геоинформатика. Часть 1. Теоретическая геоинформатика. Выпуск 1. М.: СП ООО «Дата+», 1998.
19. Кузнецов О.Л., Никитин А.А. Геоинформатика. М.: Недра, 1992.
20. Прэтт У. Цифровая обработка изображений в 2 кн. М.: Мир, 1982.
21. Новиков Ф.А. Дискретная математика для программистов. СПб.: Питер, 2001.
22. Цикритзис Д., Лоховски Ф. Модели данных. М.: Финансы и статистика, 1986.
23. Берлянт А.М. Геоинформационное картографирование. М.: МГУ, РАЕН, 1997.
24. Инструментарий геоинформационных систем / Б.С. Бусыгин, И.Н. Гаркуша, Е.С. Середин, А.Ю. Гаевенко. Киев: ИРГ «ВБ», 2000.
25. Майкл Н., Де Мерс. Геоинформационные системы. Основы. М.: Дата+, 1999.
26. Халугин Е.И., Жалковский Е.А., Жданов Н.Д. Цифровые карты / Под. ред. Е.И. Халугина. М.: Недра, 1992.
27. Шайтура С.В. Геоинформационные системы и методы их создания. Калуга: издатель Бочкарева И.Ф., 1998.
28. Лобанов А.Н., Журкин И.Г. Автоматизация фотограмметрических процессов. М.: Недра, 1980.
29. С.В. Агапов, Фотограмметрия сканерных снимков, М.: Геоиздат, 1996г.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.