
Лекция № 4
Представление информации с помощью систем счисления
1. Позиционные и непозиционные системы счисления
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления.
Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Системы счисления бывают позиционные (величина, которую обозначает цифра в записи числа, зависит от положения цифры в этом числе) и непозиционные (величина, которую обозначает цифра в записи числа, не зависит от положения цифры в этом числе).
Римская непозиционная система счисления. Самой распространенной из непозиционных систем счисления является римская. В качестве цифр в римской системе используются: I (1), V (5), Х (10), L (50), С (100), D (500), М (1000).
Значение цифры не зависит от ее положения в числе. Например, в числе XXX (30) цифра Х встречается трижды и, в каждом случае, обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.
Величина числа в римской системе счисления определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа — прибавляется. Например, запись десятичного числа 1998 в римской системе счисления будет выглядеть следующим образом:
![]()
Позиционные системы счисления. Первая позиционная система счисления была придумана еще в древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, т.е. в ней использовалось шестьдесят цифр! Интересно, что до сих пор при измерении времени мы используем основание, равное 60 (в 1 минуте содержится 60 секунд, а в 1 часе — 60 минут).
В девятнадцатом веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем дюжину (число 12): в сутках две дюжины часов, круг содержит тридцать дюжин градусов и т.д.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе.
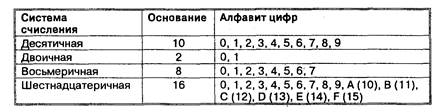
Наиболее распространенными в настоящее время позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная. Каждая позиционная система имеет определенный алфавит цифр и основание.
Цифры – знаки (символы), используемые в системах счисления для обозначения чисел.
Алфавит системы счисления – совокупность цифр и букв, с помощью которых в позиционной системе счисления записываются числа.
Основание позиционной системы счисления – количество цифр в алфавите.
В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения цифр соседних разрядов числа.
Десятичная система счисления имеет алфавит цифр, который состоит из десяти всем известных, так называемых арабских, цифр и имеет основание, равное 10, двоичная — две цифры и основание 2, восьмеричная — восемь цифр и основание 8, шестнадцатеричная — шестнадцать цифр (в качестве цифр используются и буквы латинского алфавита) и основание 16.
Десятичная система счисления. Наиболее распространенной позиционной системой счисления является десятичная система. Рассмотрим в качестве примера десятичное число 555. Цифра 5 встречается трижды, причем самая правая обозначает пять единиц, вторая справа — пять десятков и, наконец, третья — пять сотен.
Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим. Например, в десятичной системе крайняя справа позиция соответствует первому разряду, в котором цифра обозначает единицы. Цифра, смещенная на одну позицию влево, обозначает десятки, еще левее — сотни, затем тысячи и т.д.
Число 555 записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10.
В развернутой форме записи числа такое умножение производится в явной форме. Так, в развернутой форме запись числа 555 в десятичной системе будет выглядеть следующим образом:
![]()
Как видно из примера, число в позиционных системах счисления записывается в виде суммы числового ряда степеней основания (в данном случае 10), в качестве коэффициентов которых выступают цифры данного числа.
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 555,55 в развернутой форме будет записываться следующим образом:
![]()
В общем случае в десятичной системе запись числа А10, которое содержит n целых разрядов числа и m дробных разрядов числа, производится следующим образом:
![]()
Коэффициенты аi в этой записи являются цифрами десятичного числа, которое в свернутой форме записывается следующим образом:
![]()
Из вышеприведенных формул видно, что умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд вправо или влево. Например:
![]()
В системах счисления с основанием q (q-ичная система счисления) числа в развернутой форме записываются в виде суммы ряда степеней основания с коэффициентами, в качестве которых выступают цифры 0, 1, q-1.
В развернутой форме число в системе счисления с основанием q (q-ичная система счисления) записывается следующим образом:
![]()
Коэффициенты а в этой записи являются цифрами числа, записанного в q-ичной системе счисления.
2. Системы счисления, используемые в ЭВМ: двоичная,
восьмеричная, шестнадцатеричная
В двоичной системе основание равно 2, а алфавит состоит из двух цифр (0 и 1). Следовательно, числа в двоичной системе в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.
Например, развернутая запись двоичного числа выглядит следующим образом:
![]() а в свёрнутой форме:
а в свёрнутой форме:
![]()
В общем случае в двоичной системе запись числа А2, которое содержит n целых разрядов числа и m дробных разрядов числа, производится следующим образом:
![]()
Коэффициенты а в этой записи являются цифрами (0 или 1) двоичного числа, которое в свернутой форме записывается следующим образом:
![]()
Из вышеприведенных формул видно, что умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд вправо или влево. Например:
![]()
Так, в восьмеричной системе основание равно восьми (q = 8), тогда написанное в свернутой форме восьмеричное число А8 = 673,28 в развернутой форме будет иметь вид:
![]()
В шестнадцатеричной системе основание равно шестнадцати (q = 16), тогда написанное в свернутой форме шестнадцатеричное число А16 = 8А,F16 в развернутой форме будет иметь вид:
![]()
Если выразить шестнадцатеричные цифры через их десятичные значения (А = 10, F = 15), то запись числа примет вид:
![]()
Запись чисел в каждой из систем счисления с основанием q означает сокращённую запись выражения an-1*qn-1 + an-2*qn-2 + … a1*q1 + a0*q0 + a-1*q-1 + … a-m*q-m (a – цифры системы счисления; n, m – число целых и дробных разрядов соответственно).
Пример: 347,528 = 3*82 + 4*81 + 7*80 + 5*8-1 + 2*8-2.
Двоичная система, удобная для компьютеров, неудобна для человека из-за её громоздкости и непривычной записи.
Компьютер использует двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
· для её реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток – нет тока, намагничен – не намагничен и т. п.);
· представление информации посредством только двух устойчивых состояний надёжно и помехоустойчиво;
· возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
· двоичная арифметика намного проще десятичной.
Недостаток двоичной системы – быстрый рост числа разрядов, необходимых для записи чисел.
Перевод чисел из десятичной системы счисления в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
3. Основные алгоритмы перевода чисел из одной системы
счисления в другую
Перевод чисел.
1) из десятичной системы в любую другую позиционную систему и наоборот:
1. Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы счисления (q) до тех пор, пока не получим частное меньше делителя, т.е. меньше q.
2. Получить искомое число, для чего записать полученные остатки в обратной последовательности.
В качестве примера рассмотрим перевод десятичного числа 19 в двоичную систему, записывая результаты в таблицу:
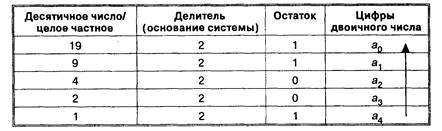
В результате получаем двоичное число:
![]()
2) При переводе числа из любой другой позиционной системы счисления в десятичную нужно представить это число в виде суммы степеней основания его системы счисления (т.е. записать число в развёрнутой форме и вычислить его значение):
Примеры:
1F316 = 1*162 + 15*161 + 3*160 = 49910
10,112 = 1*21 + 0*20 + 1*2-1 + 1*2-2 = 2 + 0 + 0,5 + 0,25 = 2,7510
6758 = 6*82 + 7*81 + 5*80 = 384 + 56 + 5 = 44510
3) из восьмеричной и шестнадцатеричной систем счисления в двоичную и наоборот:
Для перевода целого двоичного числа в восьмеричное его нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней левой группе окажется меньше, чем три разряда, то необходимо ее дополнить слева нулями.
Переведем таким способом двоичное число 1010012 в восьмеричное:
![]()
Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (групп по 3 цифры) в восьмеричные цифры.

Для перевода дробного двоичного числа в восьмеричное необходимо разбить его на триады слева направо и, если в последней правой группе окажется меньше разрядов, дополнить ее справа нулями. далее, необходимо триады заменить на восьмеричные числа.
Например, преобразуем дробное двоичное число А2 = 0,1101012 в восьмеричную систему счисления:

Получаем А8 = 0,658.
Для перевода целого двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры (тетрады), начиная справа, и, если в последней левой группе окажется меньше разрядов, дополнить ее слева нулями, для перевода дробного двоичного числа в шестнадцатеричное необходимо разбить его на тетрады слева направо и, если в последней правой группе окажется меньше, чем четыре разряда, то необходимо ее дополнить справа нулями.
Затем необходимо преобразовать каждую группу в шестнадцатеричную цифру, воспользовавшись для этого предварительно составленной таблицей соответствия двоичных тетрад и шестнадцатеричных цифр.
Переведем целое двоичное число А2 = 1010012 в шестнадцатеричное:

В результате имеем А16 = 2916.
Переведем дробное двоичное число А2 = 0,1101012 в шестнадцатеричную систему счисления:

Получаем А16 = 0,Е416.
Для перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную необходимо цифры числа преобразовать в группы двоичных чисел. Для перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в группу из трех двоичных разрядов (триаду), а при преобразовании шестнадцатеричного числа — в группу из четырех разрядов (тетраду).
Например, преобразуем дробное восьмеричное число А8 = 0,478 в двоичную систему счисления:
![]()
Получаем А2 = 0,1001112.
Переведем целое шестнадцатеричное число А16 = АВ16 в двоичную систему счисления:
![]()
В результате имеем А2 = 101010112.
Полезно знать!
|
десятичная |
двоичная |
восьмеричная |
шестнадцатеричная |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
2 |
10 |
2 |
2 |
|
3 |
11 |
3 |
3 |
|
4 |
100 |
4 |
4 |
|
5 |
101 |
5 |
5 |
|
6 |
110 |
6 |
6 |
|
7 |
111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
101 |
11 |
9 |
|
10 |
1010 |
12 |
A |
|
11 |
1011 |
13 |
B |
|
12 |
110 |
14 |
C |
|
13 |
1101 |
15 |
D |
|
14 |
110 |
16 |
E |
|
15 |
111 |
17 |
F |
4. Двоичная арифметика
Правила выполнения четырёх арифметических операций (сложение, вычитание, умножение, деление) в десятичной системе счисления нам хорошо известны – это сложение, вычитание, умножение столбиком и деление уголком. Эти правила применимы и ко всем другим позиционным системам счисления.
Сложение
|
+ |
0 |
1 |
|
0 |
0 |
1 |
|
1 |
1 |
10 |
Важно обратить внимание на то, что при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда значение числа в нем становится равным или большим основания. Для двоичной системы счисления это число равно двум.
Сложение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей сложения с учетом возможных переносов из младших разрядов в старшие. В качестве примера сложим в столбик двоичные числа 1102 и 112
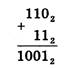
Вычитание
При вычитании цифры вычитаются по разрядам, и если при этом возникает недостаток, то происходит заём в старших разрядах.
Рассмотрим вычитание двоичных чисел. В его основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой.
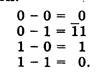
Вычитаниё многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей вычитания с учетом возможных заемов в старших разрядах. В качестве примера произведем вычитание двоичных чисел 1102 и 112
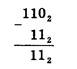
Умножение
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм умножения чисел в столбик, но при этом результаты умножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
В основе умножения лежит таблица умножения одноразрядных двоичных чисел:
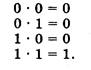
Умножение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей умножения по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на очередную цифру множителя. В качестве примера произведем умножение двоичных чисел 1102 и 112
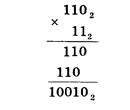
Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.
Деление
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление уголком в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулём или единицей.
Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. В качестве примера произведем деление двоичного числа 1102 на 112
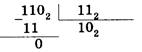
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.