Мастерская исследования линейной функции

Паспорт практики

Приложение Этапы реализации мастерской исследования линейной функций в динамической среде Desmos

Подготовительный этап

Перед проведением мастерской у учащихся 7 класса необходимо провести первые уроки по изучению линейной функции, ее графика и некоторых ее свойств. Обучающиеся 8-9 классов уже изучили данную функциональную зависимость.

Исследование линейной зависимости производится с помощью готовой активности «Игра marbles: прямые и параболы», разработанные

Л. Рождественской.

Для организации мастерской с данным ресурсом педагогу необходимо:

1.                 Перейти на сервис https://teacher.desmos.com/. Войти под своей учетной записью.

2.                 Открыть ресурс «Игра marbles: прямые и параболы» и назначить либо для созданного ранее класса, либо получить код для одного урока, нажав

на кнопку .

3.                 Выбрав срок действия, педагог получит код для учеников. Нажав на

кнопку  педагог открывает доступ к активности для учащихся.

4.                 В открытой активности необходимо задать темп  и выбрать только 1-3 слайда. Далее по ходу занятия необходимо поэтапно открывать слайды для работы групп.

5.                 Для этапа актуализации педагогу необходимо подготовить интерактивный тест Plickers или PanQuiz.

1   этап. Организационный.

Этап мотивации (самоопределения) к учебной деятельности

Основной целью этапа мотивации (самоопределения) к учебной деятельности является выработка на личностно значимом уровне внутренней готовности выполнения нормативных требований учебной деятельности.

Учитель проверяет готовность классного помещения к уроку. Проводит организационную беседу с классом. Обучающиеся отвечают на приветствие и на вопросы учителя.

2   этап. Индукция

Этап актуализация и фиксирование индивидуального затруднения в пробном действии

Цель этапа является подготовка мышления учащихся, организация осознания ими внутренней потребности к построению учебных действий и фиксирование каждым из них индивидуального затруднения в пробном действии.

«Индукция» («наведение») — создание эмоционального настроя, мотивирующего деятельность каждого, включение чувств, подсознания, формирования личностного отношения к предмету обсуждения. Индуктор — образ, фраза, текст, рисунок — все, что может вызвать поток ассоциаций, воспоминаний, ощущений, вопросов.

В режиме реального времени педагог проводит опрос в интерактивной среде Plickers или PanQuiz. В Plickers в отличие от PanQuiz ученикам не нужны мобильные телефоны и доступ к интернету, а учитель мгновенно видит результаты тестов на своём телефоне. Применение интерактивных опросов повышает вовлеченность школьников в процесс обучения позволяя усилить интерес к теме урока.

Вопросы теста:

Анализ ответов учащихся 8 классов показал, что подавляющее большинство учащихся считают, что функция — это некоторое выражение (42 %), формула (23 %). Лишь 19 % определяли функцию как зависимость. Большинство обучающихся (93%) верно определяют вид графика линейной функции как прямую. Однако также не умеют определять график функции по уравнению и путаются в количестве точек для построения графика линейной функции.

С       помощью   наводящих вопросов    подводит   обучающихся      к формулированию темы урока «Исследования линейной функций». Сообщает учащимся общие задачи урока и порядок работы.

3   этап. Самоконструкция

Выявления места и причины затруднения

Основная цель этапа – организовать анализ учащимися возникшей ситуации и на этой основе выявить места и причины затруднения, осознать то, в чем именно состоит недостаточность их знаний, умений или способностей.

Для этого необходимо, чтобы учащиеся: проанализировали шаг за шагом с опорой на знаковую запись всех вопросов теста и проговорили вслух, что и как они делали.

4   этап. Самоконструкция

Построения проекта выхода из затруднения

Основной целью этапа является постановка целей учебной деятельности и на этой основе – выбор способа и средств их реализации.

1.       Педагог представляет интерактивную систему систему Desmos. Обучающимся нужно зайти на сервис https://student.desmos.com/ и набрать код

для урока. Нажать кнопку , ввести имена и фамилии и нажать кнопку

2.       На первом активности обучающимся необходимо нажать на кнопку

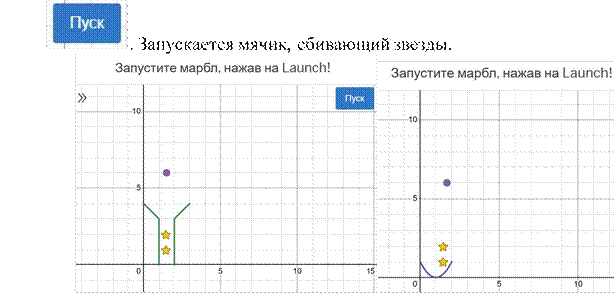
3.       Далее педагог переходит на 2 слайд. На экранах обучающихся также в режиме реального времени активность автоматически переходит на 2 слайд. На 3 слайде педагог вместе с учениками подбирают коэффициент функции =𝑘+ таким образом, чтобы прямая прошла либо по звездочкам, либо немного ниже. При этом упавший мяч смог собрать все звезды.

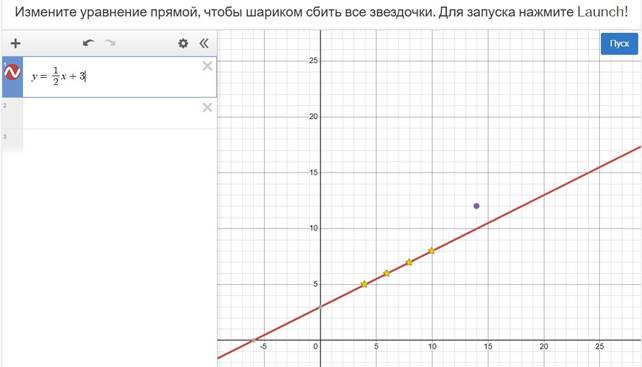
На этом слайде знакомство с системой заканчивается. Дети формулируют план выхода из затруднения и средство, которое им поможет.

5   этап. Социоконструкция.

Реализации построенного проекта.

Основной целью этапа является построение учащимися нового способа действий и формирование умений его применять как при решении задачи, вызвавшей затруднение, так и при решении задач такого класса или типа вообще.

Учащиеся в парах работают над слайдами 4-7. Учащиеся соотносят коэффициенты линейной функции с ее графиком. Проверяют правильность выполнения нажатием кнопки Пуск.

Задания с решением представлены ниже:

6   этап. Социализация

Этап первичного закрепления с проговариванием во внешней речи.

Основной целью этапа является усвоение учащимися нового способа действия при решении типовых задач.

Учащиеся работают в группах по 4 человека над заданиями со слайдов 10-11. Педагогом назначается один мастер, который следит за тем, чтобы не происходило подавление, игнорирование мнения, позиции отдельных учеников, поддерживает атмосферу сотрудничества, взаимопомощи. Все участники группы предлагают решение сложной задачи, проводят эксперимент и делают выводы внутри группы. Групповая работа обеспечивает интеграцию идей, вариантов, вопросов, проблем, разработку модели, совместную корректировку решения задачи.

Учащиеся соотносят коэффициенты линейной функции с ее графиком. Проверяют правильность выполнения нажатием кнопки Пуск. Задания с решением представлены ниже:

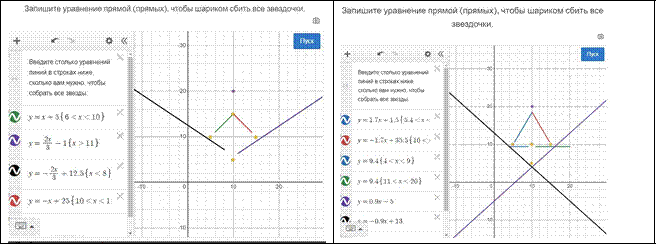
Можем заметить, что не все дети справляются с поставленной задачей. Обучающиеся предлагают самые разные способы решения данных заданий. При ограничении времени можно выполнить только одно задние из двух.

Решения представляются с панели учителя.

7. Этап самостоятельной работы с самопроверкой по эталону

Основной целью этапа является интериоризация (переход извне внутрь) нового способа действия и исполнительская рефлексия (коллективная и индивидуальная) достижения цели пробного учебного действия, применение нового знания в типовых заданиях.

Ученики индивидуально (или в парах) самостоятельно работают над слайдами 8-9. Проверяют правильность выполнения нажатием кнопки Пуск. Задания с решением представлены ниже. Эталон решения в конце этапа может быть представлен с панели учителя.

8 этап. Афиширование и разрыв

Этап включения в систему знаний и повторения.

Основной целью этапа является повторение и закрепление ранее изученного и подготовка к изучению следующих разделов курса, выявление границы применимости нового знания и использование его в системе изученных ранее знаний, повторение учебного содержания, необходимого для обеспечения содержательной непрерывности, включение нового способа действий в систему знаний.

На этом этапе учащиеся в своих группах оформляют конспект поведения линейной функции и представляют свои работы, знакомятся с коллективными работами других групп. Шаблон для заполнения представлен ниже:

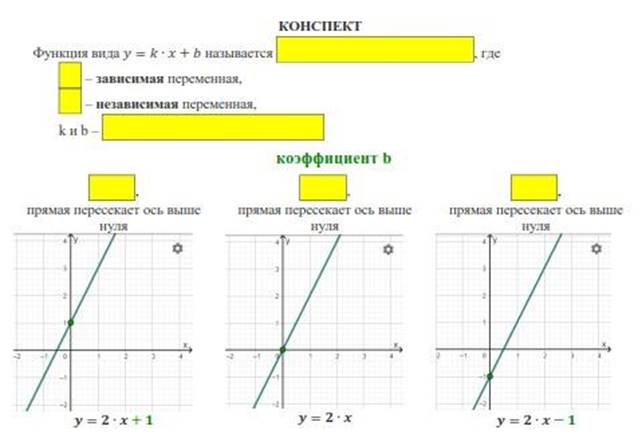
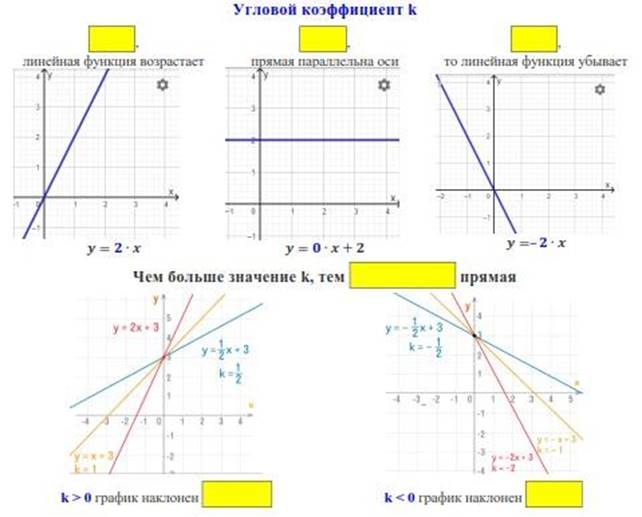
После представления конспектов педагог ставит перед детьми новые вопросы:

ü Какие будут коэффициенты у совпадающих прямых?

ü При каком условии графики линейных функций будут параллельными прямыми?

ü При каком условии графики линейных функций будут перпендикулярные прямыми?

ü При каком условии графики линейных функций будут пересекающиеся прямыми?

ü Почему коэффициент k называется угловым коэффициентом?

ü Какая функция называется прямой пропорциональностью?

Разрыв – внутреннее осознание участниками мастерской неполноты или несоответствия своего прежнего знания новому, внутренний эмоциональный конфликт, подвигающий к углублению в проблему, к поиску ответов, к сверке нового знания с научным источником. На данном этапе каждый участник мастерской должен осознать разнообразие вариантов решения задач 10-11, необходимость получения дополнительной информации, которая позволит лучше вникнуть в суть вопроса, адекватно оценить разнообразие ответов на него.

9 этап. Рефлексия

Рефлексивный анализ учебной деятельности на уроке

Основной целью этапа является самооценка учащимися результатов своей учебной деятельности, осознание метода построения и границ применения нового способа действия.

Рефлексия – отражение чувств, ощущений, возникающих у участников в процессе мастерской. Происходит анализ выполненной работы, оценивается эмоциональное состояние и удовлетворенность учеников от результатов их индивидуального, парного и группового труда.

На последнем слайде обучающимся необходимо самостоятельно построить график функции вида = 𝑘+ одним из трех цветов, которые соответствуют настроению от работы.

Можно усложнить задание, задав коэффициенты линейной зависимости:

k – качество индивидуальной работы (чем больше коэффициент тем в большей степени удовлетворен собственной работой, отрицательный коэффициент говорит о низко степени самостоятельности) b – групповая работа (положительный значение коэффициента – признак качественной работы в группе всех участников, отрицательное значение – работа в группе мешала индивидуальной работе).

При проведении занятия педагогу необходимо помнить, что учитель в мастерской превращается в мастера, который демонстрирует одно действие за другим, позволяя ученикам выполнять посильные задания, высказывать предположения, учит слышать товарищей, делать открытия. Каждое последующее задание дополняет, расширяет, углубляет знания учащихся, помогает им понять что-то новое. В мастерской важен не только результат творческого поиска, но и сам процесс.

В мастерской приняло участие 85 обучающихся 8 классов МАОУ гимназия №18. Фрагмент панели учителя представлен на рисунке:

Большинство ребят высказало положительные отзывы о проведенной мастерской.