МКОУ Тастахская ООШ им. М.В. Петровой

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Доклад на тему:

«Математический кружок в 5 классе»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Выполила:

Винокурова Н.М.,

учитель математики

 

 

 

 

 

 

 

2023

Оглавление

Введение. 4

1.   Математический кружок в 5-ом классе. 6

2. План занятий математического кружка учащихся 5-х классов и методические рекомендации к ним   8

3. Содержание занятий математического кружка в 5-ом классе. 11

Заключение. 33

Список использованной литературы.. 34

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

Математика признана интеллектообразующим учебным предметом. Знания, умения и навыки, полученные школьниками на уроках математики, развиваются, расширяются, углубляются, находят практическое применение при хорошо организованной внеклассной работе, которая является неотъемлемой частью учебно-воспитательного процесса.

Внеклассная работа по математике формирует и развивает способности и личность ребёнка. В условиях малокомплектной школы внеурочная деятельность по математике является не только средством для углубления математических знаний, но средством вовлечения учащихся в познавательную деятельность, средством организации досуга учащихся в сельской местности.

Математический кружок - одна из наиболее действенных и эффективных форм внеклассных занятий. В основе кружковой работы лежит принцип строгой добровольности. Обычно кружковые занятия организуются для хорошо успевающих учащихся. Однако следует иметь в виду, что иногда и слабо успевающие учащиеся изъявляют желание участвовать в работе математического кружка и нередко весьма успешно занимаются там; учителю математики не следует этому препятствовать. Необходимо лишь более внимательно отнестись к таким учащимся, постараться укрепить имеющиеся у них ростки интереса к математике, проследить за тем, чтобы работа в математическом кружке оказалась для них посильной. Конечно, наличие слабо успевающих учащихся среди членов математического кружка затрудняет работу учителя, однако путем индивидуализации заданий, предлагаемых учителем кружковцам, можно в некоторой степени ослабить эти трудности. Главное - сохранить массовый характер кружковых занятий по математике, являющийся следствием доступности посещения кружковых занятий всеми желающими.

Внеклассная работа по математике в малокомплектной школе имеет ряд преимуществ:

-                     небольшая наполняемость класса позволяет вести учет индивидуальных особенностей учащихся;

-                     организации познавательной деятельности проводится с учетом учебных и индивидуальных потребностей и интересов детей;

-                     восполняется недостаток времени на уроке для развития общих и частных умений и навыков;

-                     реализуется система стимулирования участия учащихся во внеклассных мероприятиях.

Внеклассная работа, проводимая в условиях малокомплектной школы, имеет свои специфические особенности:

-                     внеклассные занятия и мероприятия учитывают запросы отдельной группы учащихся или индивидуальные наклонности каждого ученика;

-                     занятия организуются на добровольных началах;

-                     конкурсы и викторины проводятся между класс-комплектами или между смежными классами;

-                     команды для участия в конкурсах могут быть «сборными», состоящими из учащихся одного класс-комплекта;

-                     позволяют учащимся проявить свой интерес к определенным видам занятий, предусмотренных планом внеклассной работы.

Математический кружок является одной из самых значительных форм дополнительного математического образования. Это обуславливается тем, что:

-                     кружковая форма работы является доступной для всех школ, так как ее реализация не требует больших материальных затрат и специального оборудования и позволяет охватить достаточно большое количество учащихся;

-                     по форме проведения кружковые занятия являются схожими с урочными, в то же время они имеют большие возможности, по сравнению с урочными занятиями, в приобщении учащихся к новым формам работы: деловым и ролевым играм, докладам, викторинам, соревнованиям, лабораторным и практическим работам и другим.

Доклад состоит из вводной части, основного материала, заключения.

Цель: Разработка заданий для занятий математического кружка в 5 классе, направленных на повышение уровня математического образования и развития учащихся, и рекомендаций по их использованию.

Задачи:

§     изучение литературы с целью ознакомления с формами кружковых занятий и отыскания наиболее интересных и занимательных задач;

§     разработка заданий для математического кружка и рекомендаций по их использованию.

 

 

 

 

 

1.   Математический кружок в 5-ом классе

Основной формой внеклассной работы по математике  являются математические кружки. В 5 классе планируется проводить по одному занятию в 2 недели на определённую тему.

К организации работы математического кружка целесообразно привлекать самих учащихся (поручать им подготовку небольших сообщений по изучаемой теме, подбор задач и упражнений по конкретной теме, подготовку справок исторического характера, изготовление моделей и рисунков к данному занятию и т. д.). На занятиях математического кружка учитель должен создать "атмосферу" свободного обмена мнениями и активной дискуссии

На первом занятии кружка надо наметить основное содержание работы, выбрать старосту кружка, договориться с учащимися о правах и обязанностях члена кружка, составить план работы и распределить поручения за те или иные мероприятия (выпуск математической стенной газеты, ведение документации работы кружка и т. п.).       

Посредством кружковой работы с учащимися 5-6 классов основной школы можно развить их интерес к математике, обеспечить повышение уровня математического образования и развития учащихся, если:

-                     кружковая работа строится на основе определенной совокупности принципов, ориентированных на достижение основных целей математического образования;

-                     программа кружковой работы содержит материал, как занимательного характера, так и дополняющий программу общеобразовательной школы по математике, и обеспечена соответствующим методическим оснащением;

-                     работа математического кружка осуществляется с учетом индивидуального подхода к обучению учащихся с использованием активных форм и методов познавательной деятельности учащихся.

Для проведения кружковых занятий применяются различные формы работы:

1)                 изготовление наглядных пособий и самодельных приборов для практических работ по курсу математики, графические иллюстрации задач, черчение графиков и диаграмм, составление рисунков к докладам и пр.;

2)                 выпуск математических бюллетеней, математических газет;

3)                 проведение экскурсий математической направленности;

4)                 организация и проведение математических олимпиад;

5)                 организация и проведение математических вечеров.

Рекомендуется использование следующего материала:

1)                 занимательные исторические задачи;

2)                 упражнения со спичками;

3)                 занимательные квадраты, головоломки;

4)                 математические фокусы;

5)                 более трудные и интересные задачи, связанные с программным материалом.

Рекомендуется комбинированное тематическое занятие, основную часть которого составляет решение задач на определенную тему. Каждую задачу разбирают самым подробным образом, не переходят к следующей задаче, пока предыдущая не решена полностью и не сделаны все возможные обобщения, дополнения и выводы.

Помимо этой основной формы проведения кружковых занятий, рекомендуется ещё несколько форм:

1)                 «десятиминутка» - небольшое сообщение учителя или ученика по какому-нибудь сравнительно узкому вопросу;

2)                 решение задач, не связанных с основной темой данного заседания;

3)                 математические фокусы, задачи-шутки, геометрические иллюзии, игры и развлечения, не связанные с основной темой заседания;

4)                 разбор домашних задач;

5)                 доклады на математические и историко-математические темы;

6)                 моделирование;

7)                 математические экскурсии;

8)                 обсуждение математических книг и статей;

9)                 сообщение учащегося о самостоятельно составленной и решенной задаче;

10)             чтение отрывков из художественных произведений, связанных с математикой.

Обучение в 5-м классе – это весьма подходящий период для того, чтобы начинать формировать и развивать интерес к математике. Заметим, что в этот период у подростка формируются психические новообразования. Например, произвольность всех психических процессов, смысловая логическая память, понятийное мышление. Теперь уже, в отличие от младшего школьника, подросток может самостоятельно организовать свое внимание, память, мышление, воображение. Его мышление приобретает способность к гипотетико-дедуктивным рассуждениям. Подросток становится способным к умственным экспериментам, к мысленному решению задач на основе каких-то предположений. Предметом мышления становится не только решение заданных задач, но и сам процесс мышления. Появление критичности в восприятии окружающего мира способствует появлению потребности в доказательствах. Это позволяет начинать систематическое изложение математического материала, повысить научный уровень изложения. Со способными к математике учащимися можно изучать и некоторые теоретические положения.

Содержание, формы и методы кружковой работы учащихся должны учитывать некоторые общие идеи для реализации оптимального подхода в обучении. Целесообразно использовать специальные упражнения на занятиях математического кружка, способствующие более глубокому усвоению программного материала и развитию учащихся.

Каждый ребенок даже при самых неблагоприятных условиях обладает собственным ментальным опытом. Значит, имеется отправной интеллектуальный уровень, а также у каждого ребенка существует диапазон возможного наращивания его интеллектуальных сил, связанных с обогащением и усложнением ментального опыта. Главное – создать определенные условия для становления его интеллектуальных возможностей.

 

 

2. План занятий математического кружка учащихся 5-х классов и методические рекомендации к ним

Содержание занятий разработано из расчета одно занятие в  две недели, что составляет 18 занятий за учебный год. Некоторые темы, предлагаемые для изучения на занятиях математического кружка, напрямую не связаны с изучением программного материала. Это такие темы как «Принцип Дирихле», «Арифметика Магницкого» и др. Они представлены на занятиях математического кружка для формирования и развития интереса учащихся к математике в процессе ее изучения.

Все задачи, подобранные к изучению каждой темы, соответствуют принципам посильной трудности, научности и связи содержания занятий с учебной программой по математике.

План занятий математического кружка учащихся 5-х классов:

1)                 цифры у разных народов мира;

2)                 поиски закономерностей;

3)                 решение уравнений;

4)                 решение задач с помощью уравнения;

5)                 геометрические головоломки;

6)                 сообщения о великих математиках;

7)                 площади и объемы;

8)                 логические задачи;

9)                 обсуждение олимпиадных задач;

10)             задачи на части;

11)             десятичные дроби;

12)             математический час по теме «Десятичные дроби»;

13)             принцип Дирихле;

14)             конкурс математических газет;

15)             арифметика Магницкого;

16)             мир процентов и среднего арифметического;

17)             викторина;

18)             вечер веселых и смекалистых.

Методические рекомендации к занятиям.

На первых занятиях кружка большое внимание уделяется организационным моментам, закладывается основа для формирования активного интереса к математике. Поэтому материал для первых занятий кружка необходимо подбирать так, чтобы он был ясен и понятен учащимся, не вызывал неуверенности в своих силах; в то же время он должен быть интересным, использовать исторический и занимательный материал.

Первое занятие в 5 классе посвящается римской системе счисления и начинается с беседы учителя, опирающейся на исторический материал, выполняются задания на перевод числа из арабской нумерации в римскую и обратно. Цель данного занятия - более подробное ознакомление учащихся с римскими цифрами и их использованием на практике. Эти цифры употребляются для записи номеров месяцев года, номеров томов и глав книг и т.п. Естественно, учащийся должен быть готов к восприятию таких записей – уметь записывать римские цифры и правильно их понимать. В этом заключается образовательное и воспитательное значение рассматриваемой темы занятия на кружке. На этом же занятии используются разнообразные игровые задания.

Вторая тема посвящена поискам закономерностей. Упражнения на данную тему призваны развивать у учащихся наблюдательность, интуицию, смекалку, потребность увидеть весь заложенный в упражнения смысл, увидеть закономерность. Эти упражнения способствуют развитию трудолюбия, упорства в достижении конкретной цели.

Занятие на тему: «Геометрические головоломки» знакомит учащихся, в игровой форме, с некоторыми элементами геометрии, развивает пространственное мышление.

Все занятие шестой темы посвящено сообщениям о великих математиках. Учащиеся выступают в роли докладчиков. Они заранее выбирают тему, советуются с учителем, находят нужную им литературу, обрабатывают и систематизируют собранный ими материал. Занятие можно построить следующим образом:

ü    учащиеся разбиваются на 2 группы, в зависимости от количества учащихся;

ü    каждая группа готовит сообщение об одном известном математике, но так, что каждый член группы будет докладывать об определенном периоде жизни ученого;

ü    в момент выступления первой группы, вторая слушает и фиксирует важные моменты, потом группы меняются ролями;

ü    в конце занятия подводится итог в форме викторины (вопросы к викторине готовит учитель).

В 5 – ом классе одно из занятий посвящается решению логических задач с помощью таблиц.

Занятие по теме «Десятичные дроби» проводится в форме соревнования. Выигрывает тот, кто набирает больше баллов. Целесообразно, чтобы учащиеся дома заготовили красные карточки, по которым можно судить, кто первым будет отвечать. Следующее занятие по этой же теме проводится в форме математического часа. Итогом соревнований является объявление команды победителей и их награждение. Эти занятия объединяют учащихся, дают почувствовать ответственность за других членов команды.

Занятие по теме «Принцип Дирихле» следует начать с рассмотрения конкретного примера.

Пример: В магазин привезли 34 ящика с яблоками трех сортов, причем в каждом ящике лежали яблоки какого-то одного сорта. Можно ли найти 12 ящиков с яблоками одного сорта?

Решение: Предположим, что мы раскладываем в 33 ящика яблоки трех сортов. Если распределять их не поровну, то хотя бы один сорт будет помещен в 12 и более ящиков, что нас уже устраивает. Самый неблагоприятный для нас случай, когда мы получаем по 11 ящиков каждого сорта. Но у нас есть еще один ящик, 34–ый, в который мы должны положить яблоки какого-либо из трех сортов, т.о можно утверждать, что по крайней мере в 12 ящиках находятся яблоки одного сорта.

Данная тема способствует развитию мышления учащихся, умению на практике видеть приложения весьма абстрактных и общих математических теорий.

На одном из занятий в конце года проводится викторина. Составлением вопросов могут заниматься двое кружковцев, которые на этом занятии будут помогать учителю. Учащиеся разбиваются на две команды. Учитель читает вопрос, та команда, которая быстрее поднимет красную карточку (она заранее приготовлена) и правильно ответит на заданный вопрос получает 1 балл. В конце викторины подсчитываются баллы. Побеждает та команда, которая наберет больше баллов.

Математические вечера могут стать одной из самых интересных и любимых учащимися форм работы. Однако, чтобы помимо интереса данная форма работы стала еще и результативной в развитии математических способностей, необходимо тщательно выбирать темы для проведения вечеров, проводить подготовительную работу с ребятами.

 

3. Содержание занятий математического кружка в 5-ом классе

Занятие №1.

«Цифры у разных народов».

Рассказать об арабской и римской нумерации. В ходе беседы решить задачи:

1.                  Записать арабскими цифрами: ХХV, CХIV, XCII, MMDLXXI.

2.                  Записать римскими цифрами: 37, 92, 2164, 3068, 4527, 183693.

3.                  В данных неверных равенствах переложить по одной «спичке», чтобы все равенства стали верными:

а)VI- IV=IX; б) VI-IV=XI; в) VI+IV=XII; г) X+X=I; д) X-IX=VI; е) VIII+IV=XVII; ж) IV-I+V=II; з) X=VII-III.

4. Фокус: (отгадывание задуманного числа)

Задумайте любое число, умножьте его на 2, прибавьте 1, полученный результат увеличьте в5 раз, вычтите 4, умножьте на 2. Что у вас получилось? (Если от названного числа отнять 2, а затем полученное число разделить на 20, то получим задуманное число.)

5.На одной из старых улиц Москвы стоят два дома, на фасаде которых обозначена дата их постройки: а)MDCCCCV б) MDCCCLXXXXIX

В каком году построен каждый дом?

Домашнее задание:

v    Запишите арабскими цифрами числа: XXXIV; XXIX; CDXXI; CMIII.

v    Запишите римскими цифрами числа: 49; 574; 1147; 1974; 5003.

v    Этот греческий храм построен из 11 спичек. Требуется переложить 4 спички так, чтобы получилось 15 квадратов.

 

 

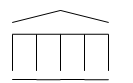
Занятие №2.

«Поиски закономерностей».

1.                  Найдите правило нахождения числа, помещенного в окошке чердака. Вставьте число в свободное окошко.

 

 

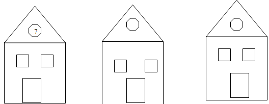
2.                  Найдите число на «голове».

 

 

3.                  Вставьте пропущенное число, если числа в табличках составлены по одному и тому же закону.

 

11

12

15

16

14

6

15

7

?

8

10

7

 

4.                  Игра «Стертая цифра».

Участникам игры предлагается написать какое-нибудь многозначное число, например 6745693, а затем переставить в нем цифры любым образом, например 5937466. Найти разность полученных чисел, в данном примере:

В полученной разности предлагается стереть одну из цифр (кроме нуля) и подсчитать сумму оставшихся цифр, по которой ведущий и угадывает стертую цифру. Например, в рассматриваемом примере решили стереть цифру 7, тогда 8+0+8+2+2=20. Далее, ведущий от 27 отнимает 20 и получает зачеркнутую цифру.

Домашнее задание:

v    Найдите правило составления последовательности чисел и вставьте вместо звездочки пропущенное число: 5; 14; 41; 122; * ; 1094.

v    Впишите недостающие числа в таблицу:

2

6

12

20

30

42

Занятие №3.

«Решение уравнений».

1.                  4х + 5 = 7х - 4;

2.                  5а – 7 = 3а – 1;

3.                  4(у + 2)= 3(3у - 4);

4.                  Игра «Лесенка». Каждый играющий получает карточку, на которой нарисована лесенка, в строчках ее по две клеточки. По сигналу ведущего все играющие пишут любое двузначное число на верхней ступеньке. Затем сносят последнюю цифру написанного числа в следующую строчку по вертикали. К снесенной цифре приписывают вторую цифру так, чтобы получилось нечетное число. Затем опять сносят последнюю цифру по вертикали в следующую строчку и приписывают одну цифру так, чтобы полученное вновь число делилось на 3, далее на 4, на 5 и т.д до 10. Выигрывает тот, кто первым правильно закончит «лесенку».

Домашнее задание:

v    Решите уравнение: 5х +3х – 2 = 2(3х + 5);

v    Решите уравнение: 8(х+3) = 75 – (х-3);

v    Составьте условие задачи, которая решалась бы с помощью уравнения: 4(х-5)=3х-2. Решите её.

Занятие №4.

«Решение задач с помощью уравнения».

1.                  На одной чаше весов лежат 6 одинаковых яблок и 3 одинаковые груши, на другой чаше- 3 таких же яблока и 5 таких же груш. Весы находятся в равновесии. Что легче: яблоко или груша?

2.                  Сын спросил отца, сколько ему лет. Отец ответил: «Если к половине моих лет прибавить 12, то узнаешь, сколько мне было 12 лет назад». Сколько лет отцу?

3.                  Витя задумал двузначное число, в котором цифра десятков в 2 раза меньше цифры единиц. Если цифры в этом числе переставить, то полученное обращенное число будет на 36 больше задуманного. Найти задуманное Витей число.

4.                  Игра: пройдите все незаштрихованные клетки квадрата так, чтобы ни в одной не побывать дважды и вернуться к начальной клетке. Обход начните с клетки, в которой стоит крестик. По диагонали ходить нельзя.

 

 

5.                  У Володи и его отца сегодня день рождения. Отец старше сына ровно в 11 раз. Через 6 лет он будет старше сына только в 5 раз. Сколько лет сыну и сколько отцу?

Домашнее задание:

v    Турист проехал поездом, на автомобиле и на велосипеде всего 900 км. На автомобиле он ехал со скоростью 45 км /ч, на велосипеде – 15 км /ч. Поездом он проехал на 90 км больше, чем на велосипеде. Сколько часов турист ехал на автомобиле и сколько на велосипеде, если путь, пройденный им на автомобиле, вчетверо больше пути, пройденного на велосипеде?

v    Библиотекой куплено на равные суммы несколько одинаковых книг по математике и одинаковых – по литературе. Известно, что книг по литературе на 20 меньше, чем по математике. Сколько куплено тех и других книг, если одна книга по литературе стоит 63 руб., а одна книга по математике – 35 руб.?

v    В трех ящиках лежат орехи. В первом ящике на 6 орехов меньше, чем в двух других вместе, а во втором – на 10 меньше, чем в первом и третьем вместе. Сколько орехов в третьем ящике?

Занятие №5.

«Геометрические головоломки».

1.                  (Домашняя заготовка: вырезаны 16 одинаковых квадратов четырех цветов – по 4 квадрата каждого цвета). Сложите из них квадрат 4 на 4 так, чтобы одинаковые цвета не повторялись:

a)                  ни в строчках, ни в столбцах;

b)                 ни в строчках, ни в столбцах, ни по диагонали.

Зарисуйте решения в тетрадь, используя цветные карандаши или фломастеры.

2.                  На четырех квадратах каждого цвета напишите цифры 1, 2, 3, 4. Сложите теперь квадрат 4 на 4 так, чтобы одинаковые цифры и одинаковые цвета не повторялись ни в строках, ни в столбцах, ни на диагоналях квадрата.

3.                  Из спичек построен дом. Переложить две спички так, чтобы дом повернулся другой стороной.

 

 

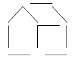
4.                  Из 10 спичек сделан ключ. Переложить в нем 4 спички так, чтобы получилось три квадрата.

 

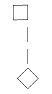
5.                  Имеются 4 куска проволоки длиной 18 см каждый. Как из них сделать каркасную модель параллелепипеда с размерами 8 см, 4 см и 6 см, не разрезая этих кусков проволоки?

Домашнее задание:

v    На коврике изображено 7 роз. Требуется тремя прямыми линиями разрезать коврик на 7 частей, каждая из которых содержала бы по одной розе.

 

 

 

 

 

 

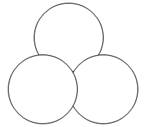
v    Не отрывая карандаш от бумаги и не обводя дважды один и тот же участок, вычертить фигуру, изображенную на рисунке.

Занятие №6

«Сообщения о великих математиках».

Процесс работы над докладом состоит из следующих этапов:

1.                  выбор темы;

2.                  составление плана доклада;

3.                  определение источников, литературы и знакомство с ними;

4.                  обработка и систематизация собранного материала;

5.                  написание доклада.

Занятие №7

«Площади и объемы».

1.                  У Маши был аквариум, основание которого – квадрат со стороной 24 см; уровень воды в нем достигал 36 см. Купили новый аквариум длиной 36 см, шириной 24 см. Маша перелила воду в новый аквариум. Определите уровень воды в новом аквариуме.

2.                  Из листа бумаги, размер которого 950 на 1200 мм2 можно вырезать или квадраты со стороной 64 мм, или квадраты со стороной 46 мм.Какие квадраты надо вырезать, чтобы получилось меньше отходов?

3.                  Прямоугольный параллелепипед, длина которого 4 см, ширина 3 см, высота 2 см, покрасили со всех сторон и разрезали на кубические сантиметры. Сколько получилось кубических сантиметров, у которых покрашена одна грань, две грани, три грани?

4.                  Витя Верхоглядкин начертил квадрат и нашел его периметр и площадь. Получилось Р=20 см, S=36 см2. Верно ли он посчитал?

5.                  В одной старинной математической рукописи шутливо обсуждалась возможность асфальтирования дороги для муравья: длиной 100 км и шириной 1 мм. Сможете ли вы найти площадь этой дороги?

Домашнее задание:

v    Разрежьте прямоугольник, длина которого 9 см, а ширина 4 см, на две равные части, из которых можно составить квадрат.

v    Объем деревянного бруска 80 см³, ширина 4 см, высота 2 см. Длину этого бруска уменьшили на 3 см. Определить объем оставшейся части.

v    Васе купили аквариум в форме куба, вмещающий 64 л воды (1 л = 1 дм³ ). Вася наполнил аквариум водой, не долив 5 см до верхнего края. Сколько литров воды он налил в аквариум?

Занятие №8.

«Логические задачи».

1.                  Милиционер обернулся на звук бьющегося стекла и увидел четырех подростков, убегающих от разбитой витрины. Через 5 минут они были в отделении милиции. Андрей заявил, что стекло разбил Виктор, Виктор же утверждал, что виноват Сергей. Сергей заверял, что Виктор лжет, а Юрий твердил, что это сделал не он. Из дальнейшего разговора выяснилось, что лишь один говорил правду. Кто разбил стекло?

2.                  В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке – не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. Куда налита каждая жидкость?

3.                  Игра «Хоп!». Играющие по очереди называют последовательные числа натурального ряда, но вместо чисел, делящихся на 3 и оканчивающихся на 3, должны говорить «хоп!». Тот, кто ошибся, выбывает из игры, а остальные продолжают играть.

4.                  Лёня, Женя и Миша имеют фамилии Орлов, Соколов и Ястребов. Какую фамилию имеет каждый мальчик, если Женя, Миша и Соколов члены математического кружка, а Миша и Ястребов занимаются музыкой.

Домашнее задание:

v    Для Вани, Толи и Миши есть три пирога: с рисом, с капустой и яблоками. Миша не любит пирог с яблоками и не ест с капустой; Ваня не любит пирог с капустой. Кто что ест?

v    Три подруги вышли в белом, зеленом и синем платьях. Их туфли были одного из тех же трех цветов. Известно, что только у Ани цвета платья и туфель совпадали. Ни платье, ни туфли Вали не были белыми. Наташа была в зеленых туфлях. Определите цвет платья и туфель каждой из подруг.

v    Поспорили три мудреца – кто из них самый мудрый. Пришли они к четвертому мудрецу с просьбой их рассудить. Подумал четвертый мудрей и предложил им такое испытание: «У меня есть 5 колпаков – два белых и три черных. Мы зайдем в темную комнату, я надену на ваши головы по колпаку. Затем мы выйдем из этой комнаты, и, кто первый определит цвет своего колпака, тот самый мудрый из вас». Согласились мудрецы и сделали все, как договорились. Через некоторое время один из них воскликнул: «На мне черный колпак!». Как рассуждал самый мудрый из мудрецов?

Занятие №9.

«Обсуждение олимпиадных задач».

1.                  Я задумал число, отнял от него 16, умножил результат на 4, разделил на 7. От 144 отнял полученное частное. 288 разделил на полученную разность, прибавил 195, получил 198. Какое число я задумал?

2.                  Ученик написал на доске пример на умножение двузначных чисел. Затем он стер все цифры и заменил их буквами. Получилось равенство: AB CD=MLNKT. Докажите, что ученик ошибся.

3.                  Баба Яга поставила на дверь кодовый замок. На замке нужно расставить девять разных цифр (1,2,3,4,5,6,7,8,9) так, чтобы получившиеся равенства были верными.

:

=

-

=

3

+

=

1

4.                  Незнайка начертил три прямых линии и отметил на них 6 точек. Оказалось, что на каждой прямой он отметил 3 точки. Покажите, как он это сделал.

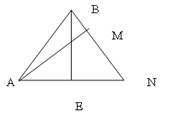
5.                  Запишите все отрезки, изображенные на рисунке. Сколько получилось всего отрезков?

6.                  Четыре мальчика выбирали водящего с помощью считалки. Тот, на кого падало последнее слово, выходил из круга, и счет повторялся заново. Считающий мальчик каждый круг начинал с себя и в результате стал водящим, причем счет каждый раз кончался перед ним. Какое наименьшее количество слов могло быть в считалке?

7.                  Имеются 4 чемодана и 4 ключа к ним. Но ключи перемешались. Сколько испытаний в худшем случае надо сделать, чтобы подобрать для каждого чемодана ключ?

Домашнее задание:

v    Три охотника варили кашу. Один положил 2 кружки крупы, второй – 1 кружку, а у третьего крупы не было. Они съели всю кашу поровну. Третий охотник и говорит: «Спасибо за кашу! - и вот вам задача: Я даю вам 5 патронов. Как поделить эти патроны в соответствии с вашим вкладом в мою порцию каши?»

v    В школе изучают три иностранных языка: английский, немецкий и французский. Каждый ученик в классе изучает 2 языка. Английский язык изучают 19 человек, немецкий – 8, французский – 11. Сколько учеников в классе?

v    На доске 5 на 5 клеток расставьте фишки так, чтобы в каждой строке и в каждом столбце стояли ровно три фишки. В одной клетке может стоять только одна фишка.

Занятие №10

«Задачи на части».

1.                  Два дня пионеры собирали лом, причем  того, что собрано в первый день, равна  того, что собрано во второй день; во второй день собрано на 690 кг больше, чем в первый. Сколько килограммов лома собрано в каждый из этих дней?

2.                  Когда велосипедист проехал  пути, лопнула шина. На остальной путь пешком он затратил вдвое больше времени, чем на велосипедную езду. Во сколько раз велосипедист ехал быстрее, чем шел?

3.                  Игра « оттесни шашку ». В крайних клетках полоски 1 на 20 стоят белая и черная шашки. Двое, по очереди, передвигают свою шашку на одну или две клетки вперед или назад, если это возможно (перепрыгивать через шашку нельзя). Проигрывает тот, кто не может двинуть свою шашку. Кто побеждает при правильной игре - первый или второй?

4.                  В классе число отсутствующих учеников составляет  часть от числа присутствующих. После того как из класса вышел один ученик, число отсутствующих стало равно  числа присутствующих. Сколько учеников в классе?

5.                  Два крестьянина вышли из деревни в город. Когда прошли  пути, они сели отдохнуть. «Сколько нам еще осталось идти?» - спросил один попутчик другого. «Нам осталось на 12 км больше, чем мы прошли»,- был ответ. Каково расстояние между городом и деревней?

Домашнее задание:

v    Когда пассажир проехал половину всего пути, то лег спать и спал до тех пор, пока не осталось ехать половину того пути, что он проехал спящим. Какую часть пути он проехал спящим ?

v    На собрании присутствуют около 80 школьников. Треть из них – девочки, половина которых учится в 6-м классе. Из присутствующих мальчиков  не учатся в 6-м классе. Сколько учащихся 6-го класса присутствуют на собрании?

v    Решив все сбережения поделить поровну между всеми своими сыновьями, помещик составил такое завещание: «Старший из моих сыновей должен получить 1000 руб. и  часть остатка; следующий – 2000 руб. и  нового остатка; третий сын – 3000 руб. и  часть третьего остатка » и т.д. Определить число сыновей и размер завещанного сбережения.

Занятие №11

«Десятичные дроби».

Соревнование: (выигрывает тот, кто набирает больше баллов).

Ø    Что легче: 0,3 килограмма железа или 0,3 килограмма ваты?

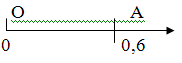
Ø    Восстановите координатный луч, т.е отложите на нем единичный отрезок.

Однажды учитель предложил Вите Верхоглядкину сравнить дроби 0,31 и 0,6. «Это очень просто, - начал Витя. – Целые части этих дробей равны. Сравним дробные части: 31 больше 6, значит, и 0,31 больше чем 0,6». Согласны ли вы с таким решением?

Ø    Некоторое число удовлетворяет одновременно трем неравенствам. Найдите его:

2,11< <2,5;

2,4 < <2,72;

2,39< <2,42.

Ø    В некоторой десятичной дроби все цифры одинаковы. Какое это число, если оно больше 2,21, но меньше 2,221?

Ø    Найдите ошибку:

a)                  3,27 3,3;

b)                 2,99 3,0;

c)                  12,34 12,3;

d)                 0,75 0,7;

e)                  8,18 8,2.

Ø    Все числа: 2,5; 2,6; 2,7; 2,8; 2,9; 3,1; 3,2; 3,3; 3,4 обладают одной особенностью, связанной с округлением чисел. Какой?

Ø    Витя задумал число. Сначала он округлил его до десятых, получилось 6,4. Потом он округлил задуманное число до целых, получилось 7. Не ошибся ли он?

После подсчета баллов объявляются победители первых трех призовых мест и им вручаются небольшие сувениры.

1.                  Три друга – Коля, Витя, и Миша – решили купить шайбу, которая стоит 1 рубль. У Коли и Вити было по 0,25 руб., а у Миши – 0,45 рублей. Будут ли они вечером играть в хоккей?

2.                  Вместо звездочек поставьте знаки «+» или «-» так, чтобы равенства были верными: а) 5,5 * 1,9 * 2,6 =1;

б) 7,9 * 3,4 * 4,2 = 7,1;

в) 6,1* 13,5 * 12,4 =5.

Домашнее задание:

v    Вместо квадратиков запишите такие десятичные дроби, чтобы равенства оказались верными:

v    Даны числа: 0,8; 1,6; 2,9; 3,7. Разность двух из них равна одному из оставшихся чисел. Запишите это равенство.

v    В трех пакетах содержится 1,5 кг крупы, причем массы первого и второго пакетов составляют вместе 1,3 кг, а второго и третьего – 0,9 кг. Сколько крупы в каждом пакете?

Занятие №12

Математический час по теме « Десятичные дроби».

Девиз: Знания имей отличные по теме: «Дроби десятичные».

Весь класс разбивается на две команды.

1.                  Соревнование «Думай и соображай».

Задачи предлагаются всему классу. Отвечает тот, кто первый поднял руку. За правильное решение – 5 баллов. Эти баллы выставляют в таблицу той команде, в которой состоит ученик, решивший задачу.

a)                  Между числами 5,2 и 5,3 поставьте число, большее 5,2 и меньшее 5,3.

b)                 Даны числа: 0,3 ; 7,7; 0,125. Поставьте между ними такие знаки, чтобы в результате выполнения указанных ими действий получилась 1.

c)                  Найдите устно значение выражения: (13- 2,46 : 3,54)(0,5- ).

d)                 Некоторое число удовлетворяет одновременно трем неравенствам. Найдите его:

e)                  3,5 < < 4,1;

3,7< < 4,0;

3,6 < < 3,9.

2.                  Игра « Заполни клетку».

Две команды получают листочки, текст которых приведен ниже.

 

 

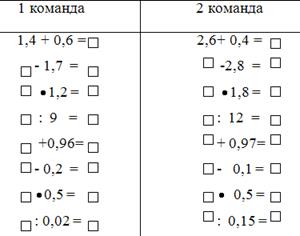
Правило заполнения клеток состоит в том, что ответ предыдущего действия становится в первую клетку следующего. Первый участник команды вычисляет первый пример и передает карточку следующему участнику команды и т.д. Выигрывает та команда, которая быстрее и правильно заполнит карточку.

(У первой команды ответ 20, а у второй – 3).

3.                  Игра «Сравни дроби».

На доске прикреплены две таблицы (по одной для каждой команды). В каждой клетке написана десятичная дробь. Дроби в таблицах одинаковы, но расположены по-разному.

 

 

0,3	2,06	5,4
1,48	0,08	0,29
5,39	2,1	1,5

 

0,08	1,48	1,48
1,5	1,5	0,3
5,4	2,06	2,1

 

Учащимся предлагают в течение одной минуты рассмотреть числа в таблице, мысленно располагая их в порядке возрастания. Затем учащиеся в командах выстраиваются друг за другом. По знаку ребята, стоящие в команде первыми, бегут одновременно к таблицам и указывают на них самое маленькое число. Каждый следующий игрок указывает большее число. Он выбегает тогда, когда предыдущий возвратится и встанет в конец строя.

Начисление баллов идет по двум критериям: кто быстрее?, кто без ошибок?.

Итог математического часа подводит учитель. Объявляется команда победителей. Вручаются призы. В качестве выигрыша могут быть чертежные инструменты, недорогие, но необходимые учащимся принадлежности, наконец, конфеты, яблоки и т.д.

Домашнее задание:

v    Даны числа: 2,67; 3,75; 3,51; 2,43. Сумма двух из них равна сумме оставшихся. Запишите это равенство.

v    Масса драгоценных камней измеряется в каратах, причем 1 карат равен 0,2 гр. Геолог нашел два алмаза. Первый – массой 51 карат, а второй – массой 10,1 гр. Какой алмаз ценнее?

v    Задумайте две десятичные дроби. Из большего числа вычтите меньшее. Результат запишите. Теперь сложите задуманные числа. Результат запишите. Потом сложите полученные результаты и сумму разделите на 2. Получится одно из задуманных чисел. Объясните почему?

Занятие №13

«Принцип Дирихле».

1.                  В магазин привезли 25 ящиков с яблоками трех сортов, причем в каждом ящике лежат яблоки какого-то одного сорта. Можно ли найти 9 ящиков с яблоками одного сорта?

2.                  Принесли 5 чемоданов и 5 ключей от этих чемоданов, но неизвестно, какой ключ от какого чемодана. Сколько проб придется сделать в самом худшем случае, чтобы подобрать к каждому чемодану свой ключ?

3.                  В ящике лежали вперемешку 6 белых и 10 голубых носков. Каково наименьшее число носков надо взять из ящика, не глядя в него, чтобы иметь не меньше одной пары носков одного цвета?

4.                  Семь грибников собрали 100 грибов, причем все грибники собрали разное число грибов. Докажите, что есть трое грибников, которые собрали не меньше 50 грибов.

5.                  Игра «минус на плюс». В строке написано несколько минусов. Двое, по очереди, переправляют один или два соседних минуса на плюс. Выигрывает тот, кто переправит последний минус. Кто выиграет при правильной игре?

Домашнее задание:

v    В классе 30 человек. В диктанте Витя Малеев сделал 12 ошибок, а каждый из остальных – не больше. Докажите, что по крайней мере трое учеников сделали одинаковое количество(быть может, и ноль) ошибок.

v    В шкафу лежат вперемешку 5 пар светлых ботинок и 5 пар темных ботинок одинаковых размера и фасона. Какое наименьшее количество ботинок надо взять наугад из шкафа, чтобы среди них была хоть одна пара (на правую и левую ноги) одинакового цвета?

v    Сможет ли Петя разложить 44 монеты по 10 карманам так, чтобы количество монет в каждом кармане было бы различным?

Занятие №14.

«Конкурс математических газет».

На данном занятии кружка каждая группа представляет свою газету. Участники, у которых получилась самая интересная, красочная, занимательная газета, получают небольшие сувениры. Оставшуюся часть времени все учащиеся путешествуют по газете-победительнице, разгадывая ее ребусы, головоломки, кроссворды, решая интересные задачи.

Занятие №15

«Арифметика Магницкого».

«Арифметика, сиречь наука числительная, с разных диалектов на славянский язык переведенная и во едино собрана …»

Л.Ф. Магницкий.

1.                  Доклад о Л.Ф. Магницком.

2.                  Некий человек нанял работника на год, обещав дать ему 12 руб. и кафтан, но тот, проработав 7 месяцев, восхотел уйти и просил достойной платы с кафтаном; хозяин дал ему по достоицу расчет 5 руб. и кафтан, и ведательно есть, коликой цены оный кафтан был.

3.                  Послан человек из Москвы в Вологду, и велено ему в хождении своем совершати на всякий день по 40 верст; потом другий человек и другий день послан в след его и велено ему идти на день 45 верст и ведательно есть, коликий день постигнет второй первого?

4.                  Некто купил 96 гусей. Половину гусей он купил, заплатив по 2 алтына и 7 полушек за каждого гуся. За каждого из остальных гусей он заплатил по 2 алтына без полушки. Сколько стоит покупка?

5.                  «Математические забавы».

Пронумеровать дни недели, начиная с понедельника по порядку с 1 до 7. Кто-нибудь задумал день. Нужно угадать, какой день он задумал. Угадывающий предлагает выполнить про себя следующие действия:

1.                  умножить номер задуманного числа на 2;

2.                  прибавить к произведению 5;

3.                  умножить сумму на 5;

4.                  приписать к произведению нуль и назвать результат.

От этого числа угадывающий отнимает 250 и получает номер задуманного дня недели.

Домашнее задание:

v    Летели скворцы и встретились им деревья. Когда сели они по одному на дерево, то одному скворцу не хватило дерева, а когда на каждое дерево сели по два скворца, то одно дерево осталось не занятым. Сколько было скворцов и сколько было деревьев?

v    Путешественник идет из одного города в другой 10 дней, а второй путешественник тот же путь проходит за 15 дней. Через сколько дней встретятся путешественники, если выйдут одновременно навстречу друг другу из этих городов?

v    Один человек купил 112 баранов старых и молодых, заплатив за них 49 рублей и 20 алтын. За старого барана он платил по 15 алтын и по 4 полушки, а за молодого барана по 10 алтын. Сколько каких баранов было куплено?

(гривна – 10 копеек; алтын – 3 коп; полушка-  коп.).

Занятие №16

«Мир процентов и среднего арифметического».

1.                  Собрали 100 кг грибов. Оказалось, что их влажность 99%. Когда грибы подсушили, влажность снизилась до 98%. Какой стала масса грибов после подсушивания?

2.                  Рост человека археологи могут определить даже по отдельным костям. Например, длина малой берцовой кости составляет 22% роста человека, а локтевой кости составляет 16% роста человека.

a)                  При раскопках нашли малую берцовую кость длиной 39,3 см. Вычислите, каков был рост человека.

b)                 Как можно доказать, что локтевая кость длиной 20,3 см не могла принадлежать тому же человеку?

3.                  Сеня купил три пакета орехов, а Саша – 2 таких пакета. К ним присоединился Костя, и они разделили все орехи поровну. При расчете оказалось, что Костя должен уплатить товарищам 25 коп. Сколько денег из этой суммы должен получить Сеня и сколько Саша? Сколько стоит пакет орехов?

4.                  Средний возраст 11-ти футболистов команды 22 года. Во время игры один из игроков получил травму и ушел с поля. Средний возраст оставшихся на поле игроков стал 21 год. Сколько лет футболисту, ушедшему с поля?

5.                  Фокус «Опять пять!».

Задумайте натуральное число, прибавьте к нему следующее за ним по порядку, добавьте к результату 9, разделите на 2, вычтите задуманное число. «А теперь я знаю, сколько у вас получилось!»- «Сколько?»- «5!».

Домашнее задание:

v    Цена входного билета на стадион была 180 руб. После снижения входной платы число зрителей увеличилось на 50%, а выручка выросла на 25%. Сколько стал стоить билет после снижения?

v    У горного барана массой 150 кг масса рогов равна 30 кг. Сколько процентов составляет масса рогов от массы тела: 20% или 25%?

v    Трое жильцов готовят обед на одной печи. Жилица – назовем её для удобства Тройкиной – положила в общую печь 3 полена своих дров, жилица Пятеркина – 5 поленьев, жилец Бестопливный, у которого не было своих дров, получил от обеих гражданок разрешение сварить обед на общем огне. В возмещение расходов он уплатил соседкам 80 коп. Как должны они поделить между собой эту плату?

Занятие №17

«Викторина».

1.                  Пассажир такси ехал в село. По дороге он встретил 5 грузовиков и 3 автомашины. Сколько всего машин шло в село?

2.                  У мальчика столько же сестер, сколько и братьев, а у сестры его братьев в 2 раза больше, чем сестер. Сколько в этой семье братьев и сколько сестер?

3.                  Как провести прямую, пересекающую все три стороны треугольника?

4.                  Имеется ров шириной 2 метра. Как переправиться через этот ров с помощью двух досок длиной 2 метра?

5.                  Два поезда одновременно вышли навстречу друг другу, один со скоростью 60 км/ч, а другой со скоростью 50 км/ч. На каком расстоянии будут поезда друг от друга за час до встречи?

6.                  Стоят шесть стаканов, первые три из них с водой. Как сделать, чтобы пустой стакан и стакан с водой чередовались? Разрешается брать только один стакан.

7.                  «Загадка». Чем больше из неё берешь, тем больше она становиться. Что это?

8.                  Человек рассеянный лег спать в 7.00 вечера на улице Бассейной, предварительно заведя будильник на 8.00 с тем, чтобы встать утром. Сколько он часов спал, пока его не разбудил будильник?

9.                  Что больше – 48,4% от 28 или 28% от 48,4?

10.              В коробке 15 шариков: красных, синих и зеленых. Красных шариков в 7 раз меньше, чем зеленых. Сколько в коробке синих шариков?

11.              Из 8 колец одно несколько легче остальных. Найти это кольцо не более чем двумя взвешиваниями на чашечных весах.

12.              В ящике 70 цветных карандашей: 20 красных, 20 синих, 15 зеленых, 12 желтых, 3 черных. Какое наименьшее число карандашей надо взять, не видя их, чтобы среди них было не меньше 10 карандашей одного цвета?

Занятие №18

«Вечер веселых и смекалистых».

Участвуют две команды. Вечер начинается с приветствия команд.

Команда 1:

Этот турнир ждали мы.

По нему стосковались умы.

Дружно будем задачи решать-

Мы хотим математику знать.

Как же нам не веселиться?

Не смеяться, не шутить?

Ведь сегодня на турнире

Мы решили победить!

 

Команда 2:

Сегодняшний турнир мы выиграть хотим

И просто вам победу не дадим.

Придется попотеть и постараться.

За каждое очко мы будем драться.

Смекалку мы проявим и отвагу

И просим разгадать сию бумагу.

А если вдруг не повезет? –

Победа всех когда-нибудь найдет.

 

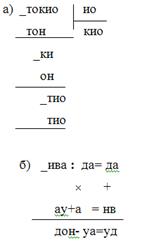
Команды обмениваются большими свитками из ватмана. Свитки разворачивают и показывают собравшимся. На них большими цветными буквами написаны ребусы. Листы вывешивают на доске. Каждая команда, собравшись в кружок, тихо разгадывает ребусы соперника.

 

 

Пока команды трудятся над ребусами, ведущий представляет жюри. Затем ведущий обращается к командам: «Для решения большинства задач недостаточно одних знаний. Необходима ещё и внимательность. С чего начинается решение задачи? Конечно, с условия. Но условие можно читать по-разному: прочтешь невнимательно - вот и утеряна главная ниточка. Проверим, умеют ли команды быстро улавливать условие задачи. Кто из вас быстрее решит задачу Корнея Ивановича Чуковского:

 

«Шел Кондрат в Ленинград,

А навстречу двенадцать ребят,

У каждого по три лукошка.

В каждом лукошке – кошка,

У каждой кошки – 12 котят,

У каждого котенка

В зубах по 4 мышонка.

И задумался старый Кондрат:

Сколько мышат и котят

Ребята несут в Ленинград?»

 

Условие кажется очень простым, и некоторые ребята торопятся сосчитать. Ведущий не перебивает их, но затем сообщает, что они плохо выслушали условие и поэтому попали в положение Кондрата:

 

«Глупый, глупый Кондрат!

Он один и шагал в Ленинград,

А ребята с лукошками,

С мышами и кошками

Шли навстречу ему –

В Кострому».

 

Разобравшись с Кондратом, ведущий снова обращается к ребусам. Представители команд докладывают о том, в чем они увидели ключ к разгадке. За расшифрованный ребус присуждается 1 балл.

Традиционная часть турнира – веселая рыбалка.

На столе – «озере» разбросаны в разных местах рыбки вырезанные из бумаги и красиво раскрашенные. К каждой рыбке скрепками прикреплена задача. Ребята должны удочкой (палочка и к ней прикреплена нить с магнитом) поймать рыбку. Но ловцы не видят рыбок: с их стороны протянута занавеска. Она загораживает стол от играющих, и они забрасывают свои удочки наугад, как настоящие рыбаки. Рыбки видны болельщикам, которые должны активно помогать своим командам. Если с помощью указаний болельщиков рыбка найдена и её удается подцепить магнитом за скрепки, то удержать не так легко. Требуется осторожность, как при обычной ловле. Наконец, счастливый рыбак держит в руках свою добычу. Ему присуждают 1 балл и дают время для обдумывания задачи. Когда и соперник вытащит рыбку, первый ловец читает вслух свою задачу, сообщает её решение. Если задача решена верно, то ученику присуждают еще 1 балл, если же нет, то он обращается за помощью к команде.

Приведу несколько заданий конкурса «Рыбалка»:

1.                  Из Москвы в Ленинград вышел поезд со скоростью 50 км/ч, а из Ленинграда в Москву вышел поезд со скоростью 60 км/ч. Какой из поездов будет дальше от Москвы в момент встречи?

2.                  Тройка лошадей пробежала 30 км. Какое расстояние пробежала каждая лошадь?

3.                  Какой знак надо поставить между двумя двойками, чтобы получить число больше двух, но меньше трех?

4.                  По стеблю растения, высота которого 1 метр, ползет улитка. Днем она поднимается на 4 дм, а ночью спускается на 2 дм. На какой день улитка будет на вершине?

5.                  Мальчик хочет 30 орехов разложить на три кучки, чтобы в каждой кучке было нечетное число орехов. Что вы ему посоветуете?

6.                  Книга в переплете стоит 1 рубль 20 коп. Сколько стоит книга, если она на 1 рубль дороже переплета?

7.                  Арбуз весит 2 кг и еще 2/3 арбуза. Какова масса всего арбуза?

Этот конкурс очень возбуждает и участников, и зрителей. Поэтому ведущий предлагает всем успокоиться и выслушать индусскую притчу, которую любил рассказывать один из создателей Московского художественного театра Константин Сергеевич Станиславский.

Магараджа выбирал себе министра. Он объявил, что возьмет того, кто пройдет по стене вокруг города с кувшином, доверху наполненным молоком, и не прольет ни капли. Многие ходили, но по пути их отвлекали, и они проливали молоко. Но вот пошел один. Вокруг него кричали, стреляли. Его всячески пугали и отвлекали. Но он не пролил молоко. «Ты слышал крики, выстрелы? – спросил его потом магараджа. – Ты видел, как тебя пугали?» - «Нет, повелитель, я смотрел на молоко».

«Не слышать и не видеть ничего постороннего – вот до какой степени может быть сосредоточено внимание. Каким мощным оно бывает. Теперь мы проверим внимание членов команд»

От каждой команды на очередной конкурс выходят по одному человеку. Начинаются игры на проверку внимания.

Слушай одновременно нескольких.

Двое говорят одновременно два различных слова, а представители команд должны различить, кто какие слова сказал. Затем трое говорят одновременно три разных слова, следом четверо – четыре слова и т.д. Выигрывает тот, кто различил больше слов.

Каждой руке – свое дело.

Играющим дают лист бумаги и в каждую руку по карандашу. Задание: левой рукой начертить 3 треугольника, а правой 3 окружности.

Шагай – соображай.

Участники этого конкурса стоят рядом с ведущим. Все делают первые шаги, и в это время ведущий называет какое-нибудь число, например 7. При следующих шагах ребята должны называть числа, кратные 7: 14, 21, 28 и т.д. На каждый шаг по числу. Ведущий идет с ними в ногу, не давая замедлить шаг. Как только кто-то ошибся, он остается на месте до конца движения другого.

По результатам всех трех игр жюри определяет команду, победившую в конкурсе «Внимание», и указывает, сколько баллов заработала каждая команда (от 1 до 3 баллов).

С большим интересом ребята ждут конкурса капитанов. И вот, наконец, они предстают в единоборстве.

Вопросы капитанам (на размышление – полминуты).

1.                  В воде оказалась 10-я ступенька пароходной веревочной лестницы. Начался прилив: вода в час поднимается на 30 см. Между ступеньками лестницы 15 см. Через сколько часов вода скроет 6-ю ступеньку?

2.                  Два в квадрате – 4, три в квадрате – 9. Чему равен угол в квадрате?

3.                  В семье у каждого из 6 братьев есть по сестре. Сколько детей в этой семье?

Последнее конкурсное соревнование вечера – для болельщиков. Кто быстрее сосчитает?

1.                  44 : 4=

44,044 : 44=

4, 444 : 44=

44,4444 : 444=

2.                  55 :5=

5,555 : 0,55 =

55,055 : 5,5 =

555,555 : 55 =

Специально не оговаривается, какие баллы жюри может присуждать капитанам или болельщикам. Договариваться об оценках нужно в начале вечера, а в конце его жюри может согласовывать оценки по ходу работы.

В дополнительное время происходят внеконкурсные состязания. Одно из них – «Аукцион пословиц и поговорок с числами». Например: «Одна голова хорошо, а две – лучше»; «Одна рука узла не вяжет; у семи нянек дитя без глазу; хвастуну цена – три копейки» и т.д.

Заканчивается вечер выступлением представителя жюри, который называет победителей и поздравляет их. Можно вручить небольшие призы.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Заключение

Цель доклада в качестве разработки заданий для занятий математического кружка в 5 классе, направленная на повышение уровня математического образования и развития интереса у учащихся к математике была достигнута. На основании проведенного анализа литературы были разработаны занятия математического кружка для 5 класса, разработаны методические рекомендации по их использованию. На занятиях использовались различные формы работы с учащимися, обеспечивающие вовлечение их в активную учебно-познавательную деятельность, что обеспечивает формирование и развитие интереса к математике, более прочные знания программного материала, его расширение и углубление, развитие таких качеств мышления, как способность к обобщению, систематичность и последовательность мышления, умение устанавливать связи между приобретенными математическими знаниями и явлениями жизни и др.

Разработанные занятия кружковой работы по математике для 5 класса содержат материал как занимательного характера, так и дополняющий программу общеобразовательной школы по математике

Наиболее интересными являются занятия, построенные в игровой форме. Учащимся очень понравились занятия, на которых присутствовали элементы соревнований, и т.д.

Список использованной литературы

1.                  Айзенберг М.И., Петрушин П.К. Некоторые формы внеклассной работы по математике // Математика в школе. – 1985.-№5.

2.                  Балк М.Б., Балк Г.Д. Математика после уроков: Пособие для учителей. – М.: Просвещение, 1971.  

3.                  Бескин Н.М. О некоторых основных принципах преподавания математики // Математика в школе, 1985.-№1.

4.                  Виленкин Н.Я., Депман И.Я. За страницами учебника математики: Пособие для учащихся 5-6 классов средней школы. - М.: Просвещение, 1989.  

5.                  Гарднер М. Математические чудеса и тайны / Под ред. Г.И.Шилова. – М.: Наука, 1986.  

6.                  Ганчев И. Математический фольклор / И. Ганчев, К. Чимев, Й. Стоянов.- М.: Знание, 1987.  

7.                  Жохов В.И. Преподавание математики в 5 и 6 классах: Методические рекомендации для учителя. – М.: Русское слово, 1999.  

8.                  Задачи для внеклассной работы по математике в 5-6 классах: Пособие для учителей / Под. ред. Д.Б. Фукса. – М.: Мирос, 1993.  

9.                  Зубелевич Г.И. Внеклассная работа по математике в 5-6 классах // Математика в школе, 1985.- №4.  

10.              Кострикина Н.П. задачи повышенной трудности в курсе математики 4-5 классов: книга для учителя. – М.: Просвещение, 1986.  

11.              Мардахаева Е.Л. Математический кружок в системе дополнительного математического образования учащихся 5-7-х классов основной школы: Дисс… канд. пед.н.-М., 2001.

12.              Математика: Учеб. Для 5 класса общеобразоват. учреждений // Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 6-е изд.- М.: Мнемозина, 2000.  

13.              Числовые ребусы и способы их решения / Л. М. Лихтарников. – СПб.: Лань, МИК, 1996.  

14.              Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4-8 классов. – 5-е изд. – М.: Просвещение, 1988.  

15.              Олехник С.Н. Старинные занимательные задачи / С.Н. Олехник, Ю.В. Нестеренко, М.К.Потапов. – М.: Дрофа, 2002.  

16.              Петраков И.С. Математические олимпиады школьников. – М.: Просвещение, 1982.  

17.              Серебровская Е.К. Опыт внеклассной работы по математике. – Иркутск: Обл. Гос. Изд., 1952.  

18.              Сидорова Е.Г. Старинные задачи // Математика в школе, 1994. - №5.  

19.              Фоминых Ю.Ф. Принцип Дирихле // Математика в школе, 1996. - №3.  

20.              Шарыгин И.Ф., Шефкин А.В. Математика: Задачи на смекалку, 5-6. – М.: Просвещение. 1996. –

21.              Шевкин А.В. Школьная олимпиада по математике.- М.: Русское слово, 2002.  

22.              Шуба М.Ю. Занимательные задания в обучении математике: Книга для учителя. – М.: Просвещение, 1994.  

23.              Щербина К.М. Математические кружки в средней школе // Математика в школе, 1940. - №3.  

24.              Кроссворды для школьников. Математика / В. Г. Мантуленко, О. Г. Гетманенко. – Ярославль: «Академия развития», 1998.  

25.              Математика: Задачи на смекалку: Учеб. пособие для 5 – 6 кл. общеобразоват. Учреждений. – 3-е изд. – М.: Просвещение, 1998.  

26.              Математические кружки в школе. 5 – 8 классы / А. В. Фарков. – 2-е изд. – М.: Айрис-пресс, 2006.  

27.              Математические олимпиады в школе. 5 – 11 классы / А. В. Фарков. – 6-е изд. – М.: Айрис-пресс, 2007.  

28.              Математика. 5 – 11 классы: предметные недели  в школе. – Вып. 2 / авт.-сост. С. В. Виноградова, Н. Н. Деменева. – Волгоград: Учитель, 2008.

29.              Математические олимпиады младших школьников: Кн. для учителя: Из опыта работы (в сел. р-нах) / В. Н. Русанов. – М.: Просвещение, 1990.  

30.              Олимпиадные задания по математике. 5 – 11 классы / авт.-сост. О. Л. Безрукова. – Волгоград: Учитель, 2009.  

31.              Олимпиадные задания по математике. 5 – 8 классы. 500 нестандартных задач для проведения конкурсов и олимпиад: развитие творческой сущности учащихся / авт.-сост. Н. В. Заболотнева. – Волгоград: Учитель, 2006.  

32.              Отдыхаем с математикой: внеклассная работа по математике в 5 – 11 классах / авт.-сост. М. А. Иченская. – Волгоград: Учитель, 2006.  

33.              Предметные недели в школе. Математика. / сост. Л. В. Гончарова. \ Волгоград, Учитель, 2006.  

34.              Игры на логику. Танграм / Пер. с англ. Слокум Джерри. – М.: Мой Мир, 2005.  

35.              Знаменитые ученые. Жизнь. Творчество. Открытия: рефераты: Математика. Химия. География / сост. Н. В. Ширшина. – Волгоград: Учитель, 2008.  

36.              Олимпиадные задания по математике. 5-6 классы / авт.-сост. Ю. В. Лепехин. – Волгоград: Учитель, 2010.  

37.              Математические чудеса и тайны; Пер. с англ./ Под ред. Г. Е. Шилова. – 5-е изд., стер. – М.: Наука. Гл. ред. Физ.-мат. лит., 1986.  

38.              Лучшие задачи на смекалку. – М.: Научно-технический центр «Университетский»: АСТ-ПРЕСС, 1999.  

39.              1000 проблемных задач по математике. – Луганск: «Учебная книга», 2006.  

 

 

 

Скачано с www.znanio.ru