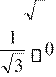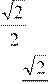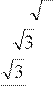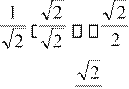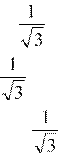Методическая разработка урока по математике по теме Решение тригонометрических уравнений

Министерство науки и образования Челябинской области

Государственное бюджетное профессиональное образовательное учреждение

«Миасский геологоразведочный колледж»

Методическая разработка урока математики на тему

«Решение простейших тригонометрических уравнений»

Выполнила преподаватель:

Новикова Светлана Ивановна

г. Миасс, 2022

Тема урока: Решение простейших тригонометрических уравнений

Учебный предмет: ОУП 04 Математика

Место урока в системе уроков: заключительный урок по теме «Решение простейших тригонометрических уравнений» Цель: Создание условий для:

- обобщения и закрепления понятия и свойств акрфунций; - закрепления навыков решения простейших тригонометрических уравнений;

- определение степени усвоения темы обучающимися.

Задачи урока:

• образовательные - обобщить и систематизировать знания, умения и навыки обучающихся по решению простейших тригонометрических уравнений;

• развивающие - развивать и совершенствовать умения применять имеющиеся у обучающихся знания; развивать логическое мышление, память, математическую речь;

• воспитательные - воспитывать у обучающихся чувство ответственности, формировать навыки самостоятельной деятельности. Тип урока: обобщение и систематизация знаний Требования к результатам освоения:

Предметные:

- знать понятие арксинуса, арккосинуса, арктангенса;

- уметь применять свойства аркфункций при решении уравнений;

- знать решение простейших тригонометрических уравнений;

- владеть устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для продолжения образования и освоения избранной профессии на современном уровне. Метапредметные:

- овладение разнообразными способами деятельности,

- приобретение и совершенствование опыта проведения доказательных рассуждений, логического обоснования выводов,

- использования различных языков математики (словесного, символического, графического) для иллюстрации, интерпретации, аргументации и доказательства;

- опыт самостоятельной работы с источниками информации, - анализа, обобщения и систематизации полученной информации, интегрирования её в личный опыт.

Личностные:

- развитие самостоятельного мышления в учебной деятельности, навыков самоконтроля;

- развитие логического мышления, алгоритмической культуры и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и её приложений в будущей профессиональной деятельности;

- воспитание культуры поведения, сопереживания успехам и неудачам товарищей.

Методы обучения: репродуктивный с опорой, наглядно-иллюстративный. Оборудование урока: сводная таблица решений простейших тригонометрических уравнений, таблица значений тригонометрических функций, ноутбук, мультипроектор.

Этап, время

Деятельность

Обоснование

преподаватель

обучающиеся

Организацион ный момент

1 мин.

Приветствует обучающихся, отмечает отсутствующих.

Слушают преподавателя,

проверяют свою готовность к уроку.

Создание рабочей обстановки в классе, мобилизация обучающихся для включения в учебный процесс.

Воспитание дисциплины и организованности.

Актуализация опорных знаний

12мин

1. Повторим свойства функции – четность и нечетность. Это нам нужно при решении самостоятельной работы.

arcsinarcsinarccosarccosarctgarctg arcctgarcctg

2. Заполнить таблицу. Эти значения arcsin и arccos нужны при решении тригонометрических уравнений.

Прослушали эти формулы и зрительно зафиксировали

Повторение и корректировка опорных знаний.



- 1

3  2

2  2



arcsin

arccos

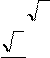
3. Вспомнить основные формулы решения

тригонометрических уравнений, чтобы не допускать ошибо при решении тригонометрических уравнений.

cost  a ; t arccosa2k ; kZ sint  a ; t 1^karcsinak kZtgt  a ; t arctgak ; kZ

4. Вспомнить частные случаи решения тригонометрических уравнений. Закончите, пожалуйста, запись, и будьте внимательны потом, при решении уравнений.

cosx1

х=…

cosx1

х=…

cosx0

х=…

sin x1

х=…

		sin x1	х=…
		sin x0	х=…
Постановка цели урока. 2 мин.	Французский писатель Анатоль Франс (1844–1924) заметил: «Что учиться можно только весело... Чтобы переварить знания, надо поглощать их с аппетитом». Последуем совету писателя: будем на уроке активны, внимательны, будем «поглощать» знания с большим желанием, ведь они скоро нам понадобятся для успешной сдачи экзамена. Сегодня у нас заключительный урок по теме “Решение простейших тригонометрических уравнений”. Повторяем, обобщаем, приводим в систему приемы решения простейших тригонометрических уравнений. Перед вами стоит задача – показать свои знания и умения по решению данных уравнений.			Внимательно слушают.	Постановка целей и задач урока.
Подготовка к обобщающей деятельности. 8 мин	Решение уравнений по теме. а) sin2x 0 2xk;kZ x_^^k;kZ 2 б) cos2x 2x arccos 2k;k Z 2x ^ 2k;k Z 3			Обучающиеся работают вместе с отвечающим у доски или решают уравнения самостоятельно и сверяют решение с записями на доске.	Повторение и анализ основных фактов.

x ^k;k Z

в) 2cosx 3 3

cosx

 3 

xarccos 2k;kZ

 2 _



x ^_^^_ 2k;k Z

 6 

x  ^ 2k;k Z

г) 3tgx 1 2

3tgx 1 tgx 

x  arctg k;k Zx^k;kZ

Воспроизведе

Самостоятельная работа:

Обучающиеся выполняют

Проверка степени усвоения материала, выявление пробелов в знаниях

ние знаний на

новом уровне

11 мин

3мин

Вариант 1

1)cosx

2) 2cosx 3  0

3) 2sin x1 0

4) tgx  3  0

Вариант 2

1)sin x 

2) 2 cosx1 0

3) 2sin x 3  0

4) tgx 

Решение:

Вариант 1

1)cosx

xarccos  2n;nZ

x ^ 2n;nZ

самостоятельную

работу,

По команде учителя обмениваются тетрадями и осуществляют взаимопроверку. Верное решение показывается на экране.

обучающихся.

2) 2cosx 3  0

2cosx

cosx

x arccos 2n;nZ

x ^ 2n;nZ

3) 2sin x1 0

2sin x1

sin x  

x  1^karcsin^_ 2 ^_k;k Z



x 1^k^_^^_k;kZ

 4 

x 1^k^¹^k;k Z

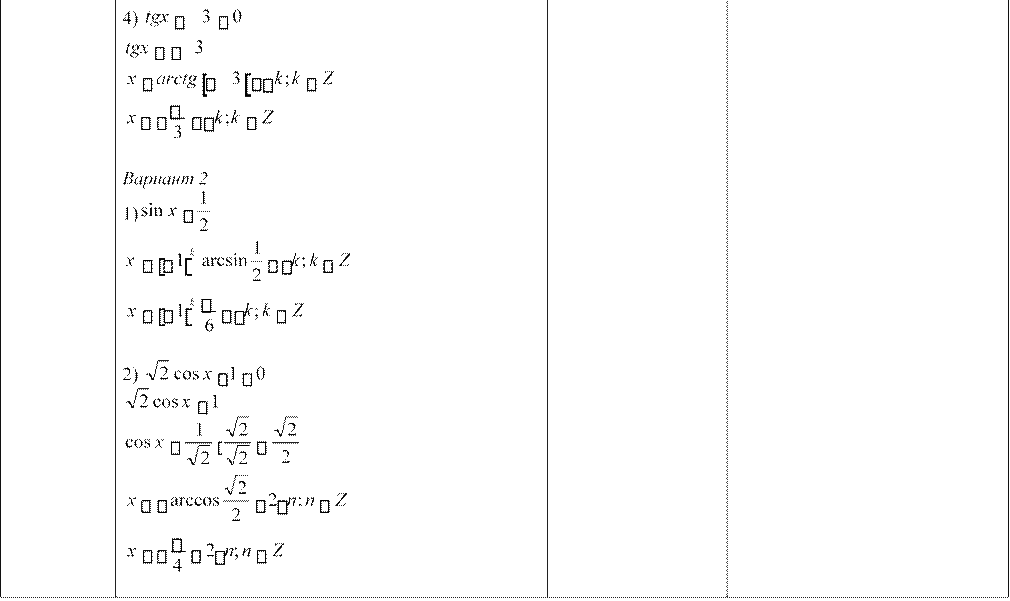
3) 2sin x 3  0

2sin x  3

sin x

x  1^karcsin^_ 2³_^k;k Z



x 1^k^_^^_k;kZ

 3 

x 1^k^¹^k;k Z 3

4) tgx   0

tgx 

x  arctg k;k Z

x ^k;k Z

5 мин.

Проверим усвоенные вами знания с помощью кроссворда (Приложение 1)

Устно отгадывают

слова в кроссворде

Проверка теоретических знаний

Рефлексия 3 мин.

Преподаватель подводит итоги урока.

Выставляет отметки. Благодарит за работу на уроке.

Делятся впечатлениями

Подведение итогов работы,

формулирование выводов

Домашнее задание.

Подготовиться к контрольной работе.

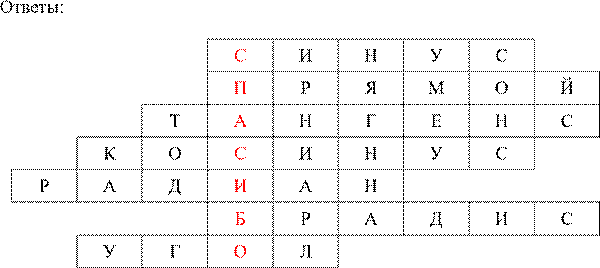
Приложение 1

2. Угол, синус которого равен единице, а косинус – нулю.

3. Тригонометрическая функция, область значений которой – вся числовая прямая.

4. Название четной тригонометрической функции.

5. Единица измерения угла.

6. Составитель четырехзначных таблиц.

7. Смысл приставки “arc-“

Министерство науки и образования

Учебный предмет: ОУП 04 Математика

Личностные: - развитие самостоятельного мышления в учебной деятельности, навыков самоконтроля; - развитие логического мышления, алгоритмической культуры и интуиции, творческих способностей на уровне, необходимом для продолжения…

Этап, время Деятельность

Вспомнить основные формулы решения тригонометрических уравнений, чтобы не допускать ошибо при решении тригонометрических уравнений

Постановка цели урока. 2 мин

Z 6 в) 2cos x  3 3 cos x  2  3  x  arccos  2  k ; k 

Z x     k ; k  Z 6

Воспроизведе Самостоятельная работа :

Вариант 1 2 1) cos x  2 2) 2cos x  3  0 3) 2sin x  1  0 4) tgx …

Z 4 самостоятельную работу,