МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИЗУЧЕНИЯ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ В КУРСЕ МАТЕМАТИКИ СРЕДНЕЙ ШКОЛЫ

ВВЕДЕНИЕ

Данный курс представляет собой большой интерес в плане практического применения на практике в школе. Большое значение в этом направлении имеют формулы сокращенного умножения и их методические особенности, что обуславливает выбор темы курсовой работы. В ходе работы были рассмотрены вопросы школьной и внешкольной программы, а также исторические сведения по теме. Эта тема значимая в курсе математики и применяется на протяжении всего периода обучения: при умножении многочленов, упрощении алгебраических выражений, сокращении дробей, разложении на множители, решении уравнений и так далее.

Изучение различных преобразований выражений и формул занимает значительную часть учебного времени в курсе школьной математики. Простейшие преобразования, опирающиеся на свойства арифметических операций, производятся уже в начальной школе и в IV–V классах. Но основную нагрузку по формированию умений и навыков выполнения преобразований несет на себе курс школьной алгебры. Это связано как с резким увеличением числа и разнообразия совершаемых преобразований, так и с усложнением деятельности по их обоснованию и выяснению условий применимости, с выделением и изучением обобщенных понятий тождества, тождественного преобразования, равносильного преобразования, логического следования.

Цель данной работы: изучение различных приложений формул сокращенного умножения в курсе математики средней школы. Для того, чтобы достичь сформулированную цель исследования поставлены следующие задачи:

1) анализ и систематизация основных теоретических сведений, касающихся темы исследования;

2) изучение формул сокращенного умножения.

3) анализ методико-математической литературы и выявление приемов введения и формирования понятия формул сокращенного умножения на уроках математики.

ГЛАВА 1 МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИЗУЧЕНИЯ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ В КУРСЕ МАТЕМАТИКИ СРЕДНЕЙ ШКОЛЫ

1.1 Формирование навыков применения конкретных видов преобразований

Система приемов и правил проведения преобразований, используемая на этапе начал алгебры, имеет очень широкую область приложений: она используется в изучении всего курса математики. Однако именно в силу своей малой специфичности эта система нуждается в дополнительных преобразованиях, учитывающих особенности структуры преобразуемых выражений и свойства вновь вводимых операций и функций. Освоение соответствующих видов преобразований начинается с введения формул сокращенного умножения. Затем рассматриваются преобразования, связанные с операцией возведения в степень, с различными классами элементарных функций – показательных, степенных, логарифмических, тригонометрических. Каждый из этих типов преобразований проходит этап изучения, на котором внимание сосредоточивается на усвоении их характерных особенностей.

Преобразования разделяются на два класса: тождественные преобразования – это преобразования выражений, и равносильные – преобразования формул. В случае, когда возникает потребность в упрощении одной части формулы, в этой формуле выделяется выражение, которое и служит аргументом применяемого тождественного преобразования. Соответствующий предикат при этом считается неизменным.

В курсе алгебры и начал анализа целостная система преобразований, в основных чертах уже сформированная, продолжает постепенно совершенствоваться. К ней также добавляются некоторые новые виды преобразований, однако они только обогащают ее, расширяют ее возможности, но не меняют ее структуру. Методика изучения этих новых преобразований практически не отличается от применяемой в курсе алгебры.

1.2 Особенности организации системы заданий при изучении тождественных преобразований

Основной принцип организации любой системы заданий – предъявление их от простого к сложному, с учетом необходимости преодоления учениками посильных трудностей и создания проблемных ситуаций. Указанный основной принцип требует конкретизации применительно к особенностям данного учебного материала. Для описания различных систем заданий в методике математики используется понятие цикла упражнений. Цикл упражнений характеризуется соединением в последовательности упражнений нескольких аспектов изучения и приемов расположения материала. По отношению к тождественным преобразованиям представление о цикле может быть дано следующим образом.

Цикл упражнений связан с изучением одного тождества, вокруг которого группируются другие тождества, находящиеся с ним в естественной связи. В состав цикла, наряду с исполнительными, входят задания, требующие распознавания применимости рассматриваемого тождества. Изучаемое тождество применяется для проведения вычислений на различных числовых областях. Учитывается специфика тождества; в частности, организуются связанные с ним обороты речи. Задания в каждом цикле разбиты на две группы. К первой относятся задания, выполняемые при первоначальном знакомстве с тождеством. Они служат учебным материалом для нескольких идущих подряд уроков, объединенных одной темой. Вторая группа упражнений связывает изучаемое тождество с различными приложениями. Эта группа не образует композиционного единства – упражнения здесь разбросаны по различным темам.

Описанная структура цикла относится к этапу формирования навыков применения конкретных видов преобразований. На заключительном этапе – этапе синтеза циклы видоизменяются. Во-первых, объединяются обе группы заданий, образующие «развернутый» цикл, причем из первой группы исключаются наиболее простые по формулировкам или по сложности выполнения задания. Оставшиеся типы заданий усложняются. Во-вторых, происходит слияние циклов, относящихся к различным тождествам, в силу чего повышается роль действий по распознаванию применимости того или иного тождества.

Описанная структура цикла относится к этапу формирования навыков применения конкретных видов преобразований. На заключительном этапе – этапе синтеза циклы видоизменяются. Во-первых, объединяются обе группы заданий, образующие «развернутый» цикл, причем из первой группы исключаются наиболее простые по формулировкам или по сложности выполнения задания. Оставшиеся типы заданий усложняются. Во-вторых, происходит слияние циклов, относящихся к различным тождествам, в силу чего повышается роль действий по распознаванию применимости того или иного тождества.

Значительная часть тождеств, изучаемых в курсах алгебры и алгебры и начал анализа, доказывается в них или, по крайней мере, поясняется. Эта сторона изучения тождеств имеет большое значение для обоих курсов, поскольку доказательные рассуждения в них с наибольшей четкостью и строгостью проводятся именно по отношению к тождествам. За пределами этого материала доказательства обычно менее полны, они не всегда выделяются из состава применяемых средств обоснования.

В качестве опоры, на которой строятся доказательства тождеств, используются свойства арифметических операций. Воспитательное воздействие вычислений и тождественных преобразований может быть, направлено на развитие логического мышления, если только от учащихся будут систематически требоваться обоснования вычислений и тождественных преобразований, на развитие функционального мышления, что достигается различными путями. Совершенно очевидно значение вычислений и тождественных преобразований в развитии воли, памяти, сообразительности, самоконтроля, творческой инициативы.

1.3 Методика работы с формулами сокращенного умножения

Целью преподавания математики в школе является сообщение учащимся фактических знаний в области математики и воспитание у них необходимых умений для применения полученных знаний в различных практических вопросах. Одновременно преподавание математики служит образовательным и воспитательным целям. Успешное понимание того, что объясняется на уроках, во многом зависит от того, как подготовлены учащиеся к восприятию нового материала. Подготовка во многом обеспечивает успех учебного процесса, поэтому каждый урок должен строиться так, чтобы на нем не только закреплялся и углублялся пройденный материал и на его базе изучался новый, но и создавалась база для успешного изучения материала будущих уроков.

Культура выполнения тождественных преобразований развивается так же, как и культура вычислений, на основе прочных знаний свойств операций над объектами (числами, векторами, многочленами и т. д.) и алгоритмов их выполнения. Она проявляется не только в умении правильно обосновать преобразования, но и в умении найти кратчайший путь перехода от исходного аналитического выражения к выражению, наиболее соответствующему цели преобразования, в умении проследить за изменением области определения аналитических выражений в цепочке тождественных преобразований, в быстроте и безошибочности выполнения преобразований. Обеспечение высокой культуры вычислений и тождественных преобразований представляет важную проблему обучения математике. Однако эта проблема решается еще далеко не удовлетворительно. Доказательство этому – статистические данные органов народного образования, в которых ежегодно констатируются ошибки и нерациональные приемы вычислений и преобразований, допускаемые учащимися различных классов при выполнении контрольных работ.

Знакомство учащихся с формулами сокращенного умножения  происходит, как правило, в-седьмом классе. Затем понятия формул сокращенного умножения уточняется и расширяется в старших классах. В связи с этим учителю необходимо знать правила выполнения действий над формулами сокращенного умножения. Все это нужно не только для того чтобы математически грамотно ввести понятие формул сокращенного умножения и обучать школьников выполнять с ними действия, но и, что не менее важно, видеть взаимосвязи с различными преобразованиями. Без их понимания нельзя решить проблему преемственности в обучении математике в средних школах.

Формулы сокращенного умножения важны в алгебре, широко используются в алгебраических вычислениях, в рациональных расчетах при решении задач. Для их качественного усвоения от детей требуется значительные умственные, волевые усилия, напряжение. Для этого нужно поддерживать интерес к исследовательским, развивающим, тренировочным упражнениям по «открытию» формул, их осмысленному использованию. Можно считать, что успеху содействует урок, на котором ребята поставлены в условия живой исследовательской групповой работы, математической игры и творчества. . Сами формулы представляются ребятам как результат усердия, их открытия. В процесс, в «таинства» алгебраических открытий, что очень важно, вовлекаются и «слабые» ученики – это развивает их математические способности, помогает выработке умений и навыков.

Тема «Формулы сокращенного умножения» является основополагающей в разделе «Тождественные преобразования алгебраических выражений». Поэтому важно, чтобы ученики автоматически применяли их не только при решении примеров, но и при выполнении других заданий: таких, как решение уравнений, преобразование выражений, доказательство тождеств.

Для изучения темы «Формулы сокращенного умножения. Квадрат суммы и квадрат разности» в седьмом классе выделяется пять часов. Для темы «Разность квадратов. Сумма и разность кубов» выделяют шесть часов на ее изучение.

Представим в виде таблицы в каком порядке идет изучение данной темы, а так же что ученики должны знать:

Урок, на котором разъясняется вывод формул сокращенного умножения, стоит начать с устных заданий. Они будут служить итогом подготовительных упражнений, предлагавшихся школьникам на предыдущих уроках. После устных упражнений классу нужно сообщить учебную задачу. Ученикам предлагается быть в роле исследователей и «открыть» несколько формул сокращенного умножения.

На следующих уроках учащиеся вспоминают формулы сокращенного умножения. Стоит обратить внимание на словестные формулировки формул. Фронтально можно провести устные тренировочные упражнения (5 мин), цель которых – развитие зрительного восприятия, быстрого узнавания формул и их выражений. По активности детей и количеству допущенных ошибок, недочетов учитель оценивает готовность класса к решению более сложных письменных упражнений.

Далее решаются примеры по учебнику. Первые 2 – 3 примера решаются с объяснением на доске. Затем дети решают аналогичные примеры самостоятельно. Учитель в это время ведет наблюдение и контролирует отдельных учеников. Очень важно, чтобы ребята увидели и поняли значение формул для упрощения, рационализации вычислений.

С каждым уроком примеры усложняются. Решаются уравнения, преобразовываются выражения, доказываются тождества. В конце урока ребятам можно дать самостоятельную работу(15 мин). Задания дифференцируются. Цель работы – проверить умения и навыки применения формул. 15-минутная программированная самостоятельная работа по данной теме является итоговой и служит основанием для оценки знаний, умений и навыков учащихся.

1.4 Квадрат суммы и квадрат разности

Можем рассмотреть , как с помощью некоторых формул можно упрощать преобразования при умножении многочленов.

Теорема 1. При любых значениях a и b верно равенство:

.                       (1)

Доказательство.

Так как равенство (1) верно при любых значениях a и b , то оно является тождеством. Это тождество называется формулой квадрата суммы и читается так:

квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

Эта формулировка показана в виде схемы (Рис. 1):

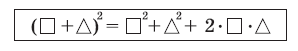
Рис.1

Так же можно представить данную схему в виде геометрической иллюстрации формулы (Рис. 2):

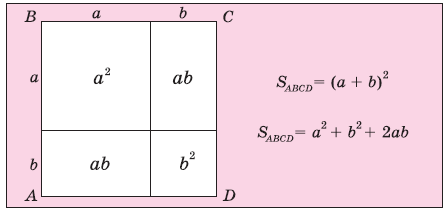
Рис. 2

Теорема 2. При любых значениях a и b верно равенство:

.                       (2)

Так как равенство (2) верно при любых значениях, то оно является тождеством. Это тождество называется формулой квадрата разности и читается так:

квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

Эта формулировка показана в виде схемы (Рис. 3):

Рис. 3

Рассмотрим пару примеров с использованием формул квадрата суммы и разности:

Пример 1. Вычислить значение выражения, применив формулу квадрата суммы или разности:

а) ;

б) .

Решение.

а);

б)

Пример 2. Преобразовать выражение в многочлен стандартного вида:

Решение.

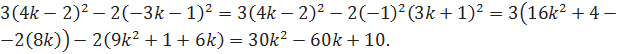
1.5 Разность квадратов

Теорема 1. При любых значениях a и b верно равенство:

.                       (3)

Доказательство.

.

Так как равенство (3) верно при любых значениях a и b, то оно является тождеством. Это тождество называется формулой разности квадратов. Если в эту формулу вместо a и b подставить какие-нибудь выражения, то опять получится тождество. Формула разности квадратов читается так:

произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Эта формулировка показана в виде схемы (Рис. 4):

Рис. 4

Пример 1. Упростить выражение , применив формулу разности квадратов.

Решение.

Пример 2. Упростить выражение , применив формулу разности квадратов.

Решение.

1.6 Куб суммы и куб разности

Теорема 1. При любых значениях a и b верно равенство:

          (4)

Так как равенство (4) верно при любых значениях a и b, то оно является тождеством. Это тождество называется формулой куба суммы. Если в эту формулу вместо a и b подставить какие-нибудь выражения, то опять получится тождество. Формула куба суммы читается так:

куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго, плюс утроенное произведение первого выражения и квадрата второго, плюс куб второго выражения.

Эта формулировка показана в виде схемы (Рис. 5):

Рис. 5

Теорема 2. При любых значениях a и b верно равенство:

          (5)

Так как равенство (5) верно при любых значениях a и b, то оно является тождеством. Это тождество называется формулой куба разности. Если в эту формулу вместо a и b подставить какие-нибудь выражения, то опять получится тождество. Формула куба разности читается так:

куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго, плюс утроенное произведение первого выражения и квадрата второго, минус куб второго выражения.

Эта формулировка показана в виде схемы (Рис. 6):

Рис. 6

1.7 Сумма кубов и разность кубов

Теорема 1. При любых значениях a и b верно равенство:

           (6)

Так как равенство (6) верно при любых значениях a и b, то оно является тождеством. Это тождество называется формулой суммы кубов. Если в эту формулу вместо a и b подставить какие-нибудь выражения, то опять получится тождество. Формула суммы кубов читается так:

произведение суммы двух выражений и неполного квадрата и их разности равно сумме кубов этих выражений.

Эта формулировка показана в виде схемы (Рис. 7):

Рис. 7

Теорема 2. При любых значениях a и b верно равенство:

           (7)

Так как равенство (7) верно при любых значениях a и b, то оно является тождеством. Это тождество называется формулой разности кубов. Если в эту формулу вместо a и b подставить какие-нибудь выражения, то опять получится тождество. Формула разности кубов читается так:

произведение разности двух выражений и неполного квадрата и их суммы равно разности кубов этих выражений.

Эта формулировка показана в виде схемы (Рис. 8):

Рис. 8

ГЛАВА 2 РАЗЛИЧНЫЕ ПРИЛОЖЕНИЯ ФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ В КУРСЕ МАТЕМАТИКИ СРЕДНЕЙ ШКОЛЫ

2.1 Приложения формул сокращенного умножения при преобразовании алгебраических выражений

Пример 1. Преобразовать выражение  в многочлен стандартного вида:

Решение.

.

Ответ: .

Пример 2. Преобразовать выражение  в многочлен стандартного вида:

Решение.

.

Ответ: .

Пример 3. Преобразовать выражение  в многочлен стандартного вида:

Решение.

.

Ответ: .

Пример 4. Преобразовать выражение  в многочлен стандартного вида:

Решение.

Ответ: .

Пример 5. Преобразовать выражение  в многочлен стандартного вида:

Решение.

.

Ответ: .

Пример 6. Представить выражение в виде многочлена стандартного вида:

Решение.

.

Ответ:.

Пример 7. Представить выражение  в виде многочлена стандартного вида:

Решение.

.

Ответ: .

2.2 Применение формул сокращенного умножения при решении уравнений

Пример 1. Решить уравнение, используя формулы сокращенного умножения:

.

Решение.

Ответ:

Пример 2. Решить уравнение, используя формулы сокращенного умножения:

Решение.

Ответ:

Пример 3. Решить уравнение, используя формулы сокращенного умножения:

Решение.

Ответ:

Пример 4. Решить уравнение, используя формулы сокращенного умножения:

Решение.

Ответ:

Пример 5. Решить уравнение, используя формулы сокращенного умножения:

Решение.

Ответ:

Пример 6. Решить уравнение, используя формулы сокращенного умножения:

Решение.

Ответ:

Пример 7. Решить уравнение, используя формулы сокращенного умножения:

Решение.

Ответ:

Пример 8. Решить уравнение, используя формулы сокращенного умножения:

Решение.

;

;

Ответ:

Пример 9. Решить уравнение, используя формулы сокращенного умножения:

Решение.

Ответ:

Пример 10. Решить уравнение, используя формулы сокращенного умножения:

Решение.

Ответ:

Пример 11. Решить уравнение, используя формулы сокращенного умножения:

Решение.

.

Ответ:

2.3 Применение формул сокращенного умножения при нахождении значений выражений

Пример 1. Найти значение выражения:

, при  ,

Решение.

Ответ: 64.

Пример 2. Найти значение выражения:

 при  m=.

Решение.

*=49.

Ответ: 49.

Пример 3. Найти значение выражения:

 при

Решение.

=

Ответ: 8.

Пример 4. Найти значение выражения:

 при

Решение.

  =

Ответ: 64.

Пример 5. Найти значение выражения:

Решение.

=

Ответ:

Пример 6. Найти значение выражения:

Решение.

Ответ: 26.

Пример 7. Найти значение выражения:

Решение.

Ответ: 21.

Пример 8. Найти значение выражения:

Решение.

Ответ: 113.

Пример 9. Найти значение выражения:

Решение.

Ответ: 46.

2.4 Применение формул сокращенного умножения при доказательстве тождеств

Пример 1. Докажите тождество:

Решение.

Ответ: тождество доказано.

Пример 2. Докажите тождество:

Решение.

Ответ: тождество доказано.

Пример 3. Докажите тождество:

Решение.

+

Ответ: тождество доказано.

Пример 4. Докажите тождество:

Решение.

Ответ: тождество доказано.

Пример 5. Докажите тождество:

Решение

Ответ: тождество доказано.

Пример 5. Докажите тождество:

Решение

Ответ: тождество доказано.

2.5 Применение формул сокращенного умножения при решении задач повышенной трудности

Задача 1. Докажите, что  кратно 24, если  – простое число, больше 3.

Доказательство.  Так как 24=3*8, где 3 и 8 – взаимно простые числа, то для доказательства делимости  на 24 достаточно доказать его делимость: а) на 3, б) на 8.

а) Для доказательства делимости на 3 рассмотрим три последовательных натуральных числа:  Так как из трех последовательных натуральных чисел одно всегда делится на 3, а  – число простое и больше 3(по условию), то на 3 делится одно из чисел: . Следовательно,  делится на 3.

Замечание. Доказать делимость  на 3 можно методом полной индукции(что можно рассмотреть на дополнительных занятиях).

б) Так как  простое, больше 3, то  – число нечетное. Следовательно,  – числа четные. Пусть , тогда

.

Так как из двух последовательных натуральных чисел одно число четное, то число , равное , делится на 8. Следовательно,  делится на 24. Утверждение доказано.

Задача 2. При каких значениях  равенство

 является тождеством?

Решение. Раскроем скобки в правой части равенства и приведем подобные члены:

Для того, чтобы равенство

было тождеством, необходимо, чтобы коэффициенты при одинаковых степенях совпадали. Приравнивая их, получим систему уравнений:

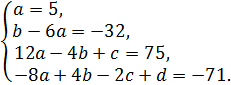
Решив ее, получим, что при данное равенство будет тождеством.

Ответ:

Задача 3. Представьте многочлен  в виде многочлена

Решение. 1 способ. Из равенства  выразим  и подставим значение  в данный многочлен:

Ответ:

2 способ. Необходимо найти такие значения a, b, с и d, чтобы равенство

являлось тождеством.

Решаем способом, применимым при решении предыдущей задачи:

Получили

Имеем систему уравнений:

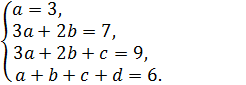
откуда

Ответ:

Задача 4. У школьника было несколько монет достоинством в 15 к. и 20 к., причем двадцатикопеечных монет было больше, чем пятнадцатикопеечных. Пятую часть всех денег школьник истратил, отдав две монеты за билеты в кино. Половину оставшихся денег он отдал за обед, оплатив его тремя монетами. Сколько монет каждого достоинства было у школьника вначале?

Решение. Задача сводится к решению в натуральных числах уравнения 20x+15y = n,  где х — число двадцатикопеечных монет, у — число пятнадцатикопеечных монет, причем х>у; натуральное число п определяется из условия задачи.

Так как пятая часть всех денег была уплачена двумя монетами, то пятая часть денег равна либо 40 к. (две монеты по 20 к.), либо 30 к. (две монеты по 15 к.), либо 35 к. (20к. + 15 к.). Тогда всего денег у школьника было либо 200 к., либо 150 к., либо 175 к. Половина оставшихся после кино денег либо 80 к. , либо 60 к. ,, либо 70 к.( .

Легко установить, что половина оставшихся денег составляет 60 к. (70 к. и 80 к. нельзя оплатить тремя монетами достоинством в 15 к. и 20 к.), а все деньги — 150 к.

Решая уравнение 20x+15y = 150 при x>y в натуральных числах, найдем

x= 6, y = 2.

Ответ: x= 6, y = 2.

Задача 5. Если то значение выражения

положительно. Докажите.

Доказательство. Преобразуем данное выражение:

При данном условии и при  каждое слагаемое полученной суммы положительно. При a=b второе слагаемое , при a= - b первое слагаемое . Таким образом, в любом случае выражение положительно. Утверждение доказано.

Задача 6. Докажите, что уравнение не имеет  решений в целых числах (т. е. когда х и у оба целые).

Доказательство. Разложив левую и правую часть уравнения на множители, будем  — целые числа, в произведении дающие 30 .Из уравнения следует система

откуда  — число четное, а число , в чем легко убедиться перебором,— число нечетное. Следовательно, данное уравнение не имеет решения в целых числах.

Ответ: уравнение не имеет решения в целых числах.

Задача 7. Докажите, что не существует целых коэффициентов  таких, что значение многочлена  равно 1 при  и равно 2 при .

Доказательство. Допустим, что существуют такие коэффициенты , что верны равенства

Вычтя из второго равенства первое, будем иметь:

oткуда

При целых а, Ь и с в левой части последнего равенства получим целое число (а не ) . Пришли к противоречию.

Задача 8. Найдите все простые числа , для которых

Решение. Из равенства  имеем откуда . Так как в правой части равенства имеем произведение равных простых чисел ( не имеет других делителей, кроме  и 1), то и в левой части равенства имеем произведение равных чисел, т. е. , откуда

 = 3. Следовательно,

Ответ:

Задача 9. Представьте выражение 24xy в виде разности квадратов двух многочленов.

Решение. Представим выражение 24xy  в виде суммы двух тождественно равных одночленов:

Затем одночлен  представим как удвоенное произведение одного числа на другое. Будем иметь:

Замечание. Целесообразно доказать, что задача имеет бесконечное множество решений. Действительно,  , где a— любое действительное число, не равное нулю.

Тогда

.

Задача 10. Представьте выражение  в виде суммы кубов двух многочленов.

Решение.

Ответ: .

Задача 11. Представьте выражение  в виде разности кубов двух многочленов.

Решение.

Ответ:

ЗАКЛЮЧЕНИЕ

Тема формул сокращенного умножения, в общем, является одной из часто используемых в вычислениях и решении различных задач. Поэтому о преобразованиях и формулах сокращенного умножения начинают говорить уже с начала средней школы при изучении математики. В работе были приведены задания, разные по сложности и по содержанию, с использованием формул сокращенного умножения. Данные задания могут быть использованы для проведения контрольных или самостоятельных работ проверки знаний учащихся

Учителю необходимо владеть формулами сокращенного умножения, знать правила выполнения действий над формулами сокращенного умножения, не только для того, чтобы математически грамотно ввести понятие формул и обучать школьников выполнять действия, но и, что не менее важно, видеть взаимосвязи формул с тождествами, уравнениями и различными преобразованиями. Осваивая формулы, учащиеся должны поупражняться в решении примеров, уравнений и преобразовании тождеств.

Целью данной работы было: изучение различных приложений формул сокращенного умножения в курсе математики средней школы. Для того, чтобы достичь сформулированную цель исследования были поставлены и выполнены следующие задачи:

1) анализ и систематизация основных теоретических сведений, касающихся темы исследования;

2) изучение формул сокращенного умножения.

3) анализ методико-математической литературы и выявление приемов введения и формирования понятия формул сокращенного умножения на уроках математики.

Поставленная цель исследования была достигнута по средствам решения сформулированных задач, что позволило раскрыть тему курсовой работы. Курсовая работа выполнена в рамках методики преподавания математики в средне образовательных учреждениях.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Азаров А. И. Математика 100 баллов успеха / А. И. Азаров. 2-е. изд. – Минск: Аверсэв, 2017. – 639 с.

2. Арефьева, И. Г. Математика. Пособие репетитор / И. Г. Арефьева. 4-е. изд. – Минск: Аверсэв, 2015. – 750 с.

3. Бунимович, Е. А. Математика. Рабочая тетрадь. 6 класс / Е.А. Бунимович, Л. В. Кузнецова, Л. О. Рослова; под ред. Е. А. Бунимовича. – Москва: Просвещение,  2014. – 239 с.

4. Виленкин, Н. Я. Математика. Учебник для 6 кл. / Н.Я. Виленкин, В. И. Жохов, А. С. Чесноков; под ред. Н. Я. Виленкин. – Москва: Просвещение,  2006. – 169 с.

5. Дорофеев, Г. В. Математика 6 класс / Г.В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова; под ред. Г. В. Дорофеев. – Москва: Просвещение,  2013. – 353 с.

6. Дорофеев, Г. В. Алгебра 7 класс / Г.В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова; под ред. Г. В. Дорофеев. – Москва: Просвещение,  2013. – 321 с.

7. Кузнецова Е. П. Математика. Учебник для 6 кл. / Е. П. Кузнецова, Г. Л. Муравьёва, Л. Б. Шнеперман; под ред. Л. Б. Шнепермана. – Минск: Нац. Ин-т образования, 2014. – 328 с.

8. Кузнецова, Л. В. Математика. Дидактические материалы. 7 класс / Л.В. Кузнецова, С. С. Минаева, Л. О. Рослова; под ред. Л. В. Кузнецова. – Москва: Просвещение,  2014. – 139 с.

9. Латонин, Л. А. Математика 6 кл / Л. А. Латонин. 4-е изд. Миснк: Народная асвета, 2014. – 318 с.

10. Никольский, С. М. Арифметика. Учебник для 7 кл. / С.М. Никольский, М. К. Решетников, Н. Н. Шевкин; под ред. С. М. Никольский. – Москва: Просвещение, 2006. – 191 с.