Методические указания для решения текстовых задач

Методические указания для решения текстовых задач для слабослышащих

Обучение нацелено на формирование умения решать задачи определенных типов. При решении этих задач у учащихся с нарушением слуха формируется и закрепляется понятие об использовании тех или иных арифметических действиях в задачах. Они учатся решать сначала простые задачи, а затем составные, включающие в себя различные сочетания простых задач.

Важно научить слабослышащих детей выполнять семантический и математический анализ текстовых задач, выявлять взаимосвязи между условием и вопросом, данными и искомыми, представлять эти связи в виде схематических и символических моделей. Процесс решения рассматривается как переход от словесной модели к модели математической или схематической. Этот подход сориентирован на формирование обобщенных умений: читать задачу, выделять условие и вопрос, устанавливать взаимосвязь между ними, осознанно использовать математические понятия при выборе арифметических действий для ответа на вопрос задачи. До знакомства с решением задачи проводится специальная работа, направленная на усвоение учащимися понятий и отношений, используемых при решении текстовых задач (А.В.Белошистая, Н.Б.Истомина и др.).

Для формирования умения решать задачи П. М. Эрдниев предлагает использовать метод взаимообратных задач. К примеру, находят решение предложенной задачи, затем составляют 2 взаимообратные задачи к данной и т. д.

В методической литературе [2] указывается, что необходимо проводить подготовительную работу перед решением задач. Учащиеся должны усвоить:

- отношения, связи и зависимости между величинами, на основе которых выбираются действия, необходимые для решения задачи;

- смысл арифметических действий;

- связь отношений «больше (меньше) на...», «больше (меньше) в...» с арифметическими действиями;

- связи между компонентами и результатом действия;

- умение переводить эти связи на язык математических отношений и зависимостей, осознанно выбирать действия.

По мнению Н.Б.Истоминой [8], готовность учащихся к знакомству с текстовой задачей предполагает сформированность:

- навыков чтения;

- представлений о смысле арифметических действий, их взаимосвязи, понятий «увеличить (уменьшить) на ...», разностного сравнения (для этих целей следует использовать не решения простых задач, а соотнесение предметных, вербальных, графических, схематических и символических моделей);

- основных мыслительных операций (анализ, синтез, сравнение, обобщение);

- умения описывать предметные ситуации и переводить их на язык схем и математических символов;

- умения чертить, складывать и вычитать отрезки;

- умения переводить текстовые ситуации в предметные и схематические модели.

Одной из важных задач обучения, стоящих перед учителем, является формирование у учащихся с нарушением слуха общего умения решать арифметические задачи.

Умение решать задачи представляет собой сложное умение, включающее в себя ряд последовательно связанных частных умений:

- прочитать задачу и представить ту ситуацию, которая в ней описана;

- выделить условие и вопрос (требование) задачи, известные и неизвестные значения величин;

- установить связи и зависимости между величинами, входящими в задачу;

- перевести зависимости между данными и искомыми на язык математических символов (выражений, уравнений, равенств);

- составить план решения;

- выполнить решение задачи;

- проверить решение и записать ответ.

Обучение решению задач дает возможность работать над каждым из этих частных умений в отдельности и над их комплексным использованием в процессе решения задачи. При этом усваивается общий подход к решению любых задач (М.И.Моро).

Рассматривая вопрос использования текстовых задач в обучении математике, М. И. Моро отмечает, что целью работы над задачами вовсе не является разучивание с учащимися способов решения задач определенных типов. Цель состоит в том, чтобы обеспечить лучшее усвоение включенных в программу вопросов теории, научить применять теоретические знания на практике и развивать мышление учащихся.

В своих работах Ю. М. Колягин указывает, что не надо разучивать алгоритмы решения задач того или иного типа, но и не следует отказываться от обобщения решения нескольких задач в тот или иной метод (алгоритм, правило) решения задач определенного типа, так как каждый тип задач имеет свои особенности. Неслучайно почти во всех учебниках математики для начальной школы выделяются группы задач, например, задачи на движение (группа задач выделена по сюжету) и др.

В процессе работы над задачей можно выделить следующие этапы: ознакомление с содержанием задачи; поиск пути решения (разбор задачи), выполнение решения задачи; проверка и запись ответа.

При обучении решению текстовых задач необходимо стремиться к тому, чтобы слабослышащие учащиеся отдавали себе отчет в возможности различных способов решения и сознательно выбирали наиболее рациональный из них. Поэтому решению задач различными способами в практике обучения необходимо уделять больше внимания.

Умение решать задачу различными способами связывается с развитием гибкости мышления и играет определенную роль в развитии умственных способностей и математического мышления. Обучение решению задач различными способами способствует более глубокому осознанию задачной ситуации, пониманию взаимосвязей между величинами, входящими в задачу, между данными и искомыми, развивает наблюдательность и математическую зоркость. В методической литературе отмечается, что решение задачи различными способами часто бывает более полезным, чем решение одним способом нескольких задач. При оценке разных способов решения активно используются такие умственные операции, как анализ, синтез, сравнение, обобщение, что оказывает положительное влияние на развитие умственных способностей учащихся.

В методической литературе выделяют арифметические и алгебраические методы решения задач. Кроме этих основных методов можно указать еще графический, практический, табличный, логический и смешанный.

Арифметический метод решения задачи основан на выборе арифметических действий, обусловленном различными связями и зависимостями между величинами, входящими в задачу, между данными и искомыми. В зависимости от выбора величин и последовательности их выбора можно решить задачу несколькими способами. Способы решения отличаются друг от друга хотя бы одним или несколькими действиями.

Например, дана задача: «Для похода туристы закупили 96 банок консервов. В день они расходовали по 8 банок. Сколько банок консервов у них осталось после 10 дней?» Задача может быть решена двумя способами.

1-й способ:

1) 8-10=80 (б.);

2) 96-80=16 (б.).

2-й способ:

1) 96:8=12 (дн.);

2) 12-10=2 (дн.);

3) 8-2=16(б.).

Сопоставив рассмотренные способы решения задачи, нетрудно заметить, что 1-й способ рациональный.

Алгебраические способы решения задач основаны на общем методе, заключающемся в установлении неизвестного, обозначении его буквой и введении его в текст задачи. Затем на основе выделенных зависимостей между величинами составляют два выражения, которые связаны отношением равенства, что позволяет записать уравнение или систему уравнений. Таким образом, текст задачи переводят на язык математики, составляют математическую модель задачи. В зависимости от выбора неизвестного и от хода рассуждений можно составить несколько уравнений к одной и той же задаче, т. е. решить задачу несколькими алгебраическими способами.

Например, дана задача: «Из двух пунктов одновременно навстречу друг другу вышли два лыжника и через 2 ч встретились. Найдите скорость каждого лыжника, если расстояние между пунктами было 44 км, а скорость одного больше скорости другого на 2 км/ч».

Пусть х км/ч — скорость первого лыжника, тогда скорость второго — х + 2 км/ч. Расстояние, пройденное первым лыжником за 2 ч, — 2 - х км, а вторым — (х + 2)·2 км. По условию задачи, расстояние между пунктами равно 44 км.

Составляем уравнение: 2 – х + (х + 2) · 2 = 44.

Отсюда 4 – х = 40, х= 10.

Ответ: скорость первого лыжника — 10 км/ч, скорость второго — 10 + 2 = 12 (км/ч).

По условию задачи можно составить второе уравнение:

(х - 2)·2 + 2х = 44 .

Отсюда: 4х = 4 + 44; 4х = 48 ; х = 12.

Ответ: скорость второго лыжника – 12 км/ч, скорость первого – 12 - 2 = = 10 (км/ч).

Таким образом, задача решена двумя алгебраическими способами.

Практический метод решения задачи заключается в выполнении действий над предметными множествами, иллюстрирующими задачную ситуацию, а для ответа на вопрос арифметическое действие можно не выполнять. Например, дана задача: «8 яблок разложили на две тарелки. Поскольку яблок на каждой тарелке?» Эту задачу в 1 классе учащиеся могут решить только практически: берут рисунки с изображением яблок (или кружки) и раскладывают на тарелки. Ответ на вопрос находят путем пересчета яблок на каждой тарелке. Использование этого метода целесообразно лишь в случае, когда выполняются действия над небольшим количеством предметных множеств, иллюстрирующих задачу.

Графический метод решения задач представляет собой построение чертежа, позволяющего дать ответ на вопрос задачи без выполнения арифметического действия. Например, дана задача: «Масса арбуза — 5 кг, а масса дыни на 2 кг меньше. Какова масса дыни?»

Изобразим числовые данные в виде отрезков (рис. 3).

Рис. 1. Отрезки

Ответ на вопрос можно дать, пересчитав отрезки или измерив полученный отрезок. Решение задачи графическим способом дает возможность усилить ее обучающую функцию, кроме того, служит способом проверки решения задачи арифметическим способом. Иногда решение задачи графическим способом связано не только с построением отрезков, но и с их измерением.

В методической литературе [2] отмечается, что почти любую арифметическую задачу, которую решают в 1 классе, можно решить графически без выполнения арифметических действий. При этом учащиеся могут убедиться, что иногда этот подход к решению задач приводит к усложнению, а иногда позволяет легко и просто решить задачу.

Табличный метод решения задач — это метод произвольного допущения. Он дает возможность показать предельно четкое и ясное решение некоторых задач, представляющих немалую трудность. Например, дана задача: «В парке посадили 40 деревьев, причем на каждую липу приходилось 4 клена. Сколько лип и сколько кленов было посажено в парке?» Решение задачи записывается в таблице (табл. 1).

Таблица 1

Заполнив таблицу, обращают внимание на число, данное в условии задачи, — всего 40 деревьев, значение чисел в соответствующих колонках дают ответ на вопрос задачи. Логический метод решения задачи состоит в том, что в процессе поиска решения на основе логических рассуждений можно дать ответ на вопрос задачи. Смешанный способ решения задачи предполагает использование приемов работы по решению задач различными способами:

- беседа, в процессе которой учитель подводит учащихся к тому или иному способу решения задачи;

- обсуждение готовых решений — на доске учитель предлагает учащимся разные способы решения задачи и дает задание объяснить каждое выполняемое действие.

Поясним сказанное на примере задачи: «Рабочему было поручено изготовить 30 одинаковых деталей за 10 ч. Но рабочий, экономя время, успевал делать одну деталь за 15 мин. Сколько деталей сверх задания сделал рабочий за счет сэкономленного времени?» В процессе беседы учитель, обратив внимание учащихся на соотношение единиц времени (10 ч = 600 мин), может привести их к указанным далее способам решения задачи или предложить готовые решения, а учащиеся должны объяснить каждое решение, сравнить разные способы и установить, какой из них оказался наиболее легким, рациональным.

1-й способ:

1) 600:30=20 (мин);

2)20-15=5 (мин);

3) 5-30=150 (мин);

4) 150:15=10 (дет.).

2-й способ:

1) 15-30=450 (мин);

2) 600-450=150 (мин);

3) 150:15=10 (дет.).

3-й способ:

1) 60:15=4 (дет.);

2) 4-10=40 (дет.);

3) 40-30=10 (дет.).

4-й способ:

1)600:15=40 (дет.);

2) 40-30=10 (дет.).

Учитель также может предложить продолжить начатое решение, например: 1) 600:30=20; 2) 20-...= 5; 3) 5-... = 150; 4) ... : ... = 10.

Возможно решение задачи по предложенному плану. Например, учитель предлагает план решения задачи, а учащиеся должны подобрать действие к каждому пункту плана:

- найдите время, затраченное на изготовление деталей (15-30=450);

- найдите сэкономленное время (600 - 450 = 150);

- найдите число деталей, которые рабочий сделал сверх задания (150:15 = 10).

Эффективным средством поиска различных способов решения для некоторых задач является выполнение удачной наглядной интерпретации задачи. Например, дана задача: «Длина огорода прямоугольной формы — 40 м, а ширина в 2 раза меньше. % площади огорода занято овощами, остальная площадь занята картофелем. Сколько квадратных метров занято картофелем?»

В процессе анализа текста задачи и ее решения рассуждения могут быть такими: «Длина огорода — 40 м, ширина — в 2 раза меньше, значит, можно найти ширину огорода: 40:2 = 20 (м). Известно: длина — 40 м, ширина — 20 м. Можно найти площадь участка: 40-20 = 800 (м²). Найдем площадь, занятую овощами: 800:4-3=600 (м²). Остальная часть занята картофелем — 200 м².»

Если построить к данной задаче схематический чертеж, то можно найти другие способы ее решения.

Чтобы найти площадь, занятую картофелем (рис. 1, а, б, в), достаточно найти длину и ширину участка, отведенного под картофель. Такие рассуждения доступны учащимся, и они могут самостоятельно найти решение по данной интерпретации задачи. Затруднения могут возникнуть при поиске решения по рис. 4, г. В этом случае учитель помогает учащимся осознать, что треугольники равны по площади и решение задачи будет иметь вид:

1) 40 – 20 = 800 (м²);

2) 800:4 = 200 (м²)

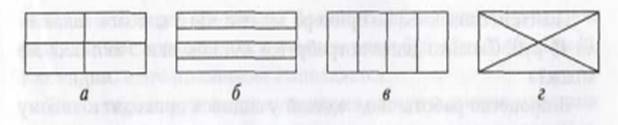
Рис. 2. Участки

Разработанная методика для слабослышащих детей отличается от методики преподавания текстовых задач для детей без ограничения здоровья использованием различных методов: наглядных, практических, словесных, игровых. Предложенные задачи влекут положительные изменения в отношении воспитанников к текстовым задачам; у обучающихся, воспитанников с нарушением слуха обогащается лексико-фразеологический запас, развивается умение грамматически правильно строить высказывания, а также развивается логическое мышление.