Методы решения задач на смеси, сплавы и концентрацию

Методы решения задач на смеси и сплавы.

Текстовые задачи входят в базовую часть ГИА. Кроме того, решение задач способствует развитию логического мышления, сообразительности и наблюдательности, умения самостоятельно осуществлять небольшие исследования. Задачи на смеси и сплавы при первом знакомстве с ними вызывают у учащихся общеобразовательных классов затруднения. Самостоятельно справиться с ними могут немногие.

При решении задач на смеси, сплавы и растворы следует иметь в виду, что к задачам по химии данные задачи отношения не имеют. В них не происходит химических реакций, вещества не испаряются, не переходят друг в друга.

При решении задач о смесях, сплавах, растворах используют следующие допущения:

1) все полученные смеси, сплавы, растворы считаются однородными;

2) не делается различия между литром как мерой вместимости сосуда и литром как мерой количества жидкости (или газа);

3) смешивание различных растворов происходит мгновенно;

4) объем смеси равен сумме объемов смешиваемых растворов;

5) объемы растворов и массы сплавов не могут быть отрицательными.

Задачи на смеси (сплавы) можно разделить на два вида:

1.Задаются, например, две смеси (сплава) с массами m₁ и m₂ и с концентрациями в них некоторого вещества. Смеси (сплавы) сливают (сплавляют). Требуется определить массу этого вещества в новой смеси (сплаве) и его новую концентрацию.

2.Задается некоторый объем смеси (сплава) и от этого объема начинают отливать (убирать) определенное количество смеси (сплава), а затем доливать (добавлять) такое же или другое количество смеси (сплава) с такой же концентрацией данного вещества или с другой концентрацией. Эта операция проводится несколько раз.

Задачи на смешивание растворов решают с помощью составления уравнения или системы уравнений. Главное внимание при обучении учащихся способу решения текстовых задач

методом составления уравнений должно быть обращено на сознательную отработку этапности решения

В процессе решения каждой такой задачи целесообразно действовать по следующей схеме.

1. Изучение условия задачи. Выбор неизвестных величин (их обозначаем буквами х, у и т.д.), относительно которых составляем пропорции. Выбирая неизвестные параметры, мы создаем математическую модель ситуации, описанной в условии задачи.

2. Поиск плана решения. Используя условия задачи, определяем все взаимосвязи между данными величинами.

3. Осуществление плана, т.е. оформление найденного решения – переход от словесной формулировки к составлению математической модели.

4. Изучение полученного решения, критический анализ результата.

Графический метод (составление рисунка).

1)                 Смешали 4 литра 15–процентного водного раствора некоторого вещества с 6 литрами 25–процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?  2. 2.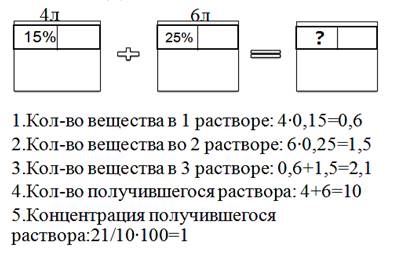

2)                 Имеется 2 сплава золота и серебра, в одном количество этих металлов находится в отношении 2:3, а в другом – в отношении 3:7. Сколько нужно взять каждого сплава, чтобы получить 8 кг нового сплава, в котором золото и серебро были в отношении 5:11?

 Решая любое из уравнений получаем   1 сплав -1кг, 2 сплав -7 кг

3)                 В 500 кг руды содержится некоторое количество железа. После удаления из руды 200 кг примесей, содержащих в среднем 12,5 % железа, содержание железа в оставшейся руде повысилось на 20 %. Определите, какое количество железа осталось ещё в руде?

 =  +          Х = 212,5 кг     212,5 -25 = 187,5 кг железа осталось в руде

4)                 Виноград содержит 90% влаги, а изюм – 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма? 

0,1Х =19      Х=  190 кг винограда нужно    Ответ: 19 кг.

5. Бронза – сплав меди и олова. В древности из бронзы отливали колокола, если в ней содержалось 75% меди. К куску бронзы 500кг и содержащему 72% добавили некоторое количество бронзы, содержащей 80% меди и получили бронзу, необходимую для изготовления колокола. Определите сколько добавили 80% бронзы.

Решение с помощью таблицы.

Получаем урвнение 0,75х (500+Х) =  360 +0,8Х,        375  - 360 = 0,05 Х,       Х = 300

Ответ:300кг.

6. Для приготовления смеси из двух жидкостей А и В было взято 16 литров жидкости А и разлито в два сосуда объемом по 16 литров каждый. Затем первый сосуд был долит жидкостью В и произведено перемешивание. Полученной смесью был дополнен сверху второй сосуд. Если отлить из второго сосуда в первый 8 литров получившийся смеси, то в первом сосуде будет жидкости А на три литра больше, чем во втором. Сколько всего использовано жидкости В для приготовления смеси?

Решение.

1 сосуд   х – жидкость А и (16-х) -  жидкость В     - доля жидкости А,

    - доля В

2 сосуд: первоначально в нём (16-х) жидкости А. Смесью из первого сосуда заполнили второй сосуд, так как в нём имеется (16-х) жидкости А, следовательно, дополнительно можно добавить только х литров смеси из первого сосуда. При этом во второй сосуд добавляется х∙  жидкости А и

х∙ жидкости В, таким образом во втором сосуде

 жидкости А стало   + (16-х) и  х∙ жидкости В.

Доля жидкости А во втором сосуде (  + (16-х) ): 16, доля жидкости В во втором сосуде х∙

Отлили из второго сосуда в первый 8 литров получившийся смеси, следовательно в первый сосуд поступило 8∙  жидкости А , в результате  стало в первом сосуде

(Х -  ) +  . В первом сосуде будет жидкости А на три литра больше, чем во втором, во втором осталось  8∙  жидкости А(в сосуде всего 16 литров жидкости, отлив 8 литров в сосуде остаётся 8л). Следовательно (Х -  ) = 3. Решаем уравнение получаем жидкость А составляет в первом сосуде 4 или 12 литров, следовательно жидкости В для приготовления смеси использовали 12л или 4л.

Ответ: 4литра, если в первый сосуд первоначально налили 12 литров жидкости А; 12 литров, если в первый сосуд первоначально налили 4 литра жидкости А.

ЗАДАЧИ из открытого банка ФИПИ

1.      В лаборатории изготовили 1кг 16% солевого раствора. Через неделю из этого раствора испарилось 200г воды. Какова стала концентрация соли в растворе?

Ответ:20%.

2.              При выплавке стали из чугуна, выжигается углерод. Содержание углерода в чугуне 4%. Сколько тонн углерода нужно выжечь из 245т чугуна, чтобы получилась сталь с содержанием углерода 2%?

Ответ:5т.

3.              Имеется 600г сплава золота и серебра содержащего золото и серебро в отношении 1:5 соответственно. Сколько грамм золота необходимо добавить к этому сплаву чтобы получить новый сплав содержащий 50% серебра.

Ответ:400г.

4.               Слиток сплава меди и цинка массой 36 кг содержит 45% меди. Какую массу меди надо добавить к этому куску, чтобы полученный сплав содержал 60% меди?

Ответ:13,5кг.

5.              После смешивания двух растворов, один из которых содержал 48 г, а другой — 20 г безводного йодистого калия, получилось 200 г нового раствора. Найдите концентрацию каждого из первоначальных растворов, если концентрация первого на 15% больше концентрации второго.

Ответ:40% и 25%.

6.              Имелось два слитка меди. Процент содержания меди в первом слитке на 40% меньше, чем во втором. После того как оба слитка сплавили, получился слиток, содержащий 36% меди. Найдите процентное содержание меди в каждом слитке, если в первом было 6 кг меди, а во втором — 12 кг.

Ответ:20% и 60%

8. Сколько чистого спирта нужно добавить к 735 г 16%-ного раствора йода и спирта, чтобы получить 10%-ный раствор?

Ответ:441г.

9. Смешали 30%-ный раствор соляной кислоты с ее 10%-ным раствором и получили 600 г 15%-ного раствора. Сколько граммов 30 % -ного раствора было взято?

Ответ:150г.

10. В сосуде находится 10%-ный раствор спирта. Из сосуда отлили 1/3 содержимого, а оставшуюся часть долили водой так, что сосуд оказался заполненным на 5/6 первоначального объема. Какое процентное содержание спирта оказалось в сосуде?

Ответ:8%.

11.              Имеются два слитка, состоящие из цинка, меди и олова. Известно, что первый слиток массой 150 кг содержит 40% олова, а второй массой 250 кг — 26% меди. Процентное содержание цинка в обоих слитках одинаково. Сплавив первый и второй слитки, получили сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в полученном сплаве?

Ответ:170 кг.

12.                             Имеются два сплава, состоящие из меди, цинка и олова. Известно, что первый сплав содержит 25% цинка, а второй — 50% меди. Процентное содержание олова в первом сплаве в 2 раза меньше, чем во втором. Сплавив 200 кг первого сплава и 300 кг второго, получили новый сплав, в котором оказалось 28% цинка. Определите, сколько килограммов меди содержится в получившемся новом сплаве.

Ответ: 280 кг.

13.                      Из сосуда, содержащего чистый спирт, отлили 20% содержимого и добавили такое же количество воды. Затем снова отлили 20% содержимого и добавили такое же количество воды. Какое минимальное количество раз надо повторить этот процесс, чтобы содержание спирта в сосуде стало меньше 30%?

     Ответ:6 раз.

14. Сплав весит 2 кг и состоит из серебра и меди, причем вес серебра составляет 14%   веса меди. Сколько серебра в данном сплаве?

Ответ:0,25 кг.

15. Имелись два разных сплава меди, причем процент содержания меди в первом сплаве был на 40% меньше, чем во втором. После того как их сплавили вместе, получили сплав, содержащий 36% меди. Определите процентное содержание меди в обоих сплавах, если известно, что в первом ее 6 кг, а во втором — вдвое больше.

Ответ:20% и 60%.

16.                         Два раствора, первый из которых содержал 800 г, а второй 600 г безводной серной кислоты, смешали и получили 10 кг нового раствора серной кислоты. Определите массу первого и второго растворов, вошедших в смесь, если известно, что процент содержания безводной серной кислоты в первом растворе на 10% больше, чем во втором.

Ответ:4кг и 6 кг.

17.            Морская вода содержит 5% (по весу) соли. Сколько килограммов пресной воды надо прибавить к 40 кг морской воды, чтобы содержание соли в последней составляло 2 %?

Ответ: 60 кг.

18.                             Имеется стальной лом двух сортов с содержанием никеля 5% и 40%. Сколько нужно взять металла каждого из этих сортов, чтобы получить 140 т стали с содержанием 30% никеля?

Ответ:40т и 100т.

19.                             Свежие грибы по весу содержат 90% воды, а сухие 12% воды. Сколько получится сухих грибов из 22 кг свежих?

Ответ:2,5 кг

20. Имеется сплав серебра с медью. Вычислите вес и пробу этого сплава, если его сплав с 3 кг чистого серебра есть сплав 900-й пробы, а его сплав с 2 кг сплава 900-й пробы есть сплав 840 пробы. (Проба благородного металла, равная например, 760 означает, что масса этого благородного металла в сплаве составляет 0,760 от массы всего сплава.)

Ответ: Вес первоначального сплава 3кг его проба 0,8.

21. Имеются три слитка. Первый весит 5 кг, второй 3 кг и каждый из этих слитков содержит 30% меди. Если первый слиток сплавить с третьим, то получится слиток, содержащий 56% меди, а если второй слиток сплавить с третьим, то получится слиток, содержащий 60% меди. Найдите вес третьего слитка и процент содержания меди в нем.

Ответ:10кг; 69%

22. Один сплав меди с оловом содержит эти металлы в отно­шении 2:3, другой — в отношении 3 : 7. В каком количестве надо взять эти сплавы, чтобы получить 12 кг нового сплава, в котором медь и олово были бы в отношении 3:5?

Ответ: 9кг и 3кг.

23. 40% раствор серной кислоты разбавили 60% раствором, после чего добавили 5кг воды и получили раствор 20% концентрации. Если бы вместо 5кг воды добавили 5 кг 80% раствора серной кислоты, то получился бы 70% раствор. Сколько было 40% и 60% раствора серной кислоты?

Ответ: 1кг  40% и 2кг  60%.