Недосказанные факты геометрии

Текст выступления.

Работа касается не то, чтобы мало исследованной, а совершенно неисследованной области: треугольников, чьи углы составляют геометрическую прогрессию. Почему такие треугольники с такими неожиданными, интересными и захватывающими свойствами, оказались в тени, пусть выясняют историки математики, а мы вернемся к работе, которая поражает широтой охватываемого материала.

В курсе геометрии мы изучаем понятие треугольник. Простейший из многоугольников–треугольник–играет в геометрии особую роль. Такова уже природа избранного треугольника с углами, составляющими геометрическую прогрессию, что его своеобразие и свойства хорошо высвечиваются именно н сопоставлении с другими типами треугольников и другими типами геометрических объектов. Исследуемый треугольник так богат свойствами, что их невозможно не только не исследовать, но и доказать в силу их полезности для расширения и углубления раздела геометрии «Треугольники»

Предмет исследования- свойства треугольников с углами и.

Цель работы: найти, исследовать и доказать свойства треугольника, углы которых составляют геометрическую прогрессию.

В этом и состоит новизна проекта: если о треугольниках, стороны которых составляют арифметическую прогрессию еще можно отыскать информацию, то о треугольниках, углы которых составляли бы геометрическую прогрессию, систематических исследований не проводилось. Между тем, свойства такого рода треугольников богаты, глубоки и интересны.

Гипотеза: существует треугольник, углы которого составляют геометрическую прогрессию обладающей отличительными, неизученными свойствами.

Значимость работы может быть рассмотрена в двух аспектах: а) научном, б) практическом.

Так как в работе доказаны свойства нового объекта, а именно треугольника, углы которого составляют геометрическую прогрессию, то работа имеет научное значение.

Работа относится к внутренним областям математики и прямого выхода в практику не имеет, а выходит в нее опосредствованно, через другие разделы математики. Проект будет интересен и доступен учащимся, заинтересованным в расширении и углублении знаний в области геометрии. Материал работы может быть использован в математических классах, кружках и факультативах в качестве пособия для ознакомления с особыми типами треугольников и их свойствами. Окажется он полезным и для самих учителей.

Треугольники, углы которых составляют геометрическую прогрессию

Треугольники, углы которых составляют геометрическую прогрессию это треугольники с углами и.Эти треугольники отличаются большим набором интересных свойств, нахождением и доказательством которых мы будем заниматься в нашем проекте.

Новые свойства треугольников, углы которых составляют геометрическую прогрессию

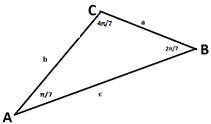Теорема 1. Сумма квадратов сторон треугольника углы которого равны и равна 7, где R есть радиус описанной окружности данного треугольника.

Доказательство.

Пусть имеется треугольник АВС с указанными свойствами:         ∠A = , ∠B = ,   ∠C =  и сторонами, равными а. b. с. (рис. 1).Тогда по теореме синусов (Теорема, устанавливающая зависимость между длинами сторон треугольника и величиной противолежащих им углов. Существуют два варианта теоремы; обычная теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.и расширенная теорема синусов для произвольного треугольника,где a {\displaystyle a},b {\displaystyle b},c {\displaystyle c} — стороны треугольника, ∠A,B,C{\displaystyle \alpha ,\beta ,\gamma } — соответственно противолежащие им углы, а {\displaystyle R}R — радиус окружности, описанной около треугольника:  и

Отсюда получим:  или используя формулу двойного угла синуса

sin(2α) = 2sin(α)cos(α) получаем =  .Тогда длина стороны а может быть выражена следующим равенством

a= из которого выразим в : в = 2а * cos.

Аналогично выразим длину стороны с через в:  ;  =    ;

b=  из которого окончательно выразим длину с через b: c = 2b * cos.

Для рассмотрения выражения длины стороны а через с нам понадобится формула приведения тригонометрии:sin= sin(π-)= sin () и получаем 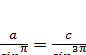. Аналогично

sinsin ( π-)=sin=2 sincos., тогда  = 

Получаем, что длина стороны а может быть выражена следующим равенством

a= из которого выразим в : в = 2а * cos.

Сложим теперь все три равенства, предварительно возведя каждое в квадрат, получим

a²+ b²+c²=4a²+4b²+4c².С другой стороны:a²=4R², b²=4R²,c²=4R². Откуда окончательно

a²+ b²+c²=4a²+4b²+4c²=4R²

=4R²(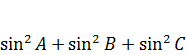)=4R²(2+2cosA•cosB•cosC)=4R²• =7R².

Что и требовалось доказать.

Теорема 2: Если a, b, c стороны треугольника АВС с угламии, то сторона а равна половине среднего гармонического двух других его сторон. 

Используя это утверждение можно показать, что b=, c=

Теорема 3: Еслиh_a, h_b, h_c   - высоты, опущенные соответственно на стороны а,b,c треугольника АВС с углами   ∠A= ∠B= ,      ∠C= , то h_a1=h_b + h_c

Теорема 4:Суммы квадратов высот треугольника АВС с угламииравны половине суммы квадратов его сторон:h_a²+ h_b²+ h_c²=

Скачано с www.znanio.ru