Описание опыта использования на уроках физики электронных образовательных ресурсов

Практическая работа 3 (2 ч.). Описание опыта использования на уроках физики электронных образовательных ресурсов.

Цель: освоение технологий применения цифровых образовательных ресурсов на уроках физики.

Задание 1. Опишите технологию использования одного цифрового образовательного ресурса или электронной образовательной площадки в учебном процессе.

Практическая работа должна быть выполнена на листах формата А4.

Оформление каждого нового структурного элемента работы начинается с новой страницы. Страницы практической работы должны быть пронумерованы.

Объем выполненной работы – не менее 2 страниц.

Критерии оценки:

- степень реализации цели практической работы;

- степень выполнения заданий работы;

- степень сформированности у слушателей необходимых знаний и умений;

Оценка: зачет/незачет.

Задание 1.

Задание «Исторические сведения»

Цель: формирование умения оценивать факты, события, явления и процессы с помощью разных критериев, выделять причинно-следственные связи.

Возраст: 17 — 18 лет.

Учебные дисциплины: математика и физика.

Форма учебно-познавательной деятельности: работа индивидуальная и в группах по 4—5 человек.

Описание задания: учащимся предлагается провести теоретическое исследование. Теоретическое исследование – это формулирование общих закономерностей, позволяющих объяснить ранее открытые факты и эмпирические закономерности.

Этапы проведения исследования

1. Формулирование проблемы.

2. Подготовка к проведению исследования:

- предварительный анализ имеющейся информации, выдвижение гипотез;

- отбор материала, который будет использован в исследовании.

3. Проведение исследования:

- анализ и обобщение результатов исследования.

4. Изложение результатов исследования, их представление.

5. Обсуждение, оценка полученных результатов.

Материал: текст на карточке.

Текст.

Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:

·                     о разыскании касательной к произвольной линии;

·                     о разыскании скорости при произвольном законе движения.

Еще раньше понятие производной встречалось в работах итальянского математика Николо Тартальи (около 1500 – 1557гг.) – здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.

В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной.

Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л.Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.

Мгновенная скорость о разыскании скорости при произвольном законе движения.

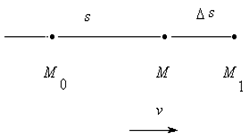
Пусть точка M движется по прямой. Расстояние s движущейся точки, отсчитываемое от некоторого начального ее положения M₀ , зависит от времени t , т.е. s есть функция времени t: s = f(t). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M₀, а в некоторый следующий момент t + ∆t оказалась в положении M₁ – на расстоянии s + ∆s от начального положения (см. фото) [3]. Таким образом, за промежуток времени ∆t расстояние s изменилось на величину ∆s. В этом случае говорят, что за промежуток времени ∆t величина s получила приращение ∆s

 (изменение «на»).

Отношение  представляет собой среднюю скорость движения точки за время ∆t:ν_ср = .

Средняя скорость не может во всех случаях точно охарактеризовать быстроту перемещения точки M в момент времени t. Если, например, тело в начале промежутка ∆t перемещалось очень быстро, а в конце очень медленно, то средняя скорость не сможет отразить указанных особенностей движения точки и дать представление об истинной скорости ее движения в момент t. Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени ∆t. Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при ∆t → 0, как бесконечно малая величина. Этот предел называют скоростью движения в данный момент:

ν = .

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути ∆s к приращению времени ∆t, когда приращение времени стремится к нулю. Так как ∆S = f (t + ∆t) – f(t),

то ν = .

 В жизни, мгновенной скоростью движения автомобиля, является скорость на спидометре в данный момент времени.

Вопросы:

1. Назовите имена учёных, которые участвовали в создании производной. Что их к этому подвигло?

2.Почему в физике существует необходимость говорить о мгновенной путевой скорости?

3. Автомобиль едет по закруглённому участку дороги, обладает ли он мгновенной скоростью? Почему?

4. Зная решение задачи о мгновенной скорости движения, предположите ключевые слова к понятию «производной».

Для того, чтобы ответить на вопросы, учащимся нужно вспомнить (прочитать), что необходимо знать, чтобы понимать производную функции, описать движение тела по закруглённому участку дороги, сравнить две задачи о «разыскании» и определить общие слова к понятию «производной».

Примечание: задачу можно решать при создании на уроке математике проблемной ситуации (на уроке – изучение нового материала, работая в парах по 2 человека, как и,  при проведении обобщающего урока).

Учебные ресурсы.

1. [Электронный ресурс]. Код доступа http://www.cleverstudents.ru

2. [Электронный ресурс]. Код доступа http://www.krugosvet.ru/images/1012636_image008.gif

3.  [Электронный ресурс]. Код доступа http://cdn01.ru/files/users/images/23/2e/232e5e68f95eadc79dee88b42d47f7fe.jpg

4.  Методическое руководство для работы с цифровой лабораторией/ ООО ТД «Учебное Оборудование L-микро Россия». Москва 2021г.

Скачано с www.znanio.ru