Описание работы шифратора, таблица истинности, логическая схема

Описание работы шифратора, таблица истинности, логическая схема

Шифратор — это комбинационное устройство, преобразующее десятичные числа в двоичную систему счисления, причем каждому входу может быть поставлено в соответствие десятичное число, а набор выходных логических сигналов соответствует определенному двоичному коду. Шифратор иногда называют «кодером» (от англ. coder) и используют, например, для перевода десятичных чисел, набранных на клавиатуре кнопочного пульта управления, в двоичные числа. Если количество входов настолько велико, что в шифраторе используются все возможные комбинации сигналов на выходе, то такой шифратор называется полным, если не все, то неполным. Число входов и выходов в полном шифраторе связано соотношением n= 2m, где n— число входов, m— число выходов. Так, для преобразования кода кнопочного пульта в четырехразрядное двоичное число достаточно использовать лишь 10 входов, в то время как полное число возможных входов будет равно 16 (n = 24 = 16), поэтому шифратор 10×4 (из 10 в 4) будет неполным. Рассмотрим пример построения шифратора для преобразования десятиразрядного единичного кода (десятичных чисел от 0 до 9) в двоичный код. При этом предполагается, что сигнал, соответствующий логической единице, в каждый момент времени подается только на один вход. Условное обозначение такого шифратора и таблица соответствия кода приведены на (рисунке 1)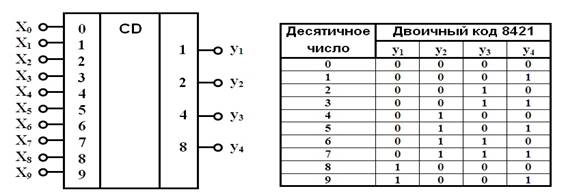   

Рисунок 1

Используя данную таблицу соответствия, запишем логические выражения, включая в логическую сумму те входные переменные, которые соответствуют единице некоторой выходной пере­менной. Так, на выходе у1 будет логическая «1» тогда, когда логическая «1» будет или на входе Х1,или Х3, или Х5, или Х7, или X9, т. е. у1 = Х1+ Х3+ Х5+ Х7+X9 Аналогично получаем у2 = Х2 + Х3 + Х6 + X7 у3 = Х4 + Х5 + Х6 + Х7 у4 = Х8 + X9 Представим на (рисунке 2) схему такого шифратора, используя элементы ИЛИ.

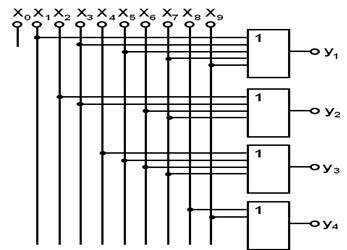
Рисунок 2

Таблица истинности - таблица, описывающая логическую функцию. Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность.

На практике часто используют шифратор с приоритетом. В таких шифраторах код двоичного числа соответствует наивысшему номеру входа, на который подан сигнал «1», т. е. на приоритетный шифратор допускается подавать сигналы на несколько входов, а он выставляет на выходе код числа, соответствующего старшему входу.
    Рассмотрим в качестве примера (рисунок 3) шифратор с приоритетом (приоритетный шифратор) К555ИВЗ серии микросхем К555 (ТТЛШ).

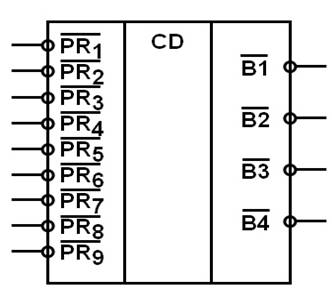
Рисунок 3

Шифратор имеет 9 инверсных входов, обозначенных через PRl, …, PR9 . Аббревиатура PR обозначает «приоритет». Шифратор имеет четыре инверсных выхода Bl, …, B8 . Аббревиатура B означает «шина» (от англ. bus). Цифры определяют значение активного уровня (нуля) в соответствующем разряде двоичного числа. Например, B8 обозначает, что ноль на этом выходе соответствует числу 8. Очевидно, что это неполный шифратор.

Если на всех входах — логическая единица, то на всех выходах также логическая единица, что соответствует числу 0 в так называемом инверсном коде (1111). Если хотя бы на одном входе имеется логический ноль, то состояние выходных сигналов определяется наибольшим номером входа, на котором имеется логический ноль, и не зависит от сигналов на входах, имеющих меньший номер.

Например, если на входе PR1 — логический ноль, а на всех остальных входах — логическая единица, то на выходах имеются следующие сигналы: В1 − 0, В2 − 1, В4 − 1, В8 − 1, что соответствует числу 1 в инверсном коде (1110).

Если на входе PR9 логический ноль, то независимо от других входных сигналов на выходах имеются следующие сигналы: В1 − 0 , В2 − 1 , В4 − 1, В8 − 0, что соответствует числу 9 в инверсном коде (0110).

2.1.2.Таблица истинности — таблица, описывающая логическую функцию.

Под логической функцией в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения истина либо ложь(рисунок 4).

Рисунок  4- Примеры таблицы истинности логических функций