Опорный конспект по геометрии по теме «Осевая и центральная симметрия» (8 класс)

Осевая и центральная симметрия

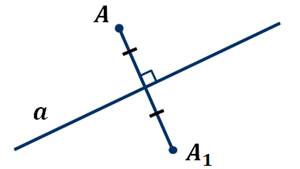
Точки  и называются симметричными относительно прямой , если эта прямая проходит через середину отрезка  и перпендикулярна отрезку .

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.

Прямую а называют осью симметрии фигуры.

Осевой симметрией обладает равнобедренный треугольник.

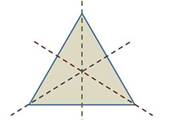
 Он имеет одну ось симметрии, на которой расположена биссектриса, проведённая из вершины к основанию. Равносторонний треугольник также обладает осевой симметрией и имеет три оси симметрии, на которых расположены биссектрисы углов треугольника.

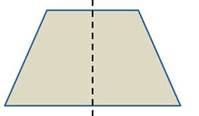
Равнобедренная трапеция имеет ось симметрии, на которой лежит прямая проходящая через середины её оснований.

Прямоугольник имеет две оси симметрии, которые проходят через середины его противолежащих сторон.

Ромб также имеет две оси симметрии, на которых расположены его диагонали…

Квадрат имеет четыре оси симметрии, так как одновременно является и прямоугольником и ромбом.

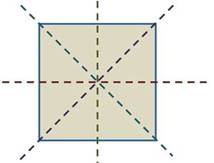
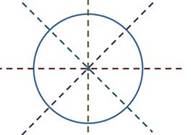
А вот у окружности каждая прямая, проходящая через её центр, является осью симметрии. Так как таких прямых можно провести бесконечно много, то и осей симметрии у окружности бесконечно много.

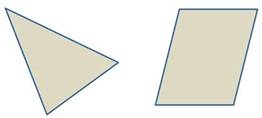
Но есть и фигуры, у которых нет ни одной оси симметрии. Примерами таких фигур являются разносторонний треугольник. Или параллелограмм, который не является прямоугольником или ромбом.

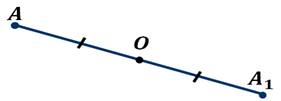
Точки А и A₁ называются симметричными относительно точки О, если точка О – середина отрезка АА₁.

 Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.

Точку О называют центром симметрии фигуры.

Центральной симметрией обладает окружность.

Её центр является центром симметрии.

Параллелограмм также обладает центральной симметрией. Центром его симметрии является точка пересечения диагоналей.

Прямоугольник, ромб и квадрат также обладают центральной симметрией, центром которой является точка пересечения их диагоналей.

Центральной симметрией обладает и прямая, причём любая точка прямой является центром её симметрии.

Примером фигуры, не обладающей центральной симметрией, является произвольный треугольник.

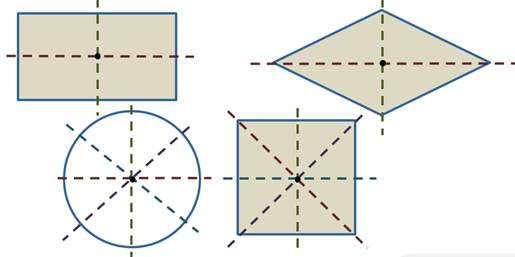
А вот, например, такие фигуры, как прямоугольник, ромб, квадрат, окружность имеют обе симметрии (осевую и центральную).