Открытый урок алгебры в 10 классе на тему "Логарифмические неравенства"

Муниципальное бюджетное образовательное учреждение

«Школа № 78 города Донецка»

 

 

 

 

 

 

 

 

 

 

 

 

Открытый урок алгебры и начала математического анализа

в 10 классе на тему:

«Логарифмические неравенства»

 

 

 

 

 

 

 

 

Составитель:

Крыжановская Яна Викторовна,

учитель математика МБОУ «Школа №78 г.Донецка»

 

 

 

 

 

 

 

 

 

 

 

Донецк, 2023

Предмет: Алгебра и начала математического анализа

Класс: 10-Б                                                                        Дата: 03.02.2023

 

Учебник: Математика: алгебра и начала математического анализа, геометри. Алгебра и начала математического анализа, 10-11 классы: учеб.для общеобразоват. Организаций; базовый и углуб.уровни/[Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева и др.] – 5-е изд. – М.: Просвещение, 2022г. – 463с., ил.

 

Тип урока: урок применения знаний на практике.

 

Форма урока: урок-практикум.

 

Формы организации учебной деятельности: фронтальная, индивидуальная, групповая, парная.

 

Техническое обеспечение: классная доска, компьютер, проектор, экран, презентация, карточки с заданиями для работы всех обучающихся.

 

Методы обучения: репродуктивный, частично-поисковый, объяснительно-иллюстративный, проблемно-поисковый, творческий.

 

Система контроля на уроке: сочетание самоконтроля и контроля учителя.

 

Тема урока: «Логарифмические неравенства»

 

Цели урока:

 

Образовательные:

-       определение и свойства логарифма, логарифмической функции; способы решения логарифмических неравенств.

Развивающие:

-       формирование практических навыков решения логарифмических неравенств на основе изученного теоретического материала;

-       закрепление навыков решения логарифмических неравенств из заданий ЕГЭ: №5, №7,№17 базового уровня и № 9, № 10, №17 – профильного уровня;

-       развитие умений нахождения рационального способа решения;

-       формирование УУД.

 

Воспитательные:

-       воспитание уверенности, ответственности, познавательного интереса к обучению.

 

Задачи урока:

-       научить оперировать имеющимся потенциалом знаний по теме «Логарифмические уравнения и неравенства» в конкретной ситуации;

-       закрепить основные методы решения логарифмических уравнений и неравенств, предупредить появление типичных ошибок, подготовить к итоговой аттестации;

-       предоставить каждому обучающемуся возможность проверить свои знания и повысить их уровень;

-       вовлечь учащихся в активную практическую деятельность;

-       воспитывать у обучающихся чувство ответственности, уверенности в себе;

-       использовать на уроке здоровье сберегающие средства обучения математике так, чтобы учащиеся смогли включиться в работу в соответствии с индивидуальными возможностями;

-       обеспечить оптимальное соотношение между физическим и информационным объемом урока без информационной перегрузки учащихся

 

Планируемые результаты:

Предметные умения:

Знание различных методов решения логарифмических неравенств:

-       сведение неравенств к равносильной системе или совокупности систем;

-       расщепление неравенств;

-       метод интервалов;

-       введение новой переменной;

-       метод рационализации.

Личностные УУД:

-       определять правила работы в группах, парах:

-       оценивать усваиваемое содержание (исходя из личностных ценностей);

-       устанавливать связь между целью деятельности и ее результатом.

 

Регулятивные УУД:

-       определять и формулировать цель деятельности на уроке;

-       проговаривать последовательность действия на уроке;

-       работать по плану, инструкции;

-       высказывать свое предположение на основе учебного материала;

-       осуществлять самоконтроль и взаимоконтроль;

-       уметь самостоятельно контролировать свое время и управлять им.

Познавательные УУД:

-       находить ответы на вопросы поставленные учителем;

-       проводить анализ учебного материала;

-       проводить сравнение, классификацию, указывая на основание классификации;

-       создавать и преобразовывать модели и схемы для решения задач.

Коммуникативные УУД:

-       слушать и понимать речь других;

-       уметь с достаточной полнотой и точностью выражать свои мысли;

-       владеть монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка.

 

 

Ход урока

 

1.     Организационный момент

Дидактическая цель: создание благоприятной психологической атмосферы, настрой на совместную работу.

 

Учитель: Дорогие ребята и уважаемые гости! Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех присутствующих. Очень хочу, чтобы с нашего урока все ушли с глубоким убеждением: математика - интересный предмет. Проверьте, пожалуйста, все ли готовы к работе: все ли принадлежности находятся на столах.

- Девизом урока я выбрала слова писателя Бориса Васильева:

«Мне необходимо разобраться самому, а чтобы разобраться самому, надо думать сообща».

 

2.     Мотивация к учебной деятельности.

Дидактическая цель: активизация мыслительных операций и познавательных процессов.

Ребята, послушайте, какая тишина!

Это в школе начались уроки.

Мы не будем тратить время зря

И приступим все к работе.

Учитель: Математика - наука трудная. Вы готовы преодолеть трудности на пути к знаниям? Тогда пожелайте друг другу удачи. Я желаю вам удачи!

У НАС ВСЁ ПОЛУЧИТСЯ!

Сегодня на уроке у нас присутствуют гости. Мы должны показать знания, полученные при изучении данной темы.

А вот как называется тема нашего урока, вы узнаете из устных заданий.

 

Учитель. Какие неравенства являются логарифмическими?

1)

2)

3) 2x+5≤ log5125

4)     ответ: 1,2,4.

(Слайд №1)

Учитель. А теперь назовите тему нашего урока (Логарифмические неравенства).

 

Учитель. Открываем  тетради, записываем число, классная работа, тема урока «Логарифмические неравенства».

(Слайд №2)

Учитель. Скажите ребята, а мы уже решали с вами логарифмические неравенства? (Да).

Тогда попробуйте сформулировать цель нашего урока? (Обобщить знания по решению логарифмических неравенств).

 (Слайд № 3)

 

Учитель: А где пригодятся знания по решению логарифмических неравенств? (При сдаче  ЕГЭ).

 

Учитель. Какой теоретический материал будет вам необходим при решении логарифмических неравенств? (Чтобы решить логарифмические неравенства,  нужно знать определение и свойства логарифма, свойства логарифмической функции, определение логарифмического неравенства, алгоритм решения логарифмического неравенства).

 

3.     Устный опрос.

 

Учитель. Сформулируйте определение логарифма?

(«Логарифмом числа b  по основанию a, где a > 0, a ≠ 1, называется показатель  степени, в которую нужно возвести число a, чтобы получить число b:

log _a b = x            a^x = b при a>0, a≠1, b>0»).

(Слайд 4)

Учитель: Назовите формулы и свойства логарифмов, которые мы используем при решении логарифмических неравенств? Поставьте в соответствие каждой формуле её вторую часть.

 

Ответы:1-6,2-3,3-5,4-4,5-2,6-1

(Слайд №5)

Учитель. При каком условии логарифмическая функция возрастает, убывает? (Если а>1,то у= log_ax-возрастает, если 0<а<1, то у= log_ax-убывает).

(Слайд 6)

Учитель. Какова область определения логарифмической функции?  (Для у= log_ax, х>0).

(Слайд 7)

Учитель. Какие неравенства называются логарифмическими?

(Логарифмическими неравенствами называются неравенства вида  

log_a f(x)≥ log_ag(x), где а>0,а≠1).

(Слайд 8)

Учитель. Сформулируйте алгоритм решения простейшего логарифмического неравенства.

1) Найти ОДЗ неравенства (подлогарифмическое выражение больше нуля).

2) Представить (если возможно) левую и правую части неравенства в виде логарифмов по одному и тому же основанию.

3) Определить, возрастающей или убывающей является логарифмическая функция: если а > 1, то возрастающая; если 0 < а < 1, то убывающая.

4) Перейти к более простому неравенству (подлогарифмических выражений), учитывая, что знак неравенства сохранится, если функция возрастает, и изменится, если она убывает.

5) Записать ответ с учётом ОДЗ.

(Слайд 9)

Учитель. Какие логарифмические неравенства требуют дополнительных знаний. (Часто, при решении логарифмических неравенств, встречаются неравенства с переменной в основании логарифма. Так, неравенство вида

является стандартным школьным неравенством.)

(Слайд 10)

Учитель. В чём заключается классический способ решения логарифмического неравенства

.

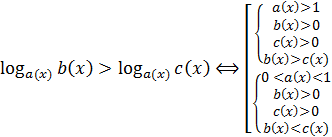(Слайд 11)

 

Учитель. С неравенства

.

Если существует, то как он называется?. (Существует. Это метод рационализации неравенств)

 (Слайд 12)

Учитель. В чём заключается метод рационализации? (Метод рационализации заключается в замене сложного выражения F(x) на более простое выражение G(x), при которой неравенство G(x)>0 равносильно неравенству F(x)>0 в области определения F(x).)

(Слайд 13)

Учитель. Формулы метода рационализации.

(Слайд 14)

(f, g, h– выражения с переменной х, a– фиксированное число или функция   ( а>0, a≠1).

 

	Выражение F	Выражение G
1
2
3
4
5
6

Учитель. Алгоритм решения неравенств

методом рационализации.

Шаг 1. ОДЗ: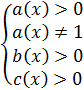   

Шаг 2. Преобразование логарифмического неравенства к виду:

Шаг 3. Метод рационализации:  (a(x)-1) · (b(x)-c(x))>0

Шаг 4. Запись ответа с учётом ОДЗ.

(Слайд 15)

 

Учитель: Ребята, у вас на столах справочный материал, который поможет вам при решении неравенств.

 

4.     Учебно-познавательная деятельность.

 

Задание № 1. Решите неравенство:

(Слайд №16)

Решение.

 

Рис.1 Решение первого неравенства задания №1

Рис.2 Решение второго неравенства задания №1.

 

Рис.3 Решение третьего неравенства задания №1

Рис.4 Решение четвертого неравенства задания №1.

 

Форма работы: Работают у доски и в тетрадях

 

Учитель:  Проверка на слайде.

(Слайд № 17-№ 20)

Задание № 2. Решите неравенство (работа у доски)

(Слайд №21)

 

Решение.

Рис.5 Решение первого неравенства задания №2

 

Рис.6 Решение второго неравенства задания №2

(Слайд №22-23)

5.     Релаксирующая деятельность.

 

Мы немного все устали. Давайте отдохнем.

Мы все вместе улыбнёмся,

Подмигнём слегка друг другу.

Вправо, влево повернёмся (повороты вправо, влево)

И кивнём затем по кругу (наклоны вправо, влево).

Все идеи победили,

Вверх взметнулись наши руки (поднимаем руки вверх),

Груз забот с себя стряхнули

И продолжим путь науки.

Физкультминутка. (Звезды)

(Слайд № 24)

 

Учитель: Решим задания типа № 15 ЕГЭ.

 

Задание №3. Решите неравенство

(Слайд № 25)

Решение у доски : 1 ученик решает классическим способом, 2 ученик- методом рационализации. На местах учащиеся решают одним из способов.

 

Решение.

Рис. 7 Решение неравенства классическим методом

Рис. 8 Решение неравенства методом рационализации

(Слайд № 26-№ 27)

 

Задание №4. Решите неравенство

(Слайд № 28)

Решение.

Рис. 9 Решение неравенства методом рационализации

 

Слайд № 29

Форма работы: Разбор задания выполняется у доски.

 

6.     Рефлексивная деятельность

Цель: оценить результат учебной деятельности.

 

Учитель: Давайте вернемся к цели нашего урока. Ребята, скажите, достигли мы цели сегодня на уроке?

 

1. А что мы повторили? (Решение логарифмических неравенств).

2. Где пригодится в жизни? (При сдаче ЕГЭ).

 

Ребята предлагаю вам последнее задание. Выберите то предложение, которое подходит для вас.

1) «В теме не разобрался, нуждаюсь в консультации».

2) «В теме не всё понятно, дома нужно хорошо поработать».

3) «В теме разобрался, домашнее задание выполню самостоятельно».

(Слайд № 31)

 

Учитель: Молодцы, каждый из вас показал хорошую работу, хочется пожелать вам ребята дальнейших успехов в изучении такого интересного предмета, как математика, а самое главное хорошо сдать ЕГЭ.

 

7.     Домашнее задание.

На карточках.

 

Вариант 1

1.Найдите произведение всех целых чисел, являющихся решением неравенства:

;⁡

2.Найдите наибольшее целое решение неравенства:

;

3.Решите неравенства:

а) ;

б)  >0.

 

Вариант 2

1.Найдите произведение всех целых чисел, являющихся решением неравенства:

;

 

2. Найдите наибольшее целое решение неравенства:

;

3. Решите неравенства:

а);

б)  >0.

(Слайд №15)

 

Работа оценивается для диагностики качества освоения темы.

 

 

 

 

Приложение