ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ

Относительная погрешность
приближённого значения

Цели: ввести понятие относительной погрешности приближённого значения; формировать умение оценивать качество измерения с помощью относительной погрешности.

Ход урока

I. Устная работа.

1. Приближённое значение числа х равна а. Найдите абсолютную погрешность приближения, если:

а) х = 2,85, а = 2,9;                    в) х = 18,65, а = 19;

б) х = 26,3, а = 26;                     г) х = 686, а = 690.

2. Оцените точное значение b, если:

а) b = 6 ± 1;                                в) b = 14,568 ± 0,001;

б) b = 15 ± 0,1;                           г) b = 120 ± 10.

При проведении устной работы одновременно актуализируем определение абсолютной погрешности приближённого значения.

II. Объяснение нового материала.

1. М о т и в а ц и я   и з у ч е н и я.

Предлагаем учащимся для рассмотрения следующую ситуацию. Марина, измеряя длину детали, имеющую истинную длину 10 см, допустила абсолютную погрешность, равную 1 см. Сергей, измеряя длину комнаты, истинная длина которой 5 м, также допустил абсолютную погрешность, равную 1 см. В о п р о с: кто из ребят выполнил измерение более точно (качественно)?

Учащиеся интуитивно понимают, что Сергей более качественно выполнил работу, так как относительно размера комнаты эта абсолютная погрешность не столь существенна, как относительно размера детали.

2. С о о б щ а е м   у ч е н и к а м,  что точность приближения или его качество, как правило, характеризуется не абсолютной его погрешностью, а относительной. Выносим на доску запись:

В рассмотренной выше ситуации при измерении (в сантиметрах) детали и длины комнаты получены результаты:

а = 10 ± 1 (длина детали);

b = 500 ± 1 (длина комнаты).

В  первом  случае  относительная  погрешность  составляет , во втором .  Выразив  относительную  погрешность  в  процентах,  получим 10 % и 0,2 %.

В ы в о д: чем меньше относительная погрешность приближения, тем приближение считается более точным.

3. Используя пример со с. 166–167 учебника, разбираем способ оценки относительной погрешности в случае, когда абсолютная погрешность не известна, а известна только точность приближённого значения.

Пусть а – приближённое значение х с точностью до h, тогда х = а ± h. Значит, относительная погрешность не превосходит  ∙  100 %. Иными словами, приближение выполнено с точностью до  ∙  100 %.

III. Формирование умений и навыков.

Все упражнения, которые учащиеся должны выполнить на этом уроке, можно разбить на  т р и   г р у п п ы:

1) Определение точности измерения.

2) Вычисление относительной погрешности приближённого значения по абсолютной погрешности.

3) Оценка относительной погрешности приближённого значения по его точности.

1. № 790, № 791.

Р е ш е н и е

№ 791.

17,9 мм – получено штангенциркулем;

18 мм – получено линейкой;

17,86 мм – получено микрометром.

И з м е р е н и е:

– линейкой с точность до 1 мм;

– штангенциркулем с точностью до 0,1 мм;

– микрометром с точностью до 0,01 мм.

2. Округлите число единиц и найдите относительную погрешность округления:

а) 1,7;          б) 5,314.

Р е ш е н и е

а) 1,7 ≈ 2.

Абсолютная погрешность равна | 1,7 – 2 | = 0,3.

Относительная погрешность равна ∙  100 % = 15 %.

б) 5,314 ≈ 5.

Абсолютная погрешность равна | 5,314 – 5 | = 0,314.

Относительная погрешность равна 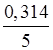∙  100 % = 6,28 %.

О т в е т: 15 %; б) 6,28 %.

3. № 793.

Р е ш е н и е

ρ = 7,8 г/см³ – табличное значение плотности железа.

7,6 г/см³ – приближённое значение.

Абсолютная погрешность составляет | 7,8 – 7,6 | = 0,2.

Относительная погрешность равна ∙  100 % ≈ 2,6 %.

О т в е т: ≈ 2,6 %.

4. № 795.

Р е ш е н и е

d = 0,15 ± 0,01 мм;

l = 384000 ± 500 км.

Относительная погрешность измерения толщины волоса не превышает ∙  100 %, то есть ≈ 6,7 %.

Относительная погрешность измерения расстояния от Земли до Луны не превышает 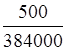 ∙  100 %, то есть 0,1 %.

6,7 % > 0,1 %, значит, измерение расстояния от Земли до Луны произведено более качественно (с большей точностью).

IV. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Почему по абсолютной погрешности приближённого значения нельзя судить о качестве приближения (измерения)? Приведите пример.

– Что называется относительной погрешностью приближённого значения?

– Каким образом можно оценить относительную погрешность приближённого значения, если абсолютная погрешность неизвестна?

Домашнее задание.

1. № 792, № 794.

2. Сравните качества измерения массы М электровоза и массы т таблетки лекарства, если М ≈ 184т (с точностью до 0,5т) и т ≈ 0,25 г (с точностью до 0,01 г).

3. Подготовка к контрольной работе, повторить п. 28–30.

№ 797 (а), № 930 (а), № 932.